Похожие презентации:
Операционное исчисление
1. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
I. Преобразование Лапласа2018
2. ОРИГИНАЛ
комплекснозначная функциядействительного переменного
f (t ) f1(t ) if 2 (t )
3.
ТЕОРЕМА 1S
t
0
f (t ) e
S0 - Показатель роста
4.
5.
6. Единичная функция Хевисайда
1L(1) L(η(t ))
p
7.
8. Пример1
Найти изображение по определениюe
2t
9. Пример 1
10. Основные свойства
11.
12.
13.
14.
15.
16.
17.
18.
19. Примеры
20.
21.
22.
23.
24.
25. II. Отыскание оригинала по изображению
1. Теорема запаздывания2. Теорема о свертке
3. Изображение – правильная дробь, вида
Qm ( p )
Rn ( p )
1. Разложить в сумму простейших дробей изображение
2. Перейти к оригиналам от полученных дробей
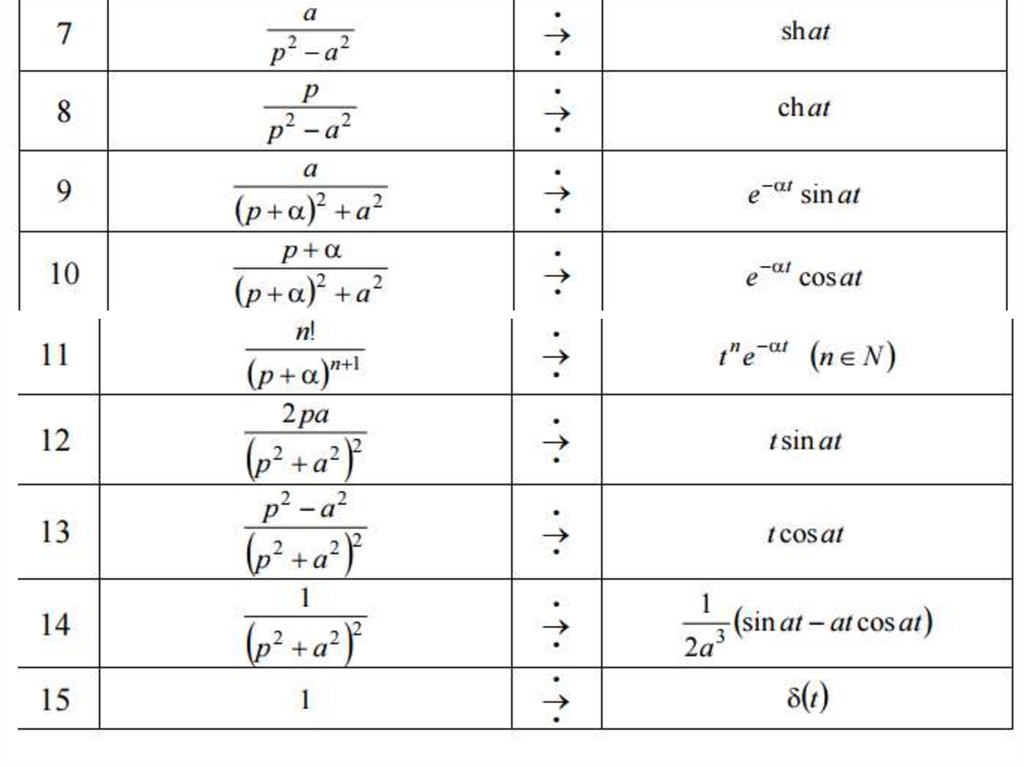
26. Оригиналы простейших дробей
27. Оригиналы простейших дробей
28. Пример
3p 4
2
( p 1)3
4
( p 2) 6
29.
p 12
p 4p 5
30.
p 1p2 4 p 5
31. Применение операционного исчисления
1. Вычисление несобственных интегралов2. Решение линейных дифференциальных
уравнений с постоянными
коэффициентами
3. Решение систем линейных
дифференциальных уравнений
32. Пример
sin tt dt
0
Пример
33. ЛДУ
Найти решение ДУ операторным методом при заданныхначальных условиях
a0 y a1 y a2 y f (t ),
y (0) y0 , y (0) y0
34. 2. Алгоритм решения ЛДУ
1. Применить преобразование Лапласа к правойчасти по таблице изображений
2. Найти изображение левой части, используя
дифференцирование оригинала (свойство 5)
3. Получаем операторное уравнение относительно
Y(p) – изображение решения ДУ
4. Выразить Y(p)
5. Восстановить оригинал y(t) по полученному
изображению
35. Пример
ty 2 y y e , y(0) 1, y (0) 0
36. Пример
37. Пример
38.
39. 3. Алгоритм решения систем ДУ
1. Применить преобразование Лапласа кобеим частям каждого уравнения
2. Решить полученную систему, как СЛАУ
относительно
изображений
искомых
решений (метод Крамера)
3. Восстановить оригиналы – решения
системы ДУ по полученным изображениям



























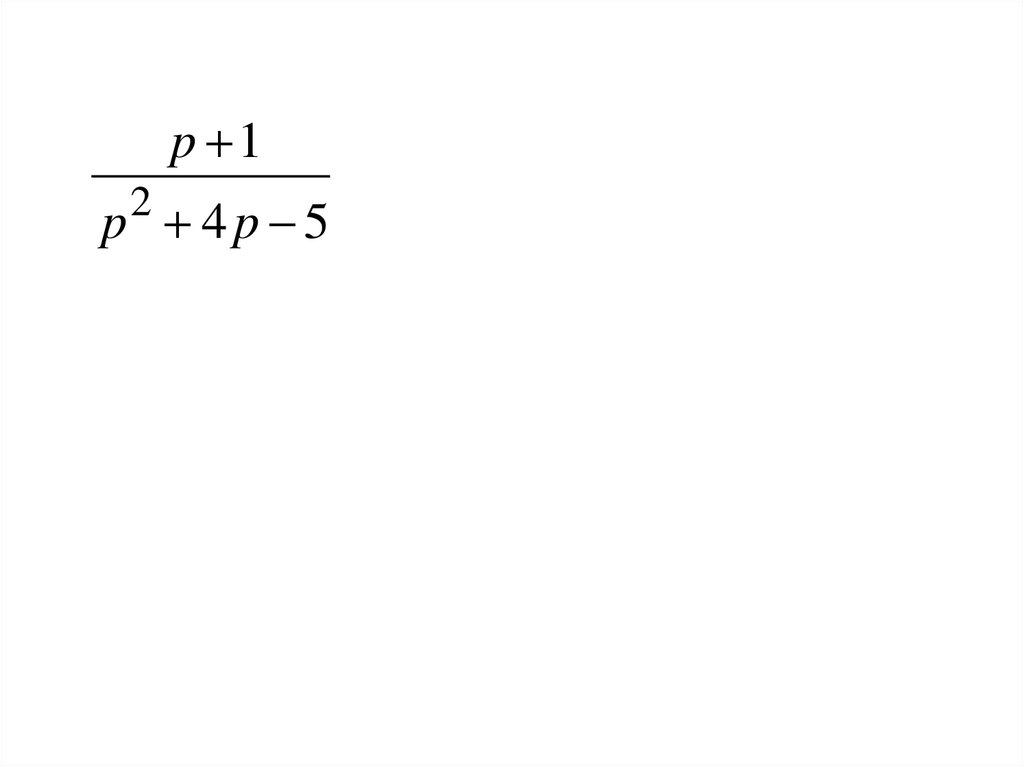
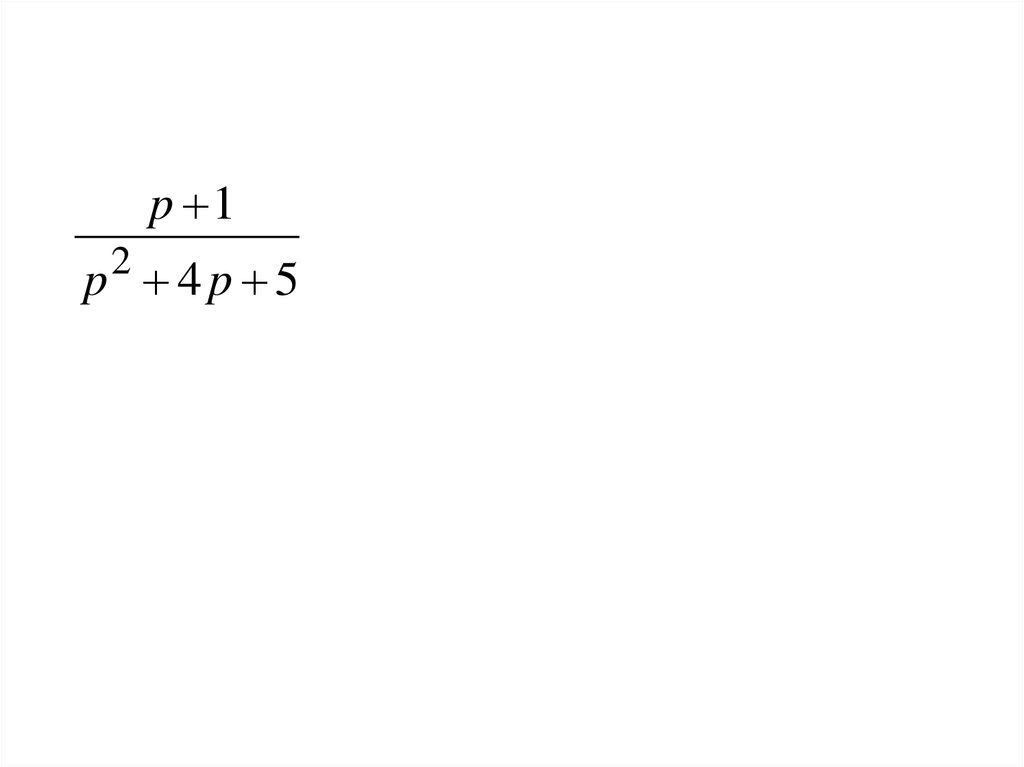









 Математика
Математика








