Похожие презентации:
ДУ высших порядков. Решение ОЛДУ второго порядка с постоянными коэффициентами
1. Математика Часть 2
УГТУ-УПИ2007 г.
2.
Лекция 13ДУ высших порядков.
1. Решение ОЛДУ второго порядка с
постоянными коэффициентами.
Рассмотрим ОЛДУ второго порядка:
y
py
qy 0,
p, q
где
- постоянные.
Будем искать решение уравнения в виде:
y e kx , k const .
y
ke kx , y
k 2e kx .
Подставим это в
:
3.
k e pke qe 0,2 kx
kx
kx
k pk q 0.
2
Уравнение k pk q 0 называется
характеристическим уравнением ОЛДУ.
(Из него определяют k)
2
Решения характеристического уравнения:
2
p
p
k1,2
q.
2
4
4.
Возможны 3 случая:1) Корни характеристического уравнения
действительные и разные.
p
q 0
4
2
k1 k2
Уравнение имеет два линейно
независимых частных решения:
y1 e , y2 e .
k1 x
Общее решение:
k2 x
y c1e
k1 x
c2 e
k2 x
5.
Пример .Найти общее решение ОЛДУ
y
2 y
8 y 0.
Решение.
k 2k 8 0,
2
k1 4,
y c1e
k2 2,
4x
c2 e
2 x
.
6.
2) Корни характеристического уравнениядействительные и одинаковые.
p
q 0
4
2
p
k1 k2 k
2
Одно частное решение: y1 e
p
x
2
.
Можно показать,что второе линейно независимое
частное решение имеет вид:
y2 y1 x e
p
x
2
x.
7.
Для этого достаточно показать,что определительВронского для y1 и y2 не равен нулю:
W y1 , y2
y1
y2
e kx
kx
ke
y1 y2
xe kx
2 kx
e
0
kx
e (1 xk )
8.
Пример .Найти общее решение ОЛДУ
y
6 y
9 y 0.
Решение.
k 6k 9 0,
2
k1 k2 3 9 9 3,
y c1e
3x
c2 xe
3x
c1 c2 x e .
3x
9.
3) Корни характеристического уравнениякомплексные.
k1 i ,
k2 i
p 2
q 0
4
2
где
p
p
, q .
2
4
Частные решения имеют вид:
y1 e
i x
, y2 e
i x
.
10.
Ранее было показано, что если ОЛДУ имееткомплексное решение, то его реальная и мнимая
части также будут решениями этого уравнения:
y e
i x
x i x
e e
x
e (cos x i sin x )
y1 e x cos x ðåàëüí àÿ ÷àñò ü ðåø åí è ÿ
x
y2 e sin x ì í è ì àÿ ÷àñò ü ðåø åí è ÿ
11.
Определитель Вронского для этих y1 и y2 неравен нулю (показать самостоятельно), значит
они линейно не зависимы.
Следовательно, общее решение уравнения равно
их линейной комбинации:
x
x
y C1e cos x C 2e sin x ,
è ëè
x
y e (C1 cos x C 2 sin x )
12.
Пример.Найти общее решение ОЛДУ
y
6 y
13 y 0.
Решение.
k 6k 13 0,
2
k 3 2i , 3, 2,
y e
3x
c1 cos 2 x c2 sin 2 x .
13.
Решение ОЛДУ n-го порядка спостоянными коэффициентами
2.
Рассмотрим ОЛДУ n-го порядка:
y
n
a1 y
n 1
... an y 0, ai const
y1 x , y2 x , ..., yn x
Функции :
называются линейно независимыми
на a , b , если
c1 y1 c2 y2 ... cn yn 0,
только в случае когда все сi 0.
14.
Т.y1 , y2 ,..., yn
Если функции
являются линейно независимыми частными
решениями ОЛДУ n-го порядка, то его общее
решение равно их линейной комбинации:
y c1 y1 c2 y2 ... cn yn ,
где ci
- произвольные постоянные.
Число линейно независимых частных решений
равно порядку ОЛДУ или степени
характеристического уравнения.
15.
Составим характеристическое уравнение для ОЛДУn-го порядка с постоянными коэффициентами
n 1
k a1k
n
Найдём корни
a2 k
n 2
... an 0.
k1 , k2 , ...kn .
В зависимости от корней характеристического
уравнения, частные линейно независимые
решения ОЛДУ имеют разный вид.
1) Каждому действительному однократному
корню k соответствует частное решение вида
y e kx .
16.
2) Каждому действительному корню kкратности r соответствует r линейно
независимых решений :
y1 e kx ,
kx
y2 xe ,
2 kx
y3 x e ,
..................
yr x r 1 e kx
17.
3) Каждой паре комплексных корнейk1,2 i
соответствуют два частных решения :
x
y1 e cos x ,
x
y2 e sin x
18.
4) Каждой паре комплексных корней k1,2 iкратности m соответствуют 2m частных
решений :
y1 e x cos x ,
x
y
xe
cos x ,
2
...........
m 1 x
ym x e cos x ,
x
y
e
sin x ,
m 1
............
m 1 x
y2 m x e sin x
19.
Пример.Найти общее решение ОЛДУ
Решение.
k 1 0,
3
k 1 k
k1 1, k2,3
y c1e e
x
x
2
2
y
y 0.
k 1 0,
1
3
i
.
2
2
3
3
c2 cos
x c3 sin
x
.
2
2
20.
3. Решение НЛДУ второго порядкаНЛДУ второго порядка имеет вид:
y
a1 y
a2 y f x ,
где
a1 , a2, f x
известные функции.
Т. Общее решение НЛДУ y равно сумме общего
решения y0 соответствующего однородного
''
'
уравнения
y0 a1 y0 a2 y0 0
и любого частного решения y% данного
a1 y%
a2 y% f x :
неоднородного уравнения y%
%
y y0 y
21.
Доказательство:Для y0 , y% справедливо:
''
'
y%
a1 y%
a2 y% f x .
y0 a1 y0 a2 y0 0,
Сложим уравнения почленно
y0 y%
a1 y0 y%
a2 y0 y% f x ,
y y0 y%- решение уравнения.
Докажем, что при любых начальных условиях
y x 0 y0 , y
x0 y0
можно подобрать c1 , c2 так, чтобы решение
удовлетворяло этим начальным условиям.
22.
Пустьy0 c1 y1 c2 y2 ,
y c1 y1 c2 y2 y%
Подставим начальные условия
y
y
10
20
%
y
c
y
c
y
y
,
0 1 10 2 20 0
W x0
0,
y10 y20
y%
y0 c1 y10 c2 y20
0
т.к. y1 , y2 - линейно независимы
Система уравнений имеет единственное
решение c1 , c2 .
23.
Решение НЛДУ второго порядка методомвариации произвольных постоянных.
Пусть известно общее решение ОЛДУ
y0 c1 y1 c2 y2 ,
где
c1 , c2 -const.
Будем искать частное решение НЛДУ в виде
y% c1 x y1 c2 x y2 , c1 , c2 - функции от x .
y%
c1 y1
c1
y1 c2 y2
c2
y2 .
c1 x , c2 x
Подберём
так, чтобы
c1
y1 c2
y2 0, тогда
y%
c1 y1
c2 y2
,
24.
y%c1 y1
c1
y1
c2 y2
c2
y2
.
Подставим это в НЛДУ
c1
y1
c2 y2
c2
y2 +a1 c1 y1
c2 y2
c1 y1
+a2 c1 y1 c2 y2 f x ,
0
0
c1 y1
a1 y1
a2 y1 +c2 y2
a1 y2
a2 y2
+c1
y1
c2
y2 f x .
c1
y1
c2
y2 f x .
25.
c1 x , c2 xудовлетворяют системе:
y1 y2
c
y
c
y
0,
1 1 2 2
W y1 , y2
0,
y
y
c1
y1
c2
y2 f x .
1
2
( y1 , y2 - линейно независимы.)
Система уравнений имеет единственное
решение c1
1 x , c2
= 2 x .
Тогда
c1 x
1 x dx ,
c2 x
2 x dx .
26.
Пример.Найти общее решение НЛДУ
y
y
x.
x
Решение.
y
y
0.
Найдем решение ОЛДУ
x
1
y
cx ,
, ln y ln x ln c , y
y x
2
2
y1 x , y2 1.
y0 c1 x c2 ,
Ищем частное решение НЛДУ в виде:
2
%
%
y c1 x y1 c2 x y2 , y c1 x x c2 x .
27.
c1y1 c2
y2 0,
c1
y1
c2
y2 f x .
1
1 2
c1
, c2 x ,
2
2 3
좢
c1 x c2
1 0,
2 xc1
0
c2 x .
2
x
x
c1 , c2
.
2
6
3
x 2 x
2
y x
1 c1 x c2
2 6
3
3
3
x x
x
2
2
c1 x c2 c1 x c2 .
2 6
3











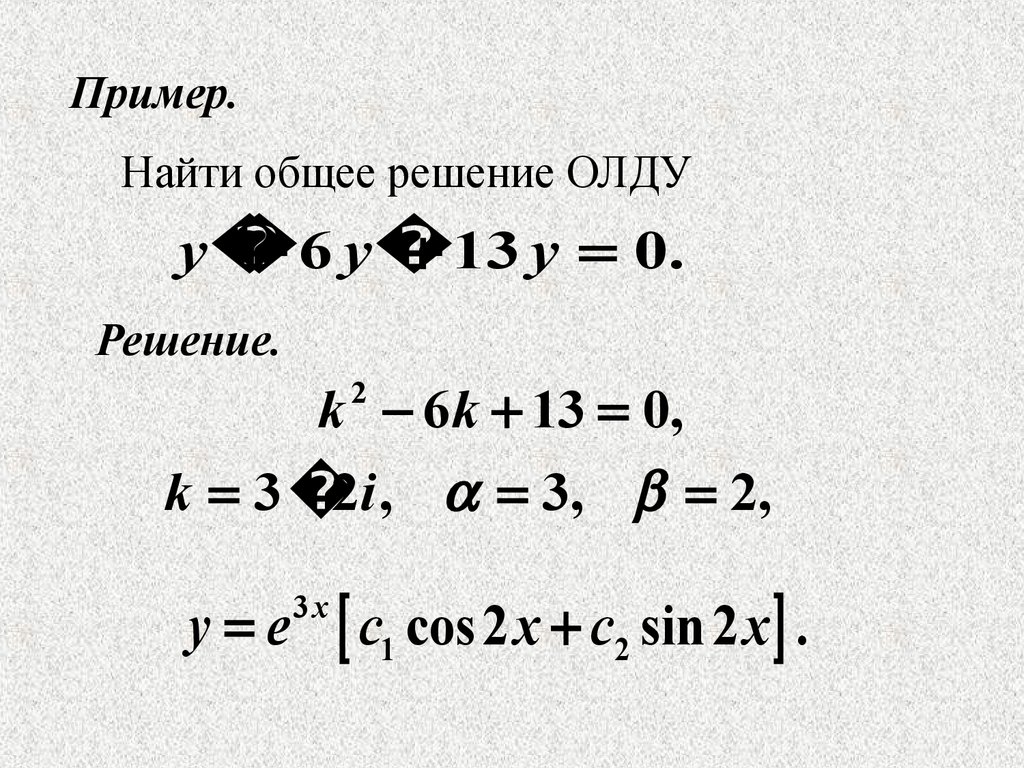















 Математика
Математика








