Похожие презентации:
Решение задач на нахождение расстояний и углов в пространстве с помощью метода координат. Задание С2
1. Решение задач на нахождение расстояний и углов в пространстве
с помощью метода координат.Задание С2
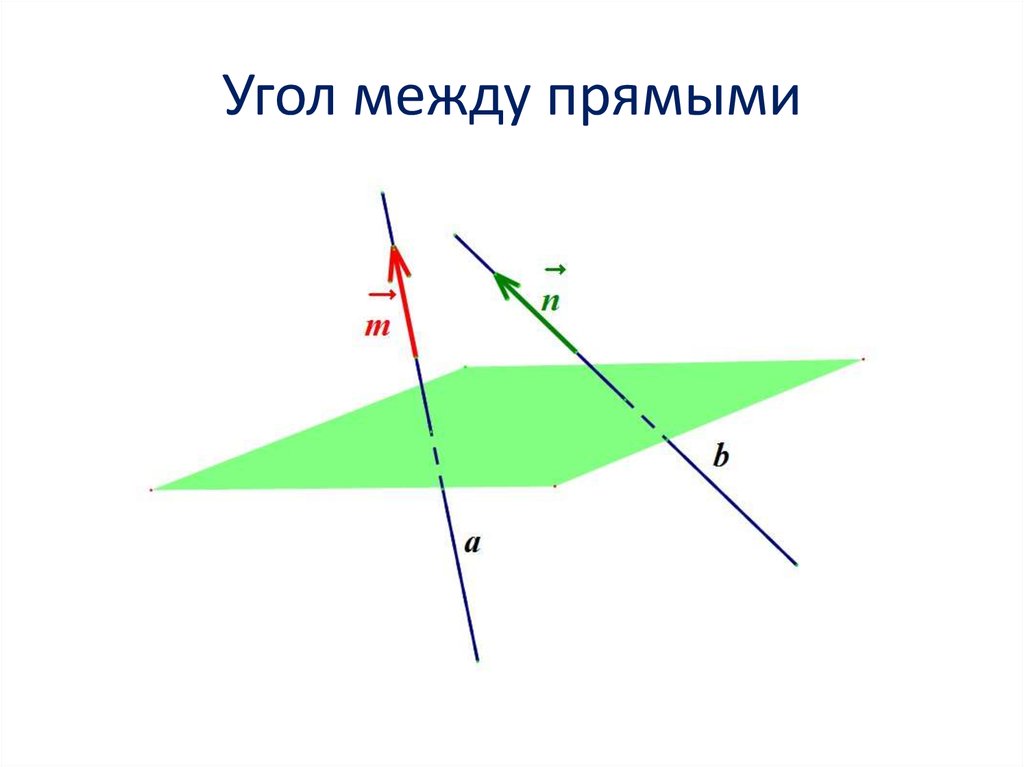
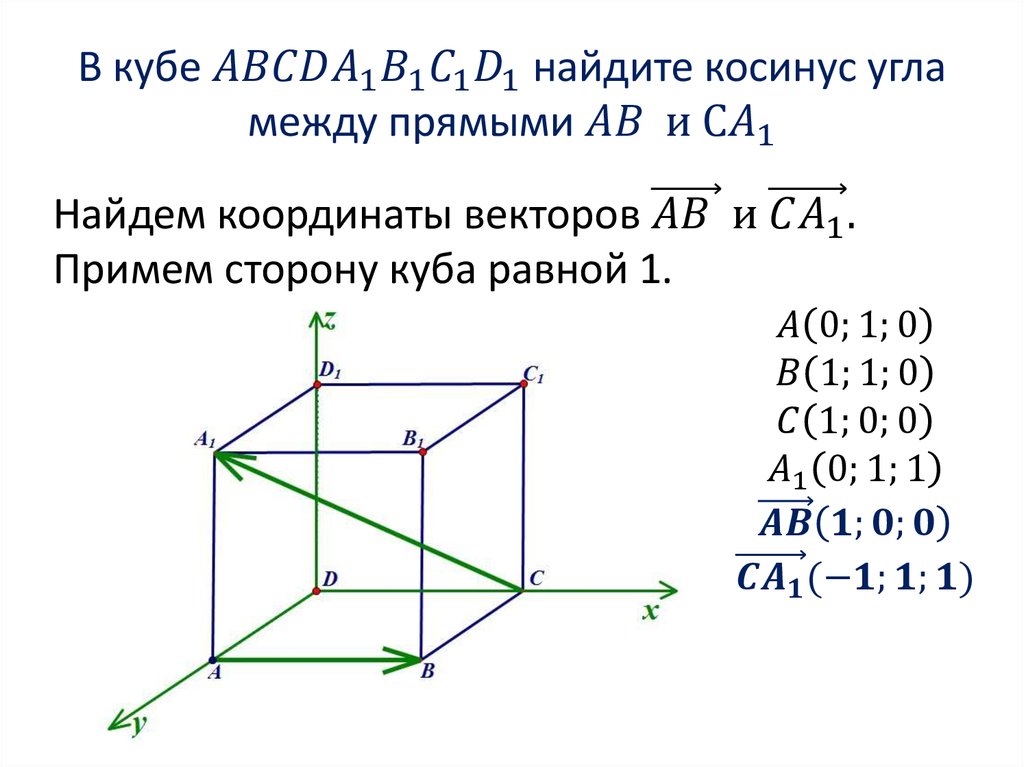
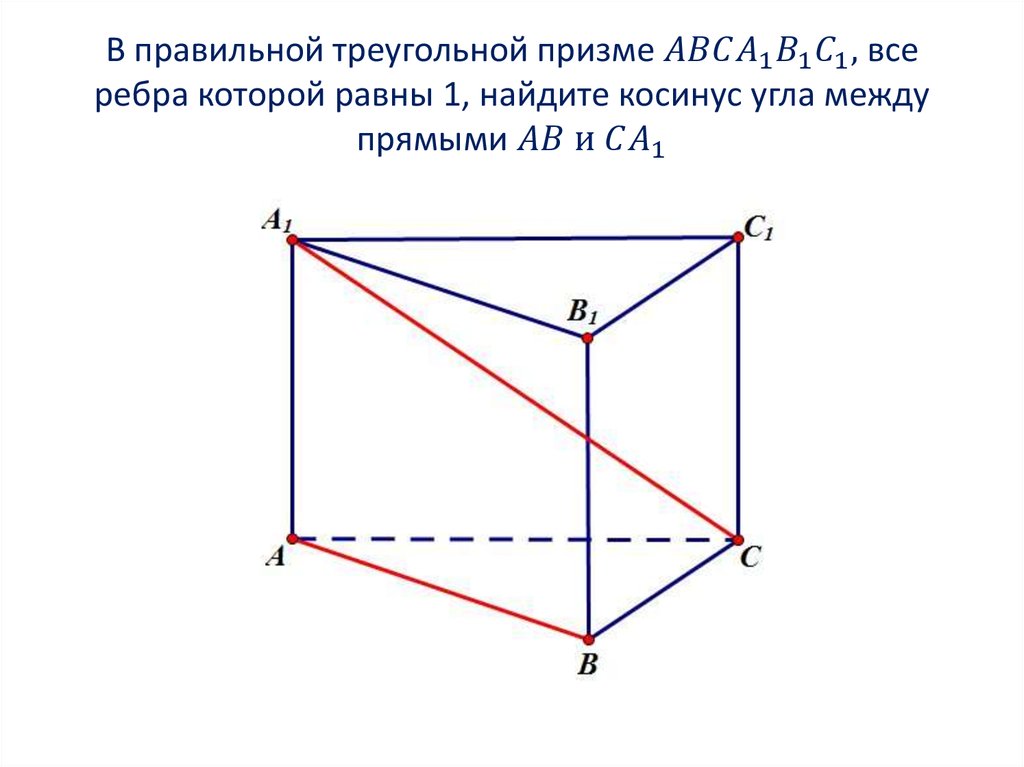
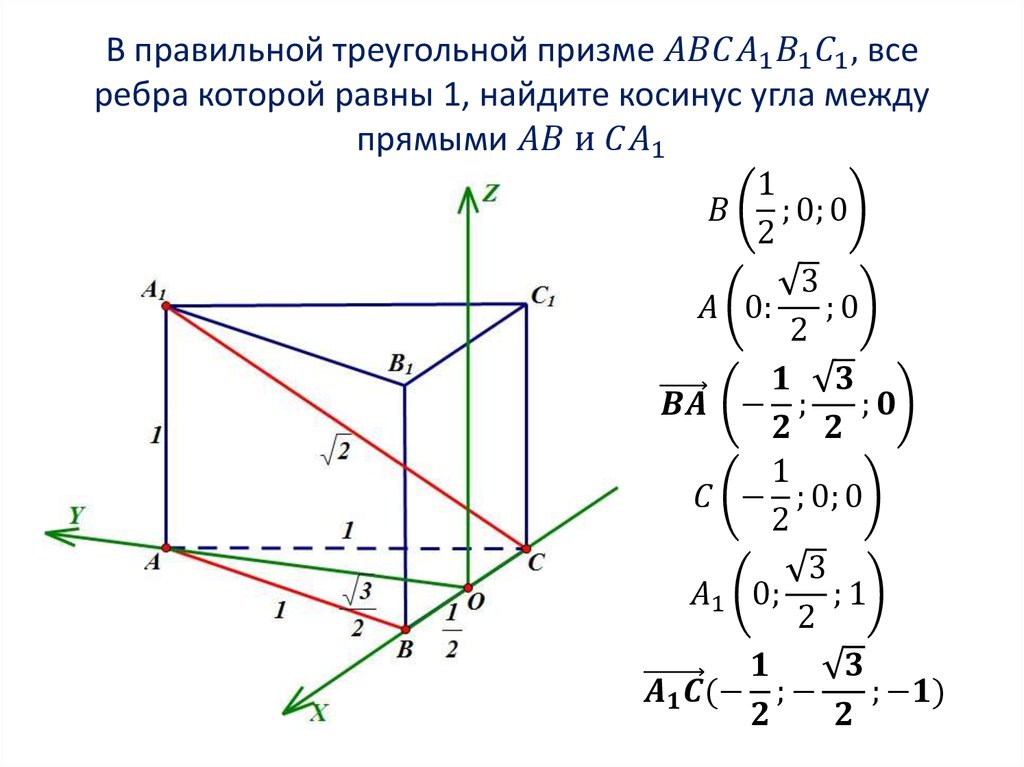
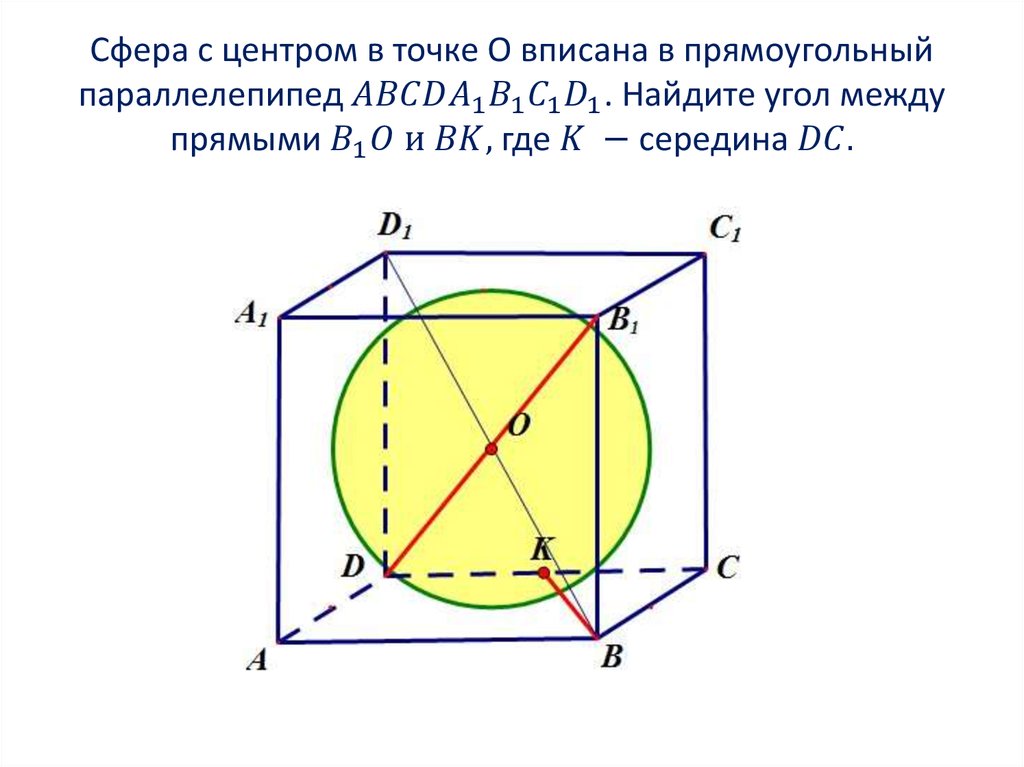
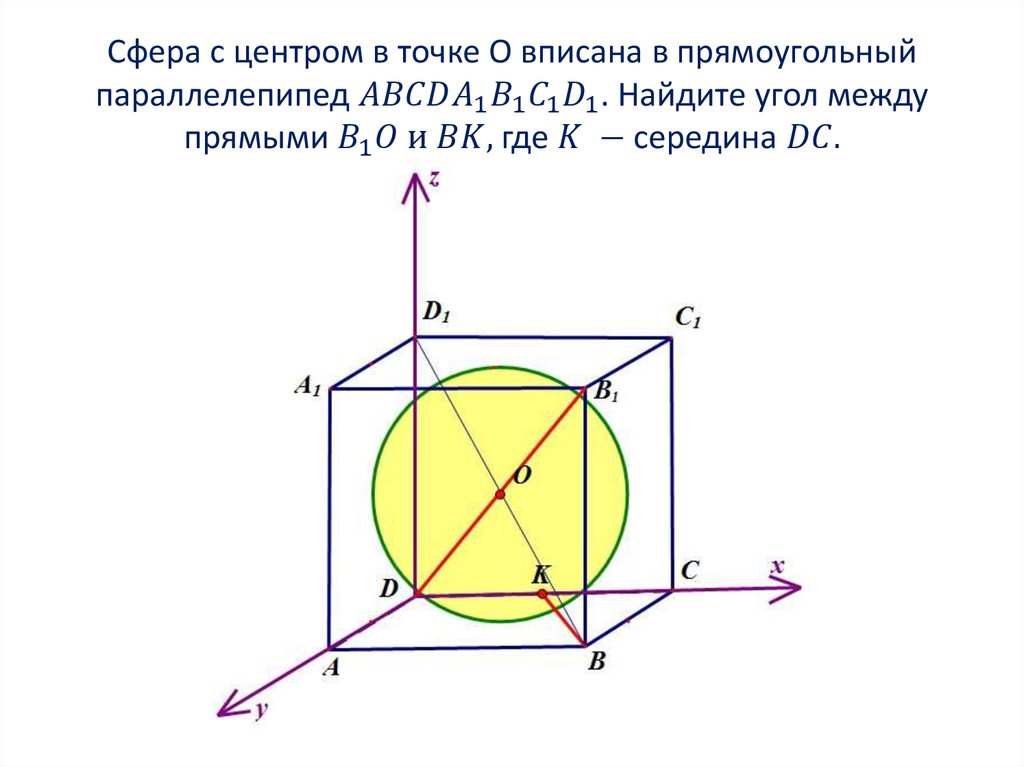
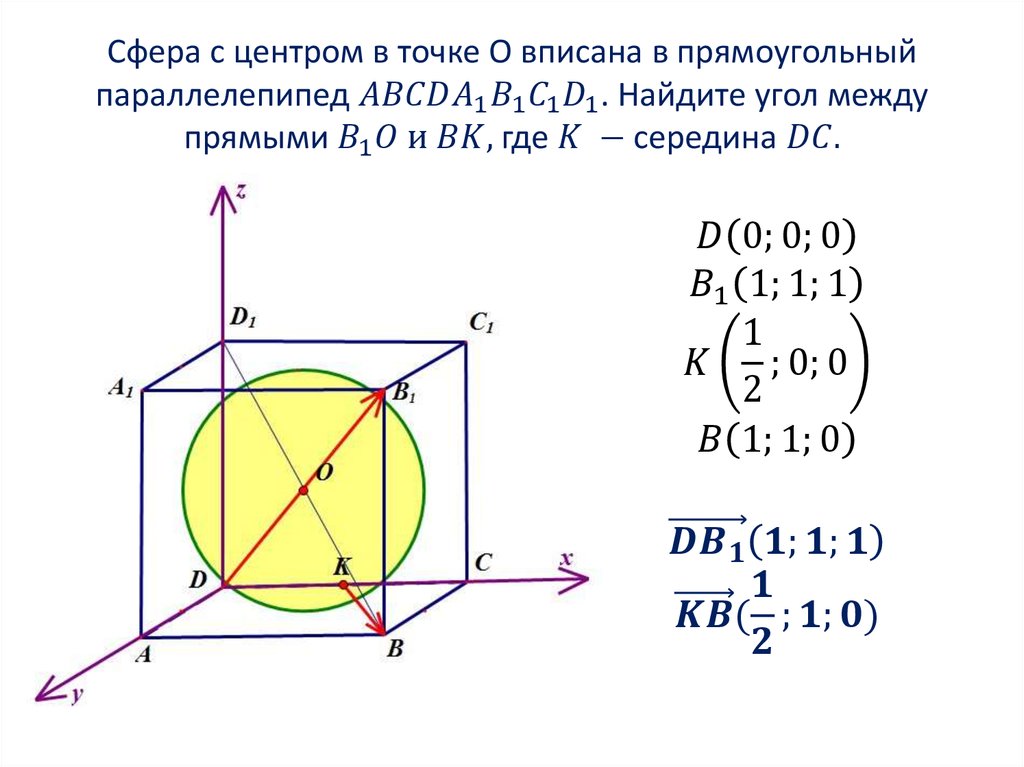
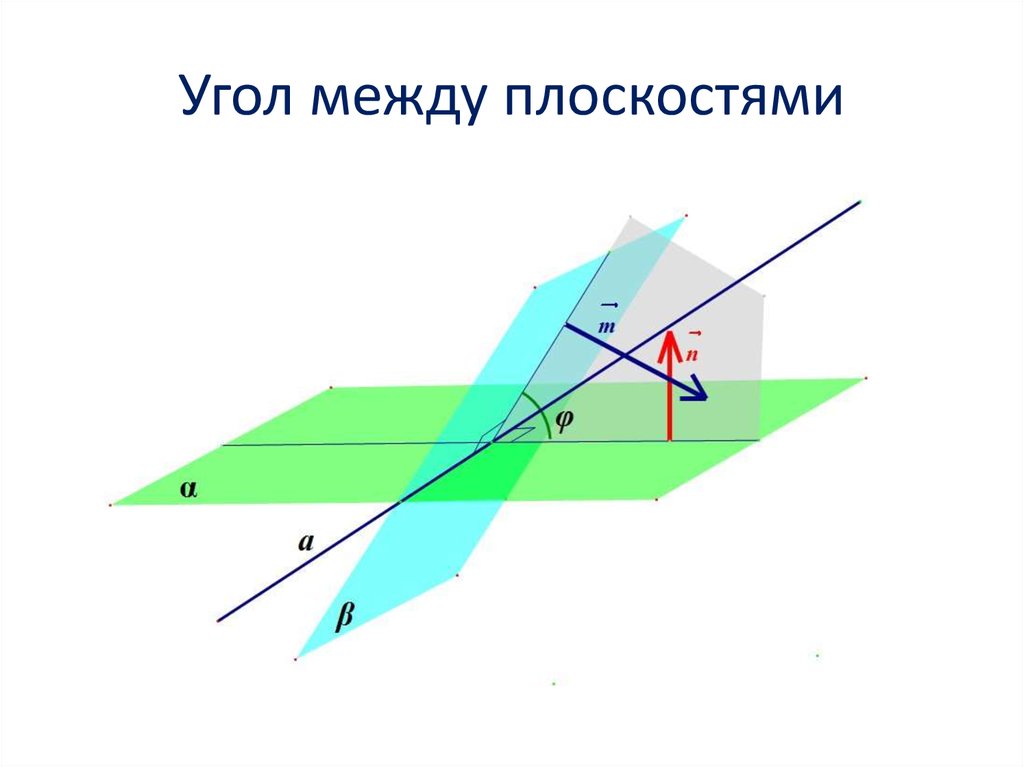
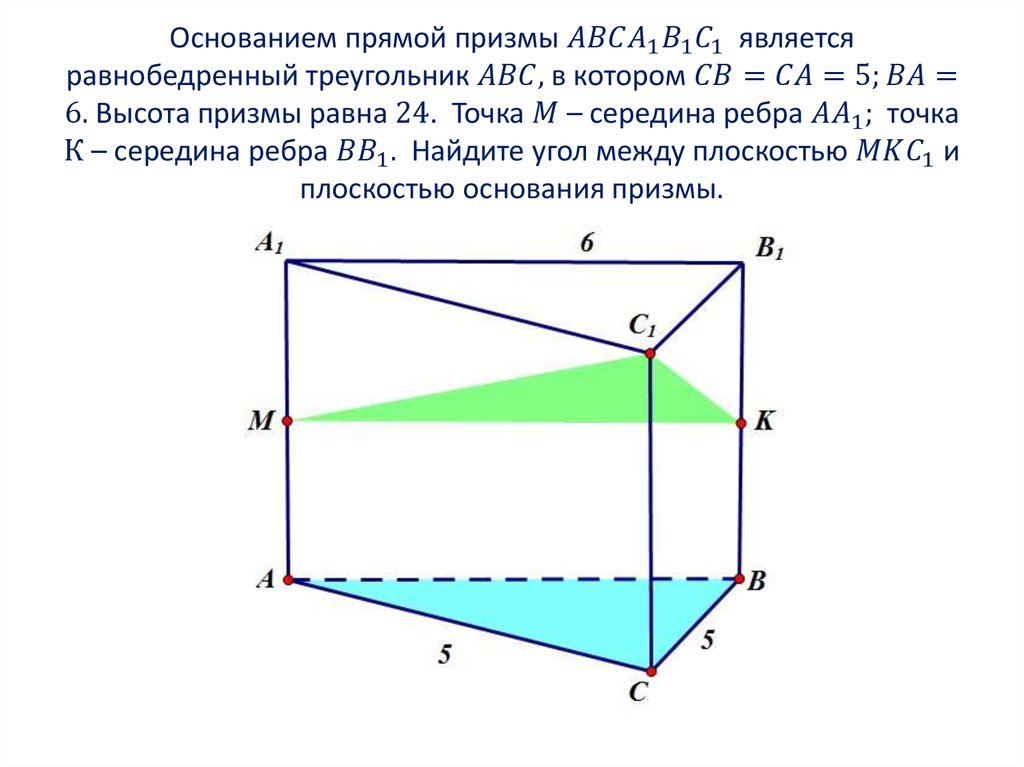
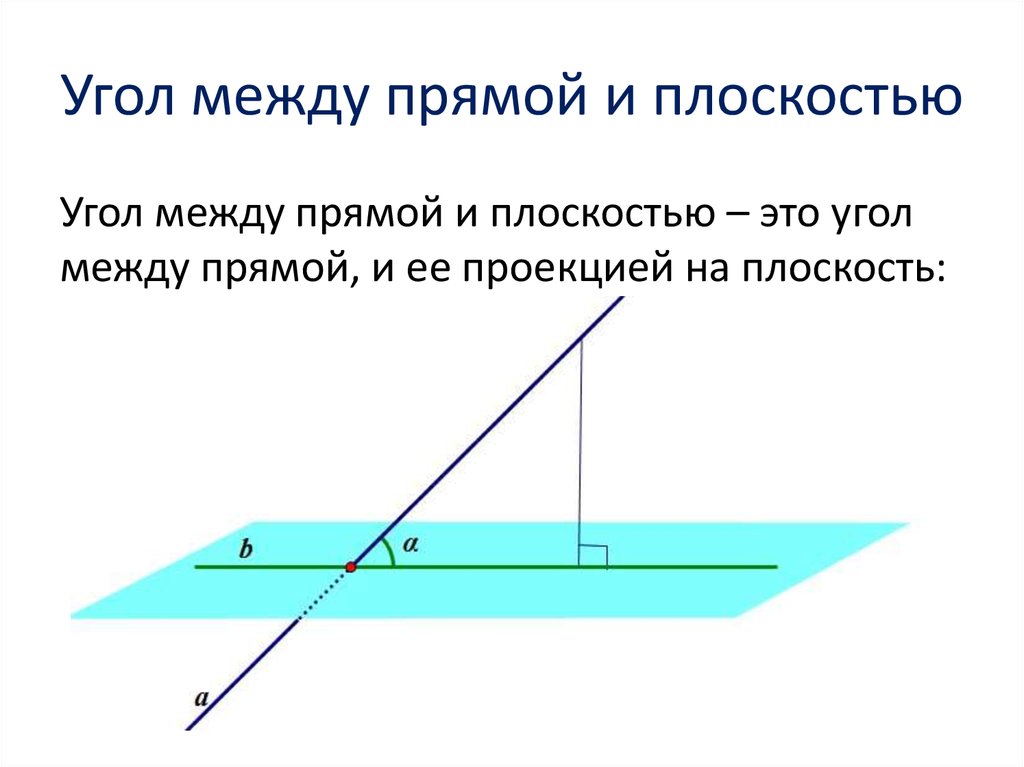
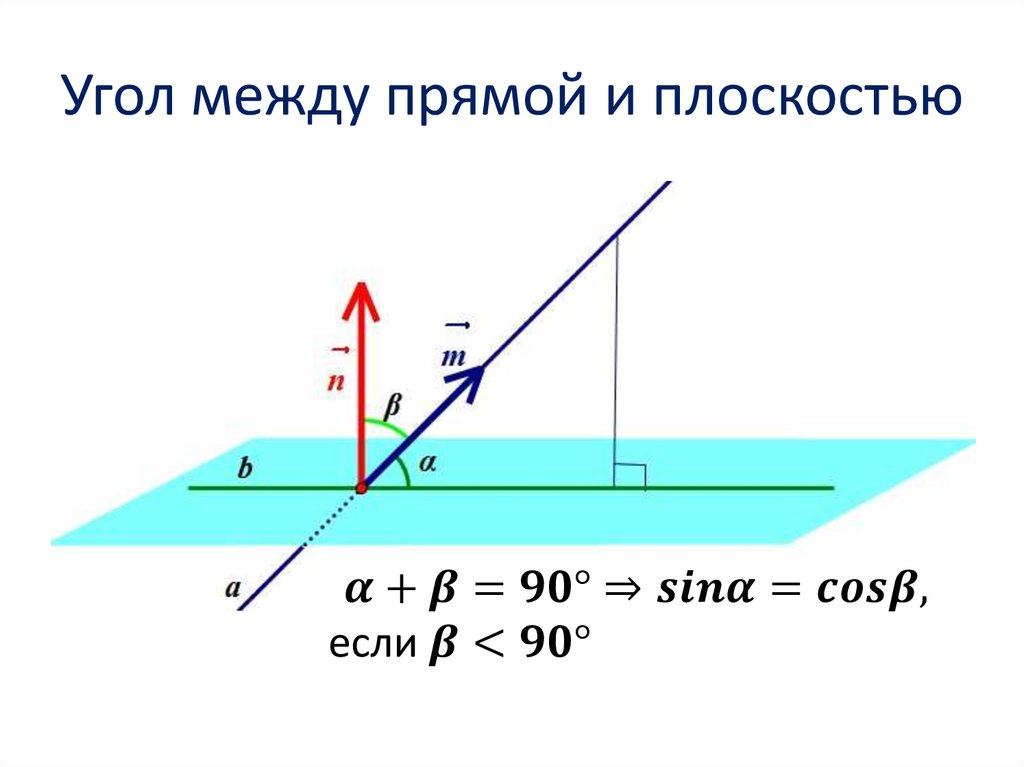
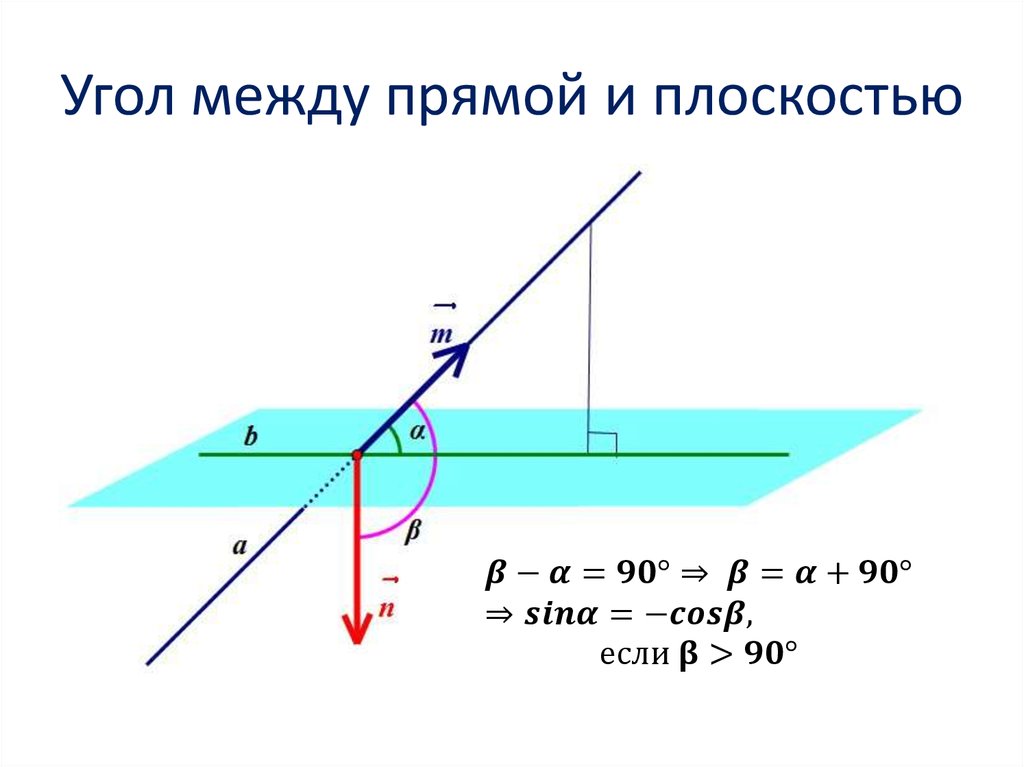
2. Угол между прямыми
3. Угол между прямыми
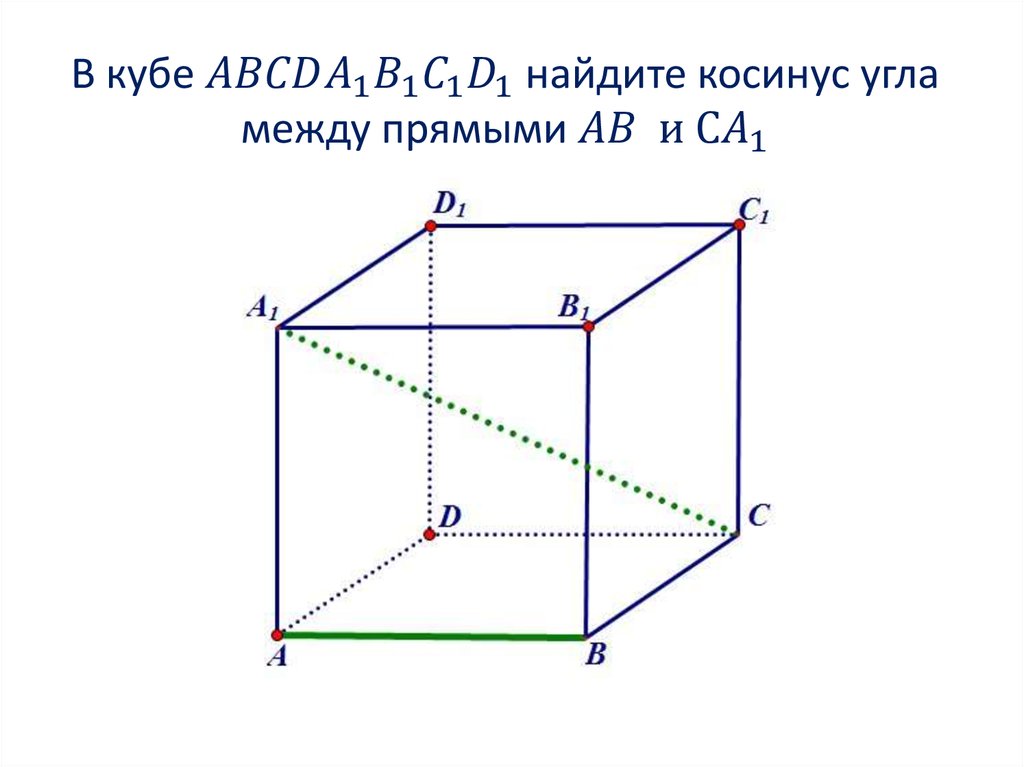
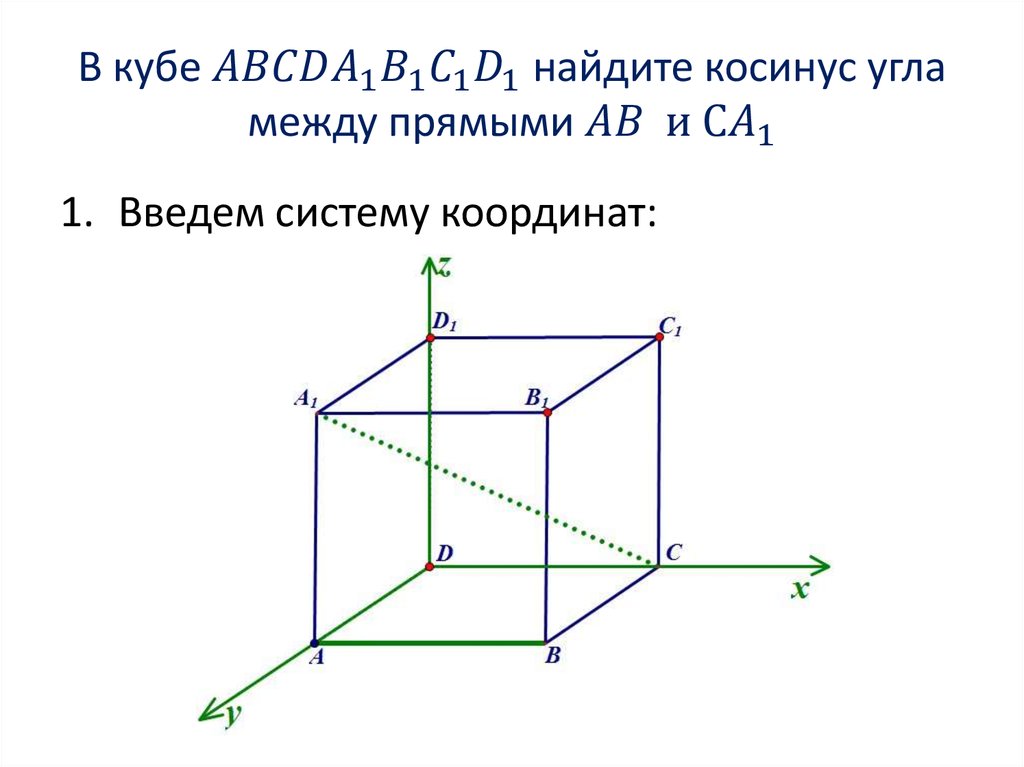
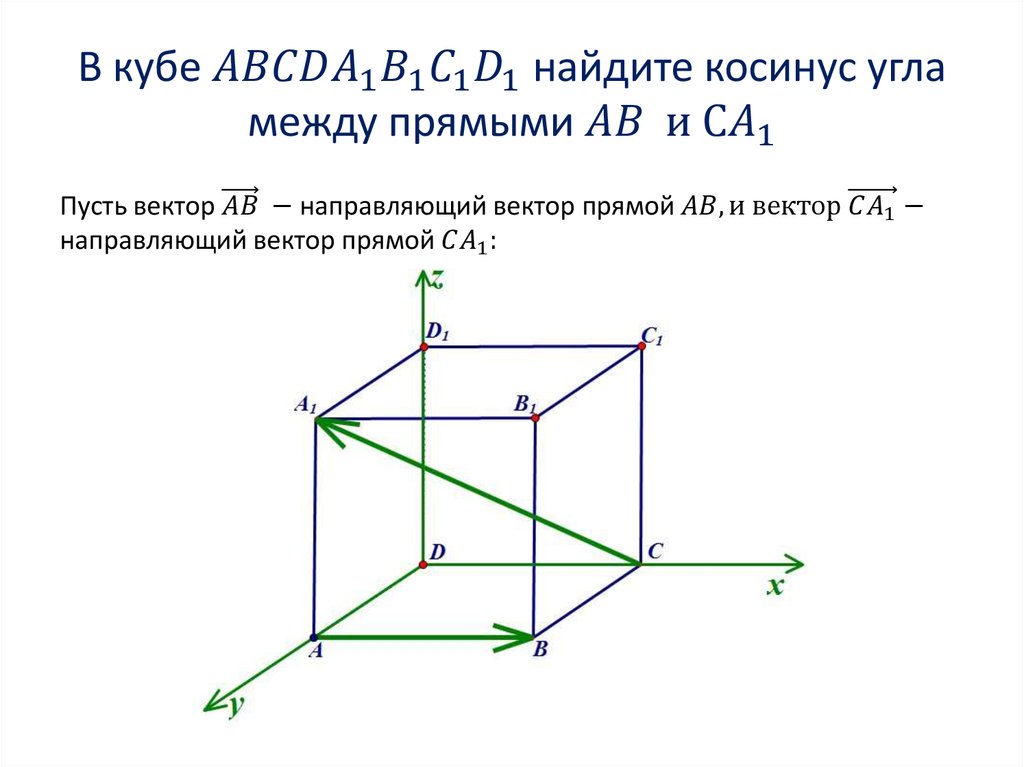
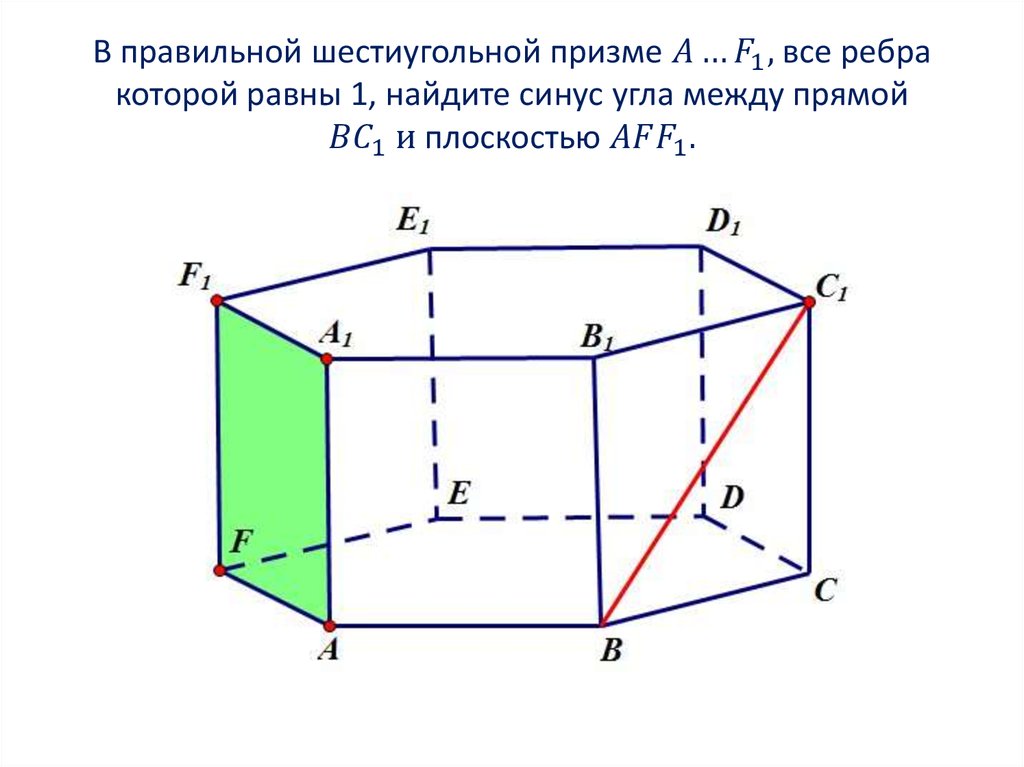
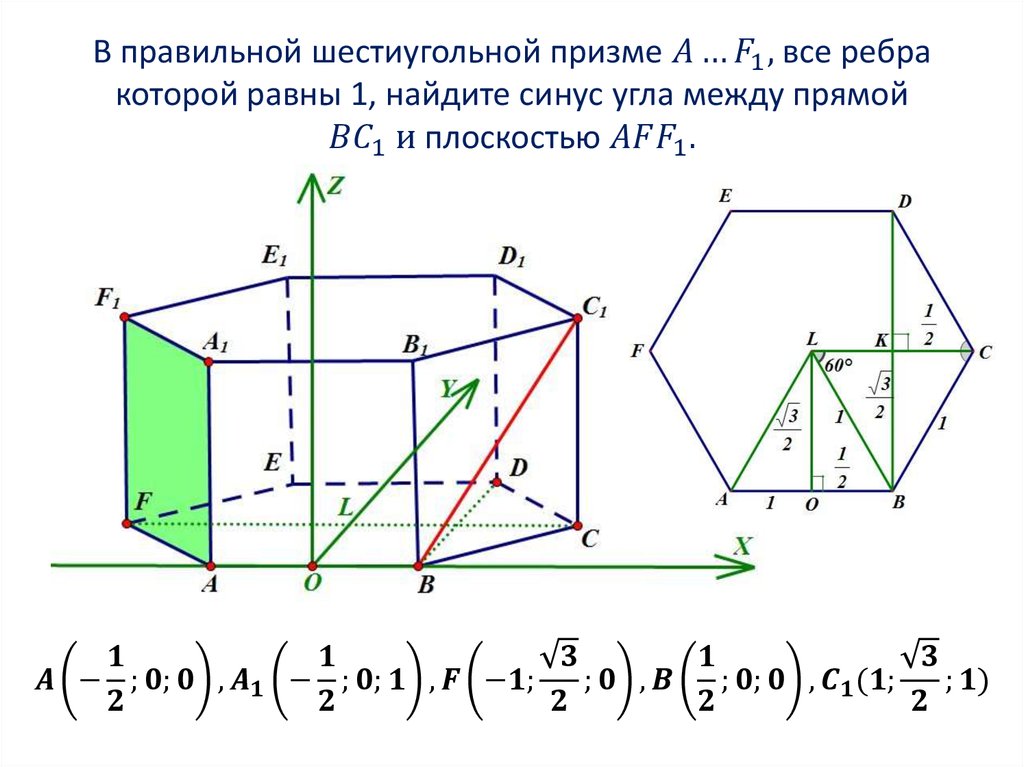
1. Находим координаты направляющихвекторов прямых. Если прямая проходит через две
точки, которые являются концами отрезка, то для того,
чтобы найти направляющий вектор прямой, нужно из
координат конца отрезка вычесть координаты начала:


























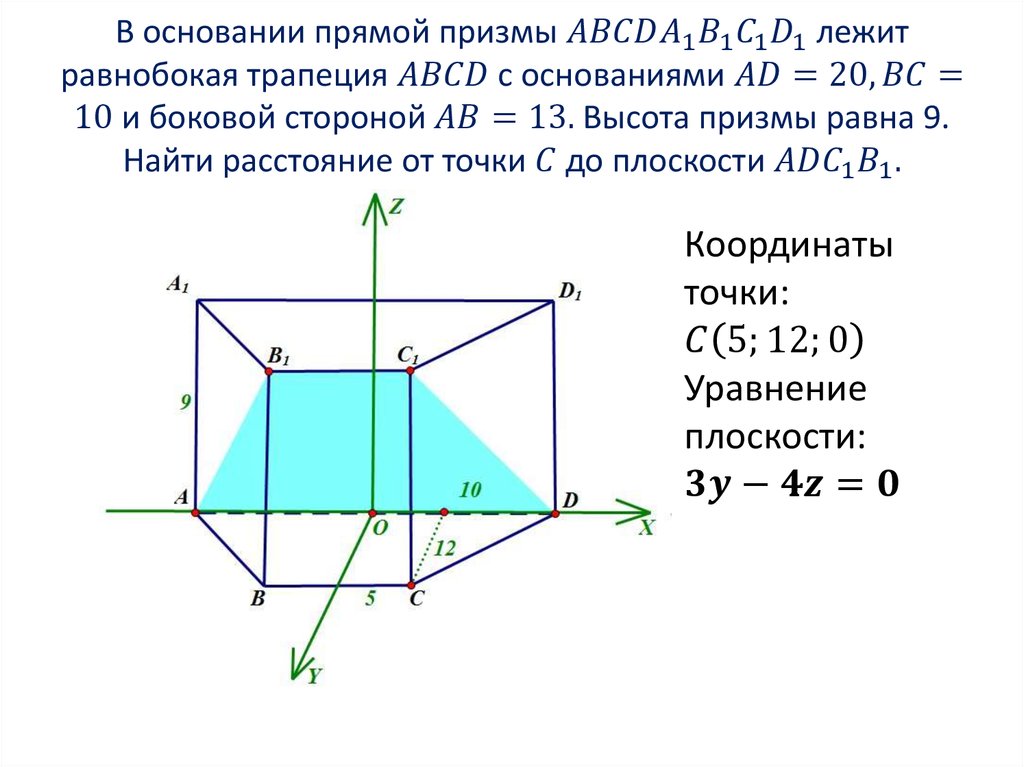


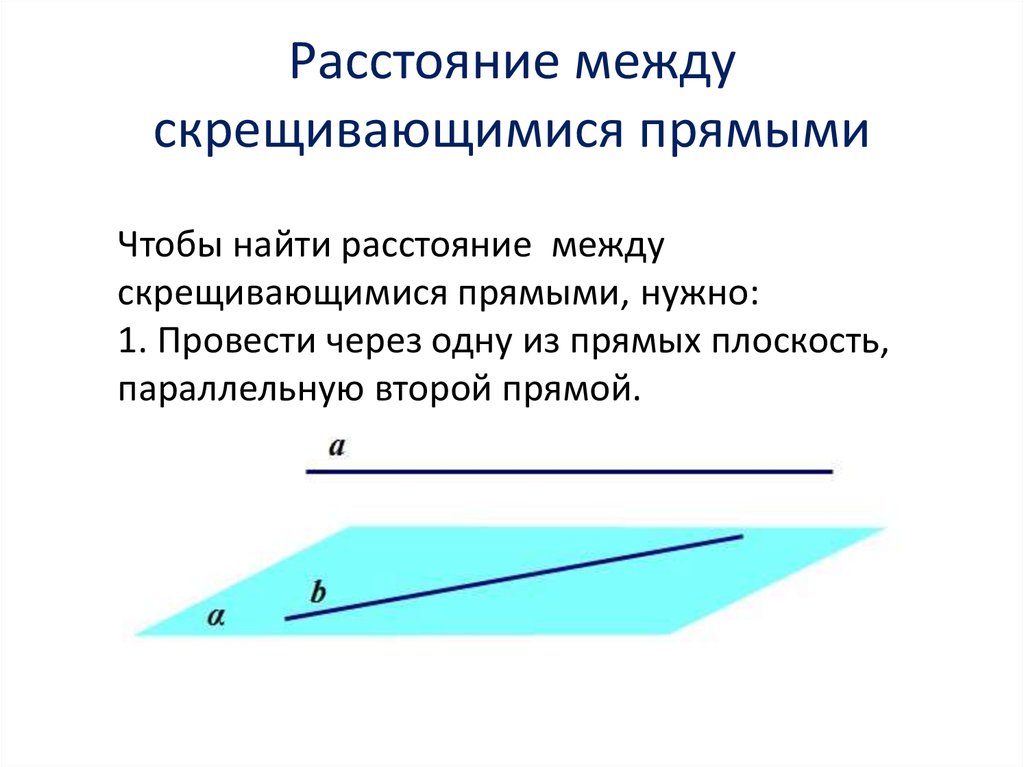
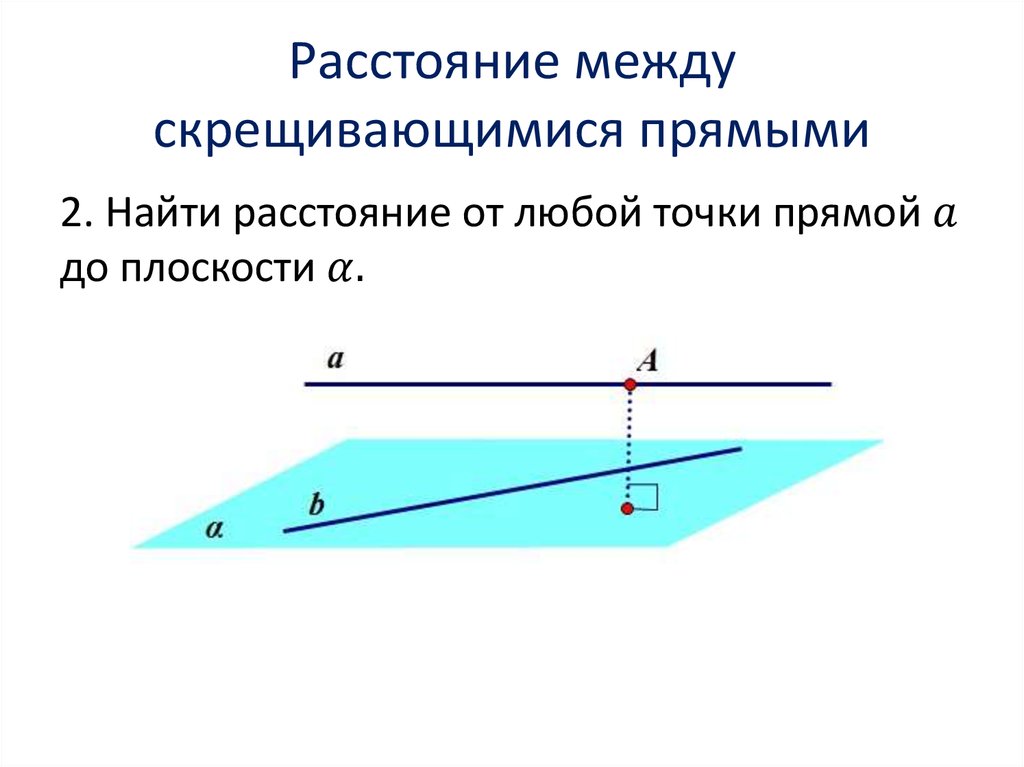
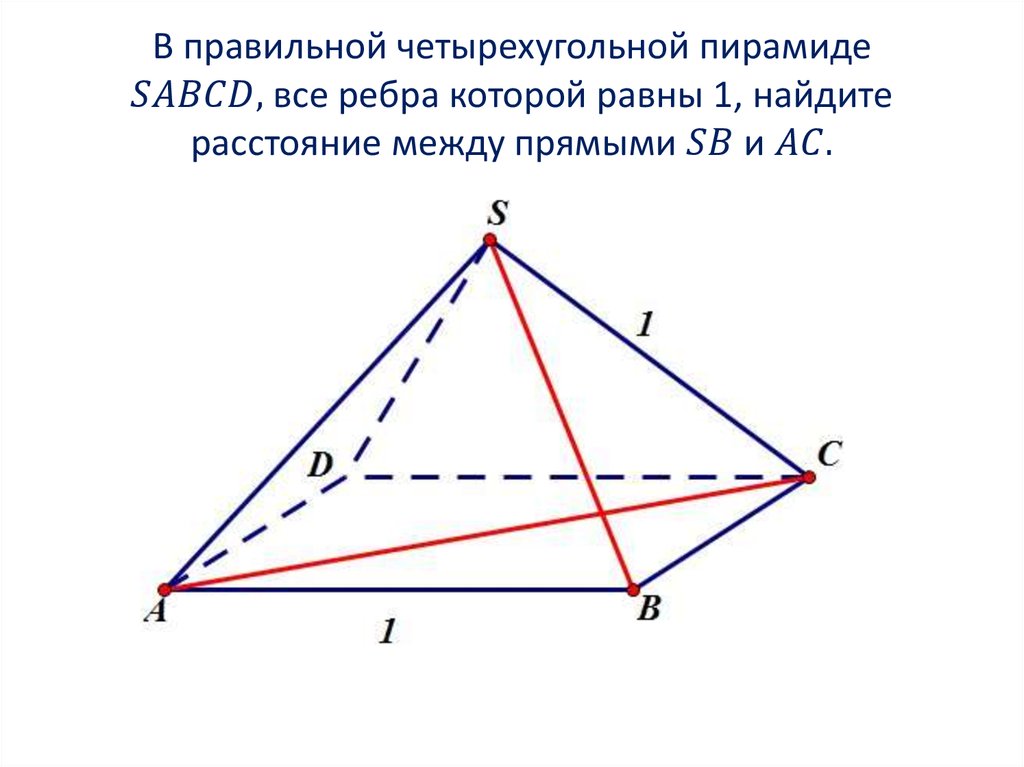
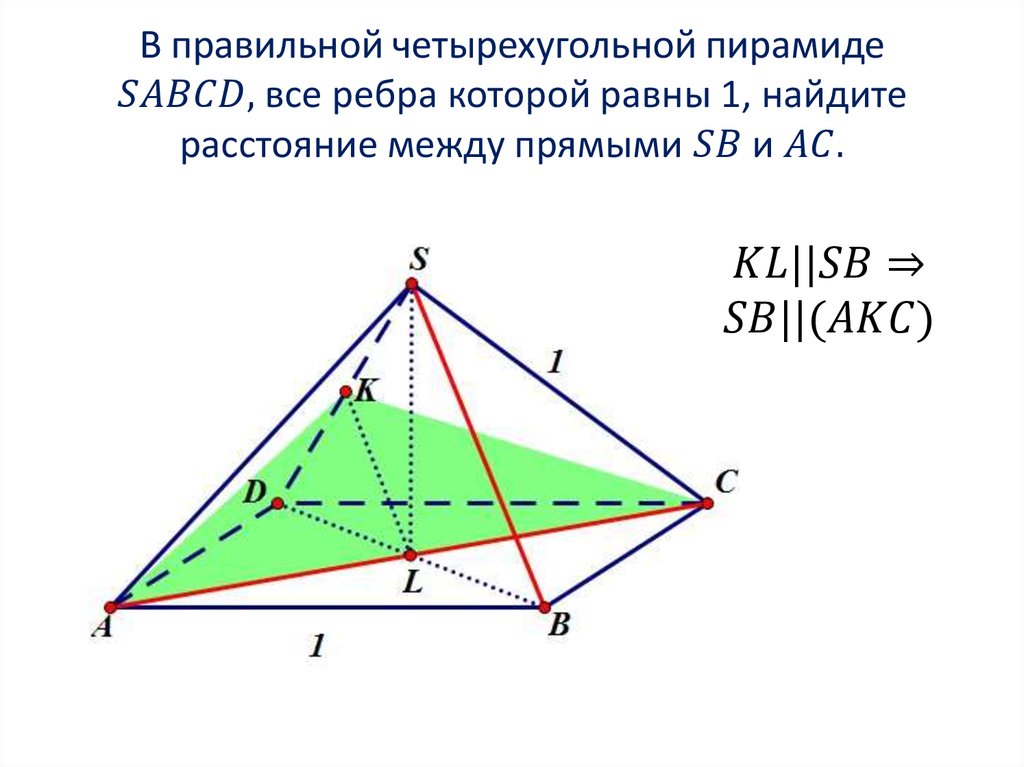
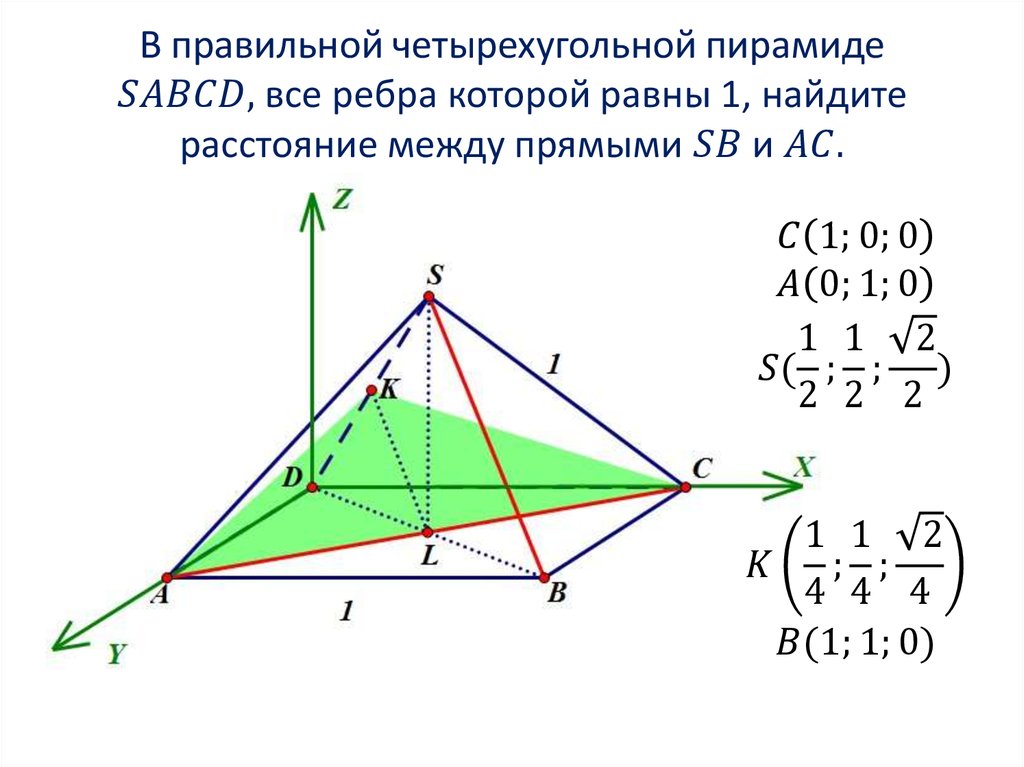










 Математика
Математика








