Напряженное и деформированное состояния элемента в окрестности точки

1.

ФГАОУ ВПО «Северо-Восточный федеральный университет им. М.К. Аммосова»
Инженерно-технический институт
Кафедра прикладной механики
Решение задач
по дисциплине «Техническая механика»
270800 - Строительство

2. НАПРЯЖЕННОЕ И ДЕФОРМИРОВАННОЕ СОСТОЯНИЯ ЭЛЕМЕНТА В ОКРЕСТНОСТИ ТОЧКИ

3.

2
n
1
P
P
1
N
P
1
2
n
P
1
S
D
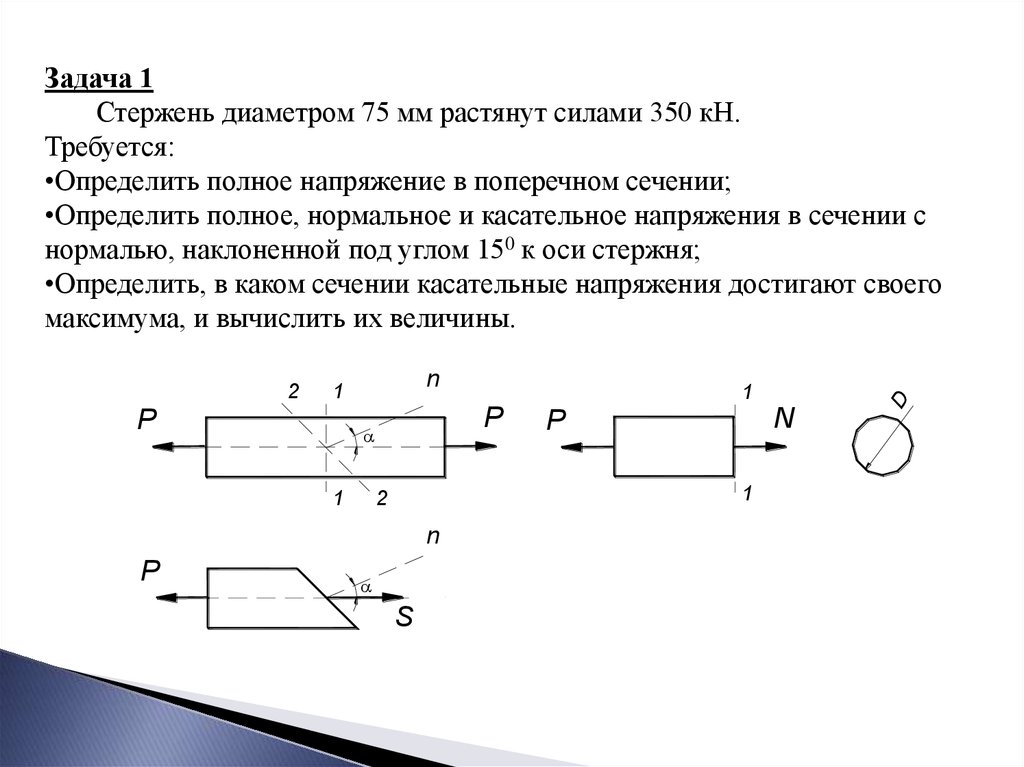
Задача 1
Стержень диаметром 75 мм растянут силами 350 кН.
Требуется:
•Определить полное напряжение в поперечном сечении;
•Определить полное, нормальное и касательное напряжения в сечении с
нормалью, наклоненной под углом 150 к оси стержня;
•Определить, в каком сечении касательные напряжения достигают своего
максимума, и вычислить их величины.

4.

Решение:
1. Рассматривая равновесие отсеченной
определяем внутреннее усилие N:
Z N P 0,
части сечением 1-1 части,
N P 350 кН.
Определяем полное напряжение в поперечном сечении 1-1, которое равно
нормальному напряжению:
p1 1
N 4 350 кН
кН
7,93
.
2
2
A 3,14 7,5
см
Из равновесия отсеченной части сечением 2-2 определяем внутреннее
усилие S:
Z S P 0,
S P 350 кН.
2. Выразим площадь сечения 2-2 через площадь поперечного сечения
A
стержня А:
A
cos15 0
Полное напряжение в сечении 2-2:
p
S
P
кН
cos15 0 cos15 0 7,66
.
2
A
A
см

5.

Нормальное напряжение в сечении 2-2:
кН
p cos15 cos 15 7,4 2 .
см
0
2
Касательное напряжение в сечении 2-2:
0
кН
p sin 15 sin 2 15 sin 30 1,98 2 .
2
2
см
0
3. Из
2
0
0
sin 2
видно, что касательные напряжения своего максимального значения
достигают в сечении, наклоненном под углом 450 к оси стержня:
max
7,93
кН
0
sin 90 3,965
.
2
2
см

6.

Задача 2
В котле с внутренним диаметром D=800 мм, длиной l=1,6 м и
толщиной стенки t=10 мм создается внутреннее давление, равное р=12
атм=12 105 Па.
Требуется:
•Определить напряжения, возникающие в стенке котла в поперечном и
продольном сечениях;
•Определить возникающие напряжения в сечении под углом 300 к
образующей стенки котла;
•Проверить прочность котла по 3-й и 4-й теориям прочности, если
=180 МПа.
а)
б)
T
p=12 атм
D
T
в)
1
2
2
d
L
n
1

7.

Решение:
1. Стенка котла от действия внутреннего давления подвержена плоскому
напряженному состоянию.
Нормальные напряжения в поперечном сечении котла определяются из:
Q
p D 2 p D 12 105 0,8
7
2
2
,
4
10
Па 24 МПа,
2
A1 4 D t
4 t
4 1 10
где
p D 2
– растягивающие усилия стенки котла от
Q
4
торцевой части;
давления
A1 D t
– поперечное сечение стенки котла.
Нормальные напряжения в сечении вдоль образующей стенки котла,
вызванные тангенциальными усилиями, определяются:
T
p D 12 10 5 0,8
7
1
4
,
8
10
Па 48 МПа,
2
A2
2 t
2 1 10

8.

где
A2 l t , T p D l S / -2 тангенциальное усилие, которое получается из
Y 2T pl sin dS 0
dS R d , S D
0
2. Нормальные и касательные напряжения в сечении под углом 300 к
образующей определяем:
2 cos 2 1 sin 2 24 0,75 48 0,25 30 МПа,
1 2
2
48 24
sin 2
sin 600 10,4 МПа.
2
3. Проверка прочности стенки котла:
•по 3-й теории прочности (по наибольшим касательным напряжениям):
экв 1 3 48 0 48 МПа 180 МПа
3
•по 4-й теории прочности (энергетической теории прочности):
1
2
экв [ ( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 ]
4
12 22 1 2 482 24 2 48 24 41,57 МПа 180 МПа
Материал стенки котла по 3-й и 4-й
теориям отвечает условиям прочности.

9.

Задача 3
В элементе конструкции, подверженному плоскому напряженному
состоянию, в окрестности некоторой точки действуют напряжения:
x= –140 МПа, y=80 МПа,
xy=60 МПа.
Требуется определить:
• напряжения на площадке под углом (-350) к площадке с нормалью X;
• положение главной площадки и вычислить значения главных напряжений;
• значения главных напряжений, как экстремальные значения нормальных
напряжений, и сравнить с результатами п.2;
• величины максимальных касательных напряжений и показать площадку их
действия;
• наибольшие относительные линейные деформации элемента в окрестности
рассматриваемой точки, если Е=2,1 105 МПа, =0,25;
• величину удельной потенциальной энергии упругой деформации элемента;
• относительное изменение объема в окрестности, рассматриваемой точки;
•Проверить прочность материала элемента по 3-й и 4-й теориям прочности,
если =180 МПа.

10.

а)
y
yx
xy
1
x
xy
yx
y
ax
n
m
mi
x
б)
3
x
n
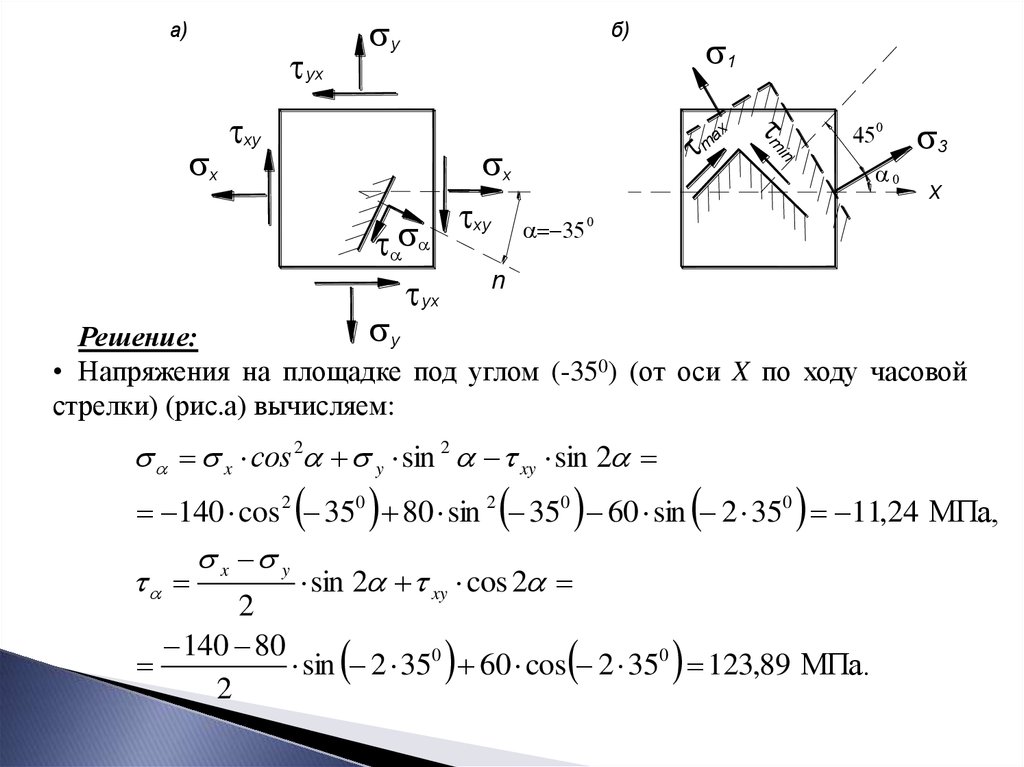
Решение:
• Напряжения на площадке под углом (-350) (от оси X по ходу часовой
стрелки) (рис.а) вычисляем:
x сos 2 y sin 2 xy sin 2
140 cos 2 350 80 sin 2 350 60 sin 2 350 11,24 МПа,
x y
sin 2 xy cos 2
2
140 80
sin 2 350 60 cos 2 350 123,89 МПа.
2

11.

• Главная площадка лежит под углом 0 к площадке с нормалью X:
2 xy
2 60
tg 2 0
0,545,
x y
140 80
2 0 arctg 0,545 28,59 0 ,
0 14,30.
Угол 0 откладываем против хода часовой стрелки от
0 >0.
оси X,
т.к.
Величины главных напряжений вычисляем:
x cos 2 0 y sin 2 0 xy sin 2 0
0
140 cos 2 14,30 80 sin 2 14,30 60 sin 28,6 0 155,3 МПа 3 ,
2
2
sin
cos
0 xy sin 2 0
x
0
y
0 90
140 0,061 80 0,94 60 0,479 95,3 МПа 1.

12.

•Значение главных напряжений вычисляем, как экстремальные значения
нормальных напряжений в окрестности рассматриваемой точки:
max
min
x y 1
140 80 1
2
2
2
x y 4 xy
140 80 4 602 30 125,3;
2
2
2
2
max 1 95,3 МПа,
min 155,3 МПа.
Сравнивая с результатами пункта 2, заключаем, что значения главных
напряжений и положения главных площадок вычислены верно.
•Величины максимальных касательных напряжений вычисляем:
max
1 3
2
min
или
max
min
1
2
x
y
2
4
2
xy
95,3 ( 155,3)
125,3 МПа,
2
1
2
140 80 2 4 60 2
125,3 МПа.
Площадки их действия лежат под углом 450 к
направлению главных площадок или от оси X на
=450+ 0=59,30 .

13.

• Наибольшие относительные линейные деформации вычисляем по
формулам обобщенного закона Гука, направления их совпадают с
направлениями главных напряжений:
1
1
5
1 1 2 3
95
,
3
0
,
25
155
,
3
63
,
87
10
,
5
E
2,1 10
1
0,25
5
2 2 1 3
95
,
3
155
,
3
7
,
14
10
,
5
E
2,1 10
1
1
5
3 3 1 2
155
,
3
0
,
25
95
,
3
85
,
3
10
.
5
E
2,1 10
•Удельная потенциальная энергия упругой деформации равна:
u
1 1 2 2
2
2
9666,95 10 5
3 3
2
МДж
.
3
м
95,3 63,87 10 5 ( 155,3) ( 85,3 10 5 )
2
2

14.

• Относительное изменение объема в окрестности рассматриваемой точки
будет:
1 2 3 63,87 10 5 7,14 10 5 85,3 10 5 14,25 10 5 ,
знак «-» показывает, что объем элемента уменьшается.
•Проверяем прочность материала:
- по 3-й теории прочности:
экв 1 3 95,3 ( 155,3) 250,3 МПа;
3
- по 4-й теории прочности:
экв4 12 22 1 2 2 3 3 1 95,33 155,3 2 95,3 155,3
219,09 МПа.
Прочность материала по 3-й и 4-й теориям прочности не удовлетворяет
условиям прочности, так как допускаемое напряжение для материала
элемента конструкции равно =180 МПа.

15.

Задача 4
На вал (рис., а) кольцевого сечения с радиусами R=10 см и r =8 см
действуют
две пары сил противоположного
направления с
моментами m=50 кН м на площадках, перпендикулярных к оси стержня.
Требуется:
•Построить эпюру крутящих моментов Мк;
•Определить касательные напряжения в поперечном сечении вала от
действия крутящего момента;
•Определить положение главных площадок и действующие на них главные
напряжения;
•Проверить условие прочности по 1-й и 2-й теориям прочности, если
р=60 МПа, = 0,15;
•Показать направление возможного раскрытия трещин.
а)
m
б)
1
t
r
R
1
L
m

16.

Решение:
1.Из условия равновесия отсеченной части вала определяем крутящий
а)
б)
m
момент и строим эпюру :
1
а)
б)
m
z
M к m 0;
M к m 50 кН м.
m
1
r
r
1
1
m
m
L
L
2.
Максимальные
касательные
напряжения в трубе от действия
Эпюра М кр
+
Эпюра
М кр
+
крутящего момента определяем по:
М кр max M кр
M кр 2
50 10 3 2
г)
д)
г)
д) МПа.
53
,
94
m
4
3 1 10 6 1
m
I
W
R 3 1 4
3,14 10
0
3,8
1
3
Так как в поперечном сечении вала возникают только касательные
напряжения, то вал испытывает деформацию чистого сдвига.
3
1
3.Положение главных площадок на наружной
площадке трубы
определяем
3
1
по:
2
tg 2 0
xy
x y
2
, отсюда 0 450
0 0
R
R

17.

Величины главных напряжений определяем по:
max
min
x y
2
1
2
x
y
2
+
2
4 xy
г)
53,94 МПа;
1
1 53,94 МПа,
3 53,94 МПа
3
3
1
4. Проверяем прочность вала по 1-й теории прочности, наибольшее
растягивающее напряжение не должно превышать допускаемое напряжение
при растяжении:
экв 1 53,94 p 60 МПа,
1
следовательно, по 1-й теории прочности материал
вала удовлетворяет условиям прочности.

18.

)
Проверяем прочность вала по 2-й теории прочности, наибольшая
растягивающая
деформация не должно
линейную
б) превышать допускаемую
в)
m
1
деформацию:
1
экв
1 2 3 53,94 0,15
R 53,94 62,03 МПа р
r
2
t
следовательно,
по 2-й теорииm прочности материал вала не удовлетворяет
1
L
условиям прочности.
5. Трещины в вале появятся от действия растягивающих напряжений 1,
следовательно,
направленияЭпюра
трещин
М кр будут перпендикулярными к
+
направлению 1 т.е. под углом 450 к оси вала.
)
д)
1
3
m
3
z
1
m