Похожие презентации:
Напряженное и деформированное состояния в точке
1.
Напряженное и деформированноесостояния в точке
2.
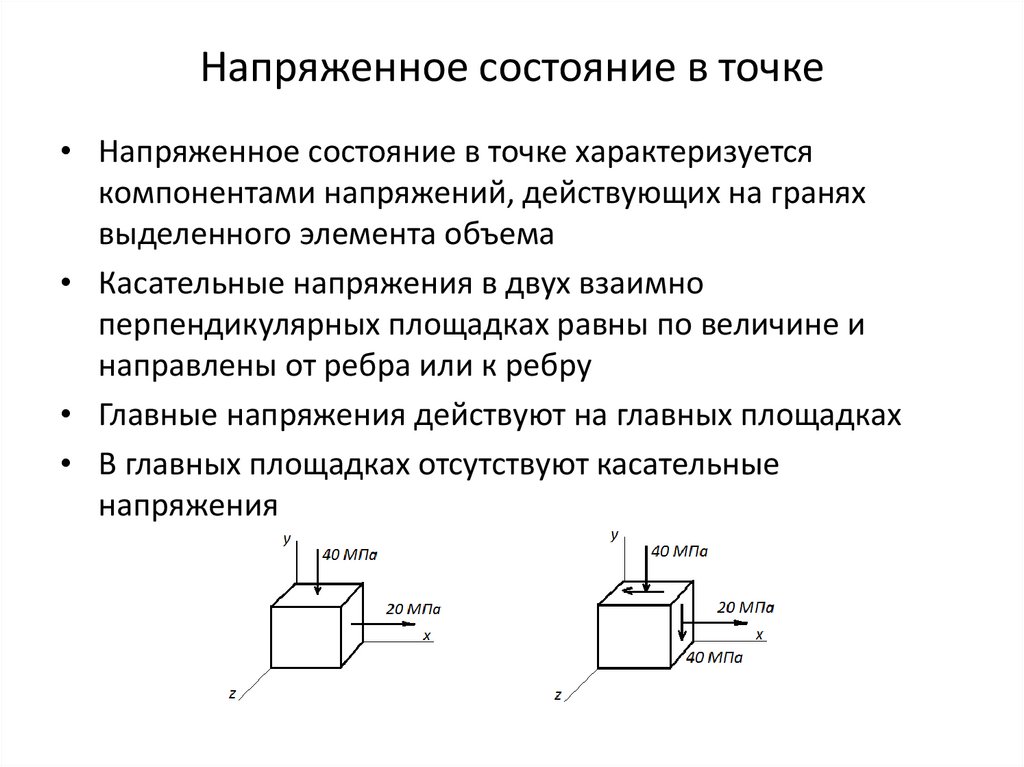
Напряженное состояние в точкеНапряженное состояние в точке
Виды напряженного состояния
Главные площадки и главные напряжения
Плоское напряженное состояние
Круги напряжений
3.
Напряженное состояние в точке• Напряженное состояние в точке характеризуется
компонентами напряжений, действующих на гранях
выделенного элемента объема
• Касательные напряжения в двух взаимно
перпендикулярных площадках равны по величине и
направлены от ребра или к ребру
• Главные напряжения действуют на главных площадках
• В главных площадках отсутствуют касательные
напряжения
4.
Виды напряженного состояния• Одноосное (линейное)
растяжение
сжатие
Двухосное (плоское)
Трехосное (объемное)
5.
Двухосное напряженное состояние в точкеНапряжения в наклонных площадках
max x
n
max min
2
nt
min y
max min
2
max min
2
cos 2
sin 2
6.
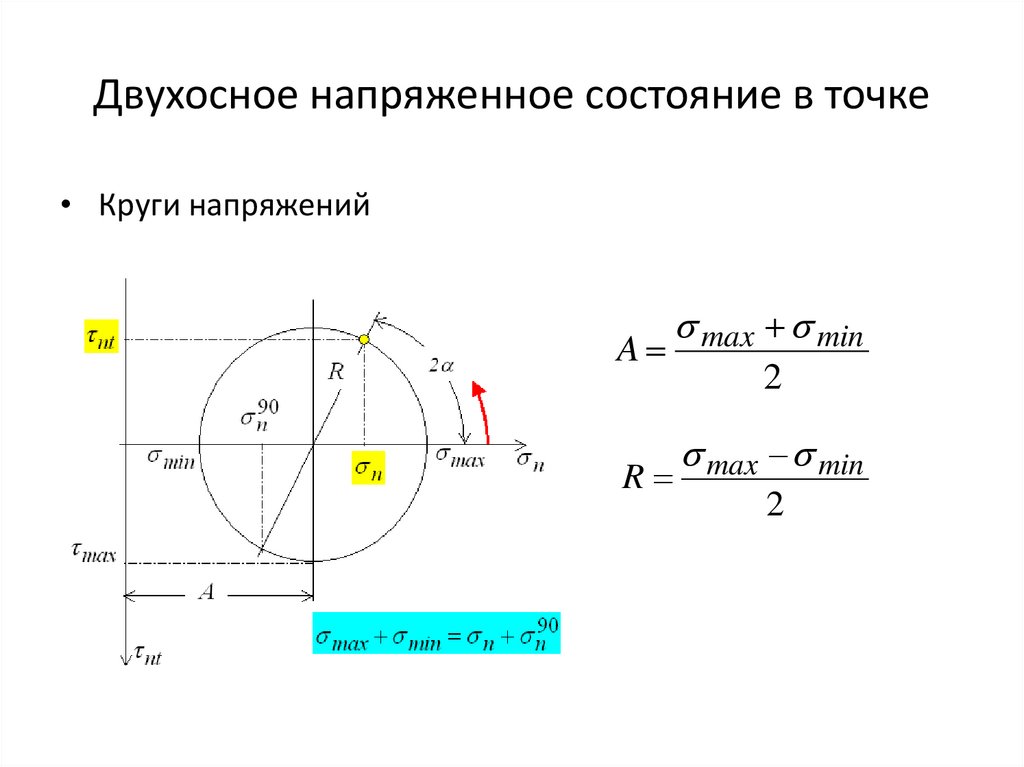
Двухосное напряженное состояние в точке• Круги напряжений
A
max min
R
max min
2
2
7.
Напряженное состояние в точке• Вычисление главных напряжений
max min
x y
2
2
x y
2
xy
2
• Определение положения главных площадок
tan 2
2 xy
x y
8.
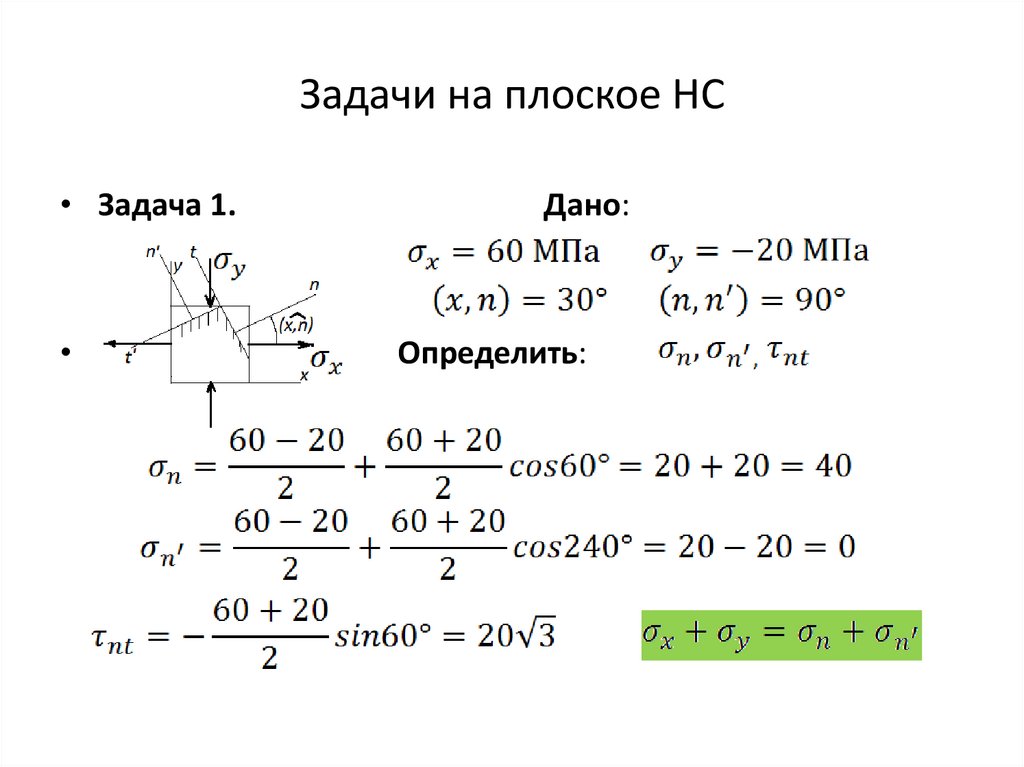
Задачи на плоское НС• Задача 1.
Дано:
Определить:
9.
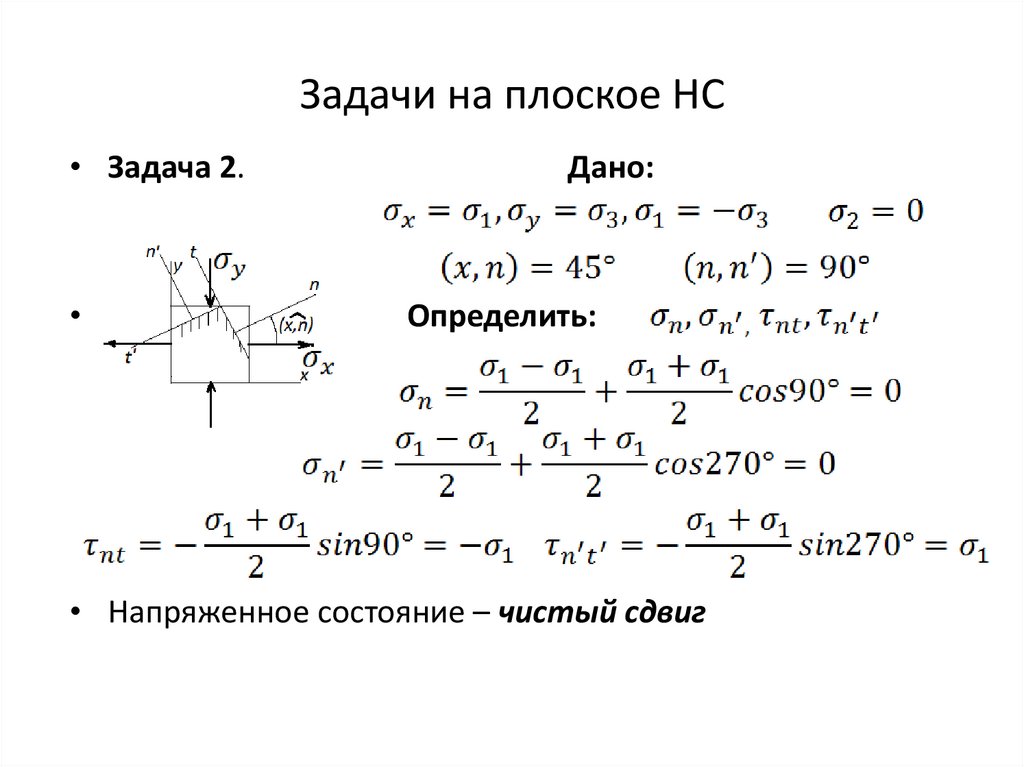
Задачи на плоское НС• Задача 2.
Дано:
Определить:
• Напряженное состояние – чистый сдвиг
10.
Объемное напряженное состояние• Задача 3.
Дано:
Определить:
- главное напряжение, остальные два
находятся в плоскости х-у и определяются по формулам
для плоского напряженного состояния
Тогда
,
,
11.
Напряженно-деформированное состояние вточке
• Обобщенный закон Гука
1
1 2 3
E
1
2 2 3 1
E
1
3 3 1 2
E
1
;
1
x x y z
E
1
y y z x
E
1
z z x y
E
xy
;
xy
G
;
xz xz ;
G
;
yz
yz
G
.
12.
Напряженно-деформированное состояние вточке. Уравнения упругости
• Относительное изменение объема
V x y z
1 2
1 2
1 2 3
V
x y z
E
E
• Удельная потенциальная энергия деформации
1 2
a
1 22 32 2 1 2 1 3 2 3
2E
• Удельная потенциальная энергия изменения объема и
формы
1 2
1 2 3 2
a0
6E
1
1 2 2 1 3 2 2 3 2
aф
6E
13.
Напряженно-деформированное состояние вточке
• Задача 4. Объемное напряженное состояние в точке
задано главными напряжениями:
,
. Определить относительные деформации
если угол
в плоскости x-y,
Е=2·10^5 МПа, μ=0,3.
Решение:
,
14.
Напряженно-деформированное состояние вточке
• Задача 5. Кубик со стороной 2 см находится под
действием касательного напряжения
МПа.
Определить: на сколько изменится диагональ
АВ, если Е=1·10^5, μ=0,3.
Решение: 1. НС – чистый сдвиг.
15.
Напряженно-деформированное состояние вточке
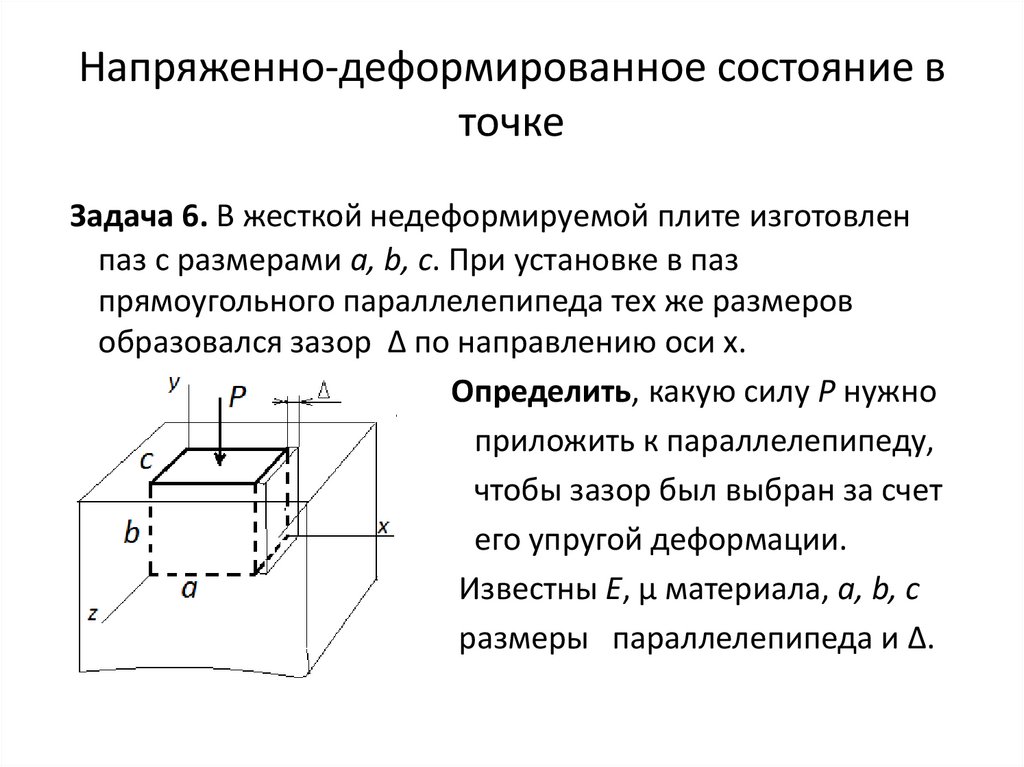
Задача 6. В жесткой недеформируемой плите изготовлен
паз с размерами a, b, c. При установке в паз
прямоугольного параллелепипеда тех же размеров
образовался зазор Δ по направлению оси х.
Определить, какую силу Р нужно
приложить к параллелепипеду,
чтобы зазор был выбран за счет
его упругой деформации.
Известны Е, μ материала, a, b, c
размеры параллелепипеда и Δ.
16.
Напряженно-деформированное состояние вточке (продолжение)
Посмотрим, что известно.
17.
Напряженно-деформированное состояние вточке (продолжение)
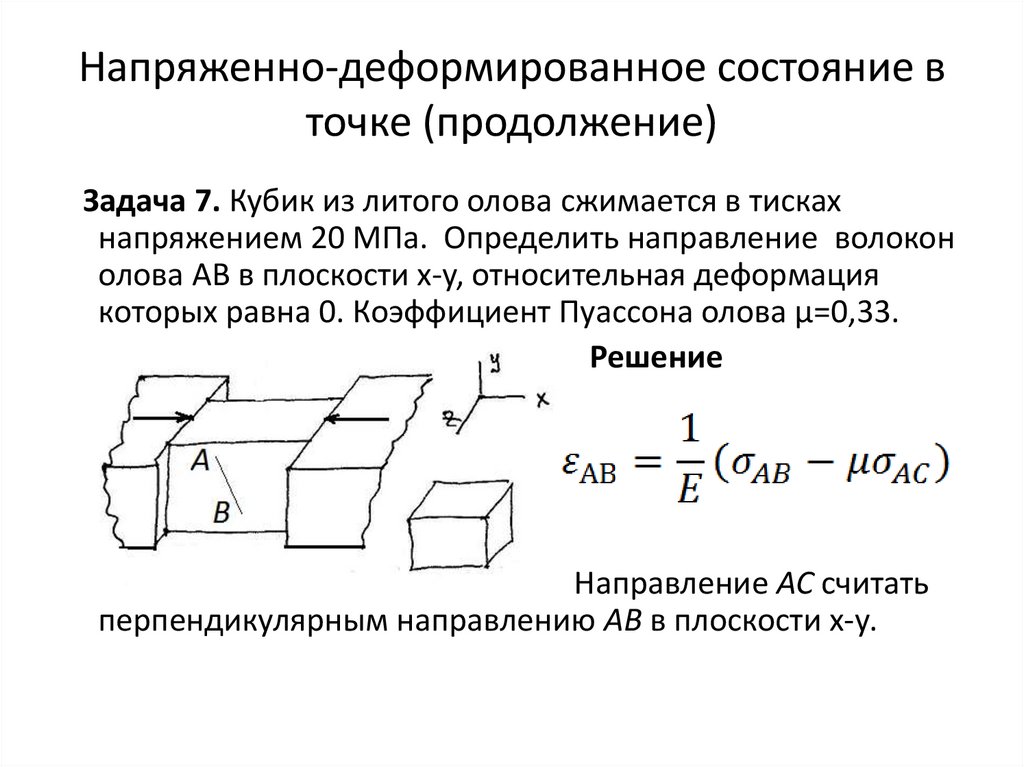
Задача 7. Кубик из литого олова сжимается в тисках
напряжением 20 МПа. Определить направление волокон
олова АВ в плоскости x-y, относительная деформация
которых равна 0. Коэффициент Пуассона олова μ=0,33.
Решение
Направление АС считать
перпендикулярным направлению АВ в плоскости х-у.
18.
Напряженно-деформированное состояние вточке (продолжение)
19.
Напряженно-деформированное состояние вточке (продолжение)
20.
Напряженно-деформированное состояние вточке (продолжение)
• Задача 8. В каком случае объемная деформация стержня,
нагруженного одинаковой продольной силой, будет
больше, когда стержень свободно стоит на опоре, или,
когда он предварительно заключен в жесткую
недеформируемую обойму?
• Ответ на этот вопрос дает анализ формулы объемной
деформации:
1 2
1 2
1 2 3
V
x y z
E
E














 Механика
Механика








