Множественный регрессионный анализ

1. Множественный регрессионный анализ

Обозначения:
x1, x2 , ..., xk
y - отклик y x1, x2 ,..., xk
- модель
- факторы
y набл x1 , x2 , ..., xk
МНК – метод наименьших квадратов
yнабл у мод
2
Требования:
1) M i 0
2) D i
min
3) M i j 0
2
4) i ~ N 0,
i j
i 1, n
1

2. Множественная линейная регрессия

y b0 b1x1 b2 x2 ... bk xk
- линейная модель
yi - i-ое наблюдаемое значение отклика
- i-ые наблюдаемые
xi1, xi 2 , ..., xik
значения факторов
i 1, n
yi b0 b1xi1 b2 xi 2 ... bk xik i
МНК:
2
i min
2

3. Множественная линейная регрессия

Модель: y b0 b1x1 b2 x2 ... bk xk
x0 1 y b x b x b x ... b x
0 0
11
2 2
k k
Наблюдения:
i 1, n
yi b0 xi 0 b1xi1 b2 xi 2 ... bk xik i
y1
x10 x11
y2
x20 x21
y X
...
...
...
y
x
n
n0 xn1
n 1
... x1k
b0
1
... x2k
b1
2
b
...
...
... ...
b
... xnk
n
k
n k 1
k 1 1
n 1

4. Множественная линейная регрессия

y Xb
Q b
2
Т
i
2
i min
МНК:
1 2 ... n
y Xb
Т
Т
y Xb y Xb
Т
Т
Т Т
y b X y Xb
Т
Т Т
Т
Т Т
y y b X y y Xb b X Xb
4

5. Множественная линейная регрессия

y Xb
Q b
2
i
2
i min
МНК:
Т
Т Т
Т
Т Т
y y b X y y Xb b X Xb
bQ b X Т y X Т y X Т Xb X Т Xb 0
Т
Т
X Xb X y
Т
с с
с
b с
,
,...,
b0 b1 bk
Т 1 Т
b X X X y
b bT A A b Ab AT
T
T
b b Ab Ab A b

6. Множественная линейная регрессия

Т
Т
X Xb X y
1 1
x11 x21
T
X X
... ...
x x
1k 2 k
n
xi1
T
X X
...
x
ik
- система нормальных уравнений
...
...
...
...
1 1
xn1 1
... ...
xnk 1
xi1
2
xi1
...
...
...
...
xi1xik ...
x11
x21
...
xn1
...
...
...
...
x1k
x2 k
...
xnk
xik
xi1xik
...
2
x
ik

7. Множественная линейная регрессия

Т
Т
X Xb X y
n
xi1
T
X Xb
...
x
ik
1 1
x11 x21
T
X Y
... ...
x x
1k 2 k
xi1
2
xi1
Т 1 Т
b X X X y
...
...
...
...
xi1xik ...
...
...
...
...
xik b0
xi1xik b1
...
2
xik
...
b
k
1 y1 yi
xn1 y2 xi1 yi
...
...
...
xnk yn xik yi

8. Множественная линейная регрессия

Т
Т
Т 1 Т
b X X X y
X Xb X y
y b0 b1x1 b2 x2
nb
b1 xi1 b2 xi 2 yi
0
2
b0 xi1 b1 xi1 b2 xi1xi 2 xi1 yi
b x b x x b x 2
0 i 2 1 i1 i 2 2 i 2 xi 2 yi

9. Интервальные оценки

Т 1 Т
b X X X y
y Xb
Оценка остаточной
дисперсии
2
S
n
1
n k 1
S
2
n k 1
2
yi b0 b1xi1 ... bk xik
i 1
bi bi t табл sb i
tтабл t
;
n
k
1
2
Q b
sb i s cii
Т
С X X
i 1, n
1

10. Множественная линейная регрессия

y Xb
Адекватность модели
Оценка остаточной
дисперсии
n
1
n k 1
i 1
Оценка общей
дисперсии
2
S
H 0 : D y D
H1 : D y D
S
Q b
2
n k 1
2
yi b0 b1xi1 ... bk xik
2
Sy
n
yi y
n 1
1
2
i 1
2
Sy
~ F n 1;n k 1
2
S
10

11. Полиномиальная регрессия

2
3
k
y b0 b1x b2 x b3 x ... bk x
k
2
Замена: x x1 x x
x
x
k
2
...
y b0 b1x1 b2 x2 ... bk xk
x0 1 y b0 x0 b1x1 b2 x2 ... bk xk
В матричной y
y
X
b
X
b
форме
набл
мод
МНК:
2
i min
Т 1 Т
b X X X y
11

12. Полиномиальная регрессия

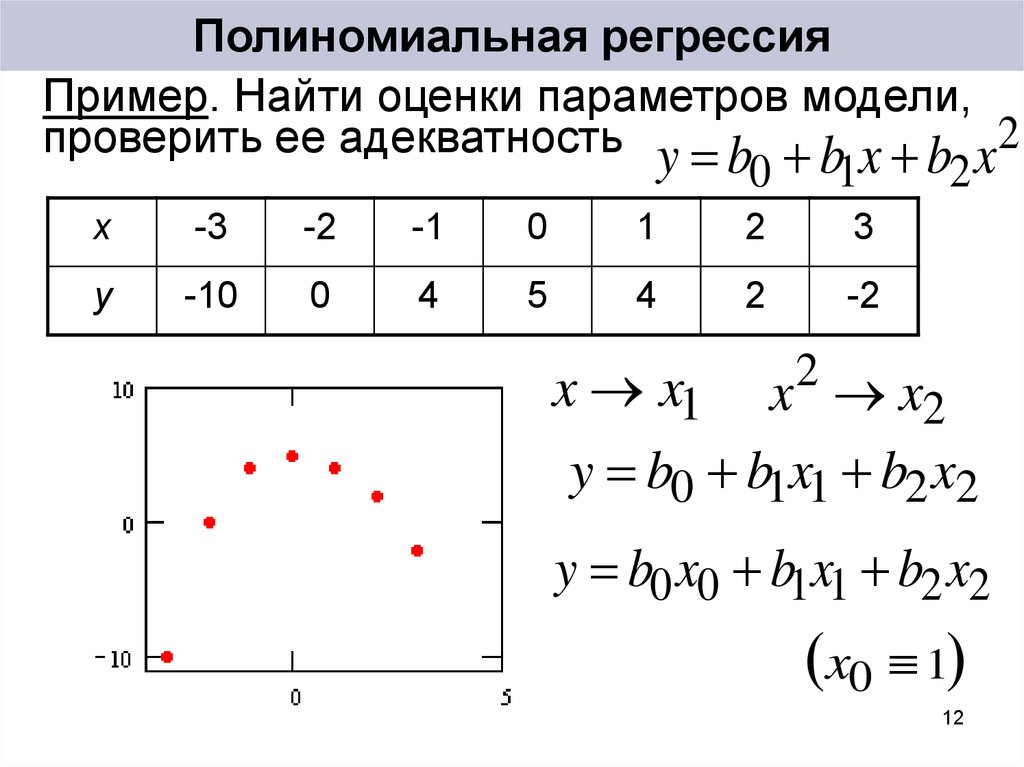
Пример. Найти оценки параметров модели,
проверить ее адекватность y b b x b x 2
0 1
2
x
-3
-2
-1
0
1
2
3
y
-10
0
4
5
4
2
-2
x x1 x x2
y b0 b1x1 b2 x2
2
y b0 x0 b1x1 b2 x2
x0 1
12

13.

Пример
(продолжение).
x
-3
-2
-1
0
1
2
3
y
-10
0
4
5
4
2
-2
Перейдем к
матричной форме
y b0 x0 b1x1 b2 x2
1 3 9
10
1 2 4
0
1 1 1
4
y 5
X 1 0 0
4
1 1 1
2
1 2 4
2
1 3 9
y Xb
Т 1 Т
b X X X y
0 28
7
T
X X 0 28 0
28 0 196
13

14.

0 28
7
1
T
X X 0 28 0 С X Т X
28 0 196
0.33 0 0.05
1
Т
Т
С 0 0.04 0
b X X X y
0.05 0 0.01
Пример
(продолжение).
5.38
b 1
1.24
y b0 b1x b2 x 2
y 5.38 x 1.24 x
2

15.

Интервальные оценки
2
b 5.38
y 5.38 x 1.24 x
Пример
(продолжение)
bi bi t табл sb i
sb0 2.78 1.3 0.33
b0 3.29; 7.47
sb1 2.78 1.3 0.04
b1 0.31;1.69
sb2 2.78 1.3 0.01
b2 1.64 ; 0.84
1.24
1
Т
0.33 0 0.05
С 0 0.04 0
0.05 0 0.01
S
2
2
S
Q b
n k 1
6,78
7 3
S 2 1.695
S 1 .3
t табл 2.78
0.05 4

16.

Пример
(продолжение)
Адекватность модели
2
Q
b
2
y 5.38 x 1.24 x
S
H 0 : D y D
H1 : D y D
2
Sy
2
S
n
yi y
n 1
1
n k 1
2
i 1
2
Sy
~ F n 1;n k 1
2
S
Вывод: модель адекватна
6,78
7 3
2
S 1.695
2 163.71
Sy
27.285
7 1
Fнабл 16.09
Fтабл 6.16
16