Повторение курса геометрии

1.

Повторение курса
геометрии

2. Равносторонний треугольник

С
a2 3
S
4
a 3
h
2
a
R
3
r
a
2 3

3. Равнобедренный треугольник

В
АВ=ВС
A B
m
h
hс= mс=lс
l
А
С
M

4. Теорема Пифагора

В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов:
c a b
2
В
2
c
а
С
2
b
А
a
sin ;
c
b
сos ;
c
tg
a
b

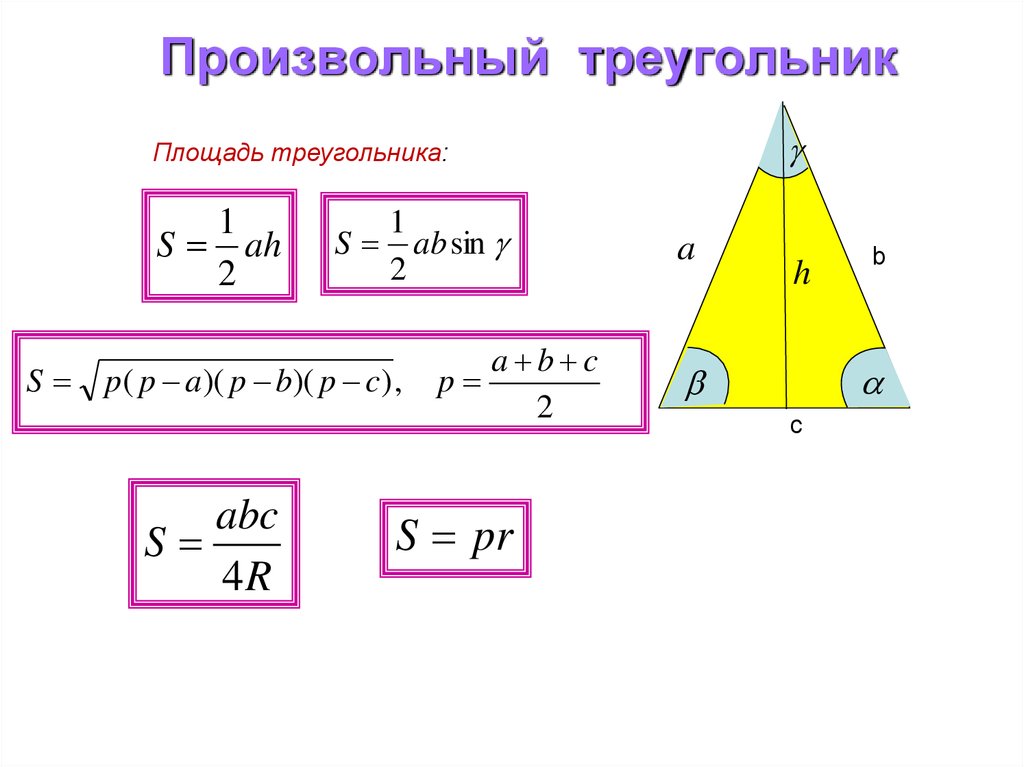
5. Произвольный треугольник

Площадь треугольника:
1
S ah
2
S
S
1
ab sin
2
p( p a)( p b)( p c) ,
abc
S
4R
p
a b c
2
S pr
a
h
b
c

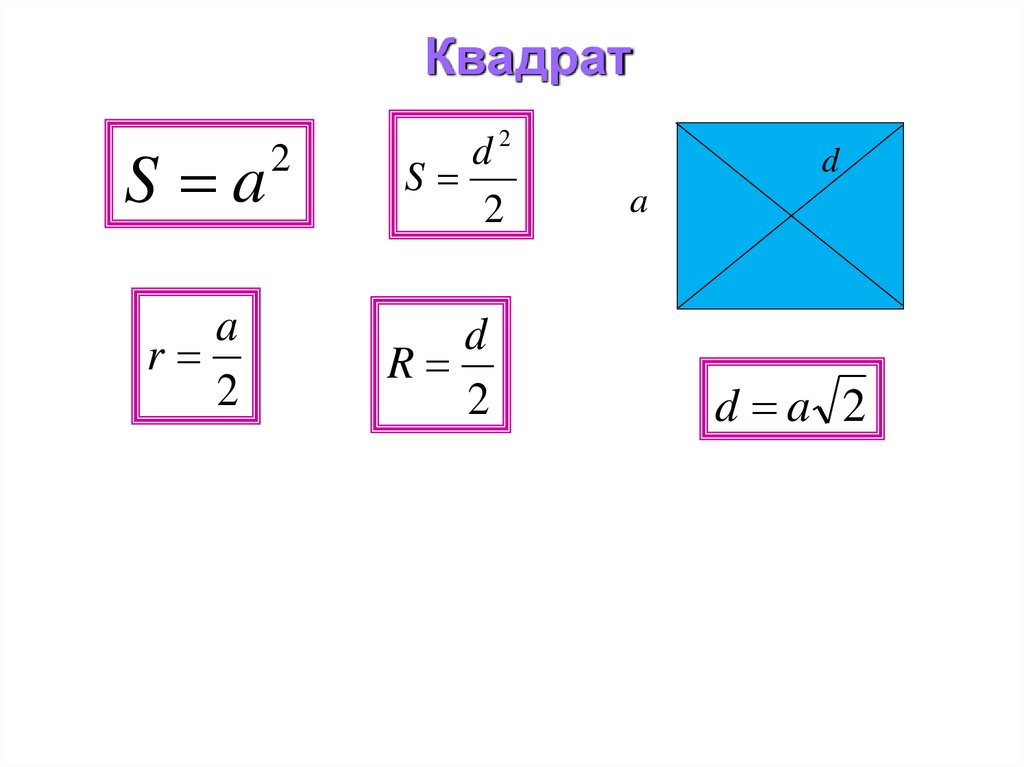
6. Квадрат

S a
a
r
2
2
2
d
S
2
d
R
2
d
a
d a 2

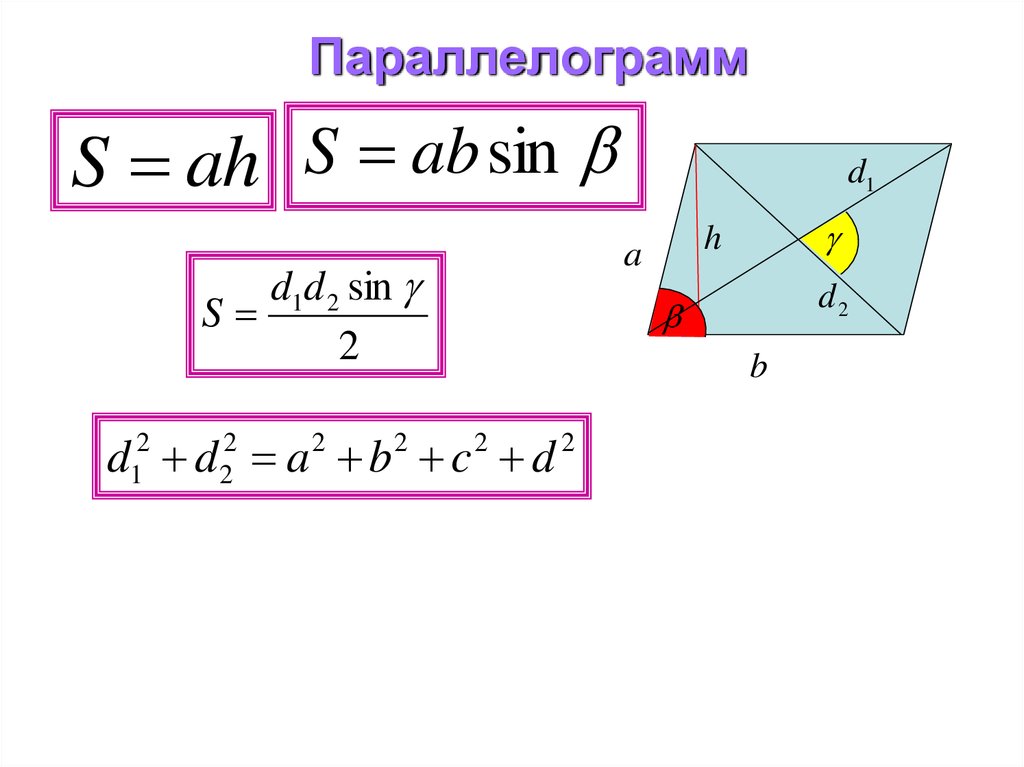
7. Параллелограмм

S ah S ab sin
d1d 2 sin
S
2
d12 d 22 a 2 b 2 c 2 d 2
d1
h
a
d2
b

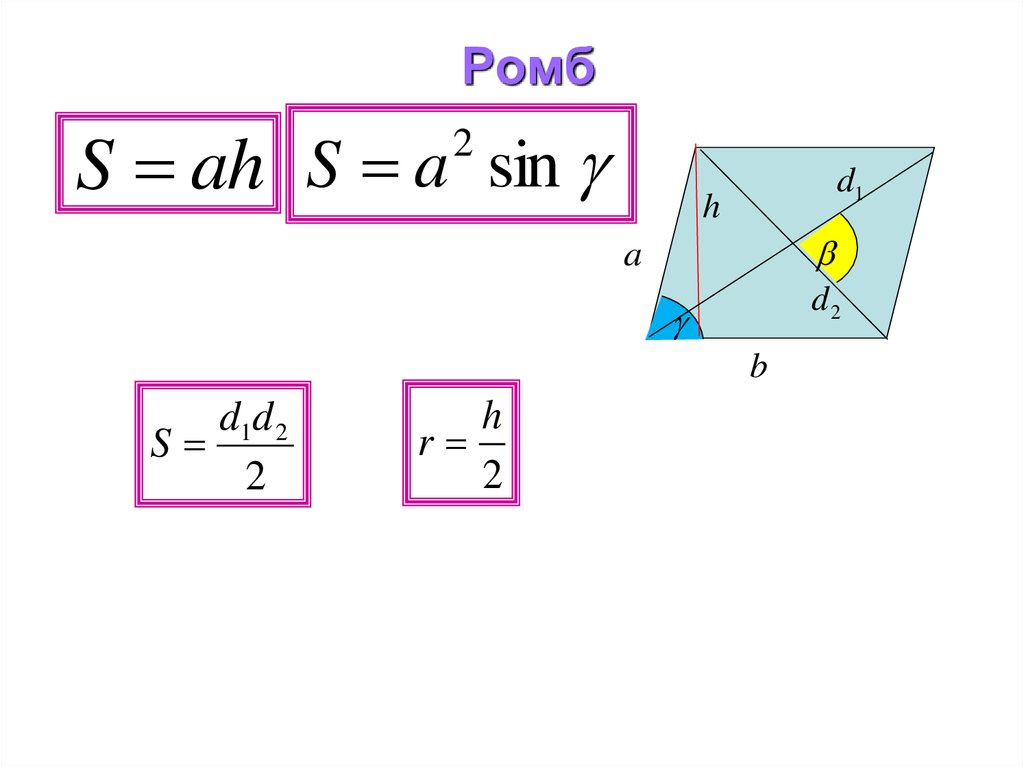
8. Ромб

S ah S a sin
2
d1
h
d2
a
b
d1d 2
S
2
h
r
2

9. Трапеция

a b
d1d 2 sin
S
h S
2
2
a b
MN
2
M
b
d1
h
N
d2
a

10.

11.

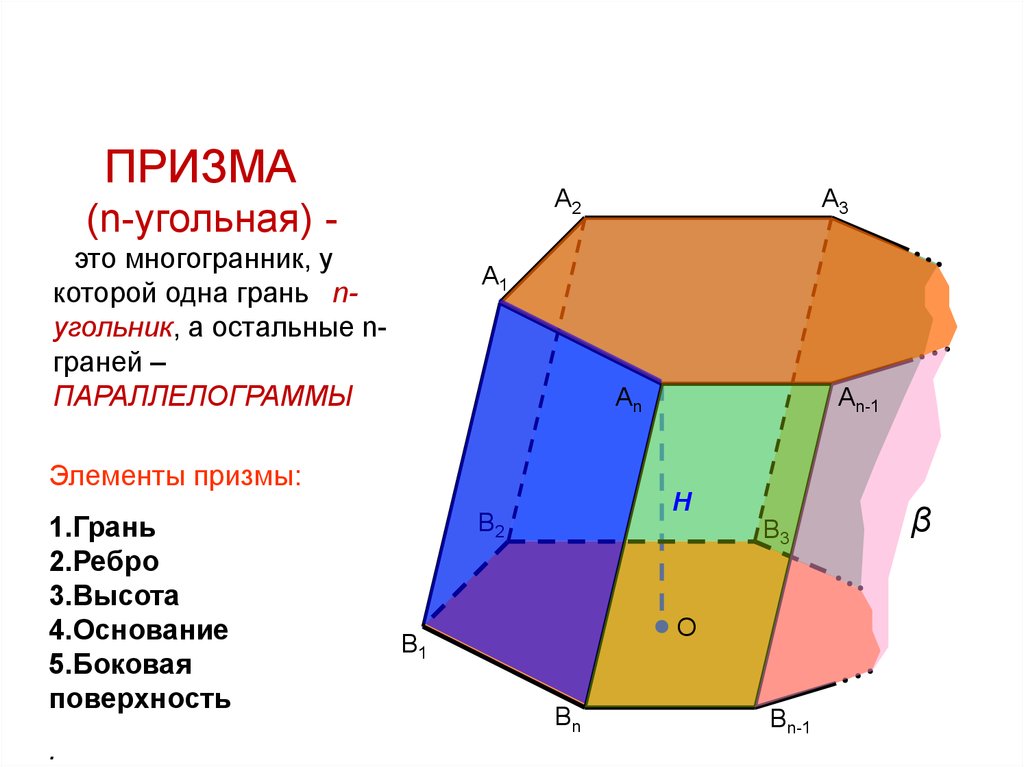
ПРИЗМА
A2
(n-угольная) это многогранник, у
которой одна грань nугольник, а остальные nграней –
ПАРАЛЛЕЛОГРАММЫ
A3
A1
An
An-1
Элементы призмы:
1.Грань
2.Ребро
3.Высота
4.Основание
5.Боковая
поверхность
.
H
B2
B3
O
B1
Bn
Bn-1
β

12.

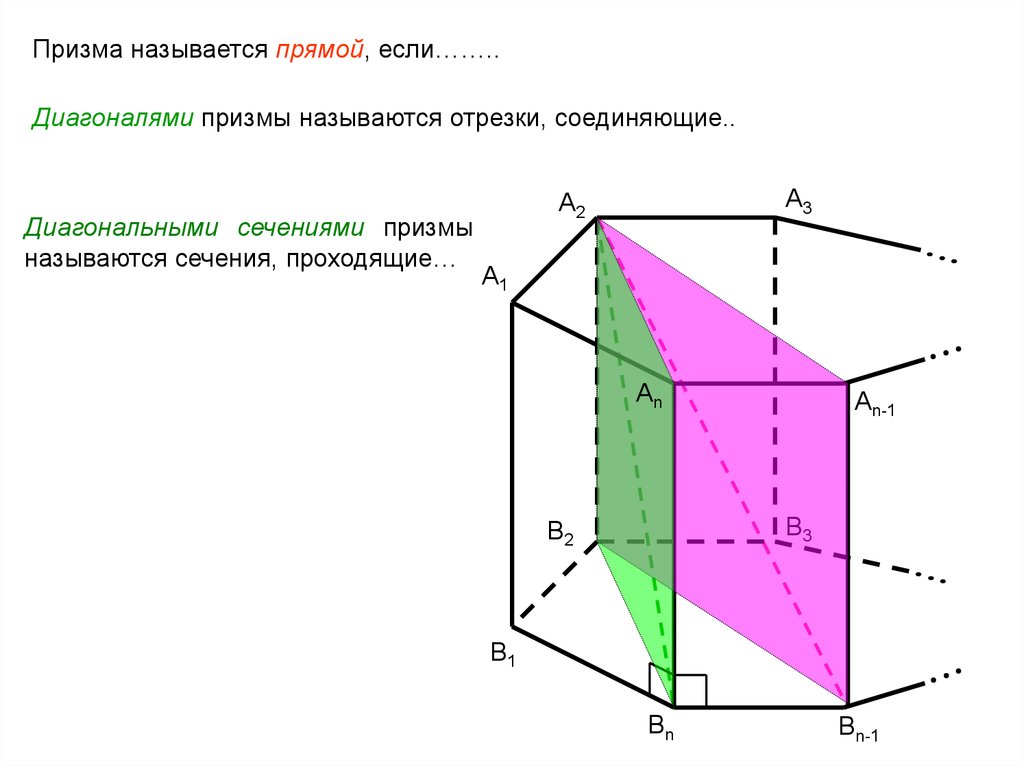
Призма называется прямой, если……..
Диагоналями призмы называются отрезки, соединяющие..
Диагональными сечениями призмы
называются сечения, проходящие…
A3
A2
A1
An
An-1
B3
B2
B1
Bn
Bn-1

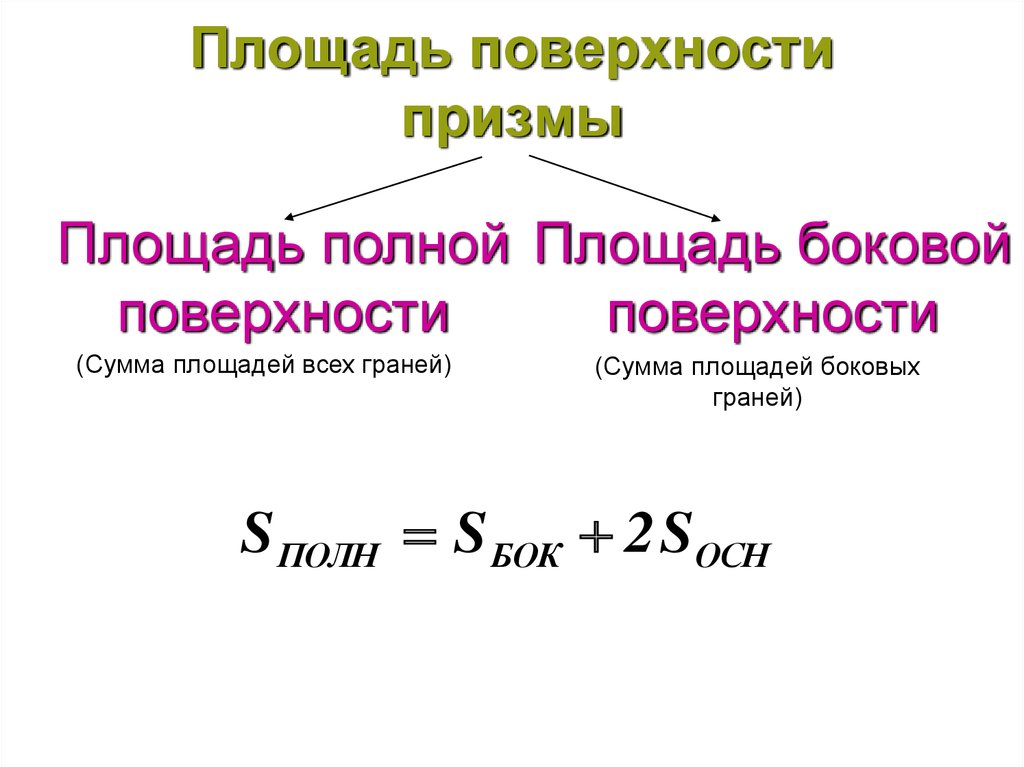
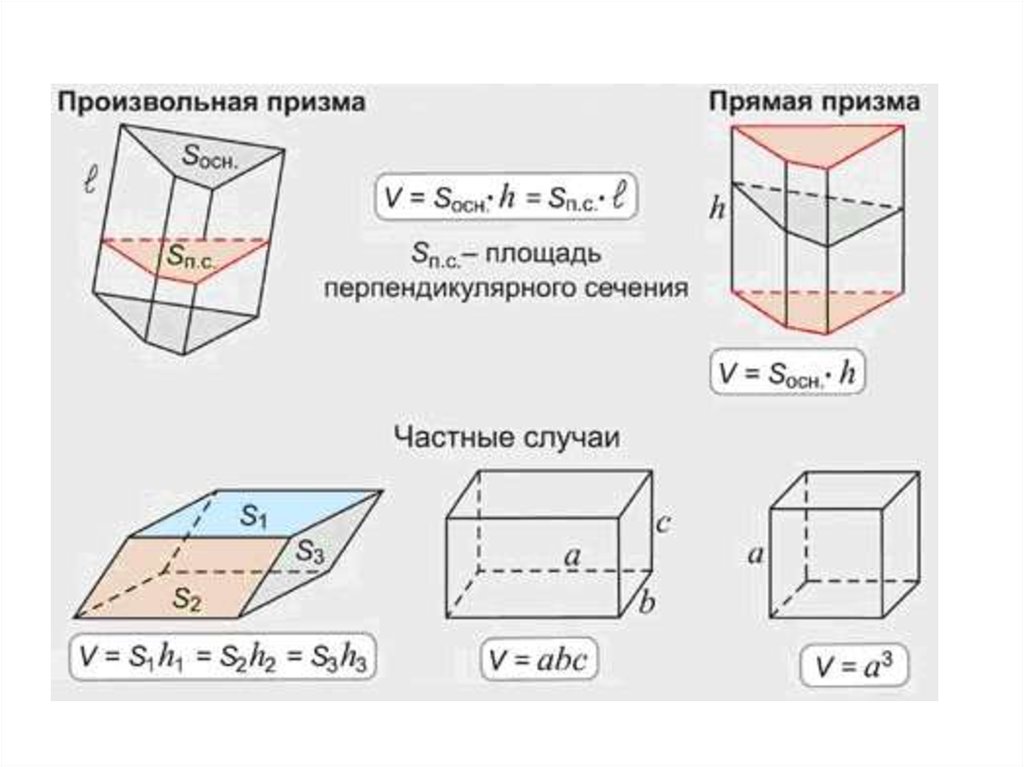
13. Площадь поверхности призмы

Площадь полной Площадь боковой
поверхности
поверхности
(Сумма площадей всех граней)
(Сумма площадей боковых
граней)
S ПОЛН S БОК 2 SОСН

14. Площадь боковой поверхности призмы

Sбок Pосн h
Sбок Pсеч l
Bn
B3
B2
B1
A3
An
A2
A1

15.

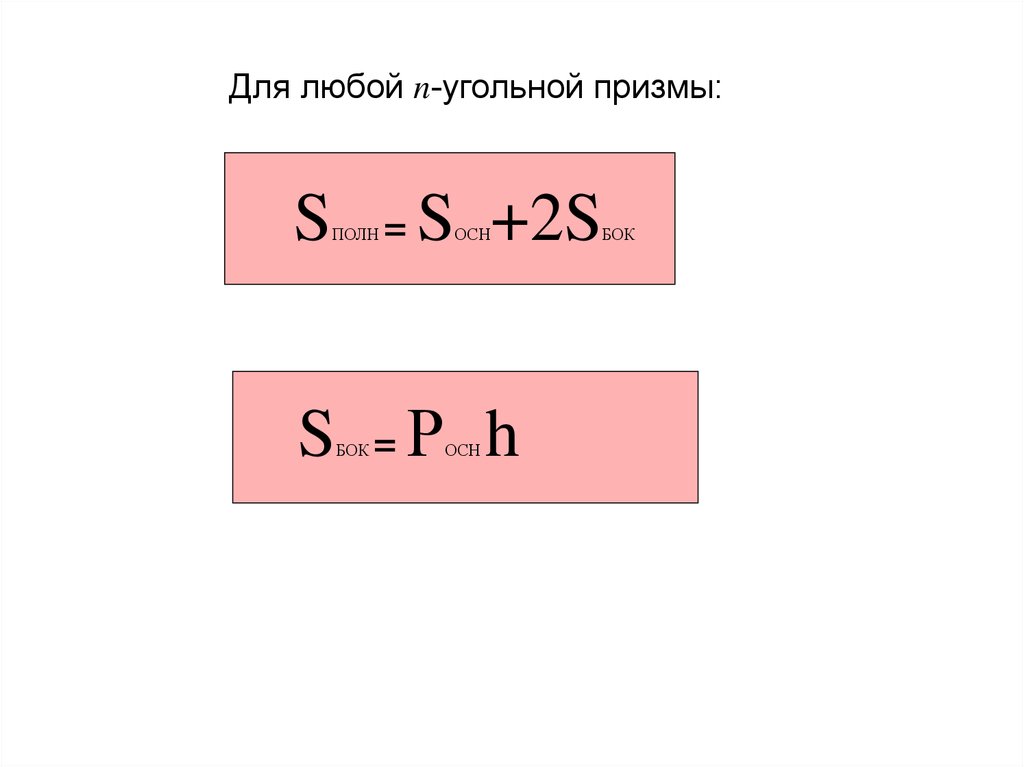
Для любой n-угольной призмы:
S
=
S +2S
=
Р h
ПОЛН
S
БОК
ОСН
ОСН
БОК

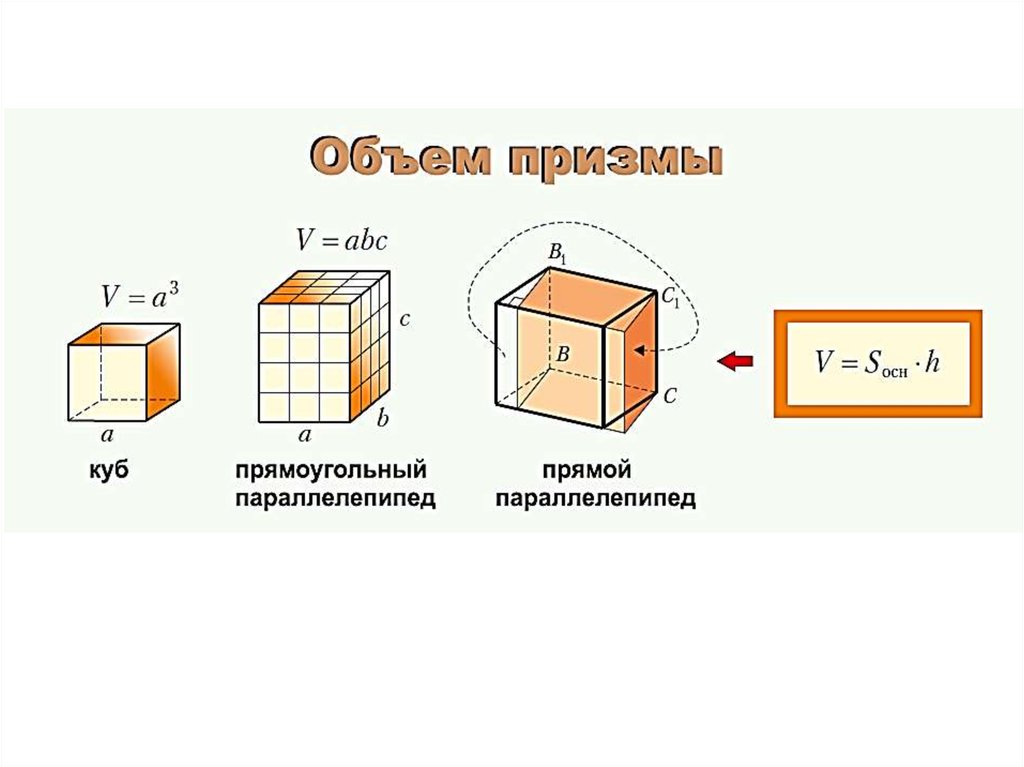
16.

Призма и параллелепипед

17.

18.

19.

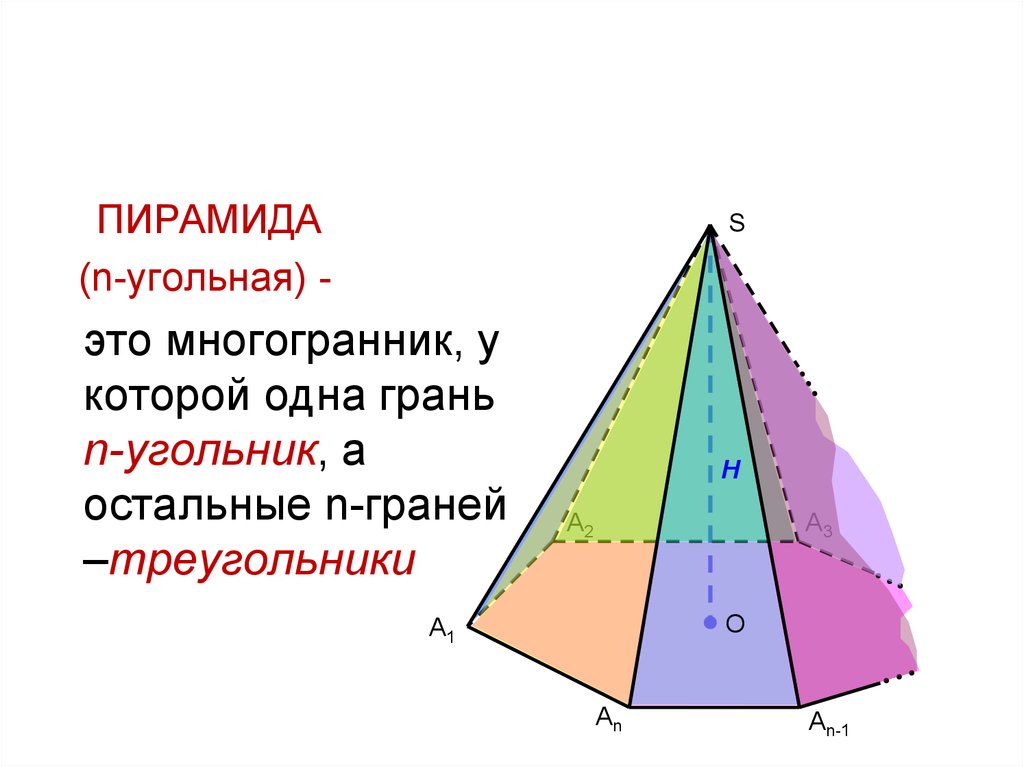
ПИРАМИДА
(n-угольная) -
S
это многогранник, у
которой одна грань
n-угольник, а
остальные n-граней
–треугольники
H
A2
A3
O
A1
An
An-1

20.

S
• ПРАВИЛЬНАЯ
ПИРАМИДА
(n-угольная) -
это пирамида,
основание которой
– правильный nугольник
а все боковые
ребра равны
между собой
A2
A3
A1
An
An-1

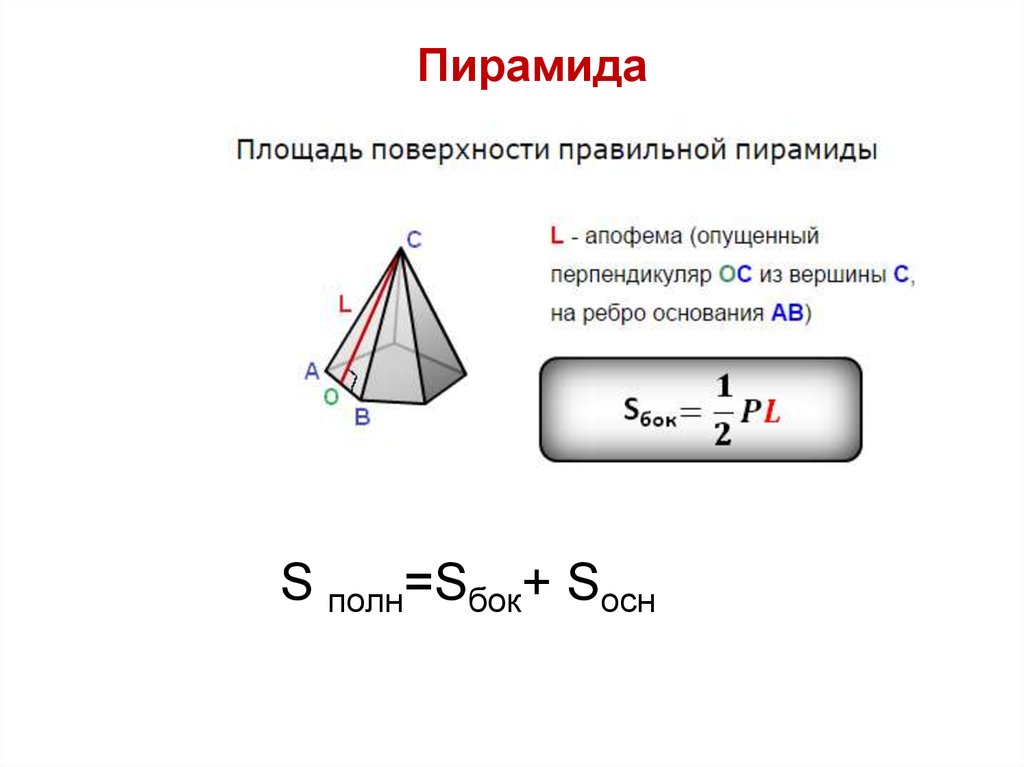
21. Площадь поверхности пирамиды

Площадь полной Площадь боковой
поверхности
поверхности
(Сумма площадей всех граней)
(Сумма площадей боковых
граней)
S ПОЛН S БОК SОСН

22.

Пирамида
S полн=Sбок+ Sосн

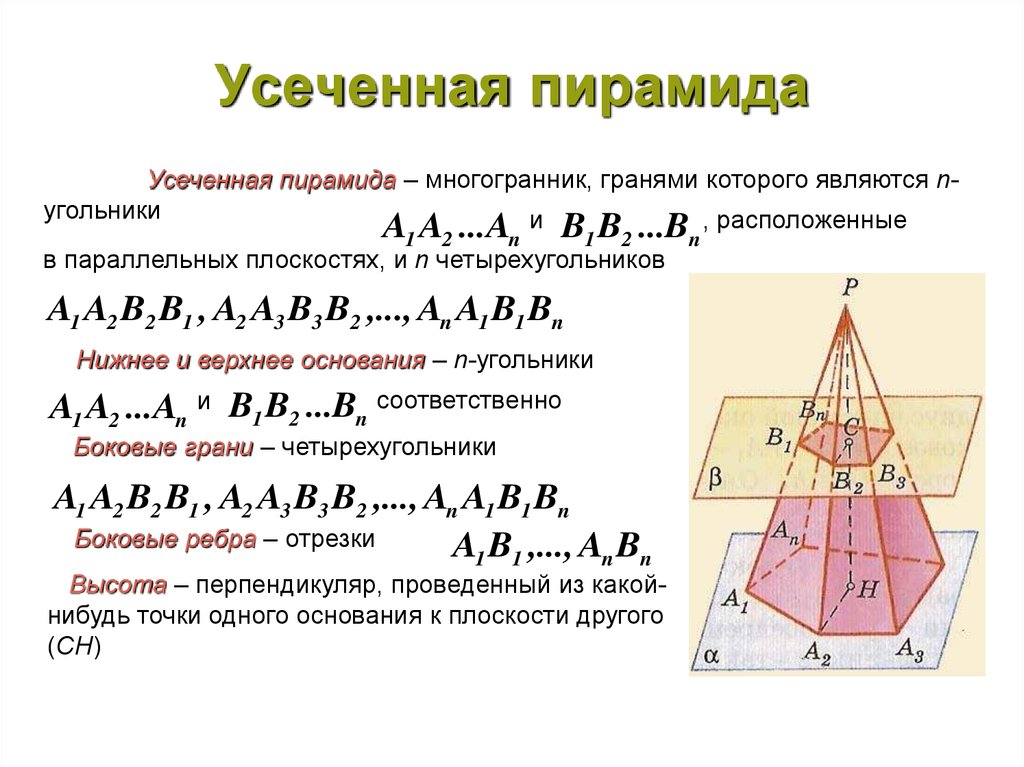
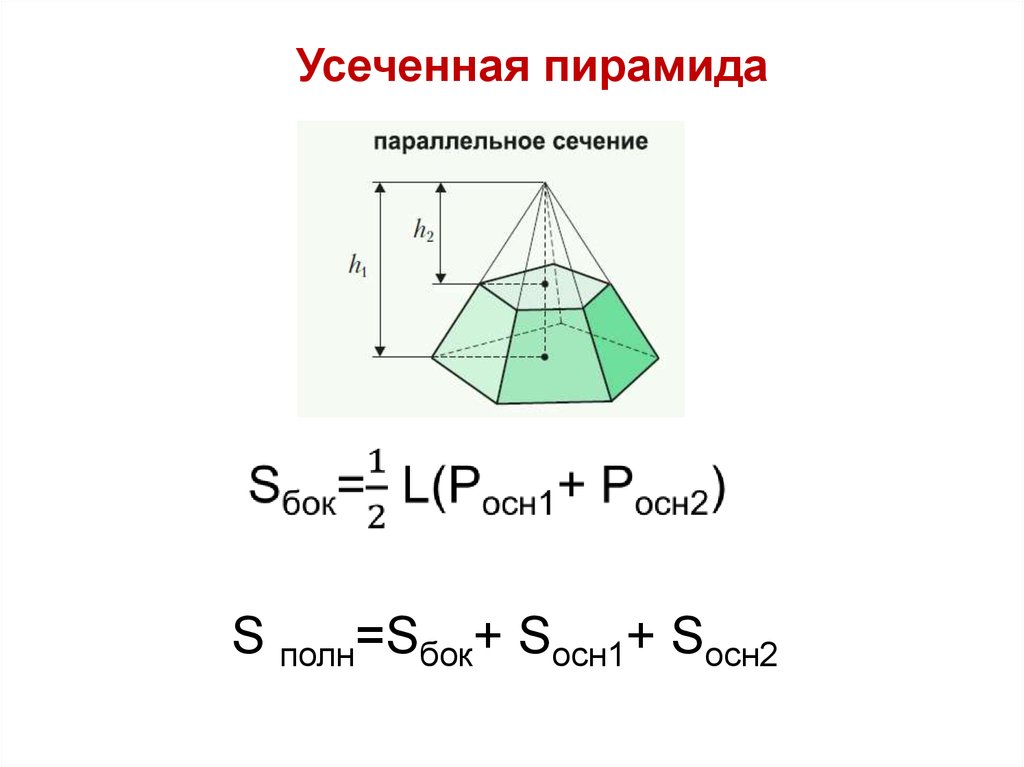
23. Усеченная пирамида

Усеченная пирамида – многогранник, гранями которого являются nугольники
и
, расположенные
A1 A2 ...An
B1 B2 ...Bn
в параллельных плоскостях, и n четырехугольников
A1 A2 B2 B1 , A2 A3 B3 B2 ,..., An A1 B1 Bn
Нижнее и верхнее основания – n-угольники
A1 A2 ...An и B1 B2 ...Bn соответственно
Боковые грани – четырехугольники
A1 A2 B2 B1 , A2 A3 B3 B2 ,..., An A1 B1 Bn
Боковые ребра – отрезки
A1 B1 ,..., An Bn
Высота – перпендикуляр, проведенный из какойнибудь точки одного основания к плоскости другого
(CH)

24.

Усеченная пирамида
S полн=Sбок+ Sосн1+ Sосн2

25.

26.

Тела вращения

27.

Тела вращения

28.

Тела вращения