Векторы в пространстве

1. Векторы

План.
1. Векторное n – мерное пространство.
2. Пространство R2 и R3.
3. Скалярное произведение векторов. Длина
вектора. Угол между векторами.
4. Плоскость в трехмерном пространстве.
5. Прямая линия в трехмерном пространстве.
6. Линейная зависимость и линейная независимость
векторов. Базис пространства Rn.

2. Векторное n – мерное пространство.

Определение. Пусть n – любое
натуральное число. Упорядоченная
совокупность n чисел a1, a2, …, an
называется n – мерным вектором.
А
В

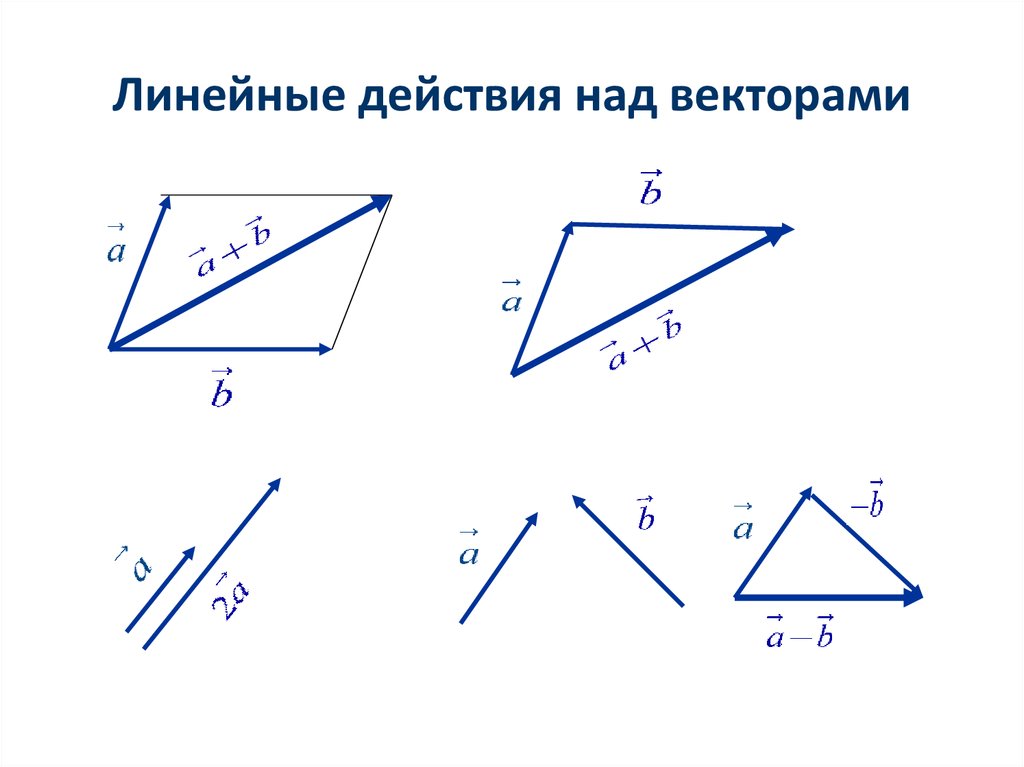
3. Линейные действия над векторами

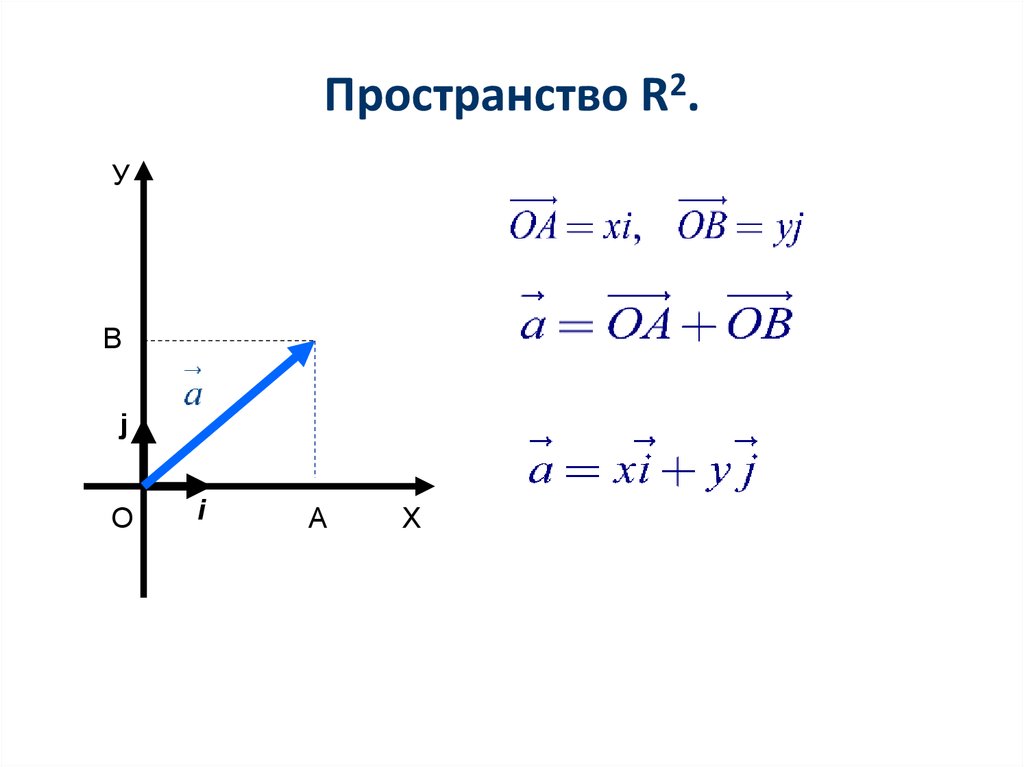
4. Пространство R2.

У
B
j
О
i
A
Х

5. Пространство R3.

Z
C
k
B
i
O
j
Y
A
X
К

6. Скалярное произведение векторов

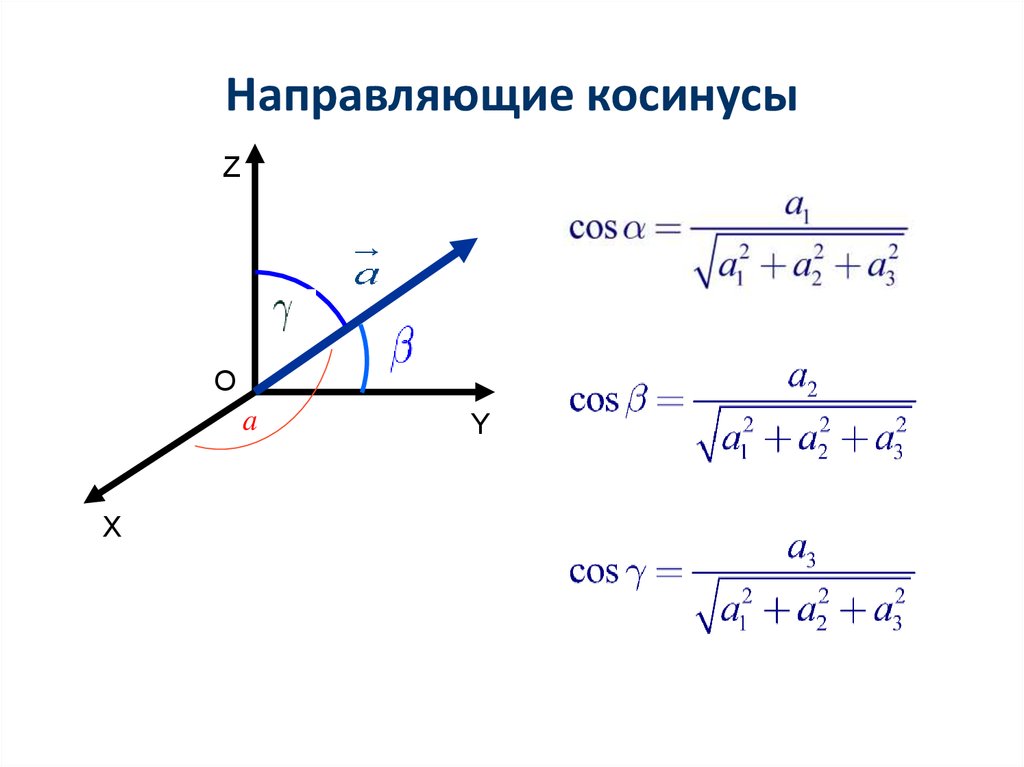
7. Направляющие косинусы

Z
О
a
X
Y

8. Векторное произведение векторов

9. Свойства векторного произведения

10. Смешанное произведение векторов

11. Свойства смешанного произведения

12. Поверхность в трехмерном пространстве

Z
f (x; y; z )= 0
Y
X

13. Плоскость в трехмерном пространстве

Z
M
N
O
Y
X
A(x - x0 )+ B (y - y0 )+ C (z - z0 )= 0
Ax + By + Cz + D = 0

14. Прямая линия в трехмерном пространстве

Z
N
М
N1
О
У
(x - x0 ; y - y0 ; z - z0 )= (t l; t m; t n)
Х
x x0 tl ;
y y0 tm; z z0 tn
x = x0 + t l , y = y0 + t m, z = z0 + t n

15. Прямая линия в трехмерном пространстве

x - x0
y - y0
z - z0
= t,
= t,
= t,
l
m
n
x - x0
y - y0 z - z0
=
=
l
m
n

16. Пример 2. Даны координаты точек А(–6; 0; 0), В(–1; 1; 0), С(–3; 5; 4). Требуется: 1) записать векторы в системе орт и найти

модули этих векторов;
2) найти угол между векторам;
3) составить уравнение плоскости, проходящей через точку С
перпендикулярного вектору .
Решение.
1) Координаты векторов
Следовательно,
Запишу векторы
в системе орт:

17.

Найду модули этих векторов по формулам
Получаем
2) Найдем угол между векторам

18.

Найдем скалярное произведение векторов
Тогда cos α равен
3) Составим уравнение плоскости, проходящей через точку
С(-3;5;4) перпендикулярного вектору
.
По формуле
Получаем

19. Контрольные вопросы

1) Метод координат. Расстояние между двумя точками.
2) Деление отрезка в данном отношении.
3) Уравнение прямой линии не плоскости. Угол между прямыми
линиями.
4) Кривая второго порядка. Эллипс. Гипербола. Парабола.
5) Полярная система координат.
6) Векторное n-мерное пространство.
7) Вектор. Действия над векторами. Свойства. Длина вектора.
8) Скалярное произведение. Свойства.
9) Угол между векторами.
10) Векторное произведение. Свойства.
11) Смешанное произведение . Свойства.
12) Линейная зависимость и линейная независимость векторов.
13) Плоскость в трехмерном пространстве.
14) Прямая линия в трехмерном пространстве.