Похожие презентации:
Основания математики. Элементы теории графов
1. Математика
Лекции – 2 часа
Практические занятия – 6 часов
Зачет с оценкой
Контрольная работа (домашняя) по методичке
15876 (с.27)
• Методические указания 14924
• КОНСПЕКТ (по презентации)
Солдатова Гульнара Тагировна
gulnara.soldatova@yandex.ru
2. Содержание
• РАЗДЕЛ 1. Основания математики (задача 1)• РАЗДЕЛ 2. Элементы линейной алгебры и
аналитической геометрии (задачи 2 и 3)
• РАЗДЕЛ 3. Элементы математического
анализа (задачи 4-7)
3. § 1. Элементы теории графов
Раздел 1. Основанияматематики
§ 1. Элементы теории
графов
4.
Определение.Граф - это упорядоченная пара G = G(V, E), где
V - непустое множество вершин,
E – множество ребер
Множество вершин: V = { v1 , v2 , …, vn }
Множество ребер (дуг): E = { e1 , e2 , ….., em }
5.
Примеры графов:6.
ОТНОШЕНИЯРЕБРАМИ
МЕЖДУ
ВЕРШИНАМИ
И
1) Две вершины графа называются смежными,
если существует соединяющее их ребро.
2) Два ребра называются смежными, если они
имеют общую вершину.
3) Если вершина v является концом ребра е, то
говорят, что вершина v инцидентна ребру е.
7. Определение.
• Число рёбер, инцидентных вершине v,называется степенью этой вершины и
обозначается (v)
• Если степень вершины равна нулю, то
вершину называют изолированной.
8.
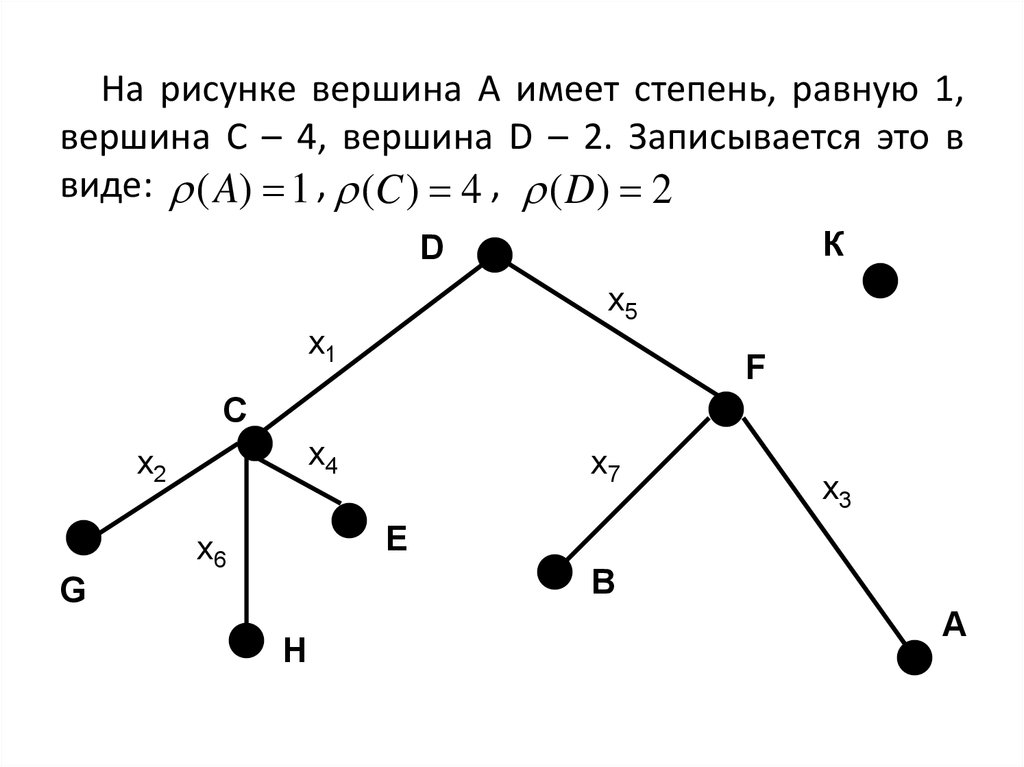
На рисунке вершина А имеет степень, равную 1,вершина С – 4, вершина D – 2. Записывается это в
виде: ( A) 1 , (C ) 4 , ( D ) 2
К
D
х5
х1
F
С
х4
х2
х7
х3
E
х6
B
G
H
A
9. Способы задания графа
1) Матрица инцидентности - таблица, состоящая из nстрок (вершины) и т столбцов (рёбра), в которой:
bij 1 , если вершина vi инцидентна ребру e j ;
bij 0 , если вершина v не инцидентна ребру e j .
i
! Петля учитывается дважды!
10.
2) Матрица смежности графа G (V , E )- квадратная таблица А порядка n, в которой:
aij равно количеству ребер, соединяющих
вершину vi с вершиной v j .
! Петля учитывается дважды!
11.
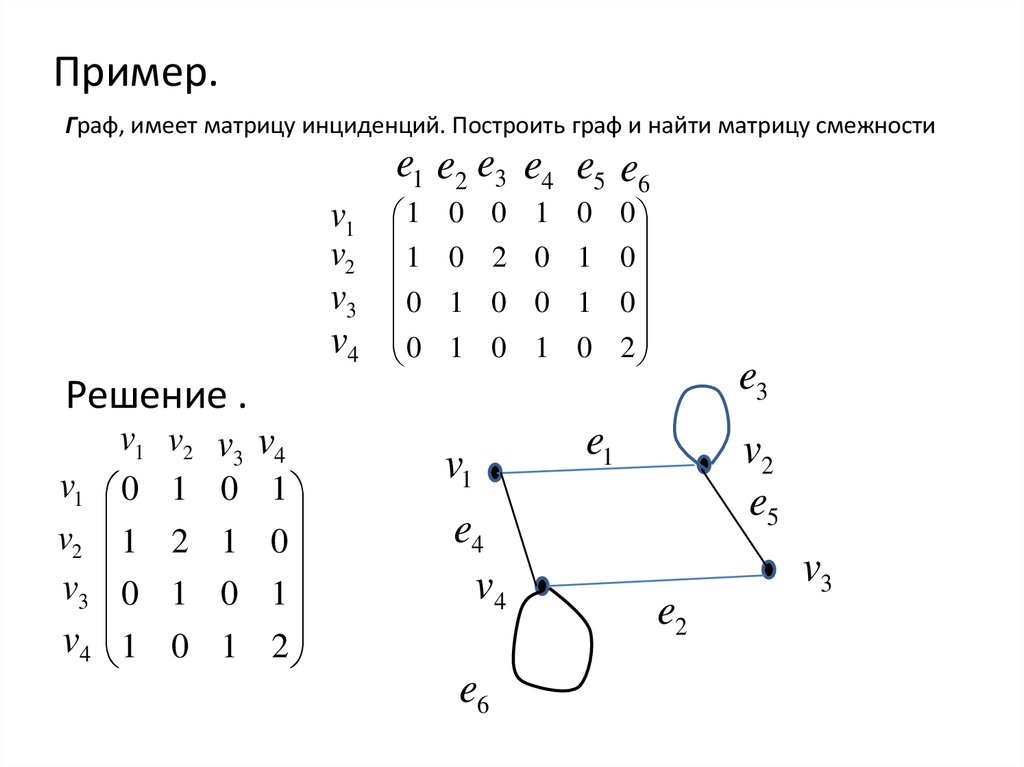
Пример.Граф, имеет матрицу инциденций. Построить граф и найти матрицу смежности
e1 e2 e3 e4 e5 e6
v1 1 0 0 1 0 0
v2
v3
v4
1 0 2 0 1 0
0 1 0 0 1 0
0 1 0 1 0 2
e3
Решение .
v1 v2 v3 v4
v1 0 1 0 1
v2 1 2 1 0
v3 0 1 0 1
v4 1 0 1 2
v1
e4
v4
e6
e1
v2
e5
e2
v3
12. Раздел 2. Элементы линейной алгебры и аналитической геометрии
§ 1. Матрицы. Операции над ними.§ 2. Определители.
§3. Обратная матрица
§ 4. Решение СЛАУ.
§ 5. Векторная алгебра.
§ 6. Аналитическая геометрия.
13.
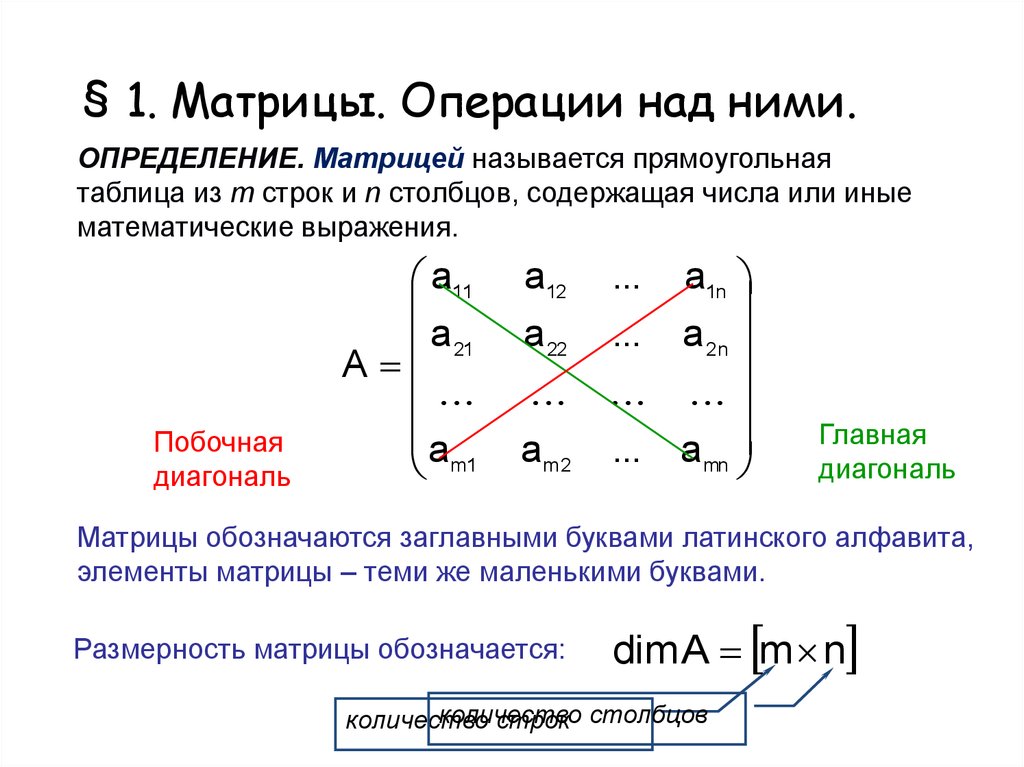
§ 1. Матрицы. Операции над ними.ОПРЕДЕЛЕНИЕ. Матрицей называется прямоугольная
таблица из m строк и n столбцов, содержащая числа или иные
математические выражения.
Побочная
диагональ
a11
a 21
A
a
m1
a12
a 22
am 2
a1n
... a 2n
... amn
...
Главная
диагональ
Матрицы обозначаются заглавными буквами латинского алфавита,
элементы матрицы – теми же маленькими буквами.
Размерность матрицы обозначается:
dim A m n
количество
количество
строк столбцов
14. ВИДЫ МАТРИЦ
1) Если m n , то матрица называется прямоугольной.2) Если m n , то матрица называется квадратной (n - ного
порядка).
1 6 0
A
2 4 5
1 0
B
4 5
3) Матрица типа 1 n называется вектор-строкой:
a
11
a12 a13 ... a1n
Матрица типа m 1 называется вектор-столбцом:
a11
a 21
...
a
m1
15.
4) Квадратная матрица называется единичной, если ееэлементы,
расположенные
на
главной
диагонали,
равны
единице, остальные – нулю (обозначается буквой Е):
1 0 0
E 0 1 0
0 0 1
5) Если все элементы квадратной матрицы равны нулю, то она
называется нулевой матрицей и обозначается символом 0.
0 0 0
O 0 0 0
0 0 0
16.
6) Квадратная матрица называется диагональной, еслиэлементы, стоящие вне главной диагонали равны нулю
2 0 0
A 0 3 0
0 0 1
7) Квадратная матрица называется треугольной, если элементы,
стоящие ниже (выше) главной диагонали равны нулю:
4
0 0
2 5
2
B 0 3 7 C 9 3 0
0 0
2 5 1
1
17. Действия над матрицами
Равенство матрицМатрицы равны, если они имеют одинаковую размерность и их
соответствующие элементы равны.
Транспонирование матрицы
Операция получения из данной матрицы транспонированной
заменой каждой строки столбцом с тем же номером
1 3 2
A
0 1 4
Сложение (вычитание) матриц
1 0
T
A 3 1
2 4
Сумма и разность матриц существуют только для матриц
одинакового размера, при этом соответствующие элементы
матриц складываются или вычитаются.
18.
Умножение матрицы на числоПри умножении матрицы A на число k получается матрица того же
размера, при этом каждый элемент матрицы A умножается на k.
Найти значение выражения:
1 3 2
A
0 1 4
C A 5 B
2 4 1
B
5 0 2
Решение:
10 20 5
5 B
0 10
25
11 17 7
A 5B
25 1 14
19.
Умножение матрицПроизведение матриц A
*
B определено только тогда, когда
число столбцов матрицы А равно числу строк матрицы В, в
противном случае произведение не существует.
Произведением матрицы A размера [m n]
с элементами aij
на матрицу B размера[n k ] с элементами bjq называется
матрица C размера [m k ] с элементами:
n
c iq aij b jq
j 1
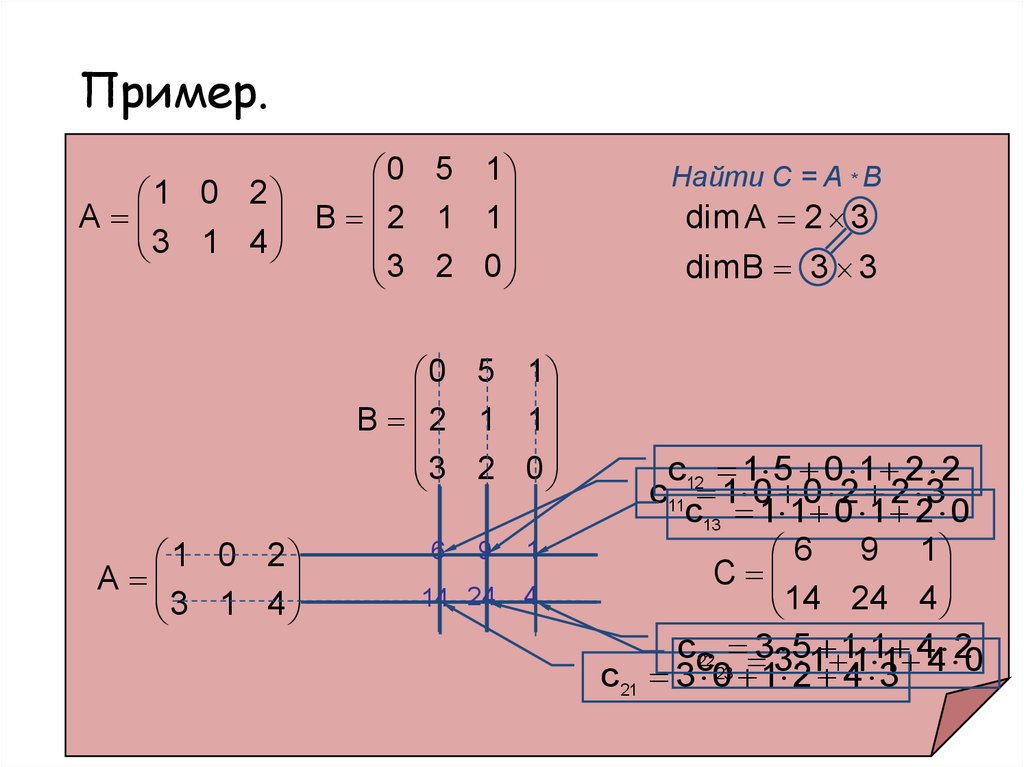
20. Пример.
1 0 2A
3 1 4
0 5 1
B 2 1 1
3 2 0
Найти С = A * B
dim A 2 3
dimB 3 3
0 5 1
B 2 1 1
3 2 0
1 0 2
A
3 1 4
9
1
14 24
4
6
c12 1 5 0 1 2 2
c11 1 0 0 2 2 3
c13 1 1 0 1 2 0
6 9 1
C
14 24 4
cc22 33 5 1 11 1
44 20
1
c 21 3 023 1 2 4 3
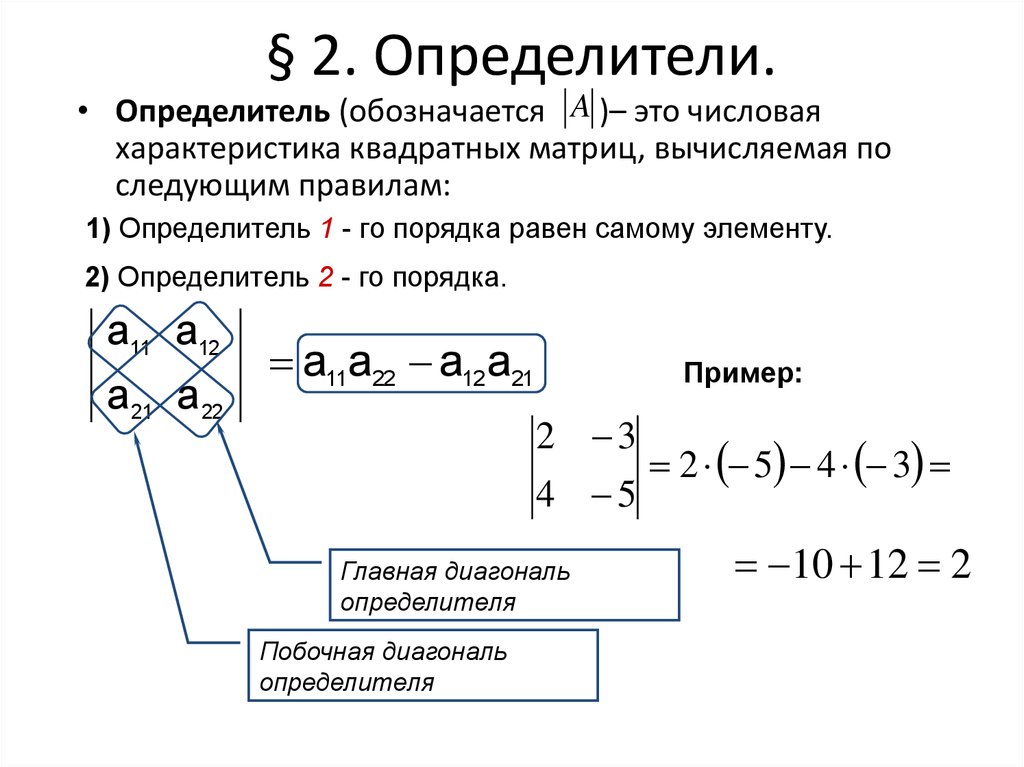
21. § 2. Определители.
• Определитель (обозначается A )– это числоваяхарактеристика квадратных матриц, вычисляемая по
следующим правилам:
1) Определитель 1 - го порядка равен самому элементу.
2) Определитель 2 - го порядка.
a11 a12
a21 a22
a11a22 a12 a21
Пример:
2 3
4 5
Главная диагональ
определителя
Побочная диагональ
определителя
2 5 4 3
10 12 2
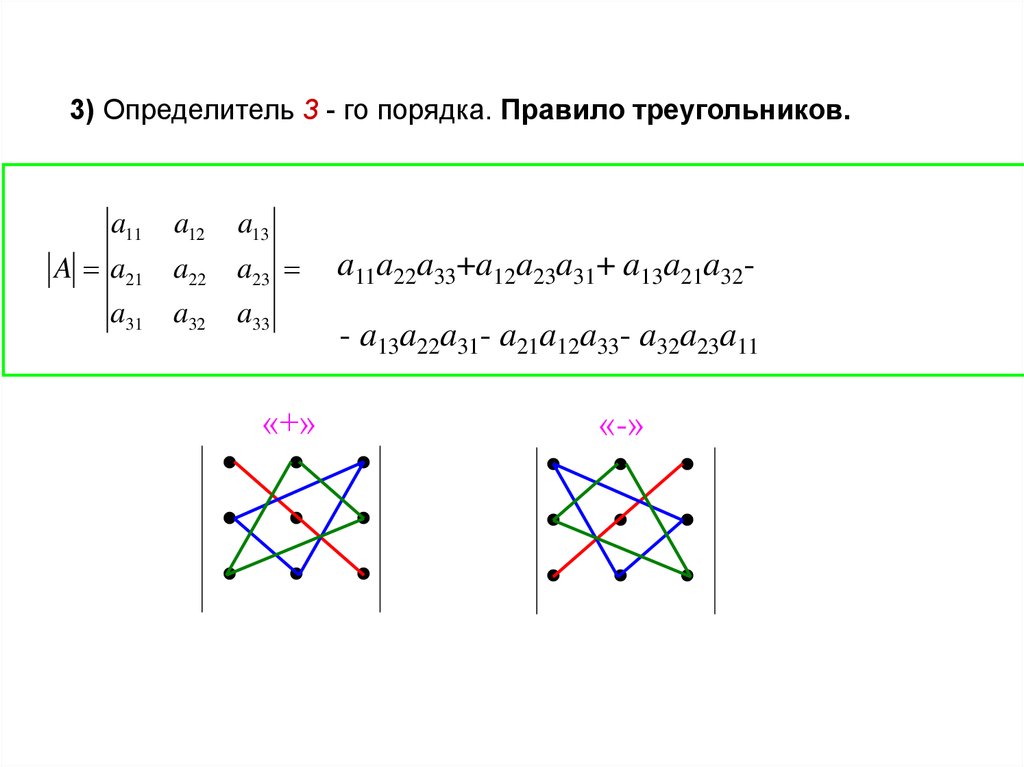
22.
3) Определитель 3 - го порядка. Правило треугольников.a11
a12
a13
A a21
a22
a23
a31
a32
a33
«+»
a11a22a33+a12a23a31+ a13a21a32-
- a13a22a31- a21a12a33- a32a23a11
«-»
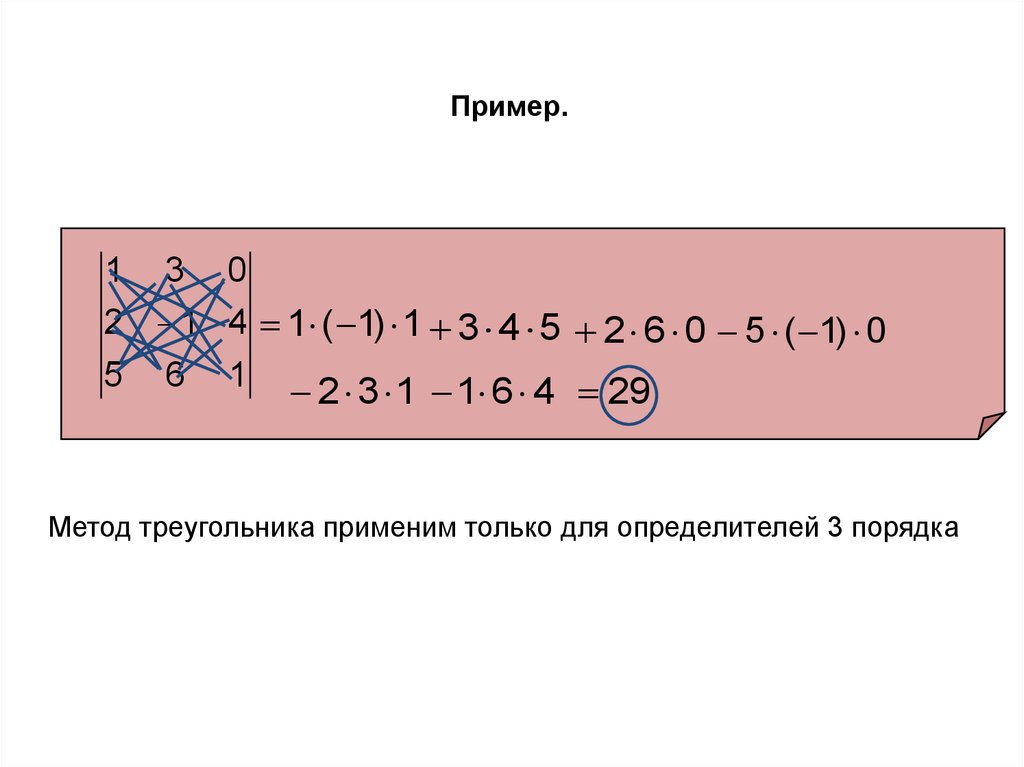
23. Пример.
13
0
2 1 4 1 ( 1) 1 3 4 5 2 6 0 5 ( 1) 0
5 6 1 2 3 1 1 6 4 29
Метод треугольника применим только для определителей 3 порядка
24. 3) Определитель n - го порядка.
• Правило Лапласа (разложение по элементам строки(столбца)
Определитель n-го порядка равен сумме произведений элементов
некоторой строки (столбца) на их алгебраические дополнения
n
A ai1 Ai1 ai 2 Ai 2 ... ain Ain ai j Ai j
j 1
Алгебраическим дополнением элемента
Ai j ( 1) i j M i j
ai j
называется
Mi j - минор элемента ai j - это oпределитель, который получается
из определителя n - го порядка путем вычеркивания i - й строки и j - го
столбца, т.е. строки и столбца, на пересечении которых стоит
элемент
ai j
25. Пример.
2 1 00 3 1
2 5 1
2 A11 1 A12 0 A13
2 1
1 1
3 1
5 1
1 1
1 2
0 1
2 1
0 1
2 (3 1 5 1) 1 (0 1 2 1) 2
1 3
0 3
2 5
26.
Свойства определителя n-го порядка:1. Определитель матрицы А равен определителю
транспонированной матрицы, т.е. А АТ .
2. Если все элементы некоторой строки матрицы А равны 0, то
определитель равен 0.
3. Общий множитель всех элементов строки определителя можно
вынести за знак этого определителя.
4. Если в определителе поменять местами две строки, то он изменит
знак на противоположный.
5. Если определитель имеет две равные строки, то он равен 0.
27.
Если6.
элементы
двух
строк
определителя
пропорциональны, то определитель равен 0.
7. Значение определителя не изменится, если к элементам
его
некоторой
строки
прибавить
соответствующие
элементы другой строки, умноженные на одно и то же
число k.
28. §3. Обратная матрица
Определение. Квадратная матрица А-1 называется обратнойматрицей по отношению к квадратной матрице A n - ного
порядка, если выполняется условие:
АА-1=А-1А=Е,
где A, А-1, Е – одного порядка.
Теорема. Обратная матрица существует и единственна тогда и
только тогда, когда A 0 .
A11 A21 A31
1
1
A
A12 A22 A32
det A
A
A
A
13 23 33
29. §4. Метод обратной матрицы решения систем линейных уравнений
Метод обратной матрицы рассмотрим на примеререшения квадратной системы 3 порядка.
a11 x1 a12 x 2 a13 x 3 b1
a 21 x1 a 22 x 2 a 23 x 3 b 2
a x a x a x b
32 2
33 3
3
31 1
Запишем эту систему в матричном виде. Обозначим:
a11 a12
A a 21 a 22
a
31 a 32
a13
a 23
a 33
x1
X x2
x3
b1
B b2
b3
Основная матрица
Матрица - столбецМатрица - столбец
системы свободных членов
неизвестных
30.
Тогда систему можно записать так:A X B
Найдем решение системы в матричном виде.
Предположим, что det A отличен от нуля и, следовательно,
существует обратная матрица А-1.
Умножим слева матричную запись системы на обратную матрицу:
A 1 A X A 1 B
E X A 1 B
X A 1 B
Метод обратной матрицы применим для решения квадратных
систем с невырожденной основной матрицей.
31. Метод обратной матрицы решения систем линейных уравнений
Решить систему методом обратной матрицы.3 x 2 x 3 1
2x1 4 x 2 x 3 2
2x 2x 3
2
1
X A 1 B
1 0 .5
1
1
A 1 1
1
2
3
3
0 3 1
A 2 4 1
2 2 0
x1
X x2
x3
1
B 2
3
1
B 2
3
-0,5
2
-5
0 .5
X 2
5
32. §5. Метод Крамера.
Рассмотрим систему из трех уравнений с тремя неизвестными:a11 x1 a12 x 2 a13 x 3 b1
a 21 x1 a 22 x 2 a 23 x 3 b 2
a x a x a x b
32 2
33 3
3
31 1
a11 a12 a13
a 21 a 22 a 23
a 31 a 32 a 33
Δ- главный определитель системы. Рассмотрим вспомогательные
определители, которые получаются из главного определителя,
заменой соответствующего столбца столбцом свободных членов:
b1 a12 a13
a11 b1 a13
a11 a12 b1
1 b 2 a 22 a 23
2 a21 b2 a23
3 a 21 a 22 b 2
b 3 a 32 a 33
a31 b3 a33
a 31 a 32 b 3
33. Теорема (правило Крамера).
Пусть - определитель матрицы системы А,j -определитель, полученный из заменой j - го столбца
столбцом свободных членов В.
Тогда, если 0 , система линейных уравнение имеет
единственное решение, определяемое по формулам Крамера:
3
1
2
x1 ; x2
; x3
Или в общем случае, для системы из n уравнений с n
неизвестными:
1
x1 ;
2
x2
;
n
xn
34.
4 x1 2 x2 x3 0,x 2 x x 1,
2
3
1
x2 x3 3,
Пример: Решить систему уравнений
по формулам Крамера.
4 2 1
A 1 2
1 11 0,
0 1 1
значит система имеет единственное решение, определяемое
формулами Крамера
1
2
3
x1 , x2 , x3 .
0
1 1
2 1
2
4
0
1
1 11, 2 1
1
1 11,
3 1 1
0 3 1
1 11
x1
1,
11
2 11
x2
1,
11
4 2
3 1 2
0
1 22,
0 1 3
3 22
x3
2.
11
35.
Рассмотрим систему линейных уравненийa11 x1 a12 x 2 a13 x 3 b1
a 21 x1 a 22 x 2 a 23 x 3 b 2
a x a x a x b
32 2
33 3
3
31 1
где числа а11, а12,…а33 – коэффициенты системы,
b1, b2,b3 - свободные члены системы,
х1, х2,х3 - неизвестные.
a11 a12 a13 b1
A a21 a22 a23 b2
a a a b
31 32 33 3
Расширенная матрица
системы
36. Метод Гаусса решения систем линейных уравнений
Суть метода: с помощью элементарных преобразований надстроками расширенная матрица приводится к треугольному виду.
Следующие действия над расширенной матрицей системы
называются элементарными преобразованиями.
Умножение или деление элементов строк на одно и то же
число, не равное нулю
Перестановка местами двух строк
Прибавление к элементам строки элементов другой строки,
умноженных на произвольный множитель.
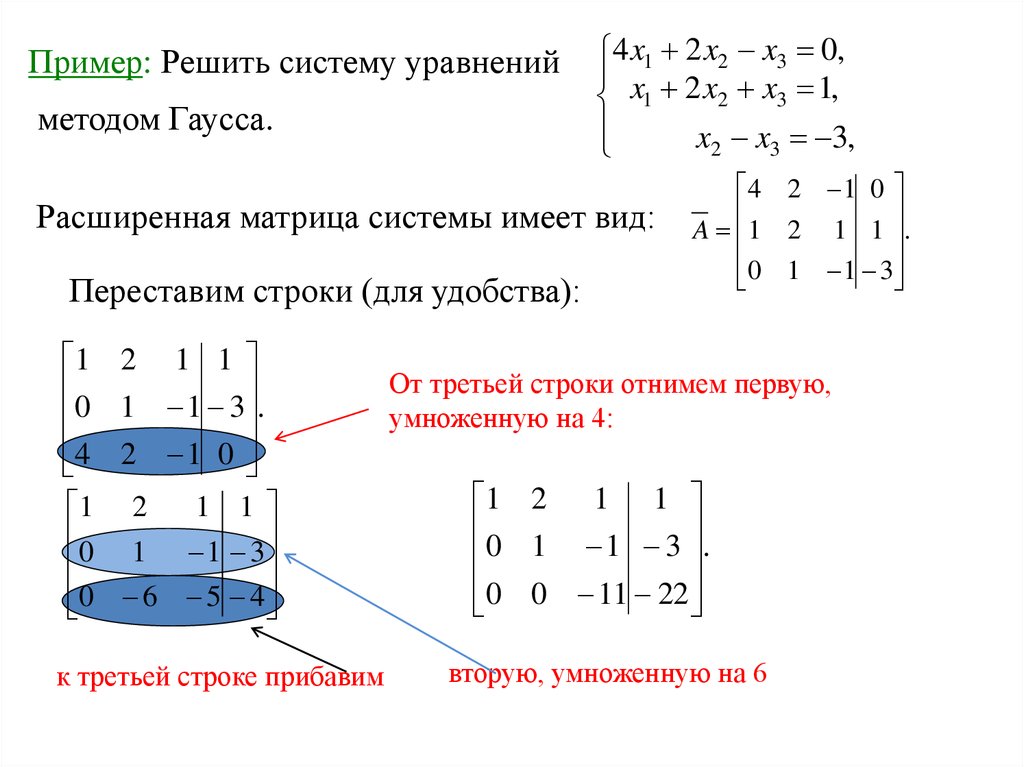
37.
Пример: Решить систему уравненийметодом Гаусса.
4 x1 2 x2 x3 0,
x 2 x x 1,
2
3
1
x2 x3 3,
Расширенная матрица системы имеет вид:
Переставим строки (для удобства):
1 2 1 1
0
1
1
3
.
4 2 1 0
1 2
1 1
0
1
1
3
0 6 5 4
к третьей строке прибавим
4 2 1 0
A 1 2 1 1 .
0 1 1 3
От третьей строки отнимем первую,
умноженную на 4:
1 2 1 1
0
1
1
3
.
0 0 11 22
вторую, умноженную на 6
38.
1 2 1 10
1
1
3
.
0 0 11 22
третью строку разделим
на (-11)
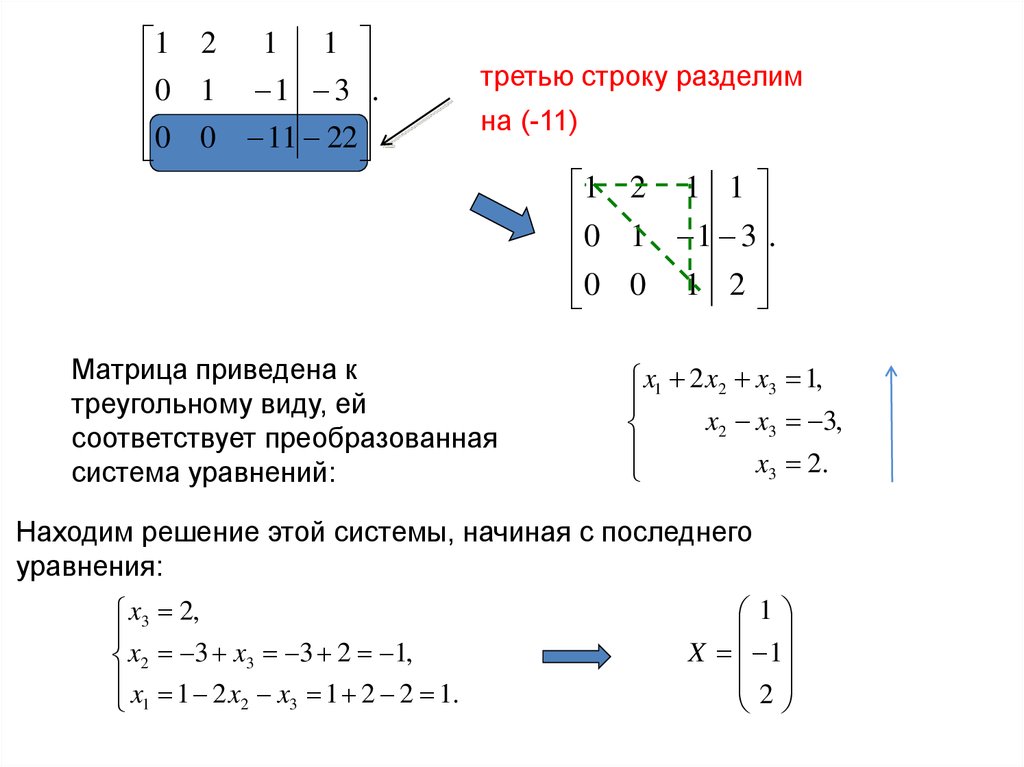
Матрица приведена к
треугольному виду, ей
соответствует преобразованная
система уравнений:
1 2 1 1
0
1
1
3
.
0 0 1 2
x1 2 x2 x3 1,
x2 x3 3,
x3 2.
Находим решение этой системы, начиная с последнего
уравнения:
x3 2,
x2 3 x3 3 2 1,
x 1 2 x x 1 2 2 1.
2
3
1
1
X 1
2





























 Математика
Математика








