Аппроксимирующий полином Ньютона

1.

Аппроксимирующий полином
Ньютона

2.

Задача. Придать интерполяционной формуле более
простой вид. Слагаемые должны располагаться в
порядке убывания их значимости.

3.

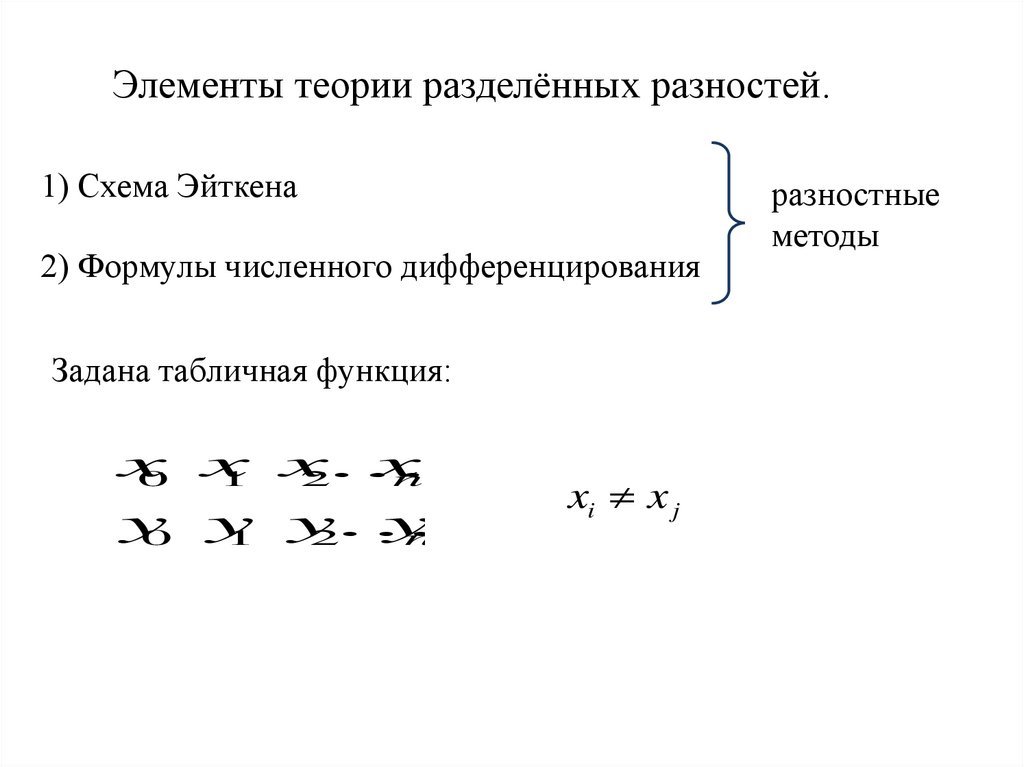
Элементы теории разделённых разностей.
1) Схема Эйткена
2) Формулы численного дифференцирования
Задана табличная функция:
x
x
0 x
1 x
2
n
y
y
y
y
0
1
2
n
xi x j
разностные
методы

4.

f1 f0
,
f x
,x
0
1
x
x
1
0
f2 f1
,
f x
,x
1
2
x
x
2
1
fn
fn
1
f
x
,x
n
1
n
x
x
n
n
1
разделённые разности первого порядка
f
x
,
x
f
x
,
x
1
2
0
1
f
x
,
x
,
x
,
0
1
2
x
x
2
0
f
x
,
x
f
x
,
x
n
1
n
n
2
n
1
f
x
,
x
,
x
n
2
n
1
n
x
x
n
n
2
разделённые
разности второго
порядка

5.

f
x
,
,
x
f
x
,
,
x
i
1
i
k
i
i
k
1
f
x
,
x
,
,
x
i
i
1
i
k
x
x
i
k
i
разделённая разность k-го порядка
Полезные свойства разделённых разностей
1) Разделённая разность k-го порядка равна:
f
x
i
l
f
x
,
x
,
,
x
i
i
1
i
k
x
x
l
0
i
l
j
k
i
j

6.

2) Разделённая разность суммы или разности функций равна
сумме или разности разделённых разностей слагаемых,
соответственно уменьшаемого и вычитаемого.
3) Постоянный множитель
разделённой разности.
можно
выносить
за
знак
4) Разделённая разность есть симметрическая функция своих
аргументов, т.е.
f
x
,
x
,
,
x
f
x
,
x
,
x
,
,
x
i
i
1
i
k
i
1
i
i
2
i
k
5) Разделённая разность многочлена понижает на единицу его
степень.
x
x
n
2n
1
f x x : f
x
,
x
x
x
x
x
x
x
i
1
i
i
x
x
n
nn
1n
2
i
1
i n
ii
1
i
1i
1
i
i
1
i

7.

Вывод:
Разделённые разности n-го порядка многочлена n-й
степени Pn x постоянны. (Все последующие равны
нулю)
Свойство
5
применяют
для
определения
предпочтительной степени многочлена, подходящего
для
интерполирования
данной
функции.
Или
используют для обнаружения ошибок в таблицах
многочленов или функций, близких к ним.

8.

Построим таблицу разделённых разностей
i
xi
yi
0
0
0
1
2
8
2
3
27
3
5
4
5
f xi , xi 1
8 0
4
2 0
27 8
19
3 2
f x
i,x
i
1,x
i
2
19 4
5
3 0
f xi , xi 3
10 5
1
5 0
10
1
49
14
1
125
91
12
6
216
43
1
1
f x x3

9.

Строим полином Ньютона
Задана табличная функция:
x
x
x
0
1 x
2
n
f0
f1 f2
fn
При построении полинома Ньютона в качестве базисных
функций возьмем следующие:
1
,
x
x
,
x
x
x
x
,
,
x
x
x
x
x
x
0
0
1
0
1
n
1
Многочлен ищем в виде:
N
x
a
a
x
x
a
x
x
x
x
n
0
1
0
2
0
1
a
x
x
x
x
x
x
n
0
1
n
1

10.

График многочлена должен проходить через заданные узлы, т.е.
N
x
fi, i
1
,n
i
Из этих условий найдём коэффициенты:
x0 a0 f0
N
N
x
f
a
x
x
f
1
0
1
1
0
1
h
N
x
f
a
x
x
a
x
x
x
x
f
2
0
1
2
0
2
2
0
2
1
2
2
h
2
h
h

11.

a0 f0 − разделённая разность 0-го порядка
f1 f0 − разделённая разность 1-го порядка
a1
x1 x0
f1 f0
x
f2 f0
x
2
0
x
x
f
f
a
x
x
1
0
2
0
1
2
0
a
2
x
x
x
x
x
x
x
x
2
0
2
1
2
0
2
1
f
x
x
f
x
x
f
x
x
f
x
x
2
1
0
0
1
0
1
2
0
0
2
0
x
x
x
x
x
x
2
0
2
1
1
0
f
f
f
2
1
0
x
x
x
x
x
x
x
x
x
x
x
x
2
0
2
1
1
2
1
0
0
2
0
1
− разделённая разность 2-го порядка

12.

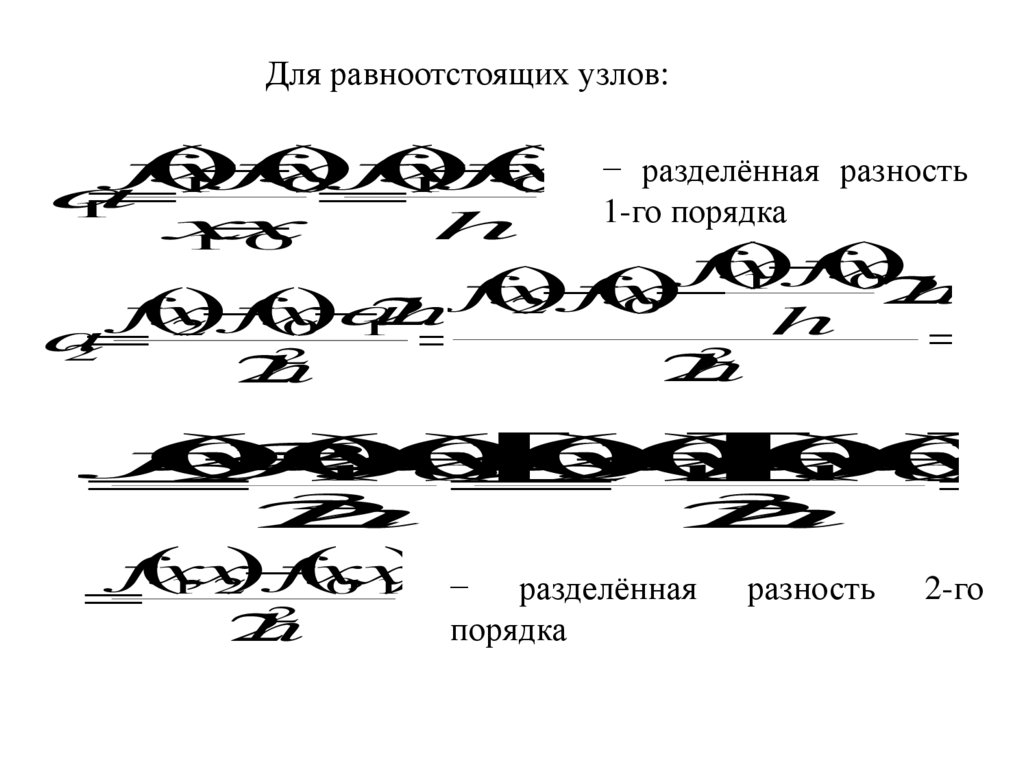
Для равноотстоящих узлов:
− разделённая разность
f
x
f
x
f
x
f
x
1
0
1
0
a
1
1-го порядка
x
x
h
1 0
f
x
f
x
1
0
f
x
f
x
2
h
2
0
f
x
f
x
a
2
h
h
2
0
1
a
2
2
2
2
h
2
h
f
x
2
f
x
f
x
f
x
f
x
f
x
f
x
2
1
0
2
1
1
0
2
2
2
h
2
h
f
x
,x
f
x
,x
1
2
0
1
− разделённая разность 2-го
2
порядка
2
h

13.

Общая формула для коэффициента многочлена Ньютона
имеет вид:
f
x
,
x
,
,
x
0
1
k
a
;k
0
,
n
k
k
k
!
h
Окончательный вид многочлена Ньютона:
N
x
f
x
f
x
,
x
x
x
f
x
,
x
,
x
x
x
x
x
n
0
0
1
0
0
1
2
0
1
f
x
,
x
,
,
x
x
x
x
x
x
x
0
1
n
0
1
n
1
Первый
интерполяционный
интерполирования вперёд.
многочлен
Ньютона
для
Этой формулой пользуются для вычисления значений функции
в узлах левой(верхней) части таблицы.

14.

4) Разделённая разность есть симметрическая функция своих
аргументов, т.е.
f
x
,
x
,
x
f
x
,
x
,
x
f
x
,
x
,
x
0
1
2
1
0
2
2
1
0
Если 0 ↔ n, 1 ↔ n − 1, 2 ↔ n − 2 и т.д., тогда
N
x
a
a
x
x
a
x
x
x
x
n
0
1
n
2
n
n
1
a
x
x
x
x
x
x
n
n
n
1
1
N
x
f
x
f
x
,
x
x
x
f
x
,
x
,
x
x
x
x
x
n
n
n
n
1
n
n
n
1
n
2
n
n
1
f
x
,
x
,
,
x
x
x
x
x
x
x
n
n
1
0
n
n
1
1
Второй
интерполяционный
интерполирования назад.
многочлен
Ньютона
для

15.

Погрешность многочлена Ньютона.
f
x
N
x
f
x
,
x
,
,
x
x
n
0
n
n
где
при
n
f
f
x
,x
,
,x
0
n
n
!
x xk 0
n
1
f
x
f
x
,
x
,
,
x
f
x
,
,
x
0
n
0
n
1
n
1
!

16.

Пример. Вычислить в точках x = 0,1 и x = 4,5 значения
функции, заданной таблично.
i
xi
yi
f xi , xi 1
0
0
1
1
2
1
2
3
1
5
2
3
2
3
5
5
3
2
f xi , xi 3
f x
i,x
i
1,x
i
2
3
6
3
10

17.

При x 0.1
воспользуемся первой формулой Ньютона.
2
f
0
.
1
N
0
.
1
1
1
0
.
1
0
0
.
1
0
0
.
1
2
3
3
0
.
1
0
0
.
1
2
0
.
1
3
10
2
1
19
3
1
19
29
1
.
1
3
10
10
10
10
10
10
1
.
1
0
.
127
0
.
166
1
.
393
При x 4.5
воспользуемся второй формулой Ньютона.
3
5
f
4
.
5
N
4
.
5
5
4
.
5
5
4
.
5
5
4
.
5
3
2 6
3
3.854
4
.
5
5
4
.
5
3
4
.
5
2
10

18.

Возможна такая нумерация узлов:
x
y
y
2 y
y 2
y 2
x 1
y 1
y 1
2 y 1
x0
y0
y0
2 y0
x1
y1
y1
2 y1
x2
y2
y2
n y0
x 2
n y
Многочлен Гаусса