Релятивистская механика. Релятивистский импульс. Взаимосвязь массы и энергии в СТО. (Лекция 7)

1. Лекция 7

1

2.

Контрольный вопрос
Команда космического корабля смотрит 2-часовой
фильм на борту корабля.
Для наблюдателя на Земле, смотрящего тот же фильм
с помощью телескопа через иллюминатор корабля,
продолжительность фильма:
а) > 2 часов, б) < 2 часов, в) = 2 часам.
t t p
Часы в движущейся системе отсчета
кликают реже, чем в неподвижной.
а)
2

3.

Содержание предыдущей лекции
Кинематика и динамика вращательного движения
• Гироскопические силы. Гироскопы и их применение в технике.
Релятивистская механика
• Постулаты специальной теории относительности (СТО)
Эйнштейна
• Относительность одновременности и преобразования Лоренца.
• Парадоксы релятивистской кинематики: сокращение длины и
замедление времени в движущихся системах отсчета.
• Преобразования скоростей в релятивистской кинематике.
3

4.

Содержание сегодняшней лекции
Релятивистская механика
Релятивистский импульс.
Взаимосвязь массы и энергии в СТО.
Сохранение релятивистского импульса.
Релятивистская энергия.
Механические колебания
• Гармонические колебания: амплитуда, частота и фаза колебаний.
• Кинематическая и векторная форма представления колебаний.
• Идеальный гармонический осциллятор. Уравнение идеального
осциллятора и его решение.
• Свободные затухающие колебания.
• Вынужденные колебания. Время установления вынужденных
колебаний и его связь с добротностью.
4

5.

Релятивистский импульс
Требования к релятивистскому выражению:
• выполнение законов физики,
• получение выражения классической физики
при малых скоростях.
5

6.

Релятивистский импульс
Релятивистское выражение для импульса:
mu
p
mu ,
u2
1 2
c
u - cкорость частицы, m – масса частицы.
u << c
1
1,
p mu.
u2
1 2
c
6

7.

Релятивистское выражение для силы
dp
F
,
dt
где p
mu
mu.
u2
1 2
c
7

8.

p
mu
u2
1 2
c
mu
Релятивистское выражение
для кинетической энергии
x2
x2
dp
Работа внешних сил над частицей W Fdx
dx
dt
x1
x1
du / dt u 2u / c 2 (du / dt )
dp d mu
m
3
/
2
2
dt dt
u2
u2
1 u
1 2
2 1 2
2
c
c
c
u2 u2
m du / dt 1 2 2
c
c m(du / dt )
3
/
2
2
2 3/ 2
u
u
1 2
1 2
c
c
8

9.

x2
dp m(du / dt )
dt u 2 3 / 2
1 2
c
x2
dp
W Fdx dx
dt
x1
x1
Релятивистское выражение для кинетической энергии
t
W
0
m(du / dt )udt
u2
1 2
c
W
3/ 2
u
m
0
mc 2
u
u2
1 2
c
3/ 2
du
mc 2
u2
1 2
c
9

10.

Релятивистское выражение для кинетической энергии
Равенство работы внешних сил над частицей
приобретенной ею кинетической энергии
W K.
K
mc 2
mc 2 mc 2 mc 2 ( 1)mc 2
u2
1 2
c
Подтверждение справедливости данного выражения
в экспериментах на ускорителях частиц.
Малые скорости:
1
K mu 2
2
10

11.

K
mc 2
mc 2 mc 2 mc 2 ( 1)mc 2
u2
1 2
c
Релятивистское выражение для полной энергии
E0 mc - энергия покоя
2
Полная энергия частицы E K mc
E
mc 2
2
mc 2
u2
1 2
c
Масса - форма энергии.
11

12.

Соотношение между энергий и импульсом
E
mc 2
mc 2
p mu
u2
1 2
c
E 2 p 2c 2 (mc2 ) 2
12

13.

Механические колебания
13

14.

Механические колебания
Колебания –
движения или процессы, обладающие той
или иной повторяемостью во времени.
14

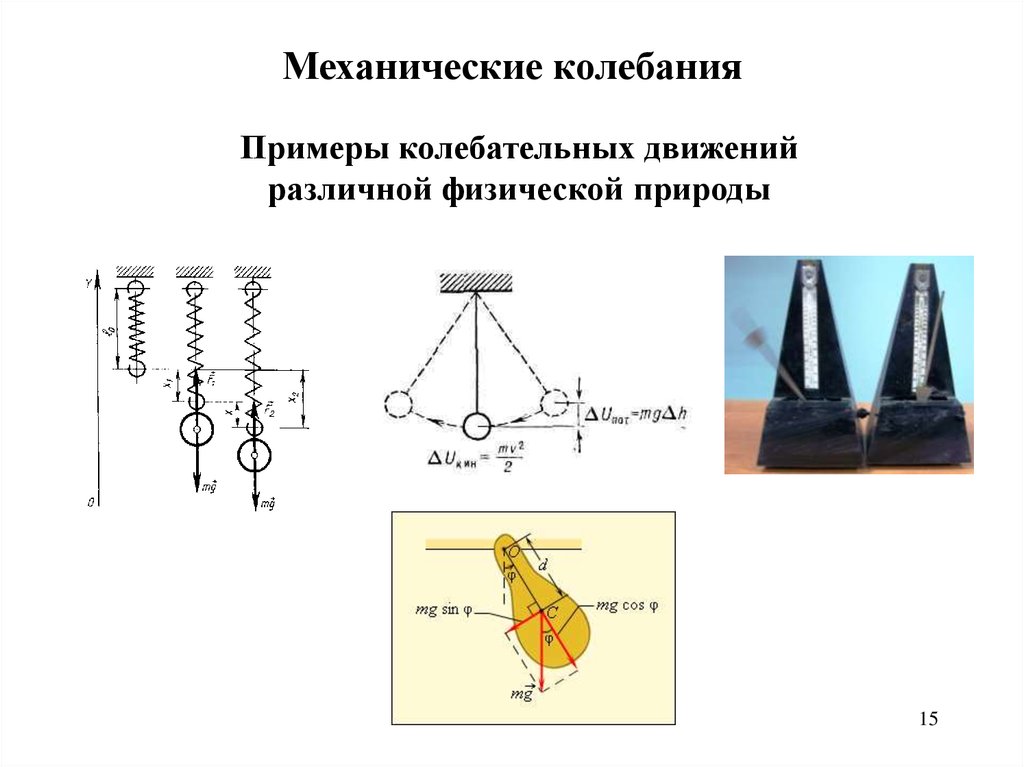
15.

Механические колебания
Примеры колебательных движений
различной физической природы
15

16.

Механические колебания
Примеры колебательных движений
различной физической природы
16

17.

Механические колебания
Примеры колебательных движений
различной физической природы
17

18.

Механические колебания
Примеры колебательных движений
различной физической природы
18

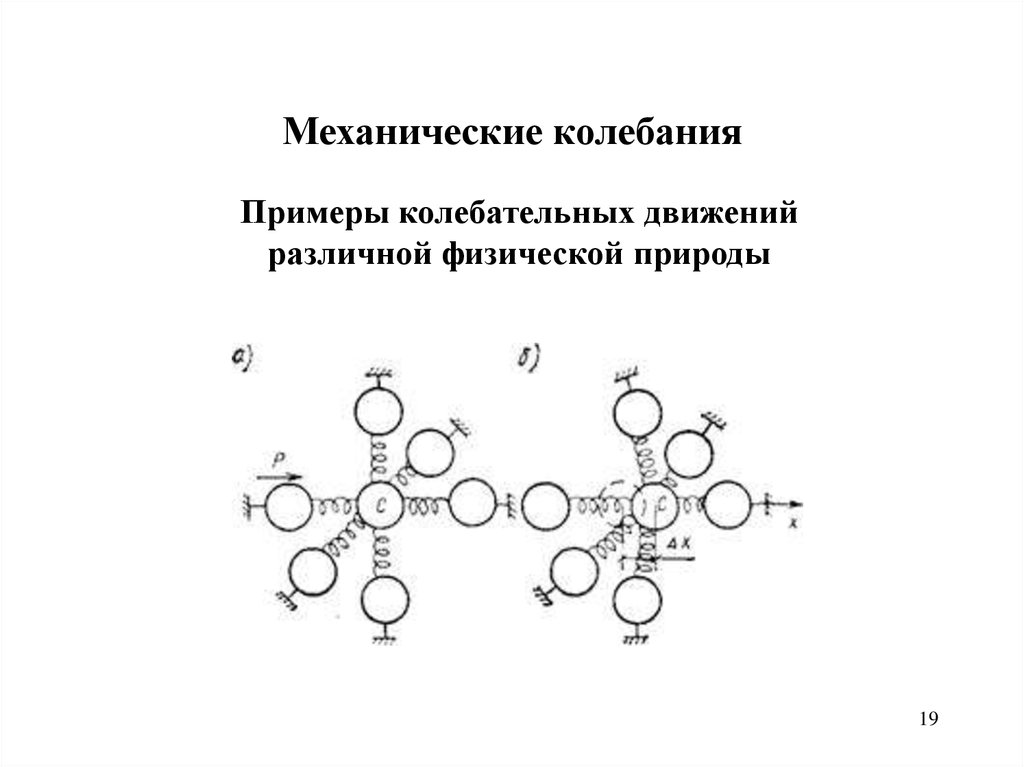
19.

Механические колебания
Примеры колебательных движений
различной физической природы
19

20.

Механические колебания
Примеры колебательных движений
различной физической природы
20

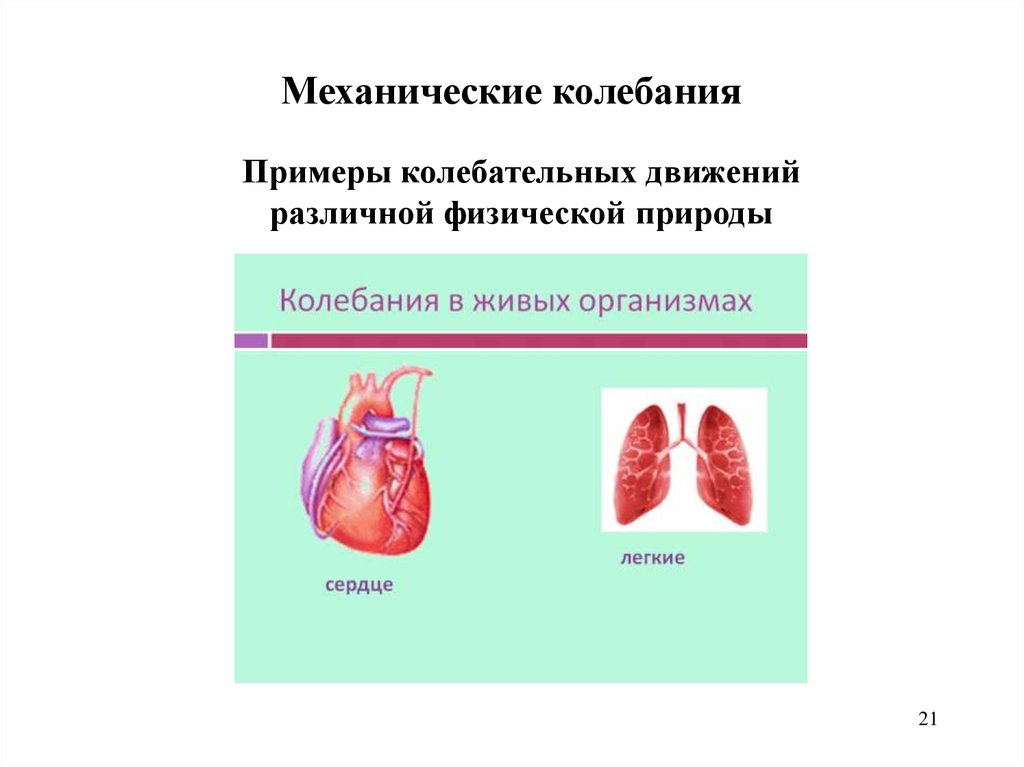
21.

Механические колебания
Примеры колебательных движений
различной физической природы
21

22.

Механические колебания
Гармонические колебания –
колебания, при которых колеблющаяся величина
изменяется со временем по закону синуса или косинуса.
Гармонические колебания –
частое наблюдение в природе и технике.
Периодические процессы иной формы
(с другой зависимостью от времени) –
результат наложения нескольких гармонических колебаний.
22

23.

Гармонические колебания
Закон Гука:
возвращающая сила
Fs = - kx.
- kx = max
k
ax x
m
23

24.

k
ax x
m
Кинематическая форма представления
гармонических колебаний
2
d x
k
x
2
dt
m
k
m
2
d 2x
2
x
2
dt
Решение: x(t ) A cos t
Проверка:
dx
d
A cos t A sin t
dt
dt
d 2x
d
2
A
sin
t
A cos t
2
dt
dt
24

25.

x(t ) A cos t
Кинематическая форма представления
гармонических колебаний
А, , - параметры колебательного движения.
А – амплитуда или максимальное отклонение от
положения равновесия,
k
- циклическая или круговая частота,
m
- начальная фаза,
t - фаза колебательного движения.
25

26.

x(t ) A cos t
Кинематическая форма представления
гармонических колебаний
=0
0
26

27.

x(t ) A cos t
Кинематическая форма представления
гармонических колебаний
(t T ) ( t ) 2
Период Т – время, необходимое для совершения телом
полного цикла колебательного движения.
T
2
Частота колебаний – число колебаний в единицу времени
1
f
T 2
27

28.

x(t ) A cos t
Кинематическая форма представления
гармонических колебаний
2
2 f
T
2
m
T
2
k
1
k
f 2
T
m
28

29.

Смещение колеблющегося тела
x(t ) A cos t
xmax A
Скорость колеблющегося тела
dx
v
A sin t
dt
k
vmax A
A
m
Ускорение колеблющегося тела
d 2x
a 2 2 A cos t
dt
d 2x
k
2
amax 2 A A
dt
m 29

30.

Векторная форма представления
гармонических колебаний
Связь между равномерным круговым движением точки Р и
гармоническими колебаниями точки Q.
x(t ) A cos t
Равномерное круговое движение – комбинация двух
гармонических колебаний вдоль оси x и вдоль оси y.
30

31.

Затухающие колебания
Реальные ситуации: действие, помимо линейной
возвращающей силы, неконсервативных сил (таких как
сила трения), затрудняющих колебательный процесс.
Частый случай:
сила сопротивления среды
R bv ,
b – коэффициент сопротивления среды,
v скорость.
31

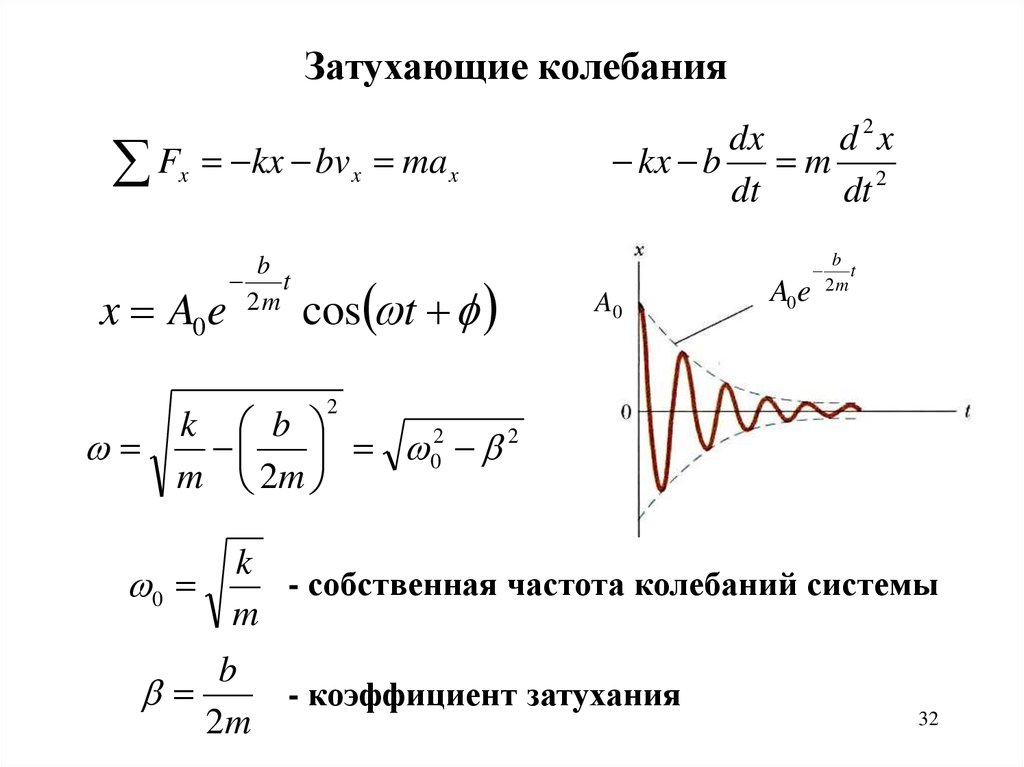
32.

Затухающие колебания
F
x
kx bv x ma x
x A0 e
b
t
2m
cos t
dx
d 2x
kx b m 2
dt
dt
A0
A0 e
b
t
2m
2
k b
2
2
0
m 2m
k
- собственная частота колебаний системы
0
m
b
- коэффициент затухания
2m
32

33.

2
0
b
2m
2
R bv
Затухающие колебания
периодические колебания
R max < bvmax b/2m < 0
33

34.

x A0 e
t
cos t
Затухающие колебания
Характеристика колебательной системы декремент затухания
A(t )
e T .
A(t T )
Характеристика колебательной системы логарифмический декремент затухания
A(t )
ln
T .
A(t T )
34

35.

x A0 e t cos t
A(t )
ln
T
A(t T )
Затухающие колебания
A A0 e t A0 e
t
T
.
t= :
Ne = / T - число полных колебаний за время .
Предположение: уменьшение амплитуды в e раз.
exp (- /T ) = exp (-1).
/T = Ne = 1,
= 1 / Ne.
Логарифмический декремент затухания –
величина, обратная числу колебаний,
совершаемых за время уменьшения амплитуды в е раз.
35

36.

= 1 / Ne
Затухающие колебания
Характеристика колебательной системы - добротность
Q = / = Ne.
Пропорциональность добротности Q числу колебаний Ne,
совершаемых системой за то время ,
за которое амплитуда колебаний уменьшается в е раз.
36

37.

Вынужденные колебания
Возможность компенсации потерь энергии колебаний
при затухающих колебаниях за счет внешней силы,
совершающей положительную работу над системой.
F (t ) F0 sin t
37

38.

Вынужденные колебания
F ma
dx
d 2x
F0 sin t b kx m 2
dt
dt
x A cos t
A
F0 / m
2
2 2
0
b
m
2
38

39.

A
F0 / m
2
2 2
0
b
m
2
Вынужденные
колебания
Резонанс – резкое возрастание амплитуды колебаний
вблизи собственной частоты колебаний системы.
Причина резонанса –
вынуждающая сила в фазе со скоростью колебаний системы.
Мощность, сообщаемая осциллятору при резонансе,
максимальна.
39

40.

Вынужденные колебания
Резонансные кривые при различных уровнях затухания
Q1 (колебательная
система без трения)
Q2
Q3 < Q2
Q4 < Q3 < Q2
x0
Низкие
частоты
(ω << ω0)
А= xm ≈ x0.
Высокие
частоты
(ω >> ω0)
А= xm → 0.
Cмещение резонансной кривой в сторону низких частот
при не очень высоких Q (< 10) .
40

41.

Контрольный вопрос
Груз массы m, прикрепленный к пружине,
отведен в положение x = А и отпущен.
За полный цикл колебаний груз преодолеет путь, равный:
а) А/2,
б) А,
в) 2А,
г) 4А.
41