Похожие презентации:
Предел последовательности
1.
Пределпоследовательности
Лекция 4
2.
СодержаниеПоследовательности
Предел
последовательности
Свойства предела
последовательности
3.
Точка a (конечная или бесконечноудаленная) числовой прямой называется
пределом
некоторой
числовой
последовательности
действительных
чисел, если, какова бы ни была
окрестность точки а, она содержит все
члены
рассматриваемой
последовательности
начиная
с
некоторого номера.
de f
⟺
a=lim x n ❑
n→∞
∃ n ϵ ∀ n> nϵ : x n ∈ U ( a , ϵ )
4.
Если числовая последовательностьимеет конечный предел, то она
называется сходящейся
∃ a∈ R ∀ ϵ >0 ∃ nϵ ∈ N ∀ n> nϵ :∨ x n− a∨¿ ϵ
de f
⟺
a=lim x n ❑
n→∞
∀ ϵ >0 ∃ nϵ ∈ N ∀ n>n ϵ : a−ϵ < x n < a+ ϵ
5.
Последовательность, пределом которойявляется бесконечность, называется
бесконечно большой
def
⟺
lim x n =∞ ❑
n→∞
1
∀ ϵ > 0 ∃n ϵ ∈ N ∀ n> nϵ :∨x n∨¿
ϵ
de f
⟺
lim x n =+∞ ❑
n→∞
de f
⟺
lim x n =−∞ ❑
n→∞
1
∀ ϵ > 0 ∃n ϵ ∈ N ∀ n>n ϵ : x n >
ϵ
−1
∀ ϵ > 0 ∃n ϵ ∈ N ∀ n>n ϵ : x n <
ϵ
lim x n =+∞ или lim x n =− ∞ ⟹ lim x n = ∞
n→∞
n→∞
n→∞
6.
Примеры1
∀ ϵ > 0∃ n ϵ ∈ N : nϵ > ⟹
ϵ
1
1
∀ n ∈ N n> nϵ : 0< n < n <ϵ ⟹
ϵ
lim 1
n→∞
=0
n
∀ a ∈ R ∃ ϵ >0 (FE: 0< ϵ < 1) ∀ n ∈ N :
π
x 2 n=sin 2 n=0 ⟹
π
⟹ lim sin n≠ a
2
n→∞
7.
Примерыn→∞
∃ ϵ >0 FE : ϵ=1
∀ n0 ∈ N ∃ n∈ N n>n0 :
1
n> ⟹
ϵ
⟹ lim n=∞
n →∞
1
π
sin n → 0
n
2
∀ ϵ >0 ∃ n0 ∈ N ∀ n ∈ N n>n 0 :
1
π
1
¿ n s in 2 n∨≤ n <ϵ ⟹
lim 1
π
n→∞
⟹ n sin 2 n=0
8.
Конечная или бесконечно удаленная точкаа числовой прямой не является пределом
последовательности, если найдется такая
окрестность точки а, за пределами
которой лежит бесконечное число членов
последовательности.
lim x n ≠ a ⟺ ∃ ϵ >0 ∀ n 0 ∈ N ∃ n> n0 : x n ∉ U ( a , ϵ )
n→∞
9.
Доказатьlim x n =a ⟹ lim ¿ x n∨¿∨ a∨¿
n→∞
n→∞
¿
10.
Точка а расширенной числовой прямой называется пределомпоследовательности точек этой прямой, если, какова бы ни
была окрестность точки а, она содержит все члены
рассматриваемой последовательности начиная с некоторого
номера
1
∀ n ∈ N x n ∈U (a , ), то lim x n =a
Если последовательность такова, что
n
n→∞
∀ U (a , ϵ ), ϵ>0 ∃n ∈ N :
1
U (a , n )⊂U (a , ϵ).
1
Для этого достаточно взять такое n: <ϵ
n
1
∀ U (a)∃ n0 ∈ N :U (a , )⊂U (a)⟹
n0
∀ n>n0 :
1
1
U (a , n )⊂U (a , n )⊂U (a)⟹
0
lim x n=a
n→ ∞
11.
Пример неограниченной, неявляющейся бесконечно большой
12.
Последовательность точек расширеннойчисловой прямой может иметь на этой
прямой только один предел
«от противного»
lim x n=a , lim x n=b .
n→∞
n →∞
Выберем непересекающиеся окрестности ϵ 1 >0, ϵ 2 >0 :
U (a , ϵ 1 )∩U (b , ϵ 2)=⊘.
lim x n =a ⟹ ∃ n1 ∀ n>n1 : x n ∈ U (a , ϵ 1)
n→∞
lim x n=b ⟹ ∃n 2 ∀ n>n2 : x n ∈ U (a , ϵ 2)
n →∞
Числовая
n0 =m a x {n1 , n 2 }:
последовательнос
∀ n> n0 : x n ∈ U (a , ϵ 1 )∧ x n ∈U (b , ϵ 2)⟹
ть может иметь
x n ∈U (a , ϵ 1)∩U (b , ϵ 2)∧
только один
U (a , ϵ 1 )∩U (b , ϵ 2 )=⊘
предел, конечный
N o ns en se
или
определенного
знака
13.
Свойства пределовпоследовательностей
∀ n ∈ N x n =a ⟹ lim x n =a
n→∞
x n ∈ R , y n ∈ R , z n ∈ R , x n ≤ y n ≤ z n ∧ lim x n= lim z n=a ∈ R ⟹ lim y n=a
n →∞
n →∞
n→∞
Доказательство:
Выберем произвольно окрестность точки а: U (a).
lim x n =a ⟺ ∃n1 : ∀ n>n 1 x n ∈U (a)
n→∞
lim z n =a ⟺∃ n2 : ∀ n>n 2 z n ∈U (a)
n→∞
n0 =m a x {n1 , n 2 }: x n ∈ U (a)∧ z n ∈ U (a)∀ n>n 0 ⟹
y n ∈U (a)∀ n>n 0 ⟹
lim y n=a
n→∞
14.
x n ∈ R , y n ∈ R , a∈ R , b ∈ R ,lim x n=a , lim y n =b ,
n→∞
n →∞
a <b ⟹ ∃ n0 ∀ n>n 0 x n < y n .
Доказательство:
Пусть U (a)∩V (b)=⊘.
∀ x ∈ U ∧ y ∈V , x < y .
∃n 0 ∀ n> n0 x n ∈U , y n ∈V ⟹
∃ n0 ∀ n>n 0 x n< y n .
15.
Если числоваяпоследовательность имеет
конечный предел, то она
Последовательностьограничена.
ограничена,
если
ограничено
множество значений последовательности.
Доказательство:
Пусть lim x n=a ,ϵ=1.
n→ ∞
∃n 0 ∀ n>n0 ∨x n−a∨¿1.
d=m a x {1,∨ x 1−a∨,∨x 2 −a∨,…,∨x n −a∨}⟹
¿ x n −a∨¿ d ,
a−d <x n <a+d.
0
16.
Верхняя (нижняя) грань множества значенийэлементов последовательности является верхней
(нижней) гранью данной последовательности.
Последовательность
называется
возрастающей
(убывающей) последовательностью, если для каждый
следующий элемент больше (меньше) предыдущего.
17.
ТЕОРЕМА ВЕЙЕРШТРАССАВсякая возрастающая числовая последовательность имеет
предел, конечный, если она ограничена сверху, и бесконечный,
если она не ограничена сверху, причем
{
lim x n = x n }
n→∞
Доказательство:
{
Пусть β = x n }.
Выберем произвольную окрестность U (β ),
′
β - левый конец U (β ). ⟹
Следствие:
Для
того
чтобы
возрастающая
последовательность
сходилась, необходимо и
достаточно, чтобы она
была ограничена сверху.
1 ∀ n ∈ N x ≤ β ; ¿ 2 ∃ n : ∀ x > β ′ . ¿ x > x ⟹ ¿ β ′ < x ≤ x β ⟹ ¿ ∀ n > : x ∈ U ( β ) ⟹ ¿ l im x = β . ¿
n 0 n n+ 1 n n n 0 n n
¿
n→∞
0
0
18.
ТЕОРЕМАБОЛЬЦАНО-ВЕЙЕРШТРАССА
Из
любой
ограниченной
последовательности
можно
выделить сходящуюся подпоследовательность, а из любой
неограниченной последовательности - бесконечно большую
подпоследователельность,
имеющую
своим
пределом
бесконечность определенного знака.
Доказательство:
1. \{ x n }- ограничена . ⟹
∃[a , b ]: a ≤ x n ≤ b ∀ n ∈ N .
Разделим отрезок на два равных. x n ∈[a 1 , b 1].
Продолжим: x n ∈[a 2 , b 2 ], n2 >n1 …
1
2
′′
′
x n ∈ [ ak , b k ] , nk > nk , k >k .
k
′ ′
′
19.
ТЕОРЕМАБОЛЬЦАНО-ВЕЙЕРШТРАССА
Из
любой
ограниченной
последовательности
можно
выделить сходящуюся подпоследовательность, а из любой
неограниченной последовательности - бесконечно большую
подпоследователельность,
имеющую
своим
пределом
бесконечность определенного знака.
{ x n }−подпоследовательность x n .
b−a
Система вложенных отрезков [ ak , b k ], bk −a k = k → 0, k → ∞ .
2
k
∃ α=∩[a k ,b k ].
lim ak =lim b k =α .
n→∞
n→∞
ak ≤ x n ≤ bk ⟹
lim {x n }=α .
k
n→∞
k
20.
Предел, конечный или определенного знакабесконечный, подпоследовательности данной
последовательности называется ее частичным
пределом.
Всякая последовательность имеет хотя бы
один частичный конечный или бесконечный
предел, причем заведомо конечный, если
данная последовательность ограничена.
Вопрос:
Доказать, что точка расширенной числовой
прямой
является
пределом
последовательности тогда и только тогда,
когда в любой ее окрестности содержится
бесконечно
много
членов
данной
последовательности.
21.
Критерий Коши сходимости последовательностиДля того чтобы последовательность сходилась,
необходимо и достаточно, чтобы она была
фундаментальной.
Фундаментальная ∀ ϵ >0 ∃ n ∈ N ∀ n ∈ N ∀ m ∈ N ,
ϵ
последовательнос n >n , m>n :∨x −x ∨¿ ϵ .
ϵ
ϵ
n
m
ть
ϵ
ϵ
1lim x =a⟹¿∀ϵ>0∃n ∈N∀n∈N,n>n ,:¿∨x −a∨¿ϵ.¿n>n ,m>n :¿∨x −x ∨¿∨(x −a)+(a−x )∨≤∨x −a∨+¿x −a∨¿ + <ϵ.¿
n
ϵ ϵ n ϵ ϵ n m n m n m 22
¿ n→ ∞
22.
Критерий Коши сходимости последовательностиДля того чтобы последовательность сходилась,
необходимо и достаточно, чтобы она была
фундаментальной.
ϵ
ϵ
ϵ
2∨x− ¿ϵ:=1⟹∃n>,mn:¿∨x− ¿1.n>,m=+1:∨x− ¿1⟹x−1< x+1∀n>⟹¿ограниче.⟹∃{x}:lim =a⟹¿∀ϵ>0∃k∈N∀ ,k>¿n :∨x−a¿.∃n>,mn:∨x− ¿.n=max{,n}¿∨x−a x+−a∨≤x ∨+¿x−a +<ϵ.¿
n m 1 1 n m 1 1 n + 1 n +1 n +1 1 n n ϵ ϵ k n 2 ϵ ϵ n m 2 0 ϵ k n n n n n 2
¿ n→∞
1 1 1 kk
ϵk
ϵ kk k k




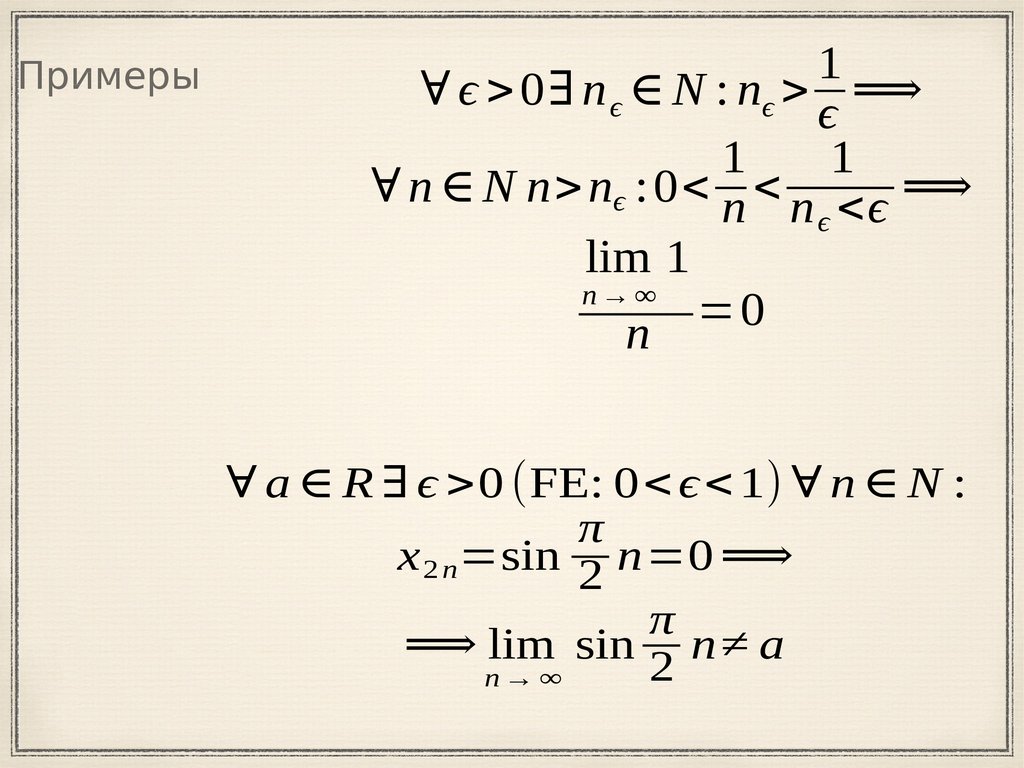















 Математика
Математика








