Похожие презентации:
Поверхности. Лекция №4
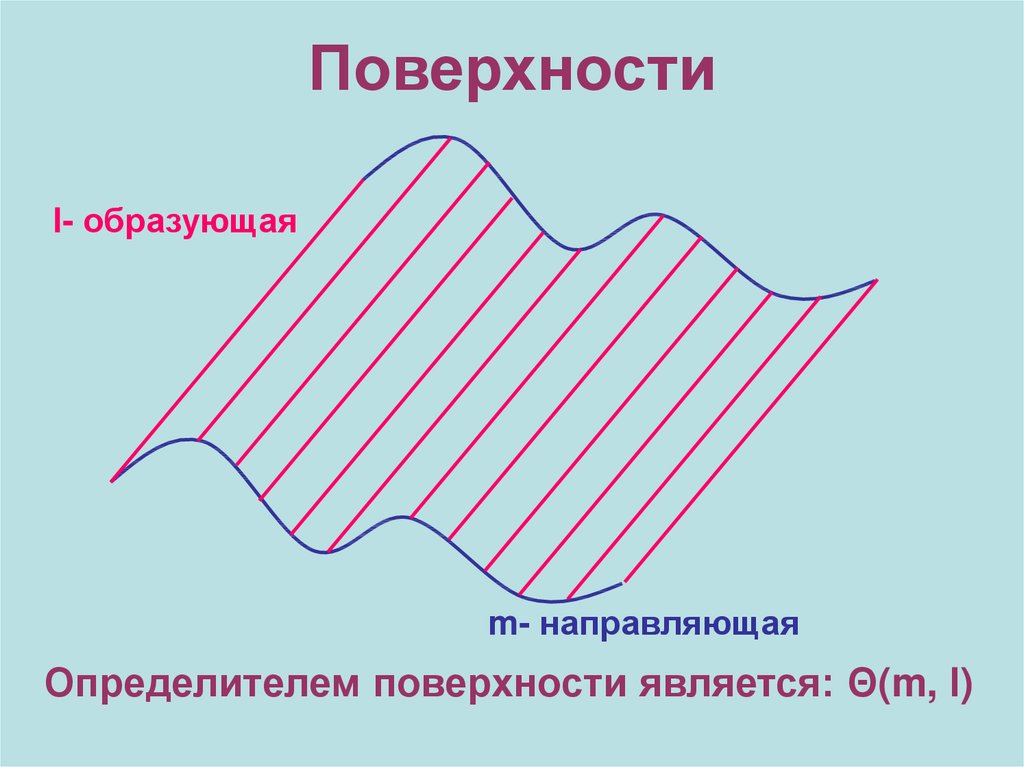
1. Поверхности
l- образующаяm- направляющая
Определителем поверхности является: Θ(m, l)
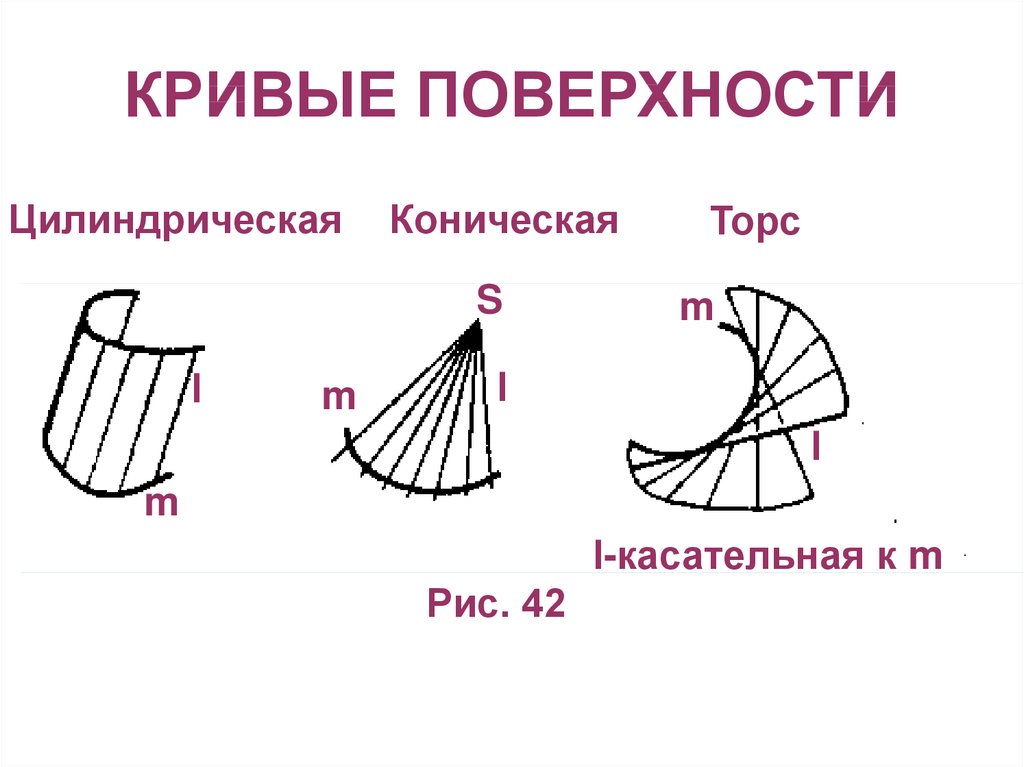
2. КРИВЫЕ ПОВЕРХНОСТИ
ЦилиндрическаяКоническая
S
l
m
Торс
m
l
l
m
l-касательная к m
Рис. 42
3. КРИВЫЕ ПОВЕРХНОСТИ
Косаяплоскость
l
m
Цилиндроид
Коноид
l
n
n
m
m
l
l
l- параллельна направляющей плоскости Σ
и пересекает m и n.
Рис. 43
n
4. КРИВЫЕ ПОВЕРХНОСТИ
Эллипсоидi
Тор
i
Однополостный
гиперболоид
i
Рис. 44
Двуполостный
гиперболоид
i
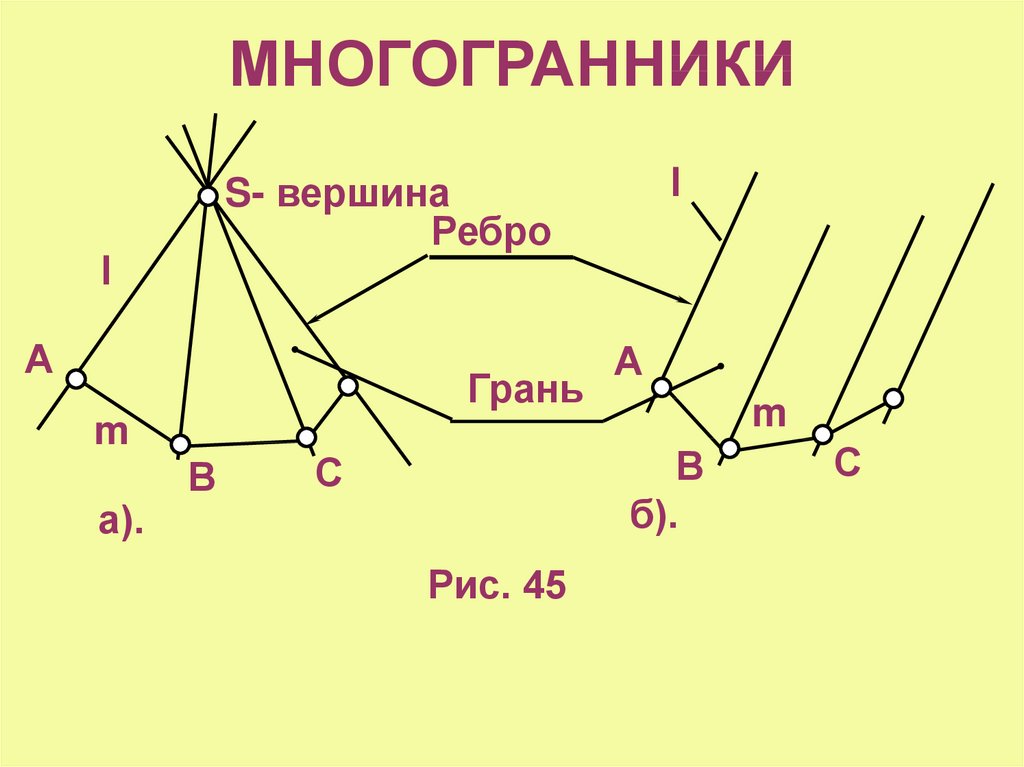
5. МНОГОГРАННИКИ
lS- вершина
Ребро
l
А
Грань
m
а).
В
А
m
В
б).
С
Рис. 45
С
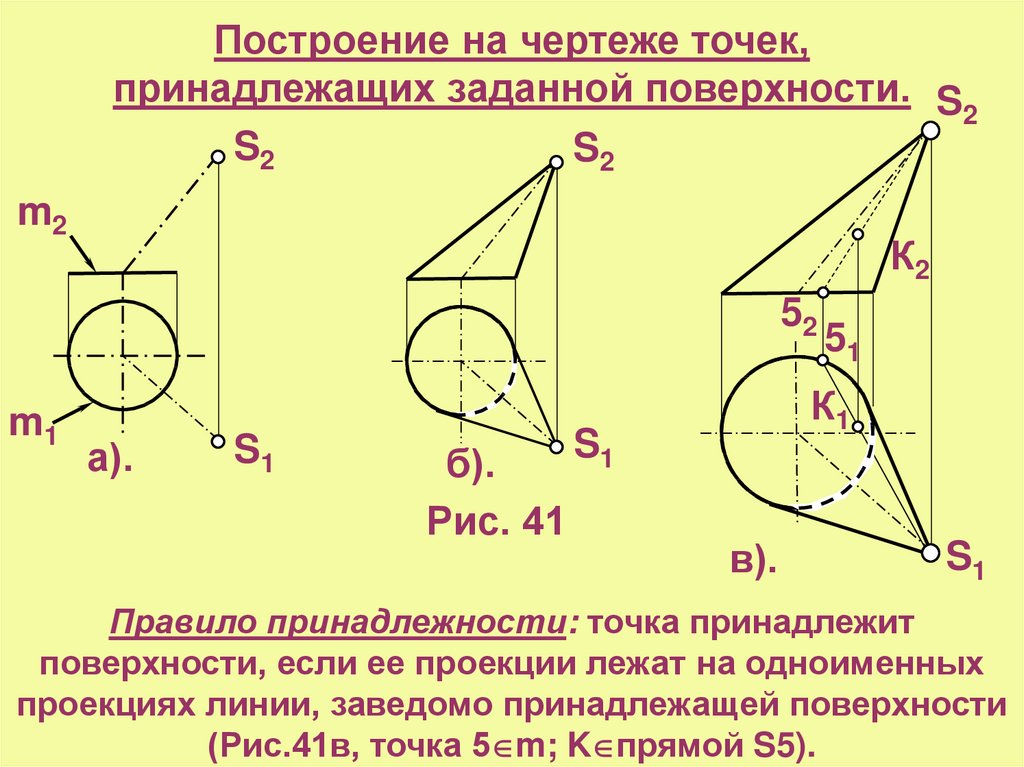
6. Построение на чертеже точек, принадлежащих заданной поверхности.
S2
S2
S2
m2
К2
52
m1
а).
S1
S1
б).
Рис. 41
51
К1
в).
S1
Правило принадлежности: точка принадлежит
поверхности, если ее проекции лежат на одноименных
проекциях линии, заведомо принадлежащей поверхности
(Рис.41в, точка 5 m; K прямой S5).
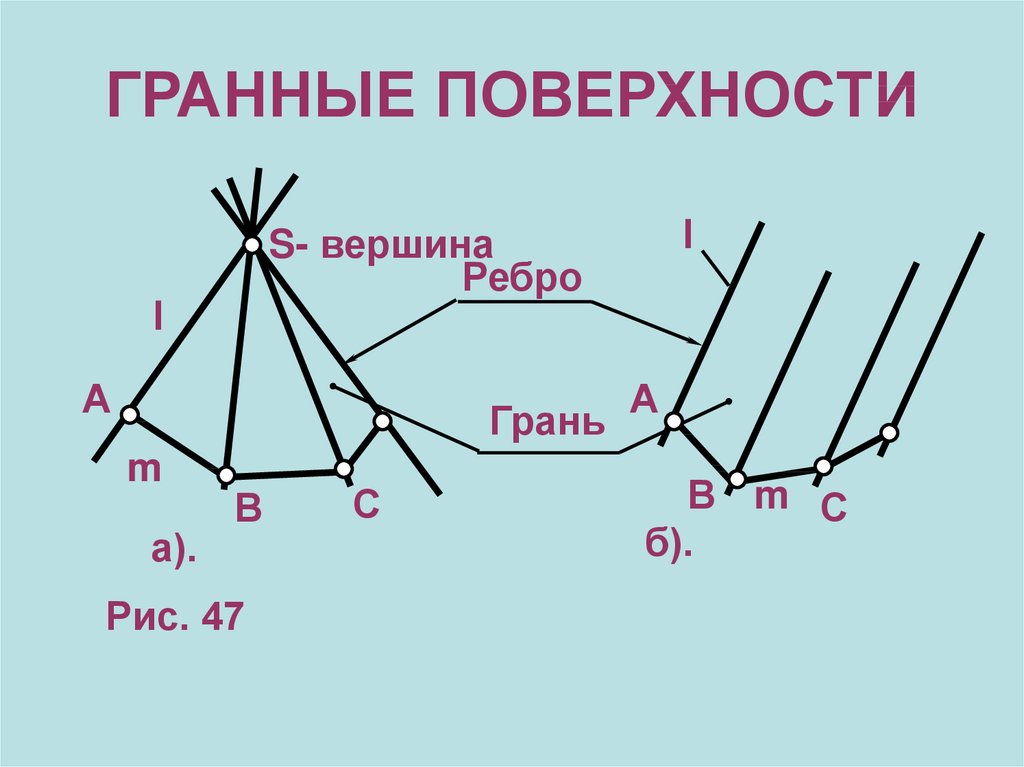
7. ГРАННЫЕ ПОВЕРХНОСТИ
lS- вершина
Ребро
l
А
Грань
m
а).
В
Рис. 47
С
А
В m С
б).
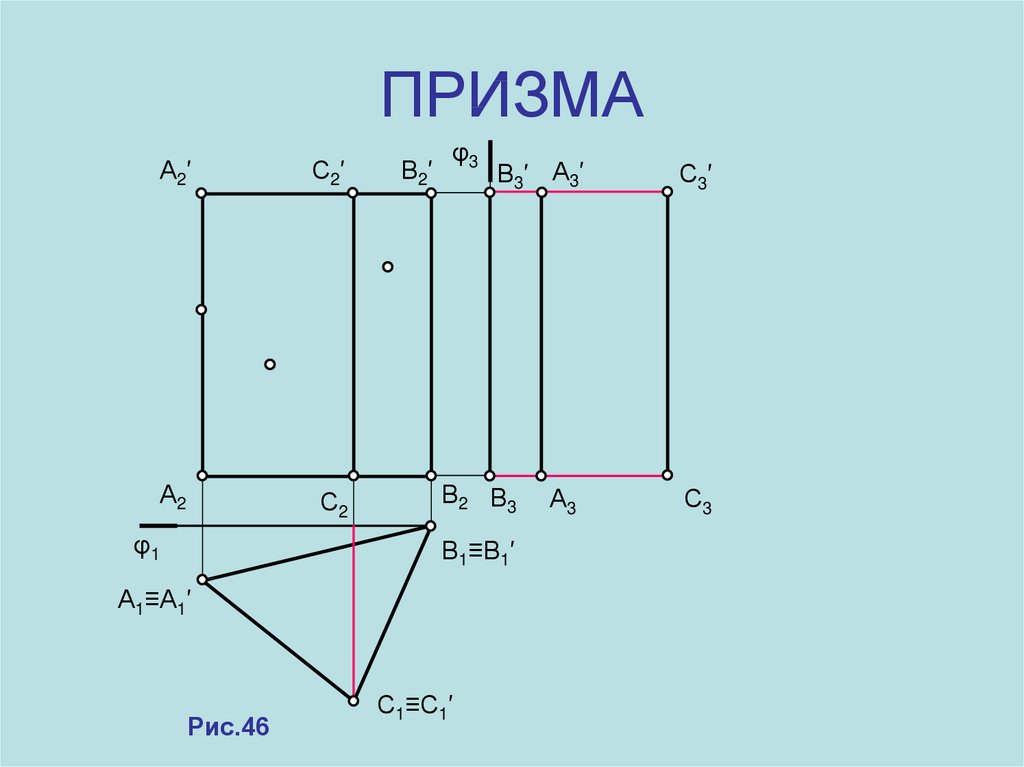
8. ПРИЗМА
А2 ′С2′
А2
С2
φ1
В2′
φ3
В3′ А3′
В2 В3
В1≡В1′
А1≡А1′
Рис.46
С1≡С1′
А3
9. ПРИЗМА
А2 ′С2′
А2
С2
φ1
В2′
φ3
В3′ А3′
В2 В3
В1≡В1′
А1≡А1′
Рис.46
С1≡С1′
А3
С3′
С3
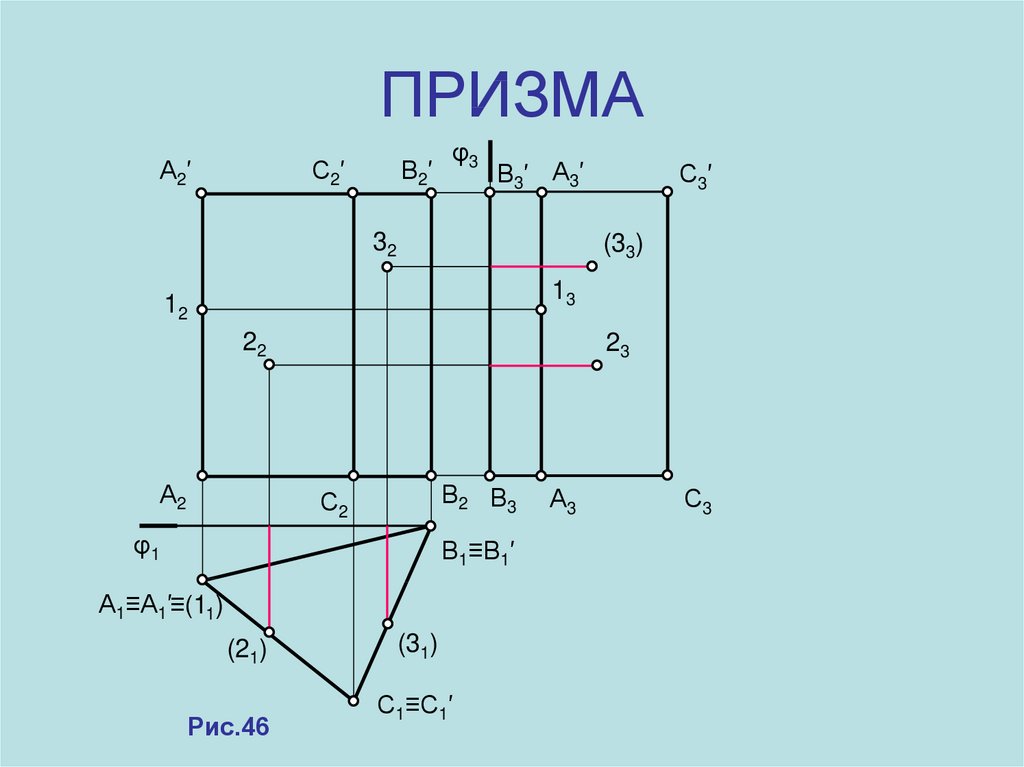
10. ПРИЗМА
А2 ′С2′
В2′
φ3
В3′ А3′
32
С3′
(33)
13
12
22
А2
23
В2 В3
С2
φ1
В1≡В1′
А1≡А1′≡(11)
(21)
Рис.46
(31)
С1≡С1′
А3
С3
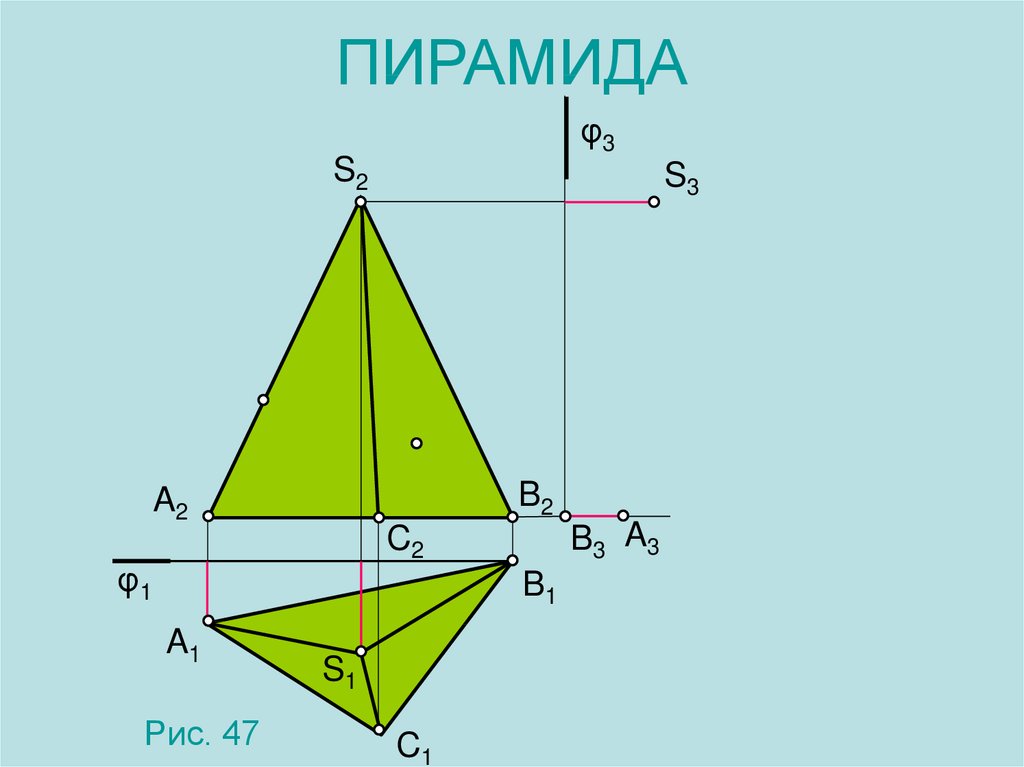
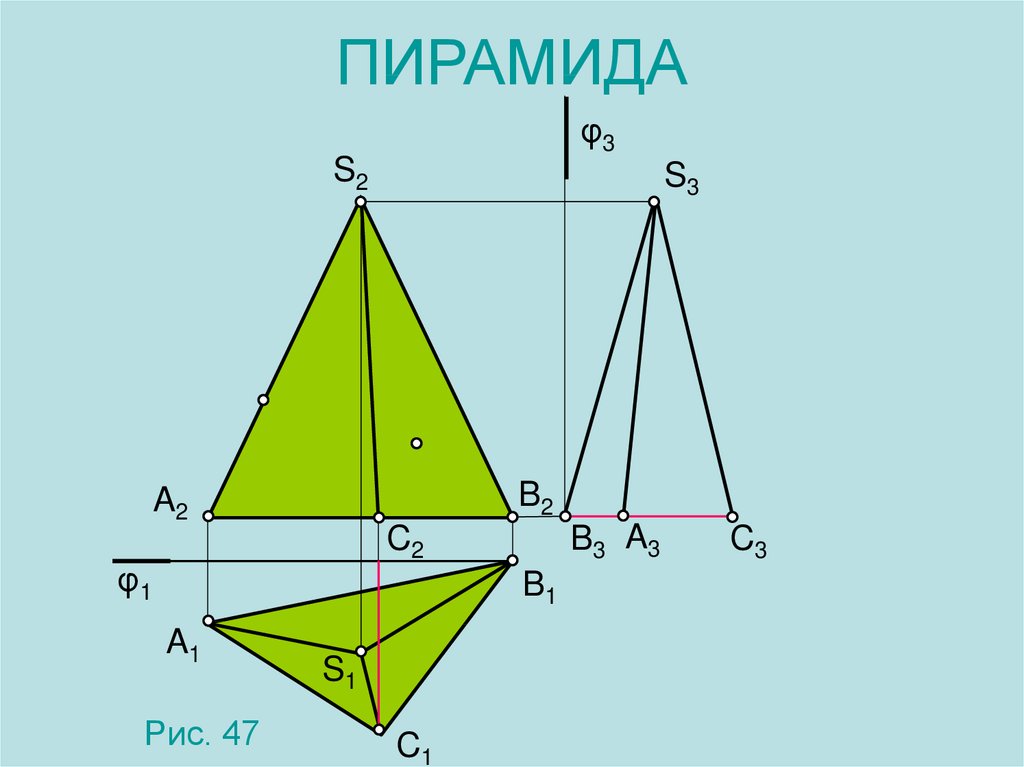
11. ПИРАМИДА
φ3S2
S3
B2
A2
B3 A3
C2
φ1
B1
A1
Рис. 47
S1
C1
12. ПИРАМИДА
φ3S2
S3
B2
A2
B3 A3
C2
φ1
B1
A1
Рис. 47
S1
C1
C3
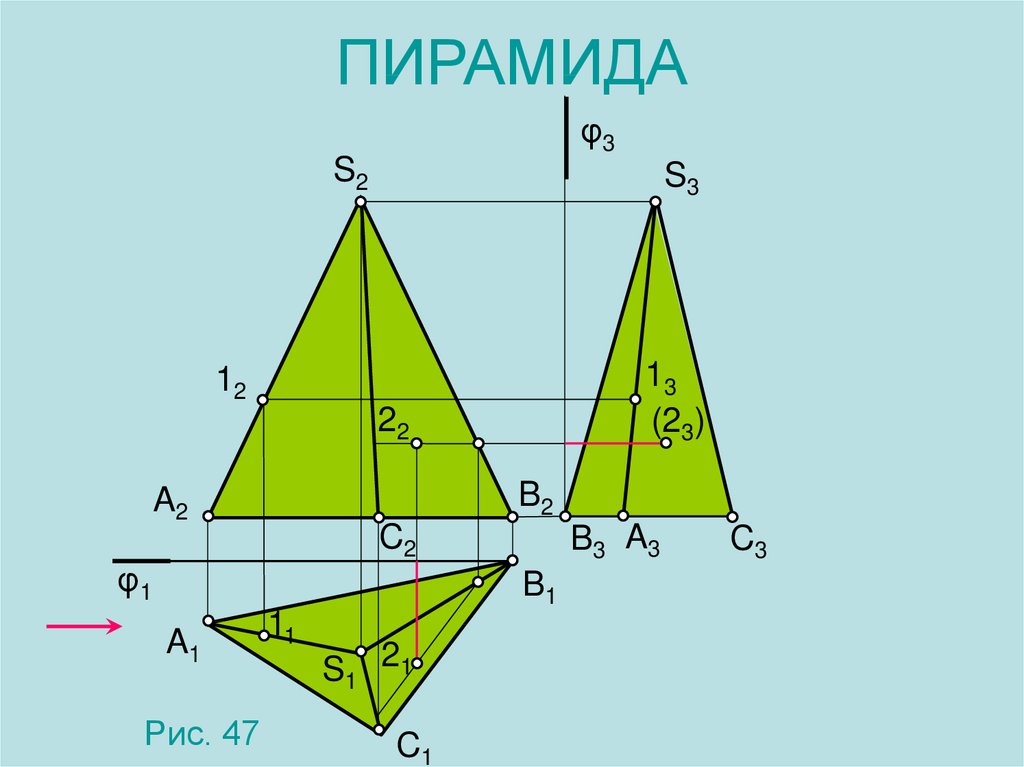
13. ПИРАМИДА
φ3S2
S3
13
(23)
12
22
B2
A2
C2
φ1
B3 A3
B1
A1
Рис. 47
11
S1 21
C1
C3
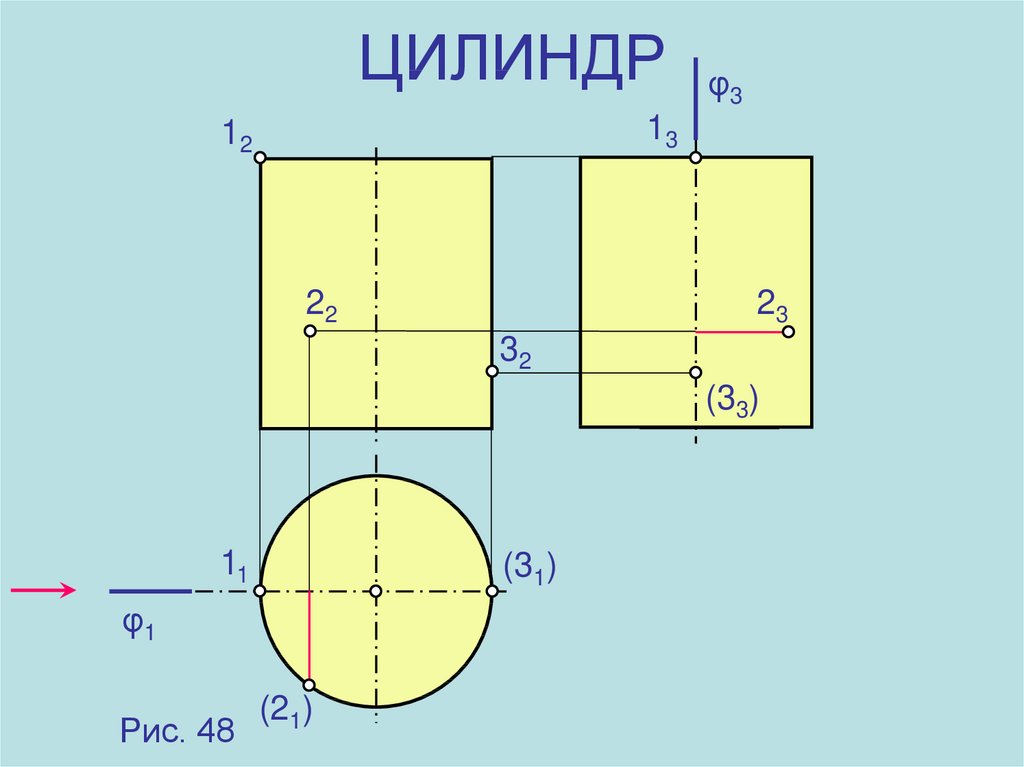
14. ЦИЛИНДР
φ313
12
22
23
32
(33)
11
(31)
φ1
Рис. 48
(21)
15. КОНУС
3222
(33)
23
12
φ3
φ1
21
11
31
Рис. 49
13
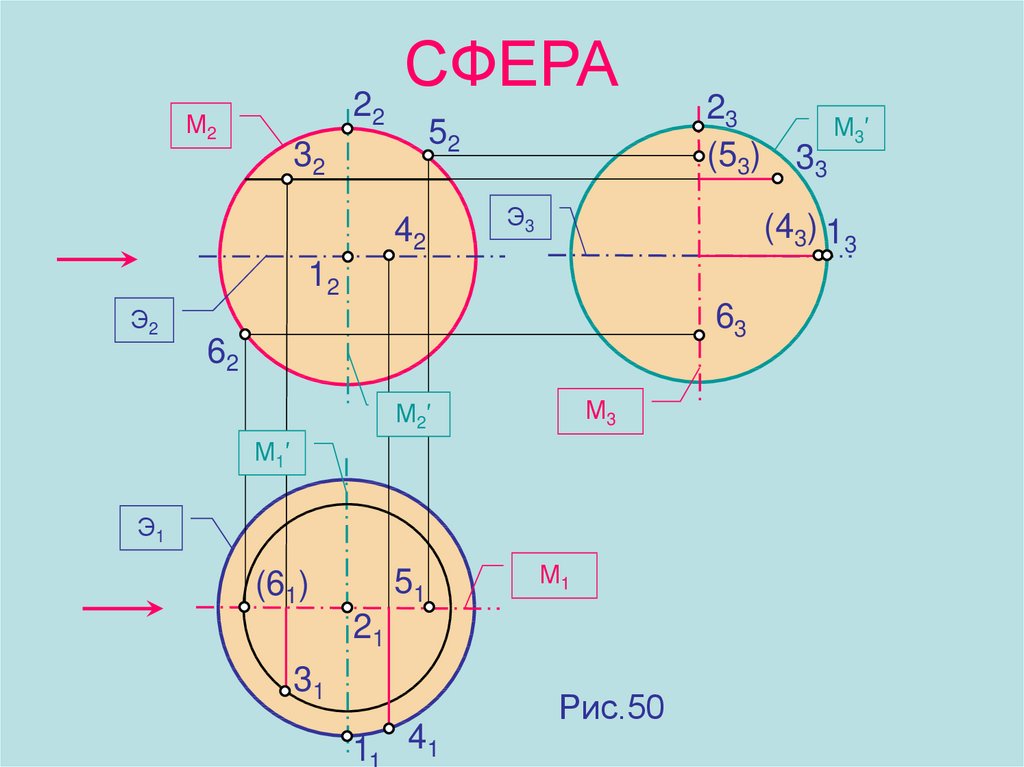
16. СФЕРА
22М2
СФЕРА
52
32
42
23
(53)
Э3
(43) 13
12
Э2
63
62
М3
М2 ′
М1 ′
Э1
51
(61)
М1
21
31
11 41
33
М3 ′
Рис.50




 Инженерная графика
Инженерная графика








