Взаимно-обратные функции

1.

2.

Для обозначения функции, кроме известного вам
y=y(x), часто используют буквы f, g, F
Например , y=f(x)
g(x)=2x-1
F(x)=x2
Независимую переменную х называют – аргументом
Дано:
Дано:
f(x) = 2х + 3
f(x) = 2х + 3, f (х) = 42
Найти:
Найти: х
f (5)
Решение:
Решение:
42 = 2х + 3
f (5) = 2 · 5 + 3 = 13
2х = 39
Ответ: f (5) = 13
х = 19,5
Ответ: x=19,5

3.

Дано:
v(t ) v0 gt
Найти:
t–?
Решение:
v0 gt v
gt v0 v
v0 v
t
g
т.е.
v0 v
t (v )
g
v(t ) v0 gt
v0 v
t (v )
g
Обратимая
функция
Обратная
функция к v( t )

4.

Если функция у = f ( х ) принимает каждое
своё значение у только при одном значении
х, то эту функцию называют
обратимой
Выберите обратимые функции.
1. f(x)=2x-2
2. f(x)=x2
3. f(x)=x2+2
4. f(x)=x3
5. f(x)=x3+5

5.

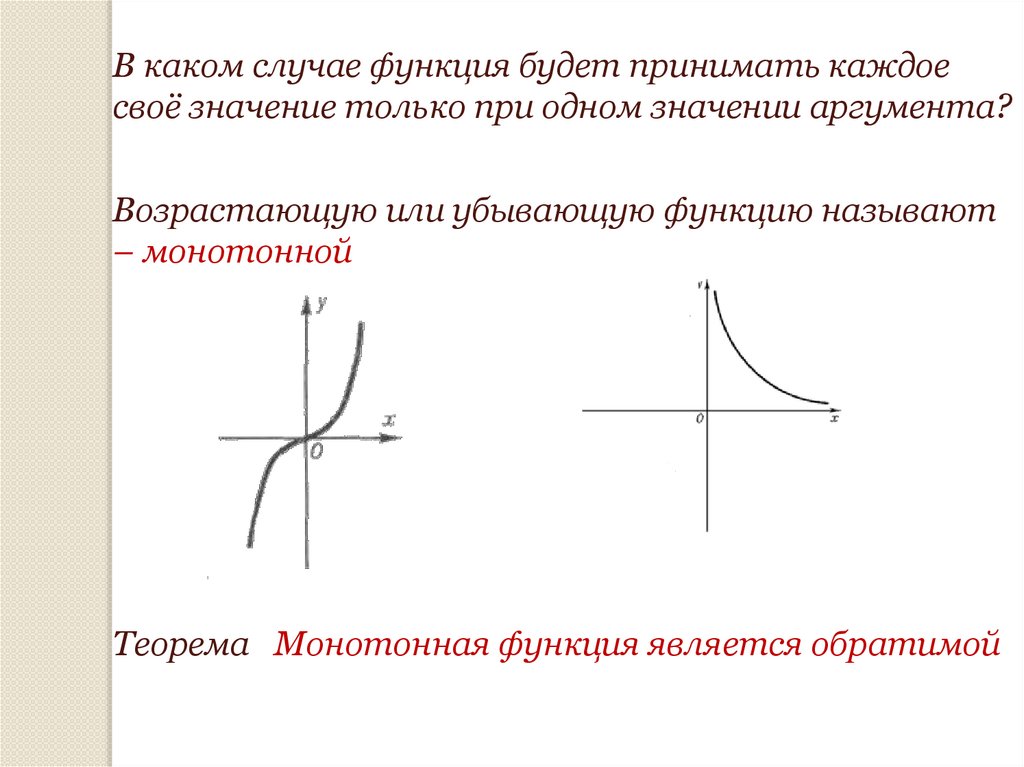
В каком случае функция будет принимать каждое
своё значение только при одном значении аргумента?
Возрастающую или убывающую функцию называют
– монотонной
Теорема Монотонная функция является обратимой

6.

Пусть у = f (x) – обратимая функция. Тогда каждому у
из множества значений функции соответствует одно
определённое число х из области её определения,
такое, что f (x) = y.
Это соответствие определяет функцию х от у, которую
обозначим х = g(y). Поменяем местами х и у: у = g(x).
Функцию у = g (x) называют обратной к функции
у = f (x).

7.

Найти функцию, обратную к функции
y=2x-2
Решаем это уравнение относительно х,
т.е. выражаем х через у
у+2=2х
Меняем местами х и у
Функция
обратна функции y=2x-2

8.

Найти функцию, обратную данной
Решение:
1
у
х 2
1
х 2
у
1
х 2
у
Ответ:
1
у 2
х
у 2
1
x
1
у
х 2

9.

у
у
у
у 2
1
х 2
1
х
2
0
2
х
0
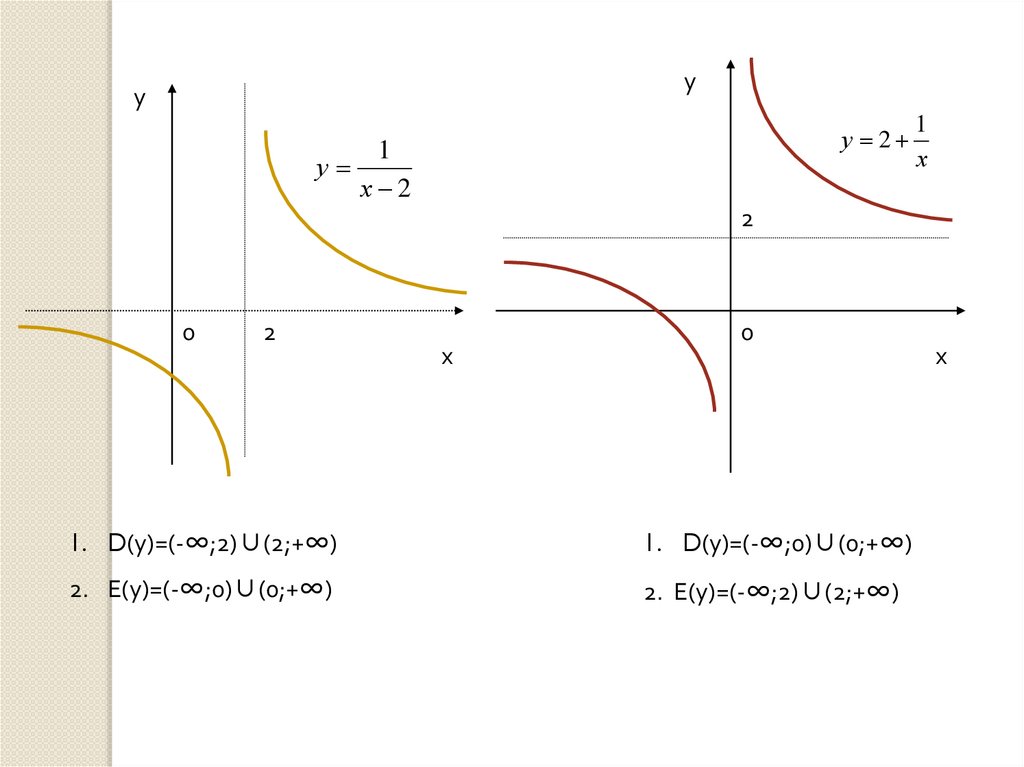
1. D(у)=(-∞;2)∪(2;+∞)
1. D(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;2)∪(2;+∞)
х

10.

1. Область определения обратной функции совпадает
с множеством значений исходной, а множество
значений обратной функции совпадает с областью
определения исходной функции
1. D(у)=(-∞;2)∪(2;+∞)
1. D(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;2)∪(2;+∞)

11.

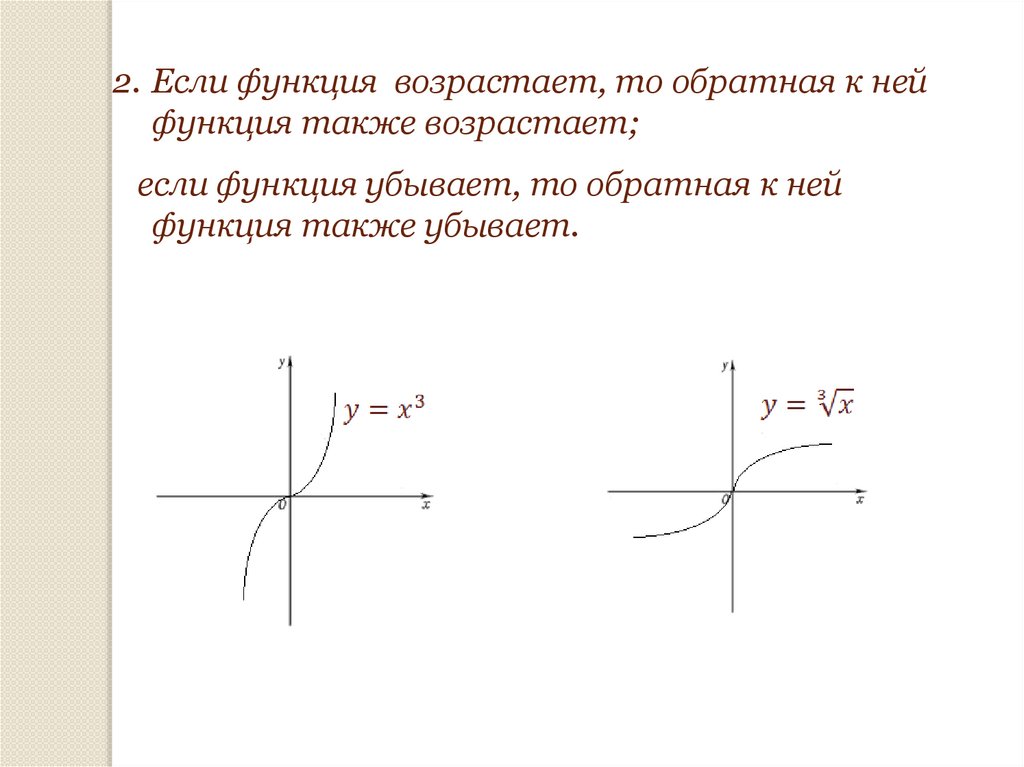
2. Если функция возрастает, то обратная к ней
функция также возрастает;
если функция убывает, то обратная к ней
функция также убывает.

12.

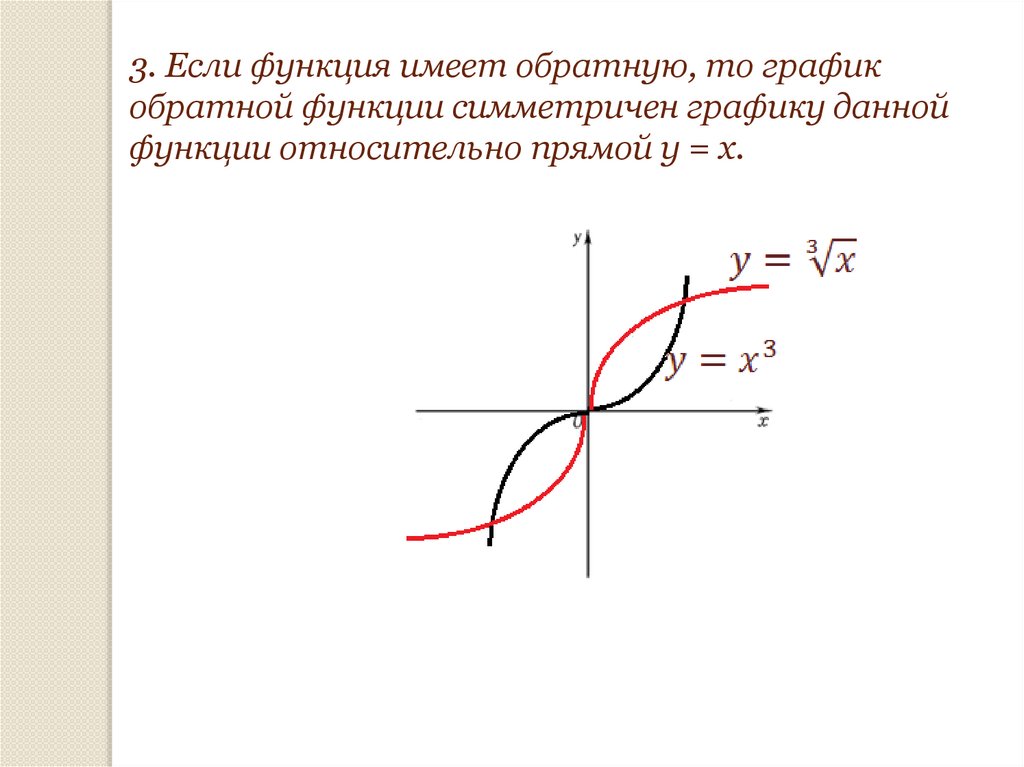
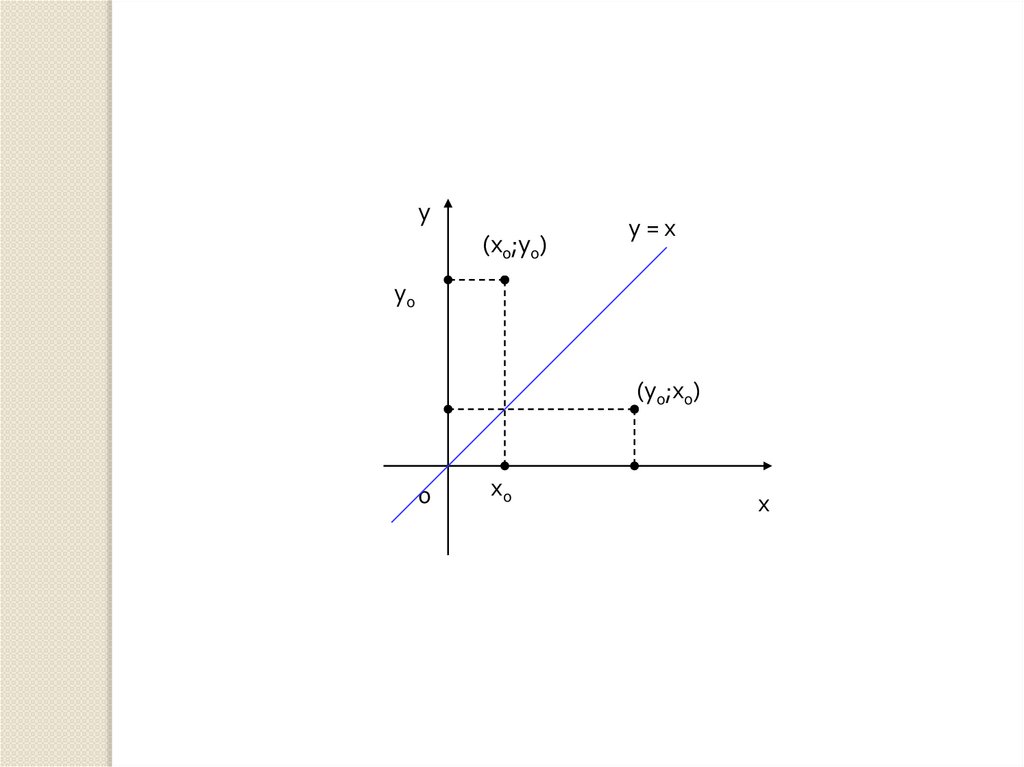
3. Если функция имеет обратную, то график
обратной функции симметричен графику данной
функции относительно прямой у = х.

13.

у
(х0;у0)
у=х
у0
(у0;х0)
0
х0
х

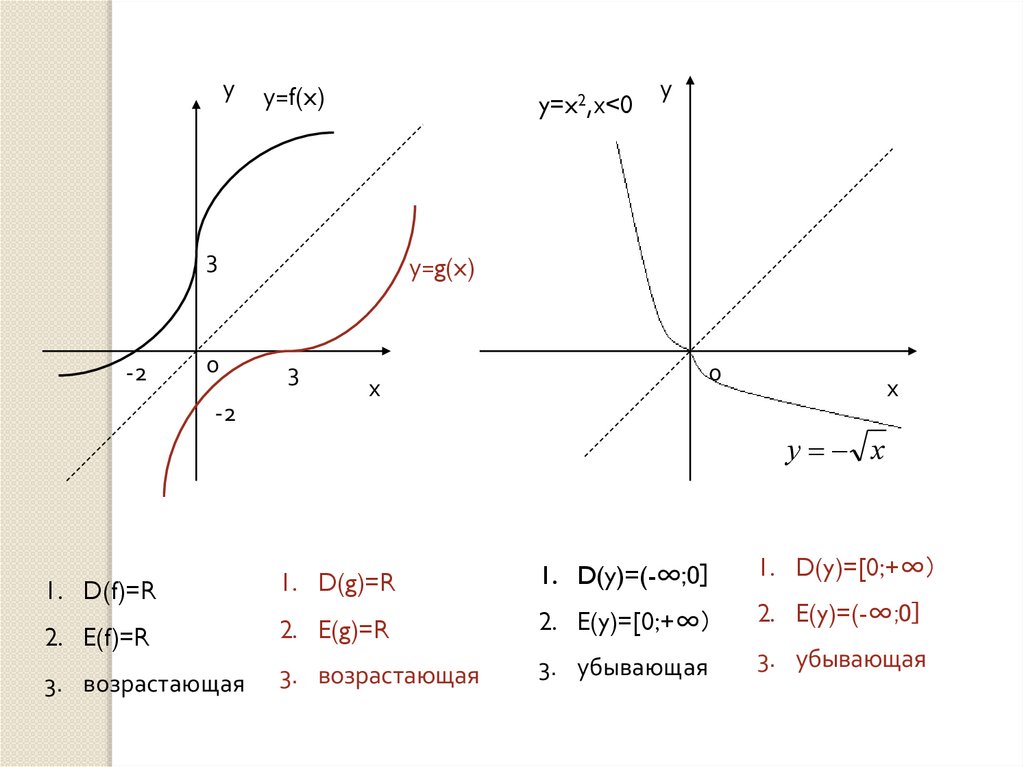
14.

у
у=f(x)
y=x2,х<0
3
-2
0
-2
у
у=g(x)
3
0
х
х
у х
1. D(f)=R
1. D(g)=R
1. D(y)=(-∞;0]
1. D(y)=[0;+∞)
2. E(f)=R
2. E(g)=R
2. E(y)=[0;+∞)
2. E(y)=(-∞;0]
3. возрастающая
3. возрастающая
3. убывающая
3. убывающая

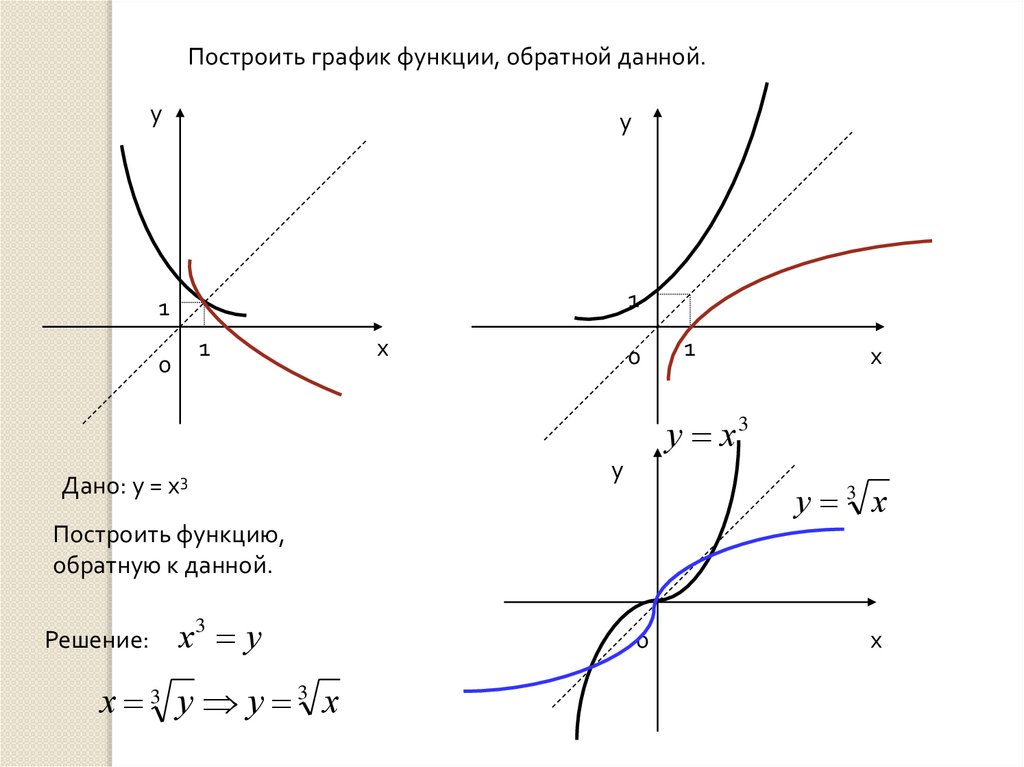
15.

Построить график функции, обратной данной.
у
у
1
1
1
0
х
0
1
х
у х3
Дано: у = х3
у
у 3 х
Построить функцию,
обратную к данной.
Решение:
х3 у
х 3 у у 3 х
0
х