Похожие презентации:
Взаимно-обратные функции. Функция - соответствие
1.
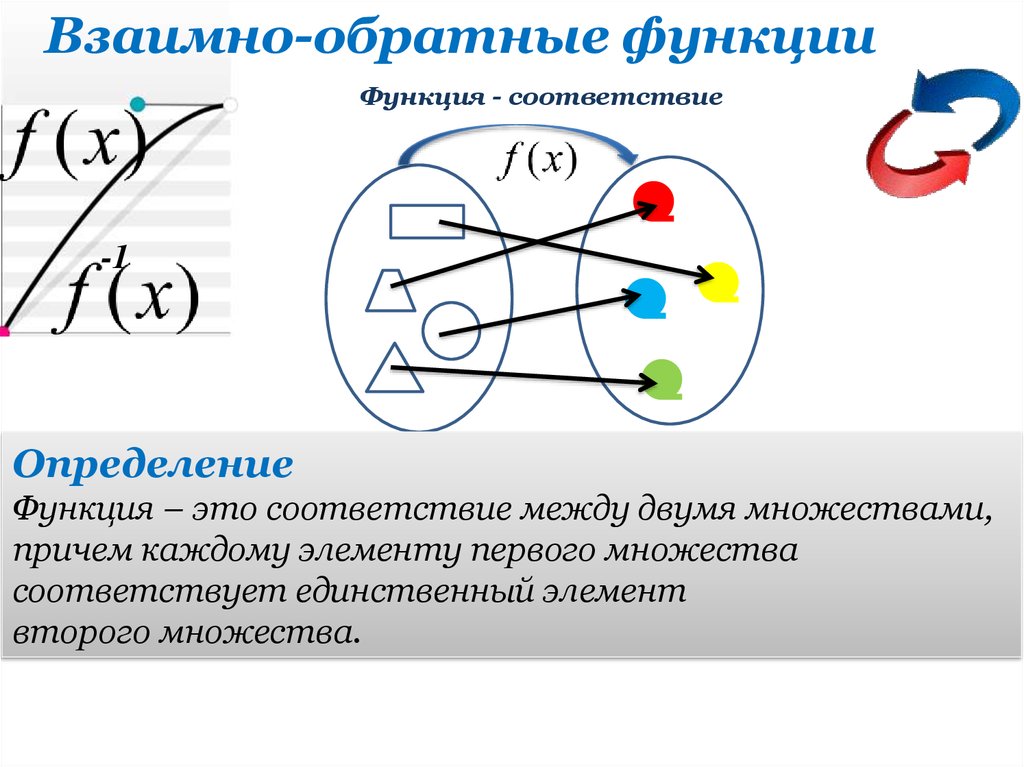
Взаимно-обратные функцииФункция - соответствие
-1
Область определения
Определение
функции
Множество значений
функции
Функция – это соответствие между E(f)=Y
двумя множествами,
D(f)=X
причем каждому элементу первого множества
соответствует
единственный
элемент
D(f)={
}
E(f)={
}
второго множества.
2.
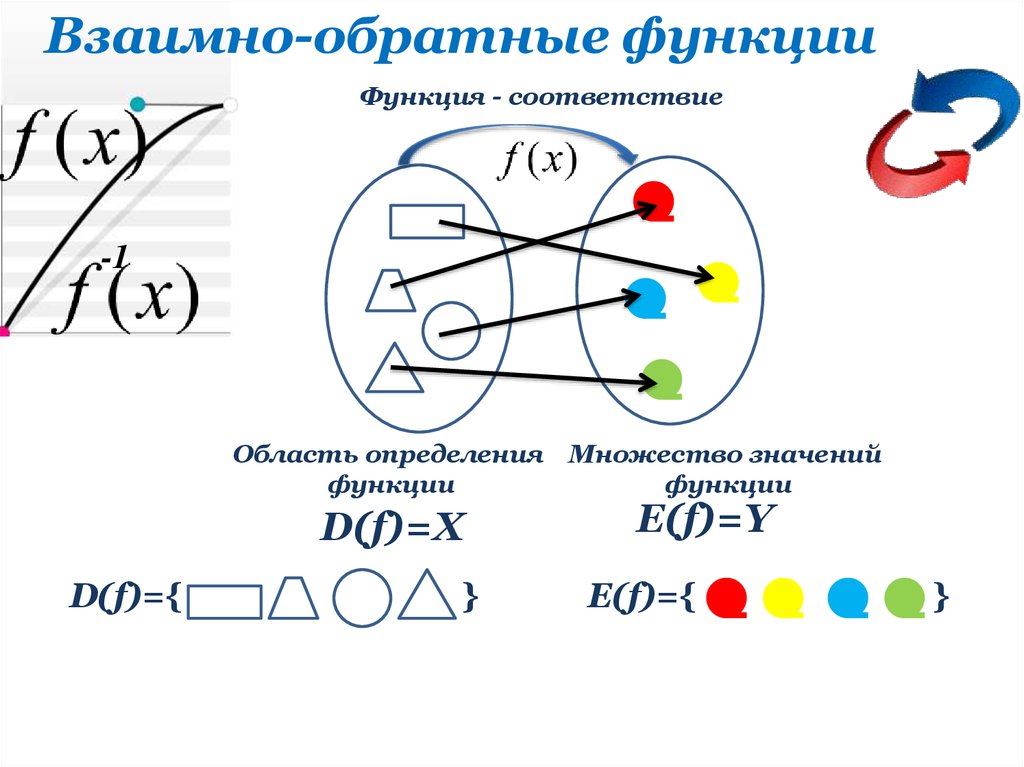
Взаимно-обратные функцииФункция - соответствие
-1
Область определения Множество значений
функции
функции
D(f)=X
D(f)={
}
E(f)=Y
E(f)={
}
3.
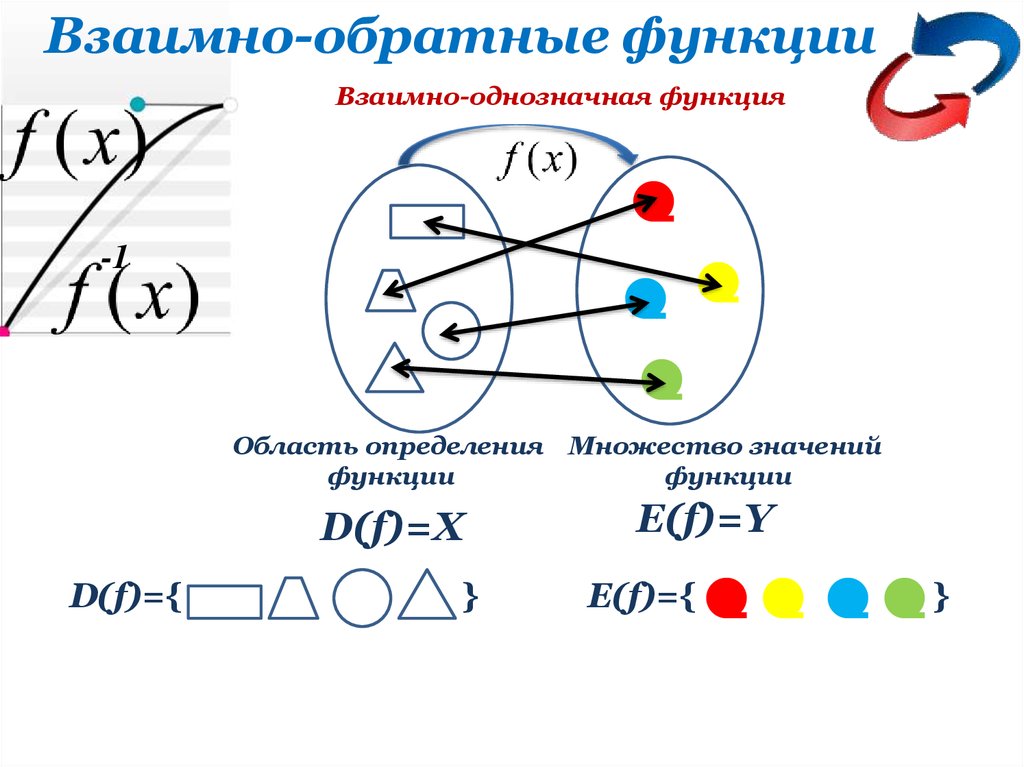
Взаимно-обратные функцииВзаимно-однозначная функция
-1
Область определения Множество значений
функции
функции
D(f)=X
D(f)={
}
E(f)=Y
E(f)={
}
4.
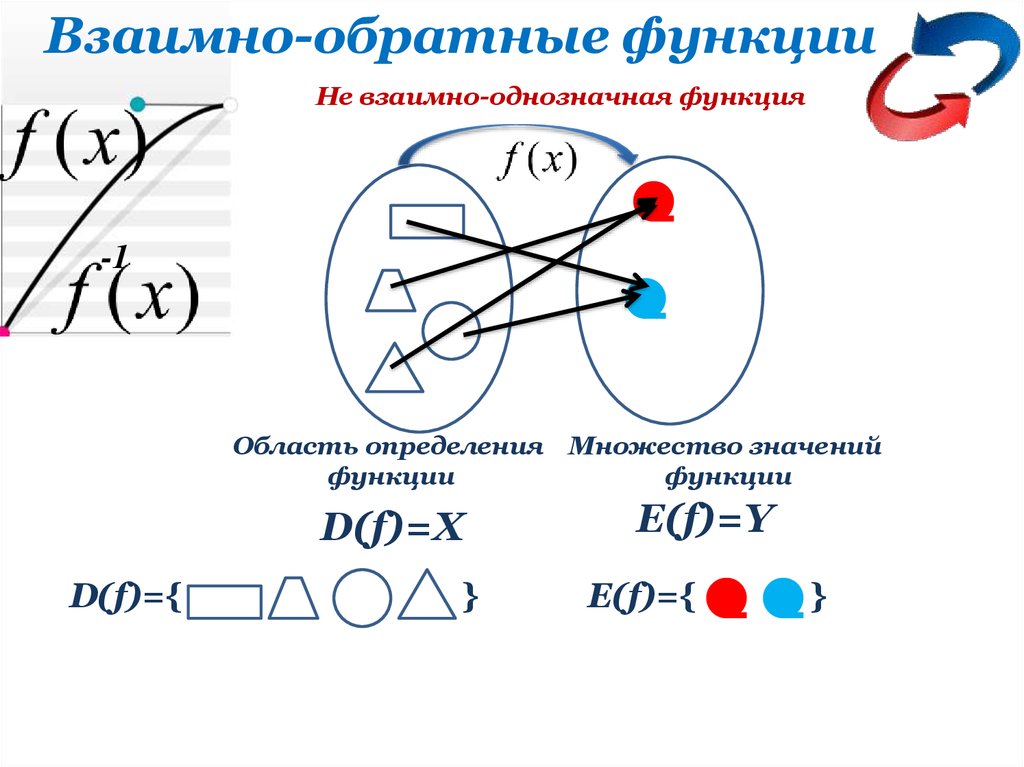
Взаимно-обратные функцииНе взаимно-однозначная функция
-1
Область определения Множество значений
функции
функции
D(f)=X
D(f)={
}
E(f)=Y
E(f)={
}
5.
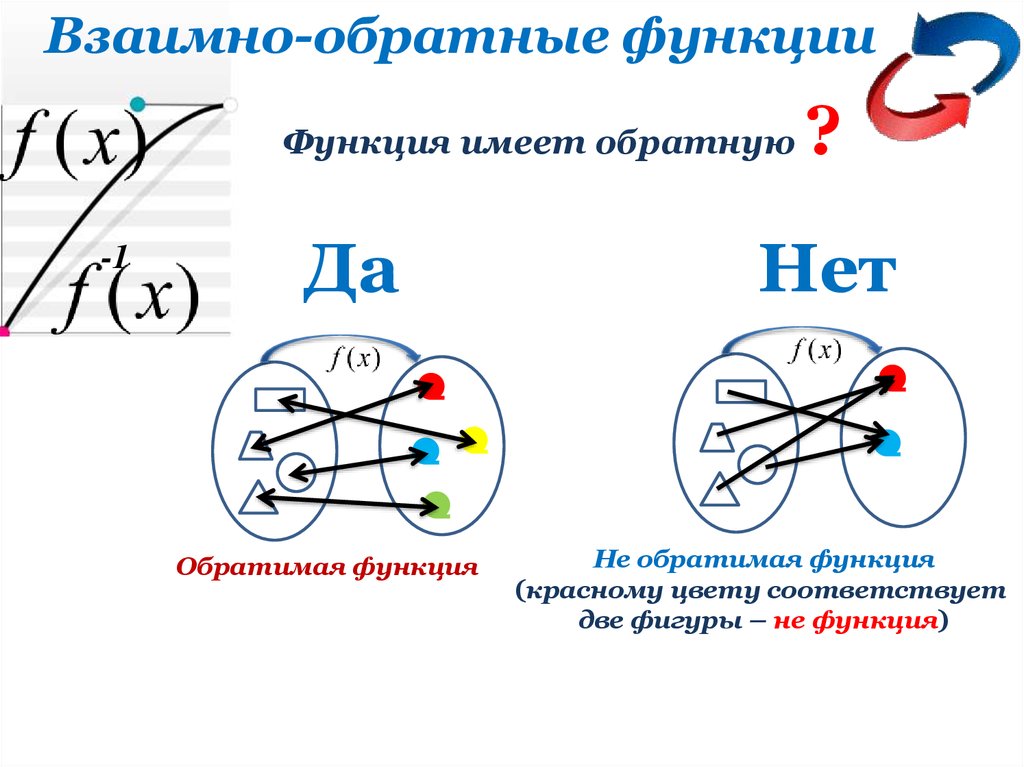
Взаимно-обратные функцииФункция имеет обратную
-1
Да
Обратимая функция
?
Нет
Не обратимая функция
(красному цвету соответствует
две фигуры – не функция)
6.
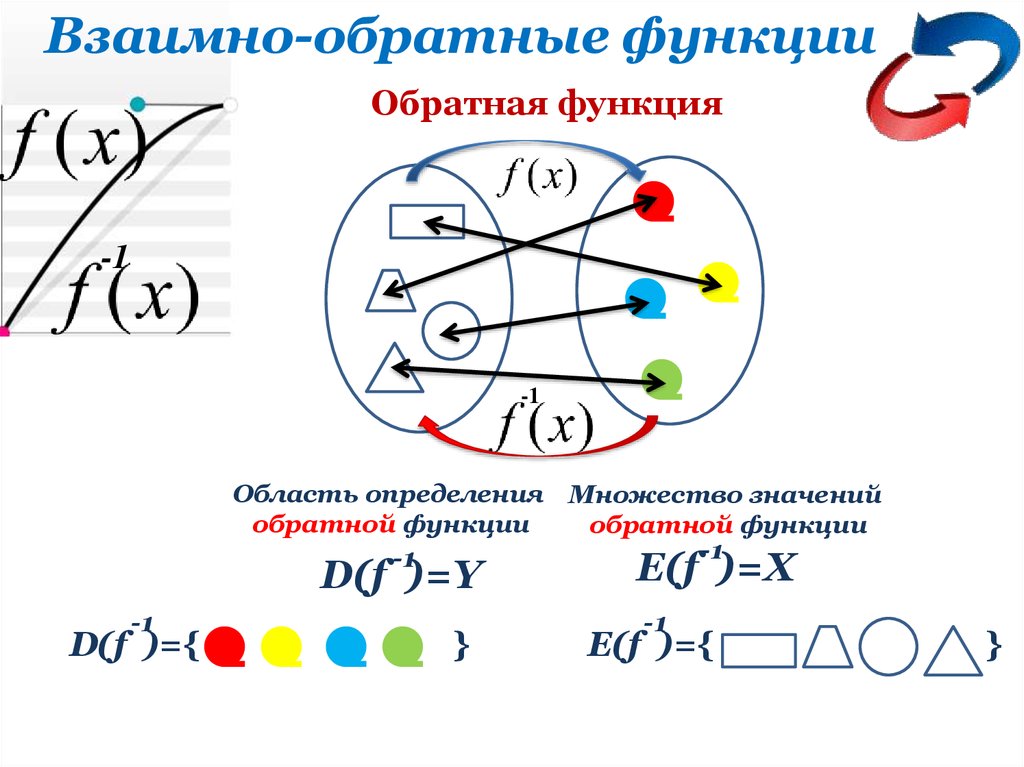
Взаимно-обратные функцииОбратная функция
-1
-1
Область определения Множество значений
обратной функции
обратной функции
-1
-1
D(f )=Y
-1
D(f )={
}
E(f )=X
-1
E(f )={
}
7.
Взаимно-обратные функцииДана функция y=f(x)
Как найти обратную
?
-1
Определение
Функция f называется обратимой, если для любых
двух различных чисел х1 и x2, принадлежащих D(f),
числа f(x1) и f(x2) также различны.
Определение
Функция g(x) называется обратной для функции f(x),
если для x из E(f), верно равенство f((g(x))=x
8.
Взаимно-обратные функцииДана функция y=f(x)
?
-1
Как найти обратную
1) Переобозначить x и y x=f(y)
2) Выразить y через x
-1
Получили обратную функцию y=f (x)
Пример: Найти функцию, обратную y=2x+6
1) x=2y+6
2) -2y=-x+6
3) y=0,5x+3 – обратная функция


 Математика
Математика








