Похожие презентации:
Взаимно обратные функции
1.
«Взаимно обратные функции»для 10 класса
2.
yy=
f(x)
E( f )
0
х
D( f)
x
Если каждому значению х из
некоторого
множества
действительных
чисел
поставлено в соответствие по
определённому правилу f число
у, то, говорят, что на этом
множестве определена функция.
3.
Укажите область определения даннойна графике функции
D(y)=(- :0)U(0;+ )
4.
Укажите область определения даннойна графике функции
D(y)=[-4;2]
5.
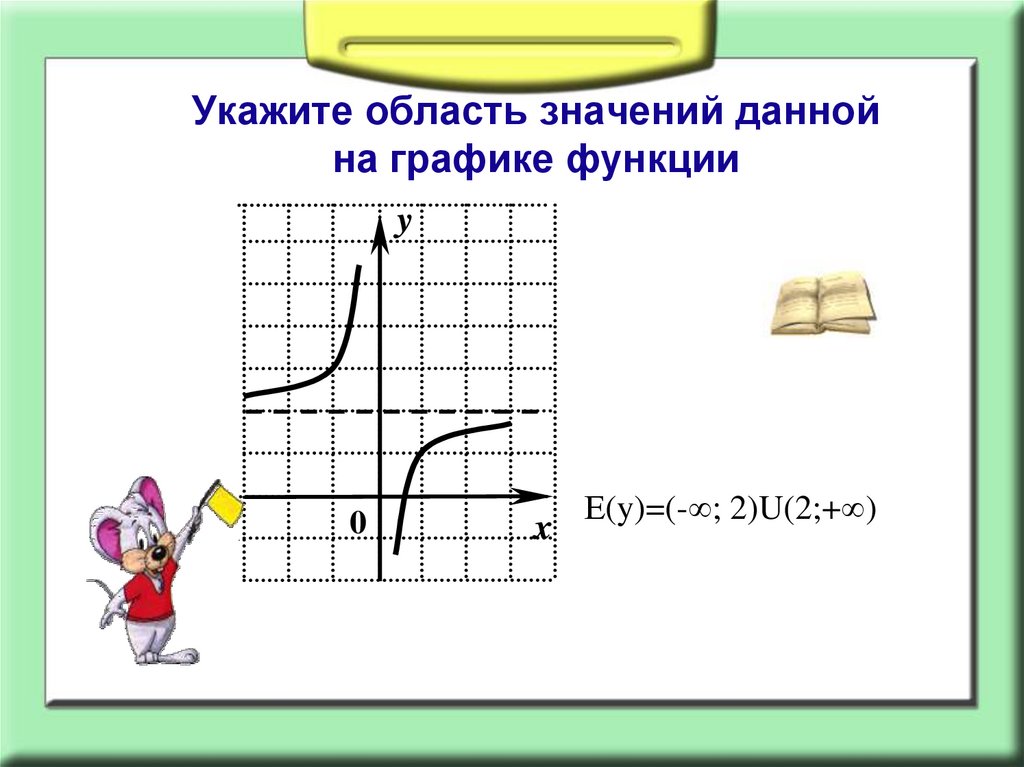
Укажите область значений даннойна графике функции
y
0
x
Е(y)=(- ; 2)U(2;+ )
6.
Понятие обратной функции7.
Рассмотрим функцию зависимости скоростидвижения тела, брошенного вверх с начальной
скоростью 0 от времени движения t
• Дано:
v(t ) v gt
Обратимая функция
0
Найти: t -?
Решение:
v0 gt v
gt v0 v
v0 v
t
g
, т.е.
v0 v
t (v )
g
Обратная функция к v(
t)
8.
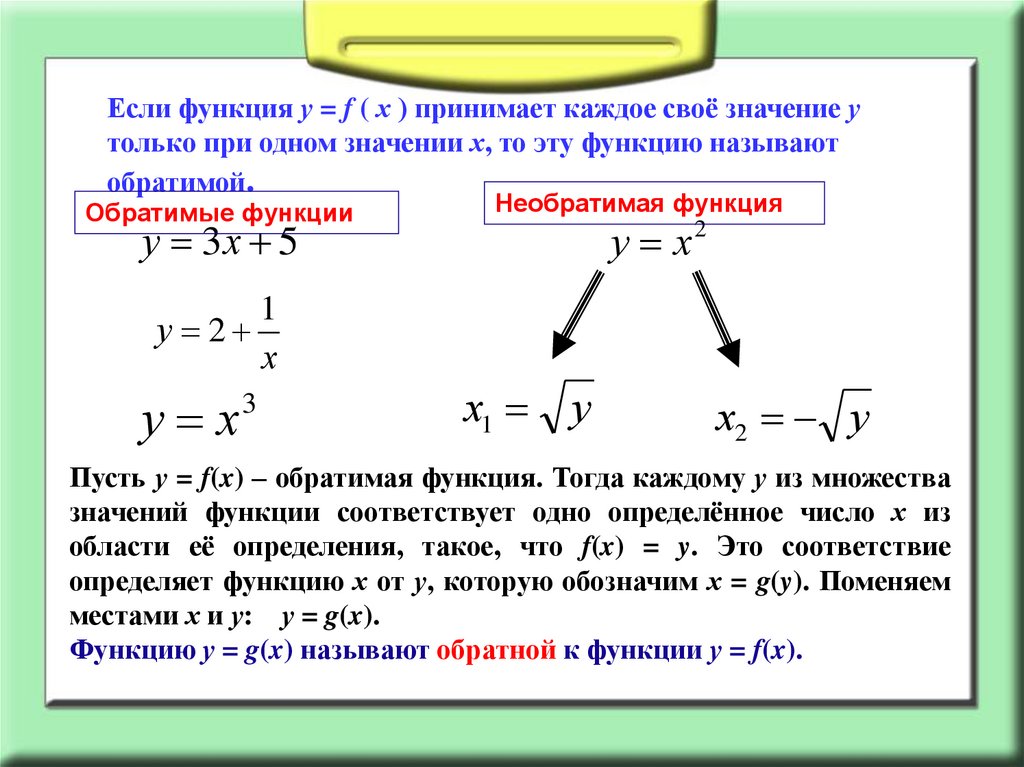
Если функция у = f ( х ) принимает каждое своё значение утолько при одном значении х, то эту функцию называют
обратимой.
Обратимые функции
у 3х 5
Необратимая функция
у х2
1
у 2
х
у х
3
х1 у
х2 у
Пусть у = f(x) – обратимая функция. Тогда каждому у из множества
значений функции соответствует одно определённое число х из
области её определения, такое, что f(x) = y. Это соответствие
определяет функцию х от у, которую обозначим х = g(y). Поменяем
местами х и у: у = g(x).
Функцию у = g(x) называют обратной к функции у = f(x).
9.
Найти функцию, обратную даннойДано:
1
у
х 2
у = g(x)
(1)
Решение:
1
у
х 2
х 2
х 2
Ответ:
1
у
1
у
у 2
у 2
1
x
1
х
(2)
Если функция (2) обратна к функции (1), то такие функции
называют взаимно-обратными.
10.
Практический приём нахождения формулы функции,обратной к функции y=f(x)
Алгоритм
Пример
11.
Примеры решения задачНайдите функцию, обратную к функции
Решение
Комментарий
12.
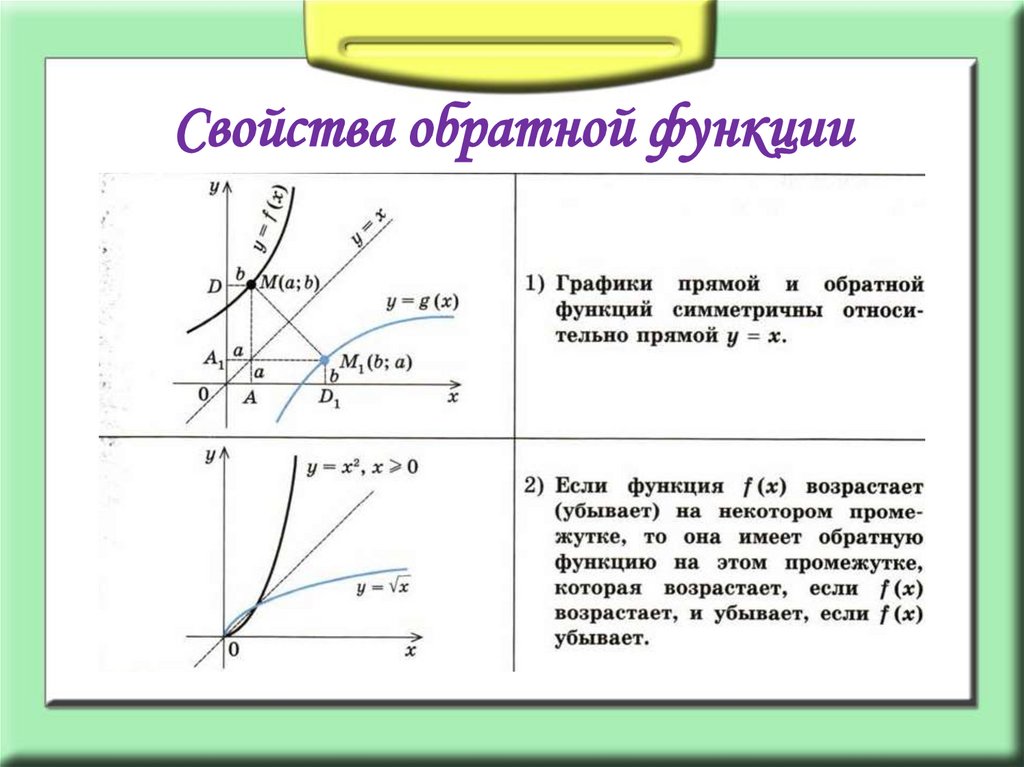
Свойства обратной функции13.
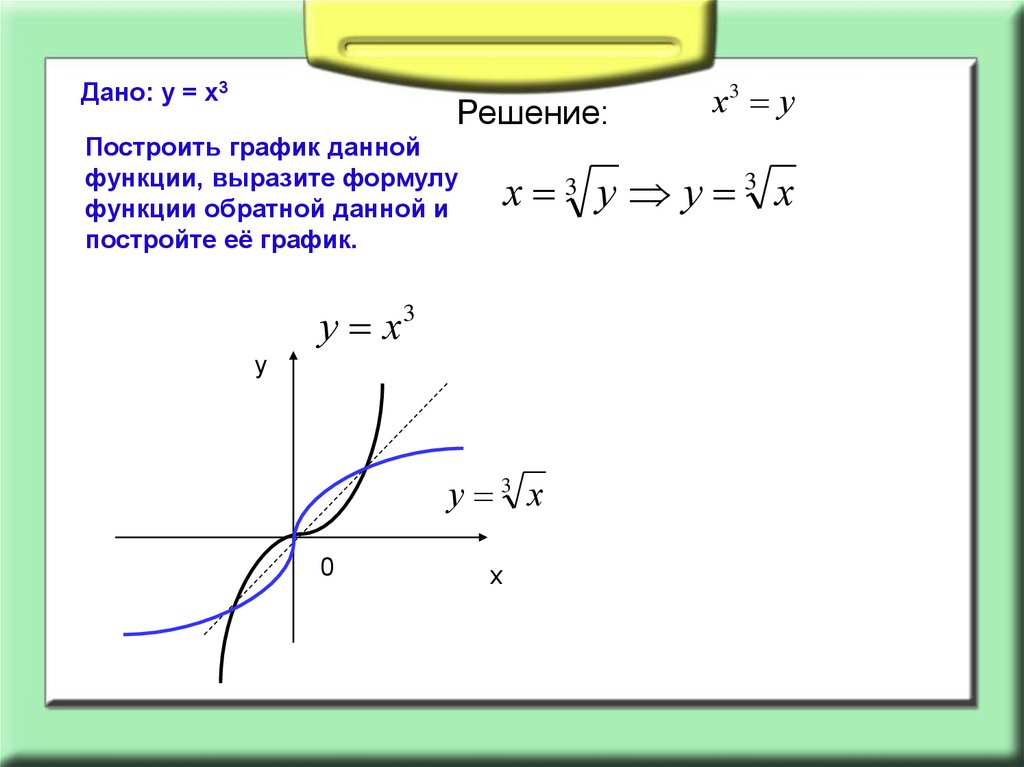
Дано: у = х3Решение:
Построить график данной
функции, выразите формулу
функции обратной данной и
постройте её график.
х 3 у у 3 х
у х3
у
у 3 х
0
х3 у
х
14.
уу=f(x)
y=x2,х<0
у=g(x)
3
-2
0
у
3
х
0
х
-2
у х
1. D(f)=R
1. D(g)=R
2. E(f)=R
2. E(g)=R
3. возрастающая 3. возрастающая
1. D(y)=(-∞;0] 1. D(y)=[0;+∞)
2. E(y)=[0;+∞) 2. E(y)=(-∞;0]
3. убывающая 3. убывающая
15.
данной.у Построить график функции, обратной
у
1
1
0
1
х
0
1
х
16.
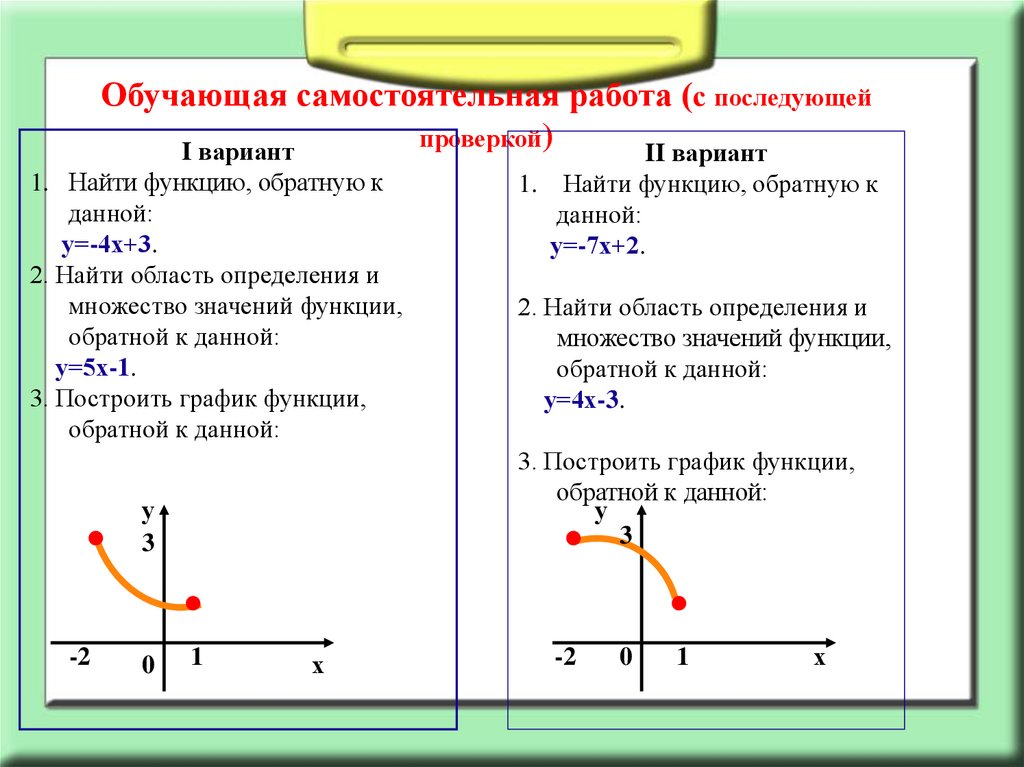
Обучающая самостоятельная работа (с последующейпроверкой)
I вариант
II вариант
1. Найти функцию, обратную к
данной:
у=-4х+3.
2. Найти область определения и
множество значений функции,
обратной к данной:
у=5х-1.
3. Построить график функции,
обратной к данной:
.
-2
у
3
0
1. Найти функцию, обратную к
данной:
у=-7х+2.
2. Найти область определения и
множество значений функции,
обратной к данной:
у=4х-3.
3. Построить график функции,
обратной к данной:
у
3
.
.
1
х
-2
.
0
1
х
17.
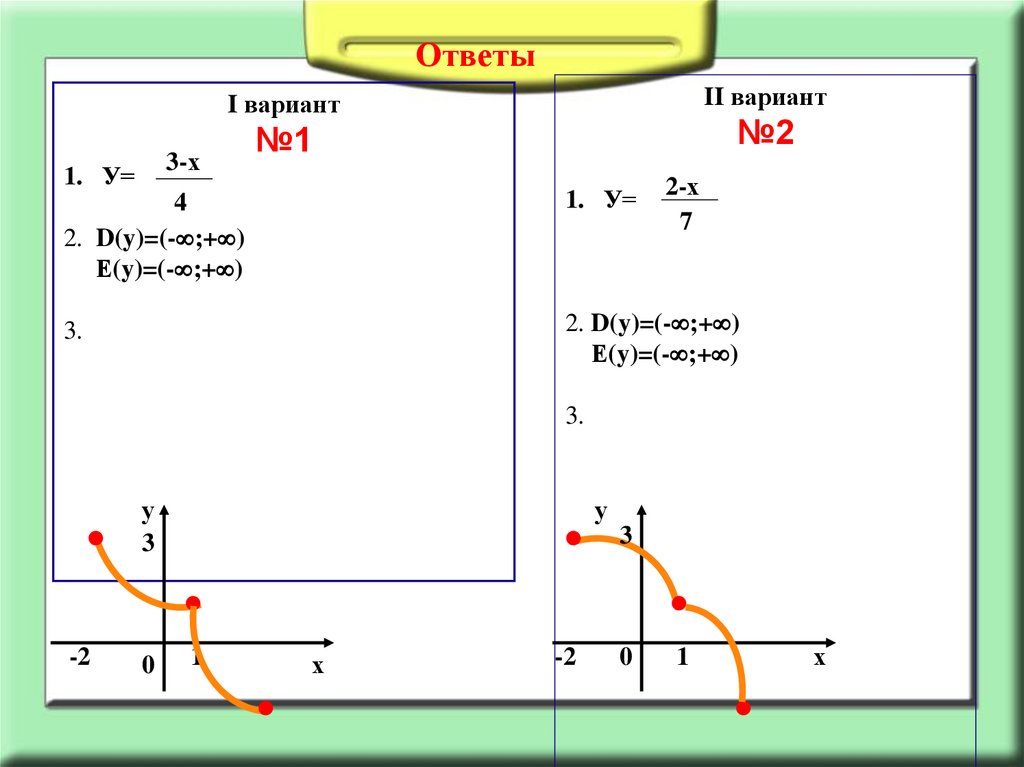
ОтветыII вариант
I вариант
3-х
1. У=
№2
№1
2-х
7
4
2. D(y)=(- ;+ )
Е(y)=(- ;+ )
1. У=
3.
2. D(y)=(- ;+ )
Е(y)=(- ;+ )
3.
.
-2
у
3
0
.
.
1
.
х
-2
у
3
.
0
1
.
х
18.
Выполнить заданияи прислать 23 ноября до 19.00












 Математика
Математика








