Регулярные возмущения в дифференциальных уравнениях. (Лекция 5)

1. Введение в асимптотические методы. Лекция 5

Регулярные возмущения в
дифференциальных уравнениях

2. 1. Регулярные возмущения

К сожалению, немногие возмущения ДУ регулярны
Работать с регулярными возмущениями просто:
применимы “очевидные” разложения
Задачи могут быть возмущены в
уравнении
граничных условиях
положении границы
просто
чуть сложнее
Далее приводятся всего 2 примера регулярно
возмущенных задач, оба с возмущением в
положении границы

3. 2. Полиномы Лежандра

Сферические
координаты
1 2 u
1
u
u (r , ) 2
r
2
sin
r r r r sin
Ищем решение вида
u
r
Задача на
собственные
значения
n
r n 1
u n r n
d n
1 d
sin
0
sin d
d
dP ( y )
d
n(1 n) Pn ( y ) 1 y 2 n
0
dy
y
n(1 n) n
y cos
n Pn cos
Задача на собственные значения имеет решения при n=1,2,….
Собственные функции - полиномы Лежандра
P0 y 1, P1 y y, P2 y
3 2 1
y ,
2
2

4. 3. Полиномы Лежандра

Система полиномов Лежандра полна и ортогональна
1
dP ( y )
d
n(1 n) Pn ( y ) 1 y 2 n
0
dy
y
1
-
n(1 n) Pn ( y ) Pm ( y )dy
1
1
m(1 m) Pn ( y ) Pm ( y )dy
1
Pm ( y )
dy
1
1
1 y P ( y) P ( y)dy
2
n
m
1
1
1 y P ( y) P ( y)dy
2
n
m
1
1
ортогональность
P ( y) P ( y)dy 0,
n
m
n m
1
u (r , ) 0, r 1
r 1: u f ( )
u (r , ) 0, r 1
r 1: u f ( )
f ( ) an Pn (cos )
n 0
u an Pn (cos ) r n
n 0
u an Pn (cos ) r n 1
n 0

5. 4. Потенциал вокруг близкого к сфере тела

u 1
u (r , ) 0
r 1 P2 cos
С точностью O 2
эллипсоид вращения того же объема,
что и сфера радиуса 1.
u u0 r, u1 r, 2u2 r,
Граничное
условие
1 u r 1 P u r 1 P2
u
u0 r 1 u1 r 1 P2 0
r
2
u
r
P2 2u
2
r 1
2
u1
u
P
2 r 1 2
r
r 1
2
r
2
r 1
P22 2u0
2 r 2
r 1
r 1

6. 5. Потенциал вокруг близкого к сфере тела

0
1
2
u0 0 r 1
u0 1, 1
u1 0 r 1
u0
u1 1, P2
r
u0
u1
P2 cos
1
r
P2 cos
r2
r 1
u2 0 r 1
u2 1, 2P22 cos
u2
36 P4 cos
35r
5
4 P2 cos
7r 3
4
2
36
P
P
P
35 4
7 2
5 0
Эл. емкость C 4 коэффициент при r
1
4 1 52 2
2
5r

7. 6. Форма медленно вращающегося гравитационного жидкого тела

r R ;
u u0 r, 2u1 r, ,
1 r 1
u0
0 r 1
u0 0, u1 0
1 r R
u
0 r R
u, u / n непрерывны при r R
u 0
r
(свободная
1
2 2
2
–
r R:
u 2 r sin Const поверхность
эквипотенциаль)
4
(условие нормировки)
r R dV 3
асимптотическое разложение
R 1 2 R1
0 r 1
уравнение
u1
0 r 1
поведение на бесконечности
r
R ( ) sin d 0
1
0
нормировка

8. 7. Форма медленно вращающегося гравитационного жидкого тела

u r R
u0
u
2
u r 1 R1
u0 r 1 u1 r 1 R1
r r 1
r
u
n r R
1 dR 2
1
R
d
2
u
0
r
1/ 2
r 1
u 1 dR u
2
r R d r R
u1
r
r 1
2
2 u0
R1 2
r
r 1
dR u
1 0
d
r 1
4
O
r 1
u0 r 1 0, u1 r 1 0, u0 / r r 1 0, u1 / r r 1 R1 2u0 / r 2 r 1
u0 r 1 Const,
u0
1 2
u
R
sin Const,
1
1
r
2
r 1
непрерывность
эквипотенциальность

9. 8. Форма медленно вращающегося гравитационного жидкого тела

0 :
2 :
1 r 1
u0
0 r 1
u0 r 1 u0 / r r 1 0
u1 r 0
u1 0
u0 r 0
16 r 2 12 r 1
u0 1 1
r 1
3 r
u0 r 1 Const
u1 r 1 0 u1 / r r 1 R1 R1 ( ) sin d 0
0
u1 r 1 13 R1 12 sin 2 Const= 13 P2 (cos ) Const
R1 aP2 cos
r 2 P2 cos
r 1
u1 c 3
r P2 cos r 1
1
5
c , a
2
2
1
1
5c a, c a
3
3
Rэкв Rпол 2 R1 ( / 2) R1 (0)
15 2
4

10. 9. Приложение к Земле

Считаем, что Земля жидкая (?) и однородная (??)
*
*
Rэкв
Rпол
21 км, R* 6400км
Известно, что
Какова должна быть скорость вращения Земли, чтобы факты соответствовали
нашей теории?
*
*
Rэкв
Rпол
15 2
4 21
2
8.75 10 4
*
R
4
15 6400
Выразим безразмерную величину через угловую скорость вращения
Земли и ускорение свободного падения g
* 2
*
R
gR
*
Поведение истинного гравитационного потенциала на u g *
r
r
1
Поведение безразмерного гравитационного потенциала на
u
3r
*
Истинные потенциалы в задаче нормированы на 3gR
Центробежные силы
T
2
27.5 час
r R
1
2
1
2
2
*
r
2
* 2
* 2
sin 2
sin 2
2
2 R*
3g
3g
5 -1
6.34
10
c
*
R

11. 10. Возмущения в уравнениях: пример

dy
0 y 1:
y y 2 x,
dx
y (1) 1
y y0 y1
y0 y0 x,
y1 y1 y x 1 e
2
0
1 x 2
y0 (1) 1
,
y0 x 1 e1 x
y1 (1) 0 y1 x 2 4 x 5 x 2 2 x e1 x e 2(1 x )
y x 1 e1 x x 2 4 x 5 x 2 2 x e1 x e2(1 x )
Полученное разложение равномерно пригодно на интервале x 0,1
x 1, то разложение не равномерно пригодно
1
Оно разваливается при больших x
Если интересует
Что делать в этой ситуации мы обсудим на следующей лекции, когда
будем рассматривать сингулярно возмущенные задачи

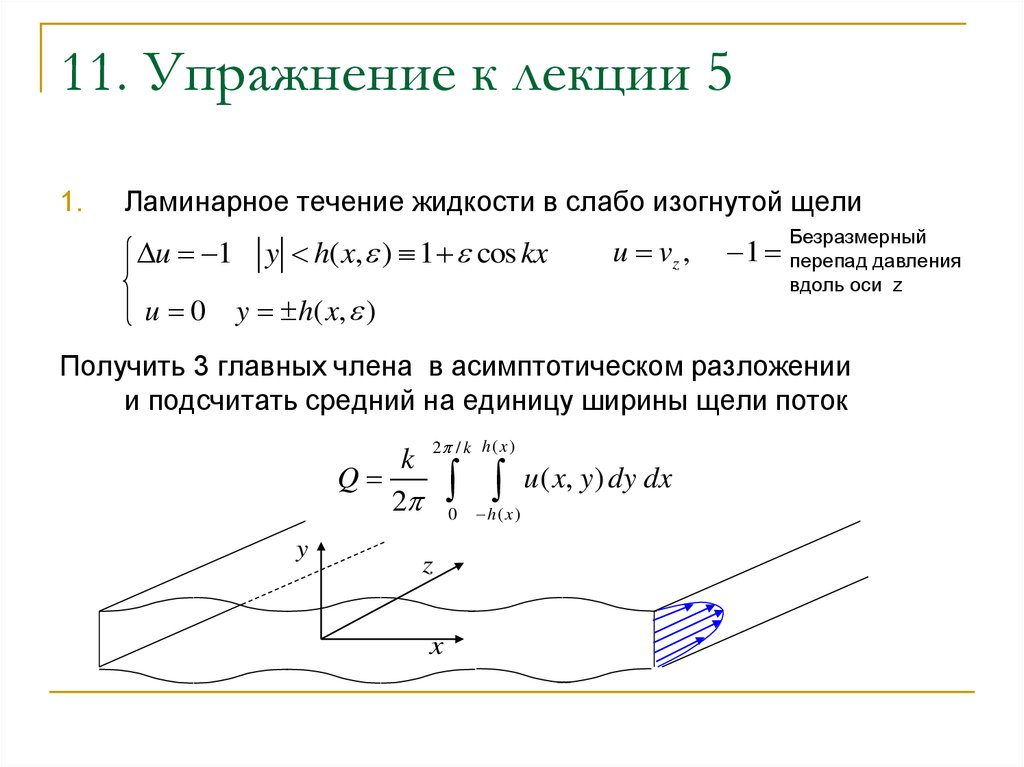
12. 11. Упражнение к лекции 5

1.
Ламинарное течение жидкости в слабо изогнутой щели
u 1
u 0
y h( x, ) 1 cos kx
u vz ,
y h( x, )
1
Безразмерный
перепад давления
вдоль оси z
Получить 3 главных члена в асимптотическом разложении
и подсчитать средний на единицу ширины щели поток
k
Q
2
y
2 / k h ( x )
0
z
x
h( x)
u ( x, y ) dy dx