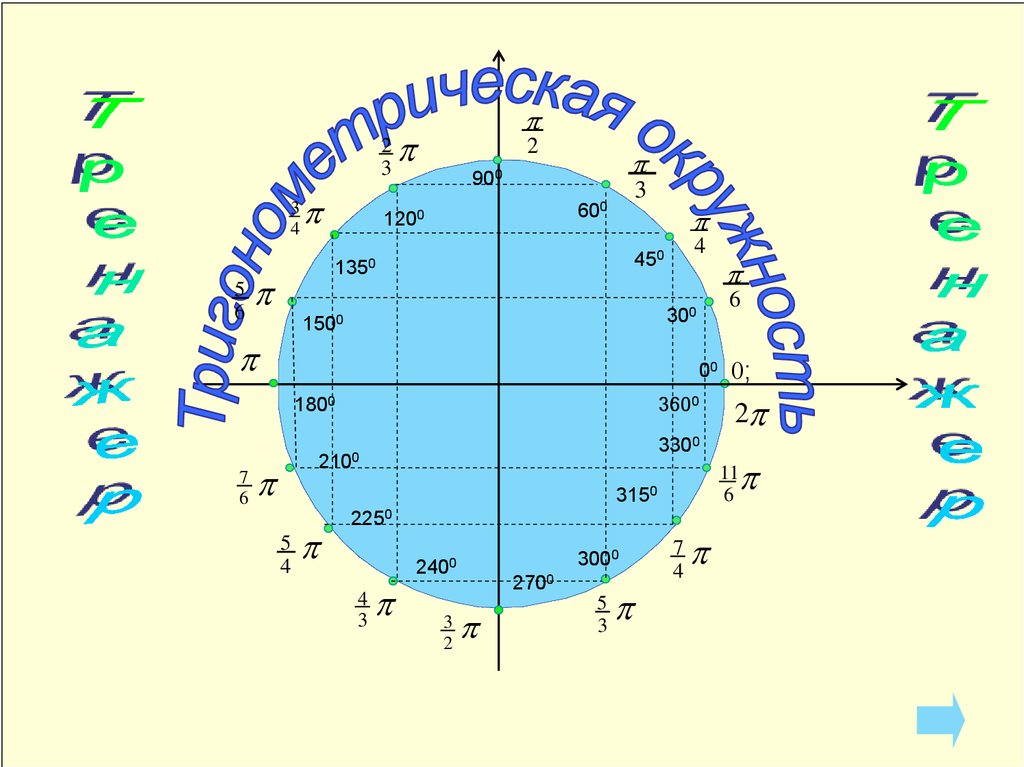
Единичная окружность

1.

2
3
3
4
5
6
p
p
p
2
p
900
3
600
1200
00
3600
1800
7
6
p
2250
3000
2400
4
3
2p
11
6
3150
5
4
0;
3300
2100
p
p
6
300
1500
p
4
450
1350
p
p
p
3
2
2700
p
5
3
p
7
4
p
p

2.

3.

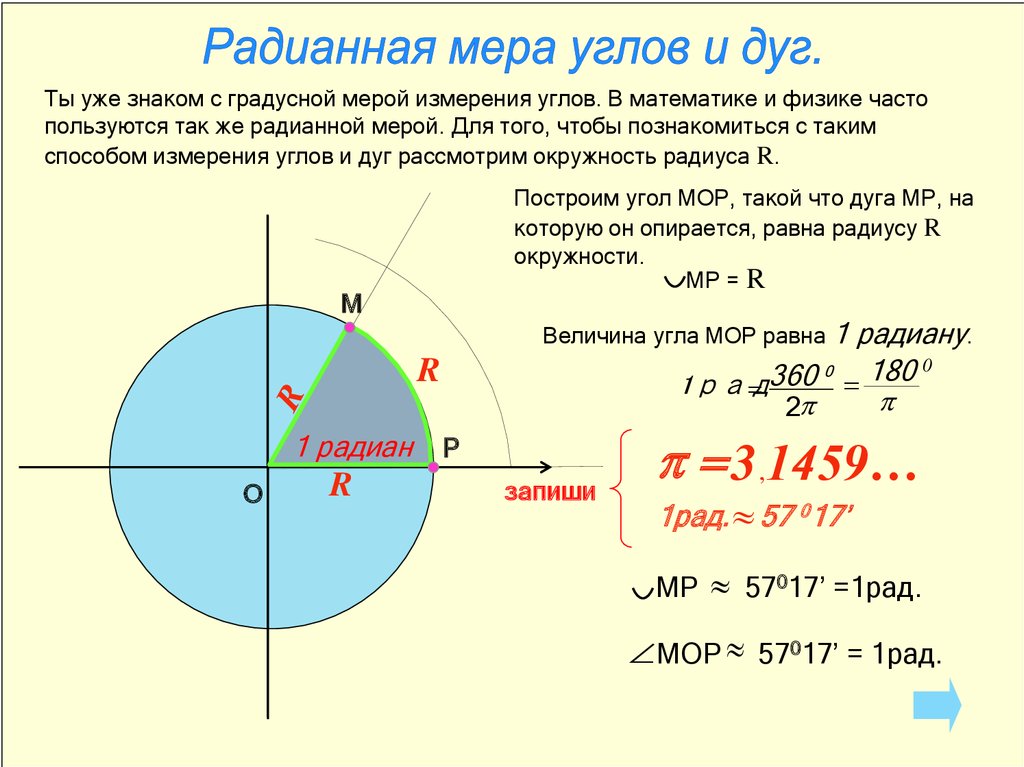
Ты уже знаком с градусной мерой измерения углов. В математике и физике часто
пользуются так же радианной мерой. Для того, чтобы познакомиться с таким
способом измерения углов и дуг рассмотрим окружность радиуса R.
Построим угол МОР, такой что дуга МР, на
которую он опирается, равна радиусу R
окружности.
МР = R
М
Величина угла МОР равна 1
радиану.
0
0
180
360
=
1рад
=
p
p
2
R
1 радиан
О
R
Р
запиши
p = 3,1459…
1рад. 57 017’
МР
57017’ =1рад.
МОР 57017’ = 1рад.

4.

Окружность, радиус которой равен 1, называется единичной.
p = 3,1459…
Y
М
Построим две взаимно перпендикулярных оси:
ось абсцисс и ось ординат.
Ты помнишь, что длина окружности
выражается формулой :
p
p
2
А
N
p
3
l = 2 p R,
где R – радиус окружности.
p
Длину единичной окружности удобно
измерять в радианах, т.к.
В 4
p
С 6
Р
2p
если R=1, то:
X
p
(рад.)
Тогда длина дуги половины окружности
равна:
p (рад.)
p
К 3
2
l = 2p
(рад.) - четверть длины окружности,
2
3p (рад.) - три четверти длины окружности.
2
Наименование радиан обычно опускают.
Точки М,Р,К,N – назовем узловыми.
Отметим так же точки: А,В,С.

5.

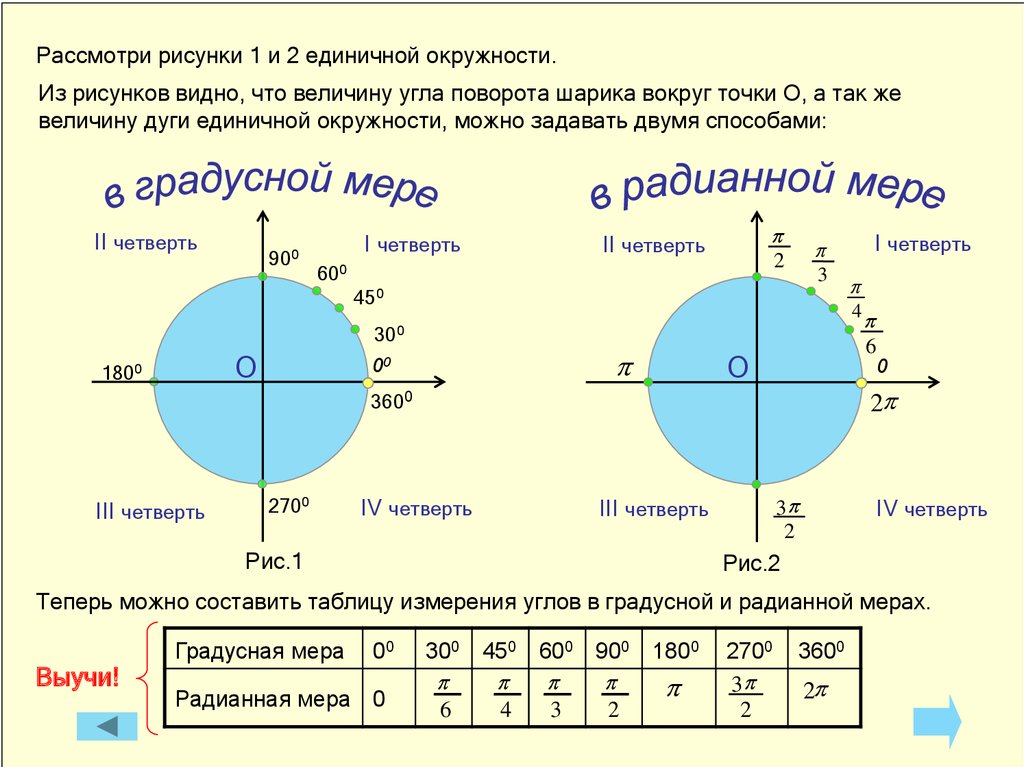
Рассмотри рисунки 1 и 2 единичной окружности.
Из рисунков видно, что величину угла поворота шарика вокруг точки О, а так же
величину дуги единичной окружности, можно задавать двумя способами:
II четверть
900
I четверть
p
II четверть
600
3
450
О
p
00
2700
IV четверть
О
0
2p
3p
2
III четверть
Рис.1
p
6
3600
III четверть
p
4
300
1800
I четверть
p
2
IV четверть
Рис.2
Теперь можно составить таблицу измерения углов в градусной и радианной мерах.
Выучи!
Градусная мера
00
Радианная мера 0
300 450
600
900 1800
p
p
p
p
6
4
3
2
p
2700
3p
2
3600
2p

6.

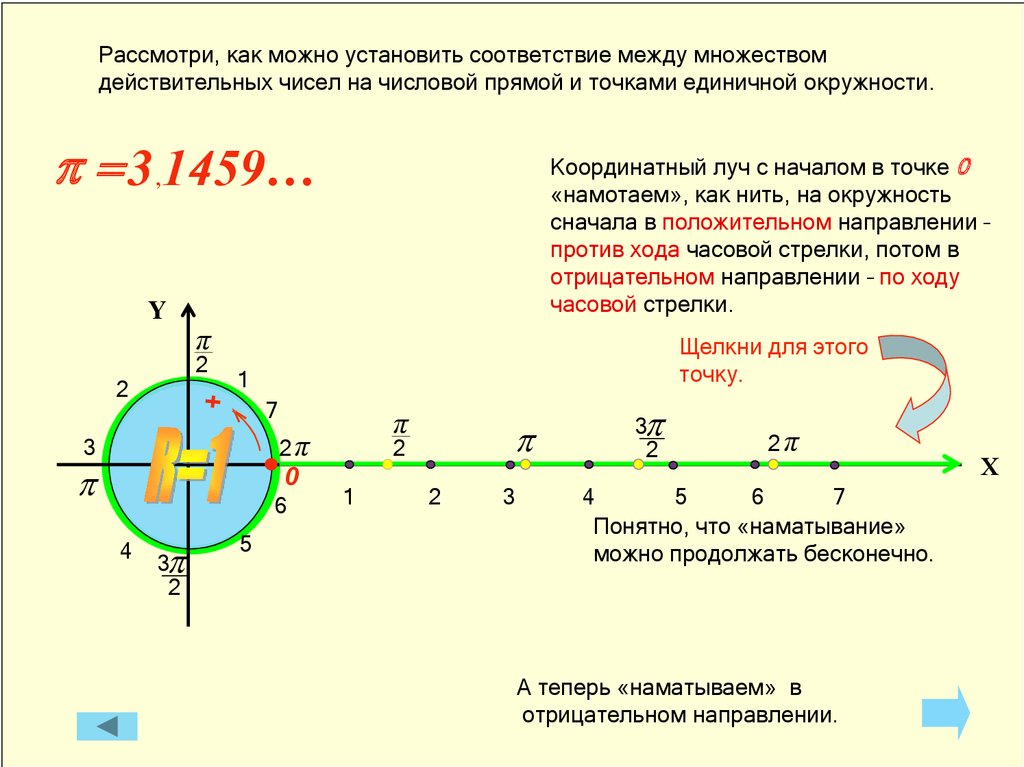
Рассмотри, как можно установить соответствие между множеством
действительных чисел на числовой прямой и точками единичной окружности.
p = 3,1459…
Y
π
2
2
Координатный луч с началом в точке 0
«намотаем», как нить, на окружность
сначала в положительном направлении –
против хода часовой стрелки, потом в
отрицательном направлении – по ходу
часовой стрелки.
Щелкни для этого
точку.
1
7
π
2π
3
p
0
6
4
3p
2
5
p
2
1
2
3
3p
2
2π
4
5
6
7
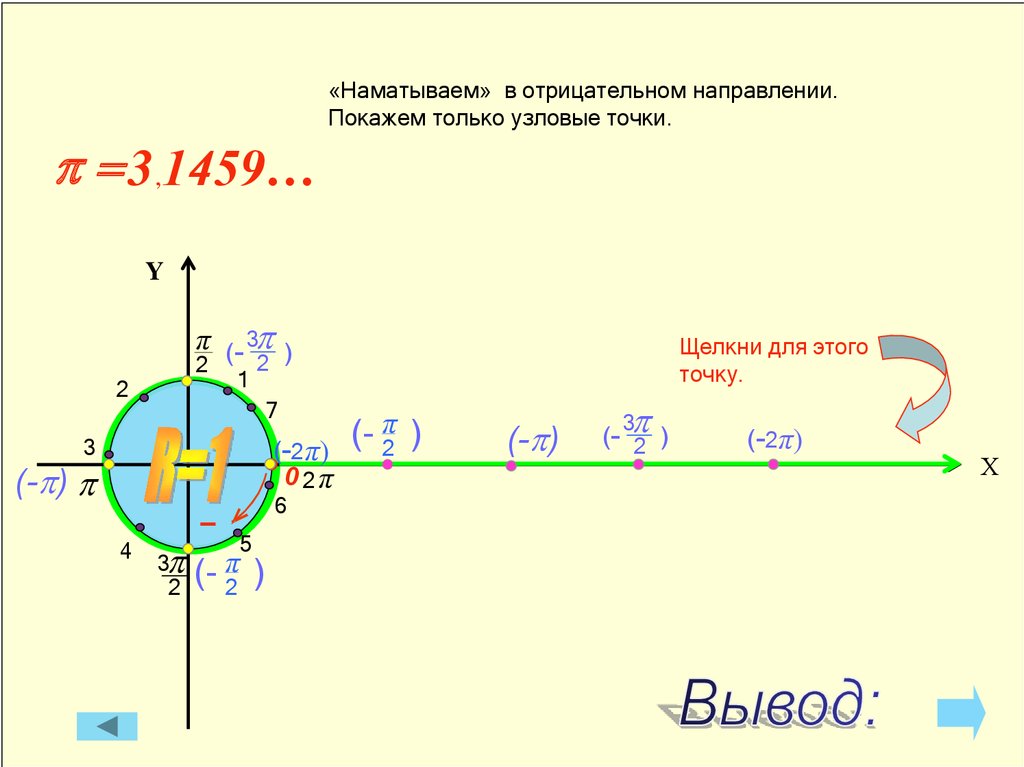
Понятно, что «наматывание»
можно продолжать бесконечно.
А теперь «наматываем» в
отрицательном направлении.
Х

7.

p = 3,1459…
«Наматываем» в отрицательном направлении.
Покажем только узловые точки.
Y
π (- 3p )
2
2
1
2
7
π )
(2
(-2π)
3
(-p) p
0 2π
6
4
Щелкни для этого
точку.
3p
2
5
(- π2 )
(-p)
3p
(- 2 )
(-2π)
Х

8.

•При рассмотрении единичной окружности удобно
использовать радианную меру, т.к. при этом числа,
выражающие длину дуги и длину окружности
кратные числа.
•Каждой точке окружности соответствует не одно, а
бесконечное множество действительных чисел.
•Каждому числу на окружности соответствует одна
(единственная) точка.
Например, точке М,
p + 2p = 5p
кроме числа p ,
2
2
( - 112p ) ( 92p )
( - 72p ) ( 52p )
(- 32p ) p2
900 М
(-p) p
p
3
p
600
4
0
45
300
2
соответствуют числа :
p
6
00 0
1800
N
Р
2 p (-2π)
p + 4p = 9p
2
2
p -2p =- 3p
2
2
p - 4p = - 7p
2
2
p - 6p = -11p
2
2700 К
(- π2 ) 32 p
Задание выполни письменно!
-Назови, кроме отмеченных, еще по одному
положительному и отрицательному числу,
которые соответствуют выделенным точкам
окружности.
2

9.

Будем рассматривать все точки единичной окружности как точки, полученные
поворотом точки Р0 вокруг начала координат на некоторый угол.
a0 =
600
(Р0
Щелкни по точке Рt
Рt).
Рt
Проследи, как будет меняться угол поворота
для точки Рt :
600 (4200) (-3000)
(7800) (-6600)
(11400) (-10200)
a
1 поворот: 600 -+360
36000==-420
30000
.36000=
2 поворот: 600 -+22.360
66000
=-780
.36000=
=-1020
114000
3 поворот: 600 -+33.360
* * * * * * * * * * * * * * *
Р0
.36000
k поворот: 600 -+kk.360
Вращаться можно как в положительном,
так и в отрицательном направлениях.
Для точки Рt все углы поворота
можно записать так:
запиши
a = a + 360 k
a = a + 2p k
0
0
0
1, 2 , 3 ...
,где k = 1, 2 , 3 ...
,где k =

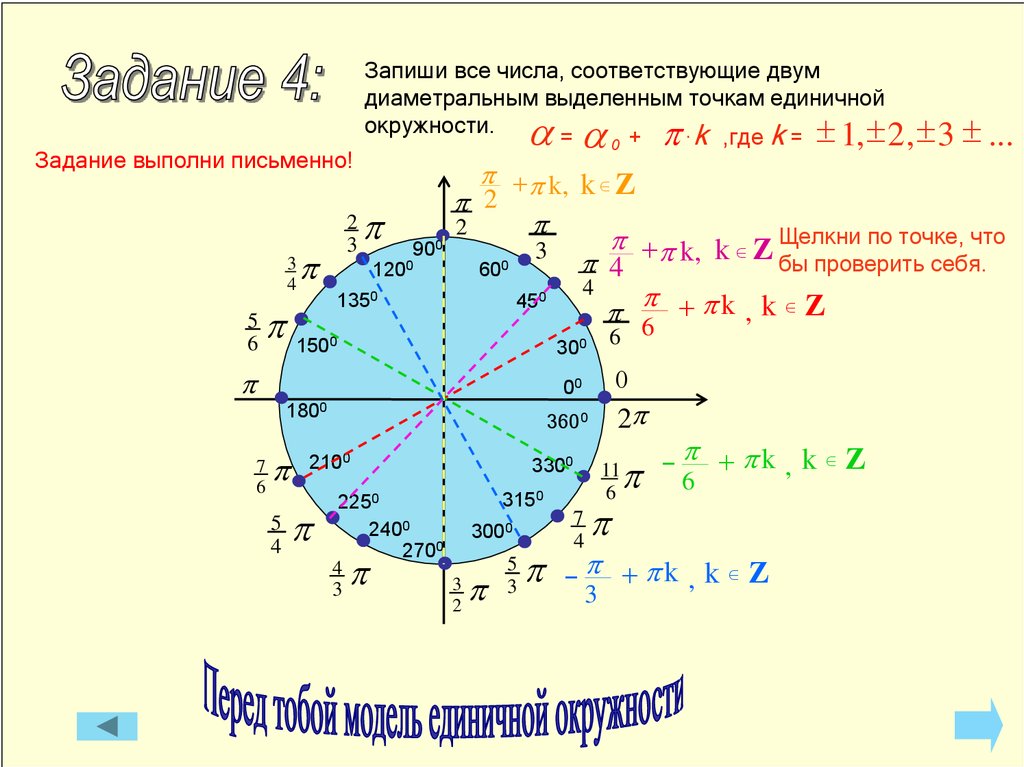
10.

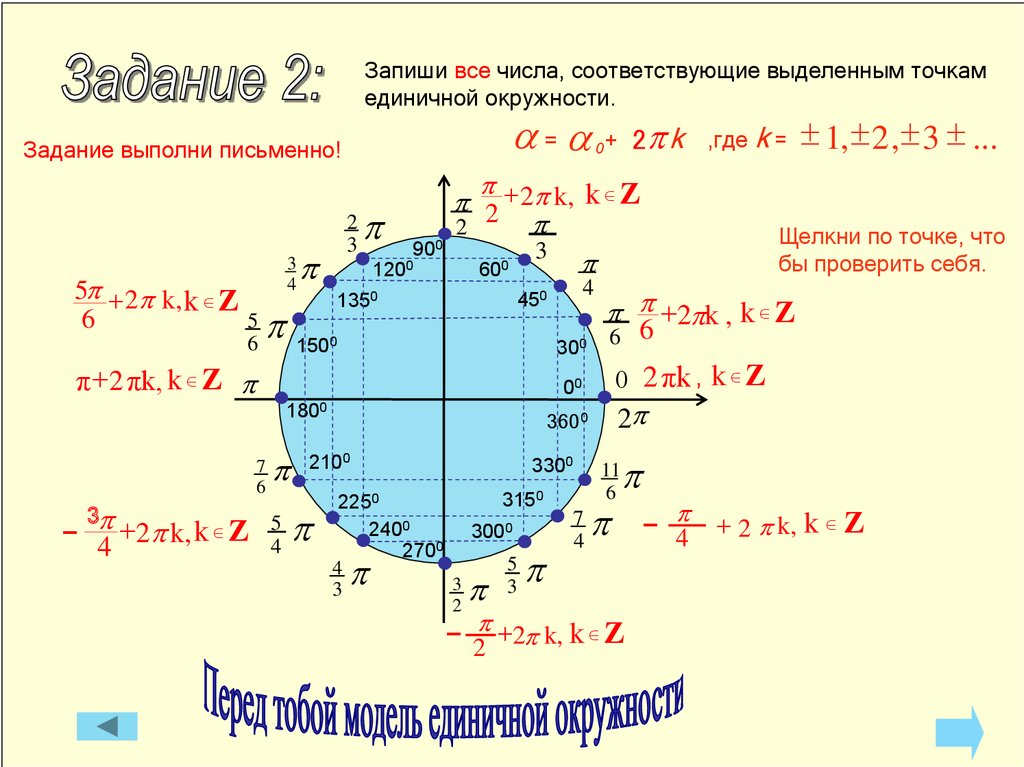
Запиши все числа, соответствующие выделенным точкам
единичной окружности.
a= a
Задание выполни письменно!
5p + 2p k, k Ζ
6
3
4
5
6
p
2
3
p
p
900
1200
3
600
300
00
1800
3p
- 4
+ 2p k, k Ζ
4
5
4
3600
2100
p
3300
3150
2250
4
3
p
2400
2700
3000
3
2
p
5
3
p
p p +2pk , k Ζ
6
6
0 2 πk , k Ζ
2p
11
6
7
4
1, 2 , 3 ...
Щелкни по точке, что
бы проверить себя.
p
450
1350
1500
p
,где k =
p
p 2 + 2p k, k Ζ
p
2
π+ 2 πk, k Ζ p
7
6
2p k
0+
p
p -
- 2p + 2p k, k Ζ
p + p k, k Ζ
2
4

11.

3
4
5
6
p
2
3
p
p
p
p
2
900
1200
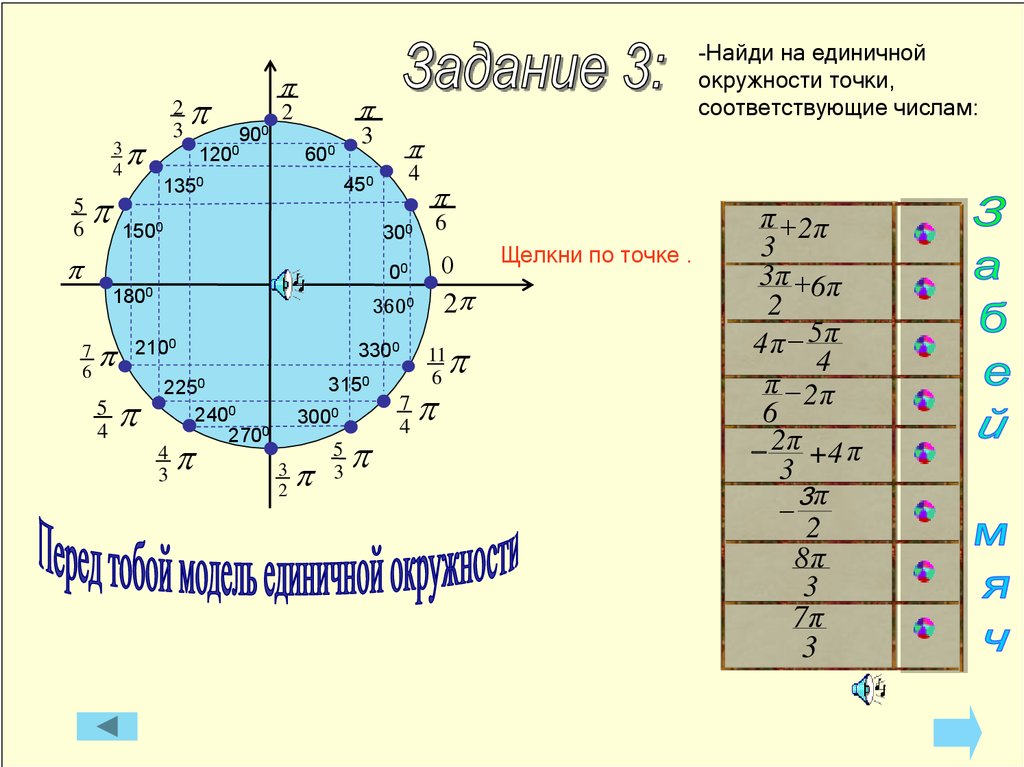
-Найди на единичной
окружности точки,
соответствующие числам:
3
600
p
4
450
1350
1500
300
p
p
6
0
00
1800
7
6
p
5
4
2100
p
2p
3600
3300
3150
2250
4
3
p
2400
2700
3000
3
2
p
5
3
p
11
6
7
4
p
p
Щелкни по точке .
π + 2π
3
3π +6π
2
4π - 5π
4
π - 2π
6
- 2π +4 π
3
π
-3
2
8π
3
7π
3

12.

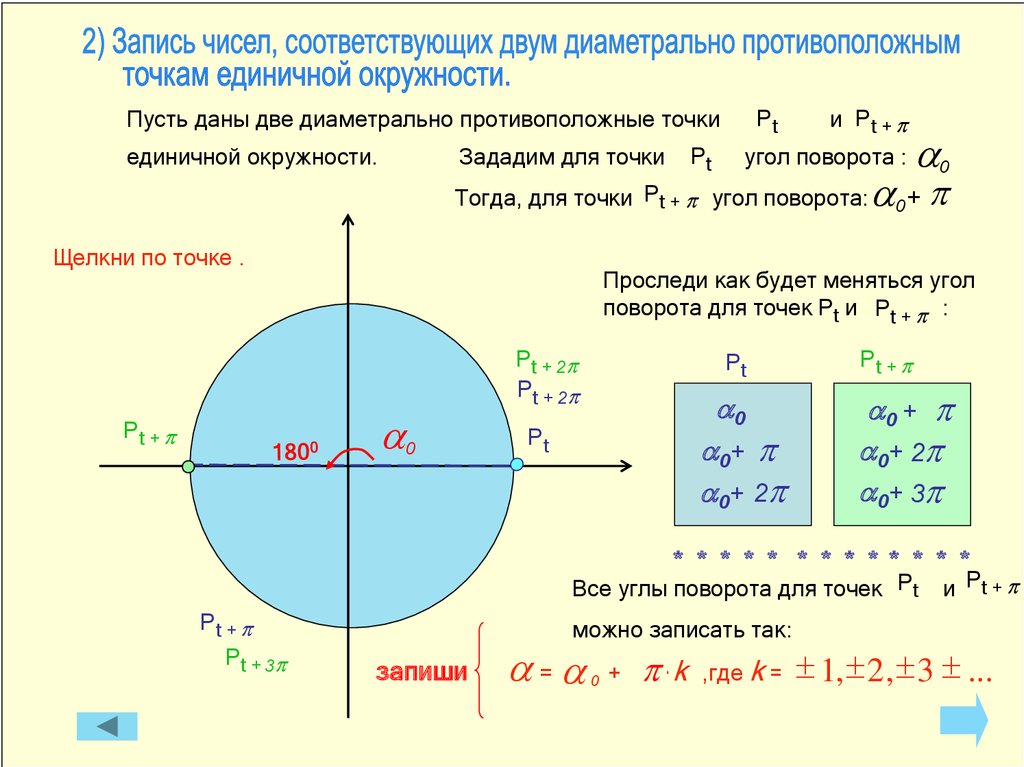
Пусть даны две диаметрально противоположные точки
единичной окружности.
Рt
Зададим для точки
Рt
и Рt + p
угол поворота :
Тогда, для точки Рt + p угол поворота:
Щелкни по точке .
a0+ p
Проследи как будет меняться угол
поворота для точек Рt и Рt + p :
a0
Рt + p
a0
Рt + 2 p
Рt + 2 p
Рt
a0
a 0+ p
a0+ 2p
Рt
Рt + p
a0 + p
a0+ 2p
a0+ 3p
* * * * * * * * * * * * *
Все углы поворота для точек Рt
Рt + p
Рt + 3p
и Рt + p
можно записать так:
запиши
a= a
0
+
pk
,где k =
1, 2 , 3 ...

13.

Задание выполни письменно!
3
4
5
6
p
2
3
p
Запиши все числа, соответствующие двум
диаметральным выделенным точкам единичной
окружности.
=
+
k ,где k =
a a
p
p
p +p k, k Ζ
2
p
2
900
1200
600
1350
p +p k, k Ζ Щелкни по точке, что
бы проверить себя.
p 4
4
p
p 6 + pk , k Ζ
3
450
1500
6
300
p
0
00
1800
7
6
p
5
4
2p
3600
2100
p
3300
3150
2250
4
3
p
2400
2700
3000
3
2
1, 2 , 3 ...
p
0
p
5
3
p
11
6
7
4
p
-p + pk , k Ζ
6
p
-p + pk , k Ζ
3

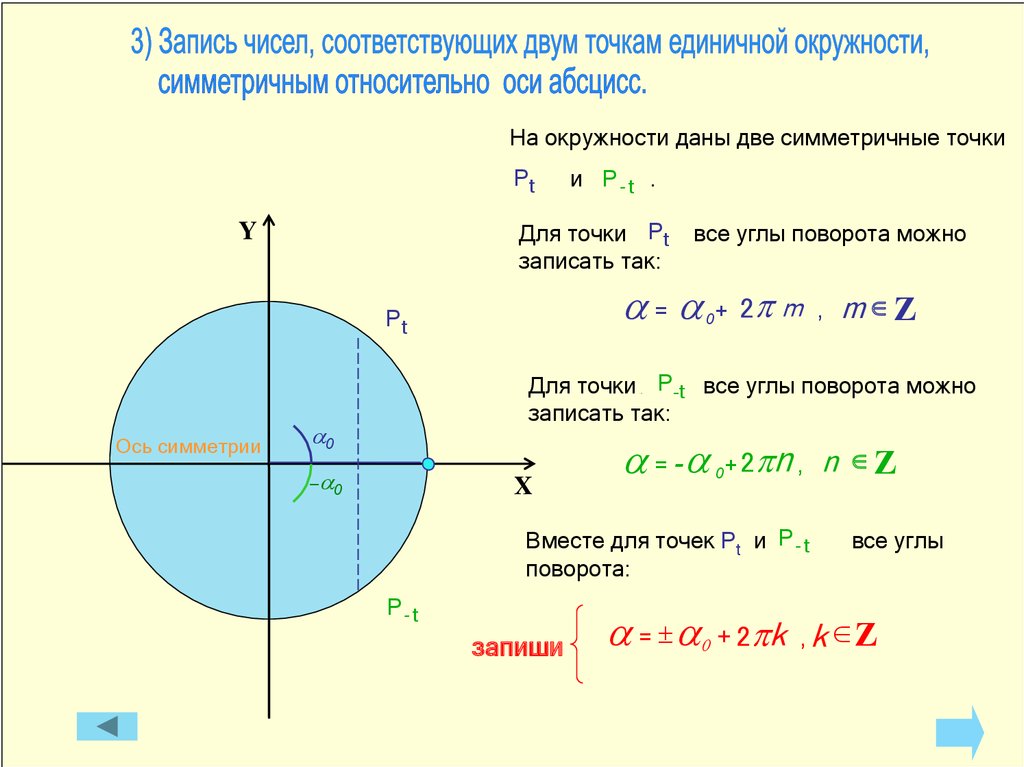
14.

На окружности даны две симметричные точки
Рt
Для точки Рt
записать так:
Y
0
,
m Ζ
Для точки Р-t все углы поворота можно
записать так:
a0
_a
все углы поворота можно
a = a + 2p m
Рt
Ось симметрии
и Р- t .
X
0
a = -a
0+
2pn , n Ζ
Вместе для точек Рt и Р- t
поворота:
Р- t
запиши
все углы
a = a0 + 2pk , k Ζ

15.

На окружности даны две симметричные точки
Рt
Для точки Рt
записать так:
Y
0
,
m Ζ
Для точки Р-t все углы поворота можно
записать так:
p - a0
a0
Ось симметрии
все углы поворота можно
a = a + 2p m
Рt
Рp - t
p
и Рp - t .
X
a = p -a
0+
2pn , n Ζ
Вместе для точек Рt и Рp - t все углы поворота:
запиши
a = (-1)ka0 + pk , k Ζ

16.

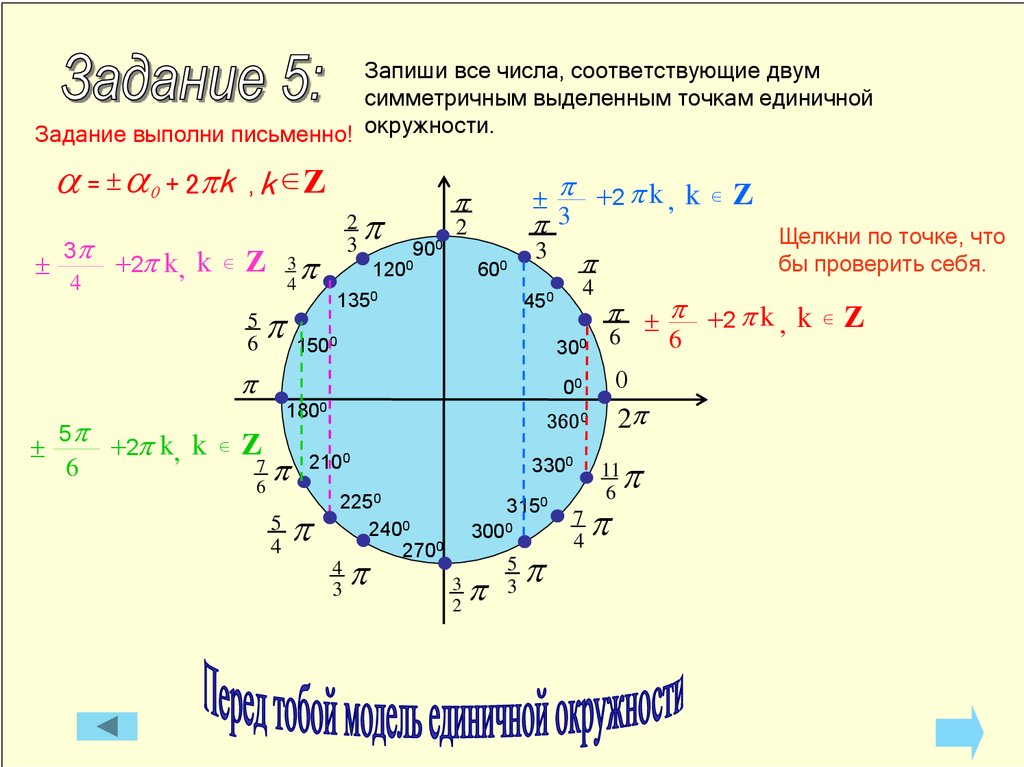
Запиши все числа, соответствующие двум
симметричным выделенным точкам единичной
Задание выполни письменно! окружности.
a = a0 + 2pk , k Ζ
3p
4
+2p k, k
Ζ
5
6
3
4
p
2
3
p
p
p +2 p k , k
p3
p
2
900
1200
600
1350
3
1500
300
6
Ζ
7
6
p
6
0
5
4
p
2p
3600
2100
3300
2250
4
3
p
3150
2400
2700
3000
3
2
p
5
3
p
11
6
7
4
Ζ
Щелкни по точке, что
бы проверить себя.
p p +2 p k , k
6
00
1800
+2p k, k
4
450
p
5p
p
p
p
Ζ

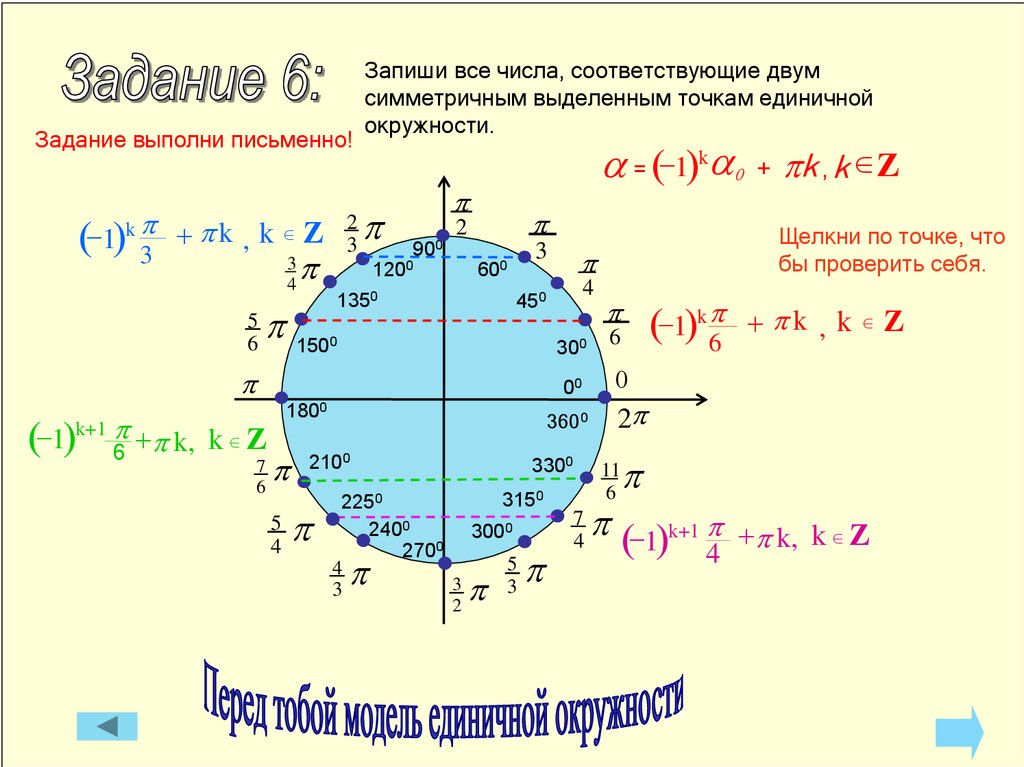
17.

Задание выполни письменно!
(-1)k p3
+ pk , k Ζ
3
4
5
6
p
2
3
p
Запиши все числа, соответствующие двум
симметричным выделенным точкам единичной
окружности.
p
a = (-1)ka0 + pk , k Ζ
p
p
2
900
1200
3
600
1350
(-1)
4
300
p
k+1
p
450
1500
00
p +p k, k Ζ
6
7
6
1800
p
5
4
3600
2100
p
3300
3150
2250
4
3
p
2400
2700
3000
3
2
p
5
3
p
Щелкни по точке, что
бы проверить себя.
p
6
+ pk , k
0
2p
11
6
7
4
(-1)k p6
p
p (-1)k+1 p +p k,
4
k Ζ
Ζ

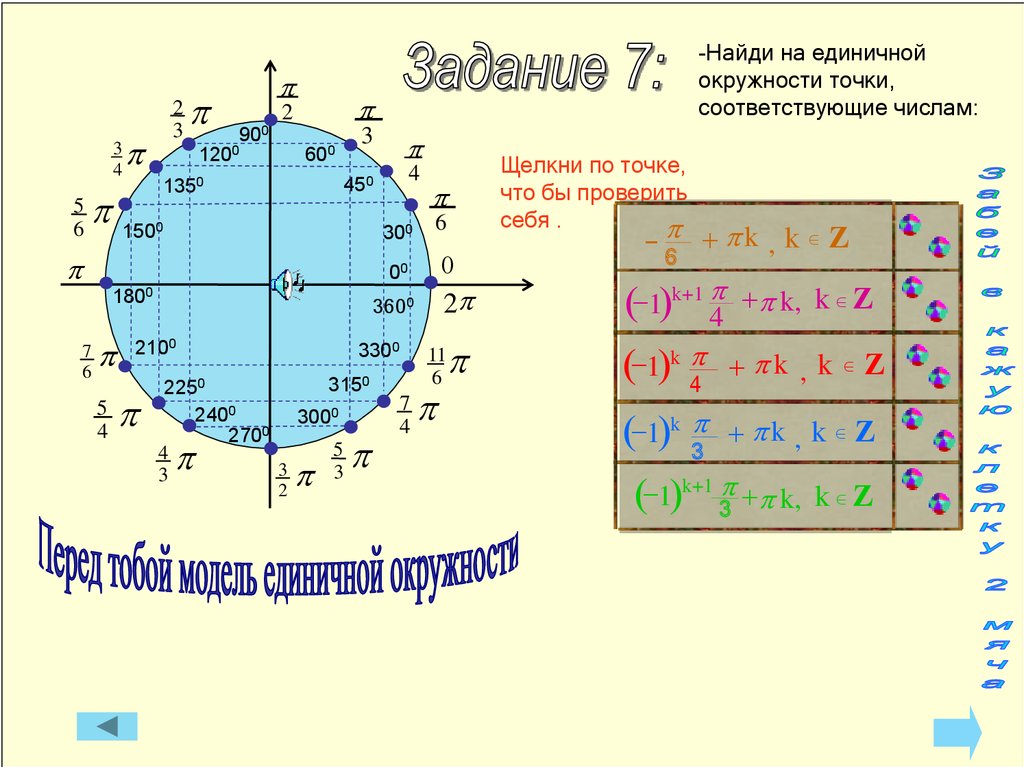
18.

3
4
5
6
p
2
3
p
p
p
p
2
900
1200
-Найди на единичной
окружности точки,
соответствующие числам:
3
600
p
4
450
1350
1500
300
p
p
6
0
00
1800
7
6
p
5
4
3600
2100
p
3300
3150
2250
4
3
p
2400
2700
3000
3
2
p
5
3
p
p
-6 + pk , k Ζ
2p
(-1)k+1 p4
p
(-1)k p4
+ pk , k
(-1)k p3
+ pk , k Ζ
11
6
7
4
Щелкни по точке,
что бы проверить
себя .
p
+p k, k Ζ
(-1)k+1 p3 +p k,
Ζ
k Ζ

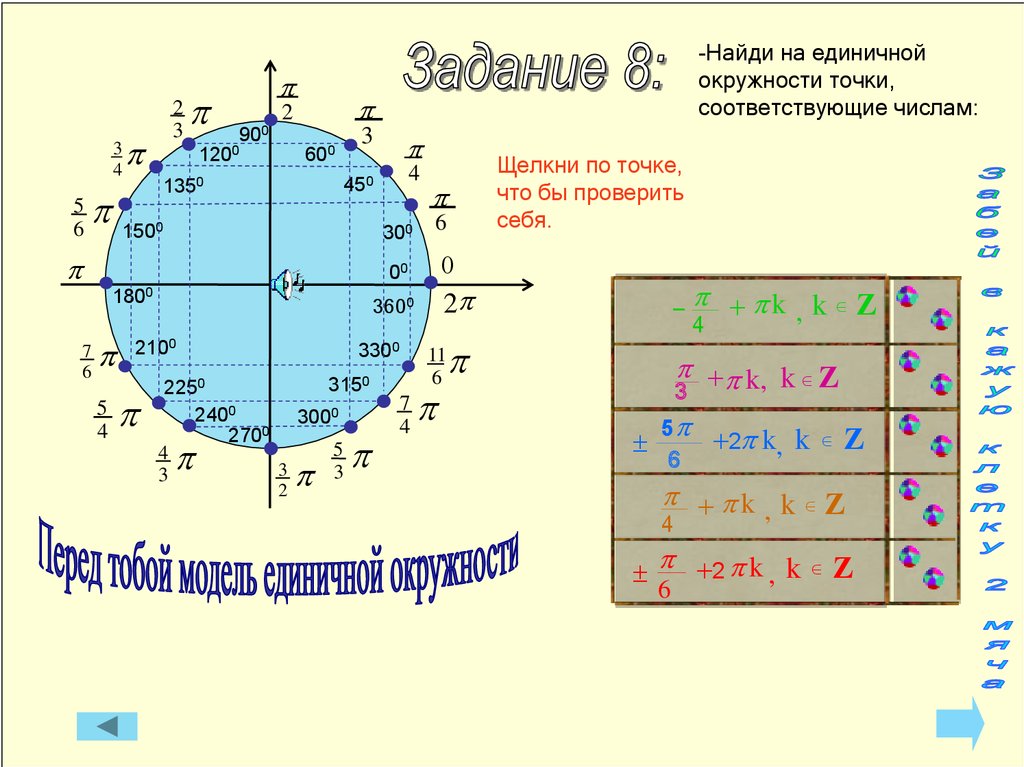
19.

3
4
5
6
p
2
3
p
p
p
p
2
900
1200
-Найди на единичной
окружности точки,
соответствующие числам:
3
600
p
4
450
1350
1500
300
p
p
6
0
00
1800
7
6
p
5
4
p
3300
3150
2250
4
3
p
2400
2700
3000
3
2
p
5
3
p
11
6
7
4
+ pk , k Ζ
-p
4
2p
3600
2100
Щелкни по точке,
что бы проверить
себя.
p
p
p +p k, k Ζ
3
5p
6
+2p k, k
Ζ
p + pk , k Ζ
4
p +2 p k , k
6
Ζ