Похожие презентации:
Прямоугольный треугольник
1. Прямоугольный треугольник
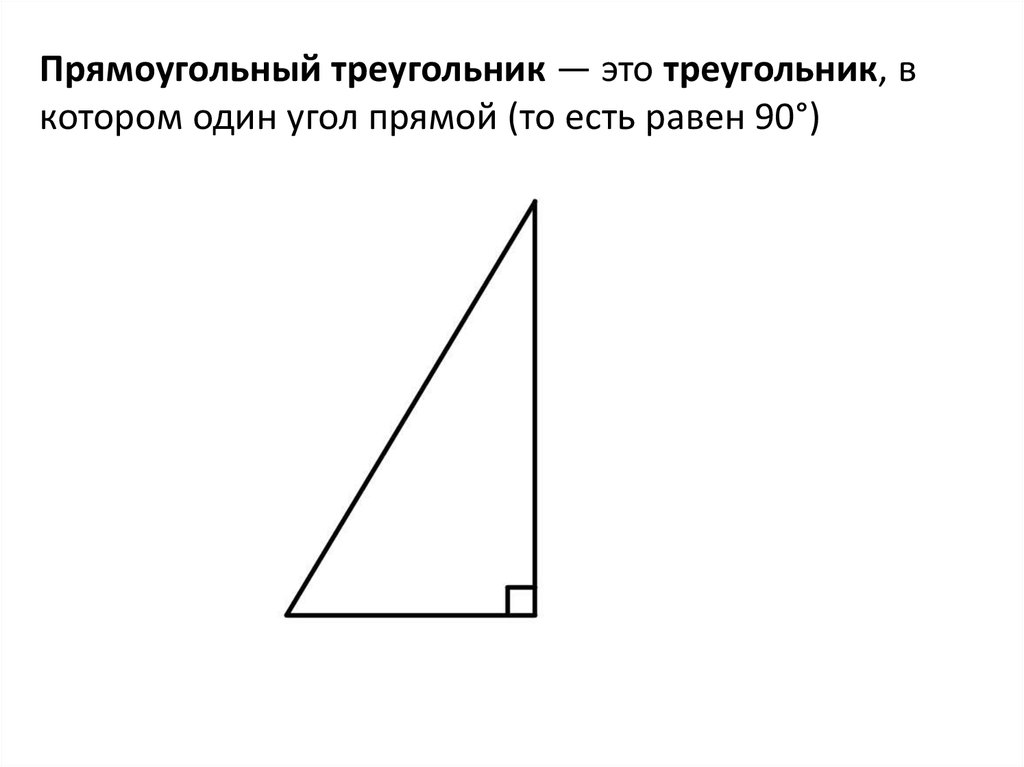
2. Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть равен 90°)
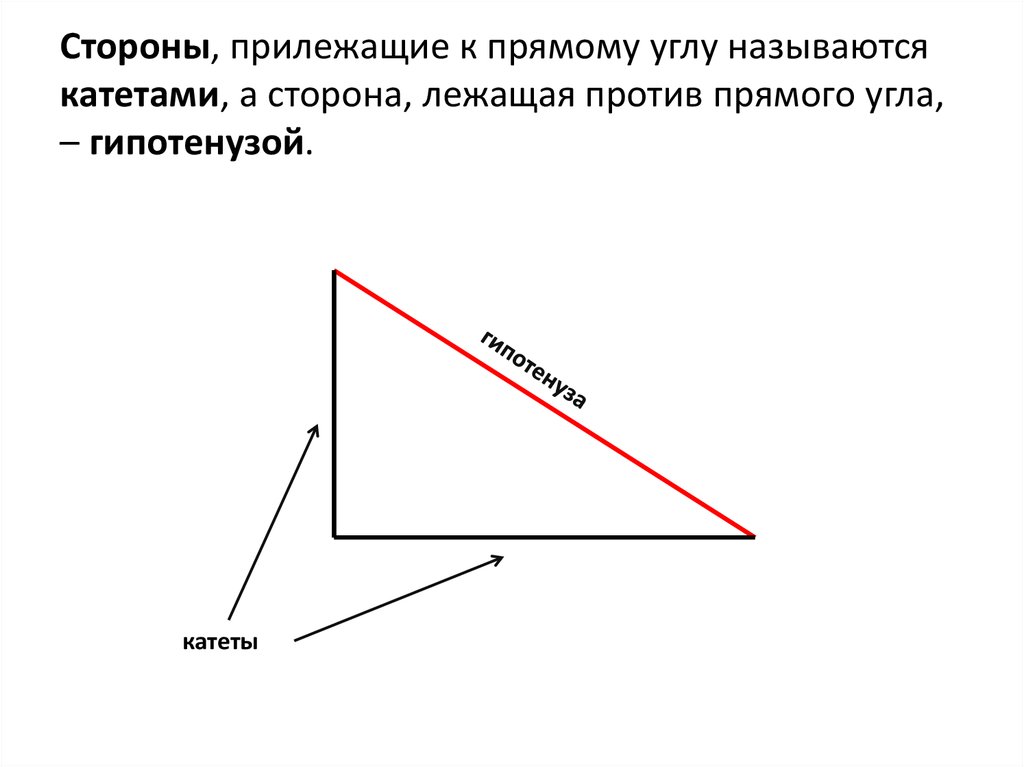
3. Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой.
катеты4. Свойства
Сумма острых углов прямоугольноготреугольника 90°
Две высоты прямоугольного треугольника
совпадают с его катетами
А
BAC+BCA=90°
С
B
5.
Катет, лежащий против угла в 30°, равенполовине гипотенузы
А
B
BAC=30°
AB=0,5 AC
С
6.
Медиана прямоугольного треугольника,проведенная из вершины прямого угла на
гипотенузу, является радиусом описанной около
этого треугольника окружности:
7.
Теорема ПифагораВ прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
AC2+AB2=BC2
B
А
С
8.
Площадь прямоугольного треугольника равнаполовине произведения катетов и
вычисляется по формуле
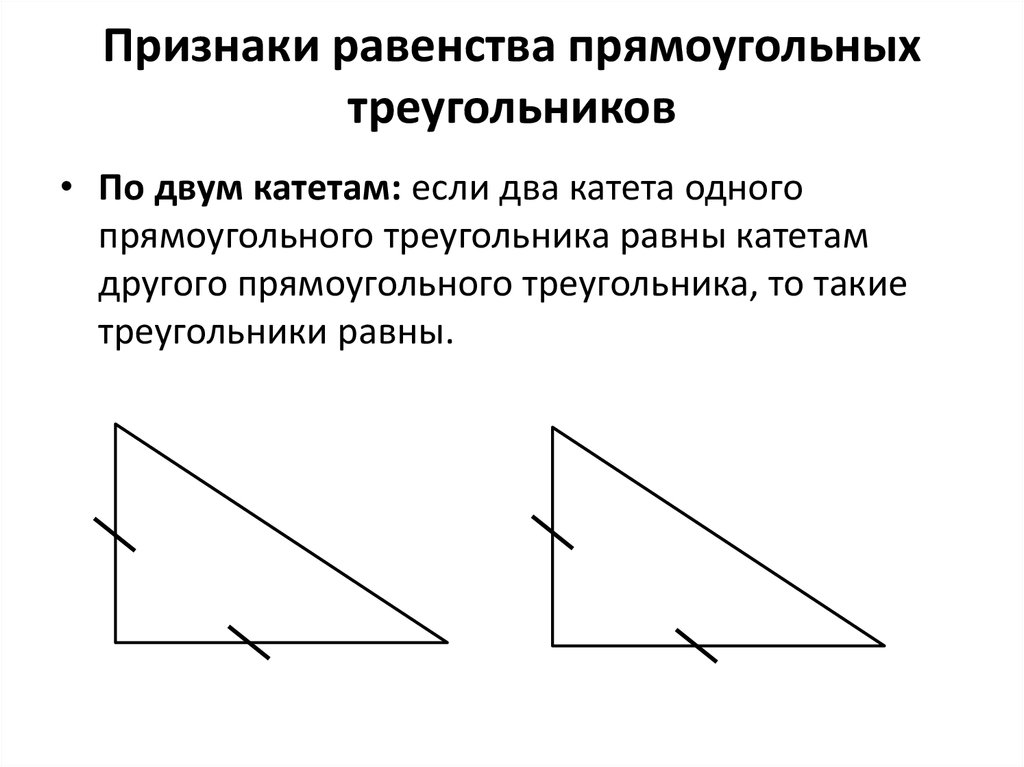
9. Признаки равенства прямоугольных треугольников
• По двум катетам: если два катета одногопрямоугольного треугольника равны катетам
другого прямоугольного треугольника, то такие
треугольники равны.
10.
• По гипотенузе и катету: если гипотенуза и катетодного прямоугольного треугольника
соответственно равны гипотенузе и катету другого
прямоугольного треугольника, то такие
треугольники равны.
11.
• По стороне и острому углу: Если сторона иприлежащий к ней острый угол одного
прямоугольного треугольника соответственно
равны стороне и прилежащему к ней острому углу
другого прямоугольного треугольника, то такие
треугольники равны







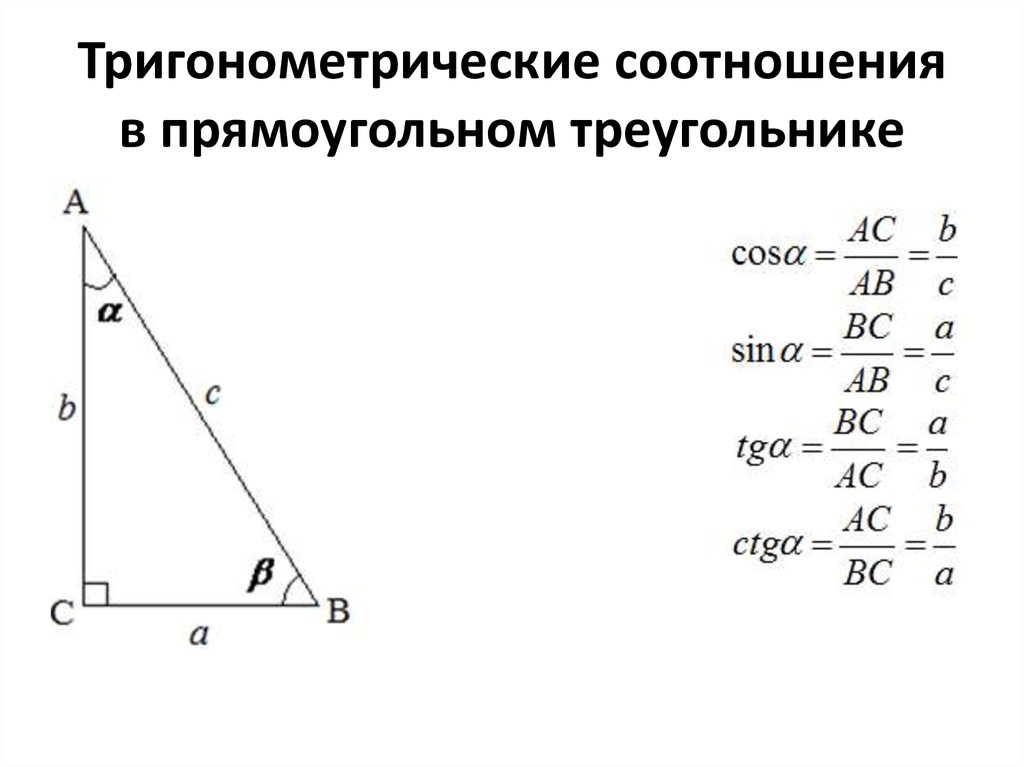
 Математика
Математика








