Прямоугольный треугольник. Стороны прямоугольного треугольника

1.

КЛАСС
Прямоугольный
треугольник

2.

катет
А
С
катет
В

3. Назови стороны прямоугольного треугольника

АС - катет
АВ -гипотенуза
В
ВС
-
С
катет
А

4.

Реши задачу
В
А
С

5.

Признаки равенства прямоугольных
треугольников
Теорема: Если катеты одного
прямоугольного треугольника
соответственно равны катетам
другого треугольника, то такие
треугольники равны
Теорема: Если катет и
прилежащий к нему острый угол
одного прямоугольного
треугольника соответственно
равны катету и прилежащему к
нему острому углу другого, то
такие треугольники равны
K
А
L
K
M С
А
В
L
M С
В

6.

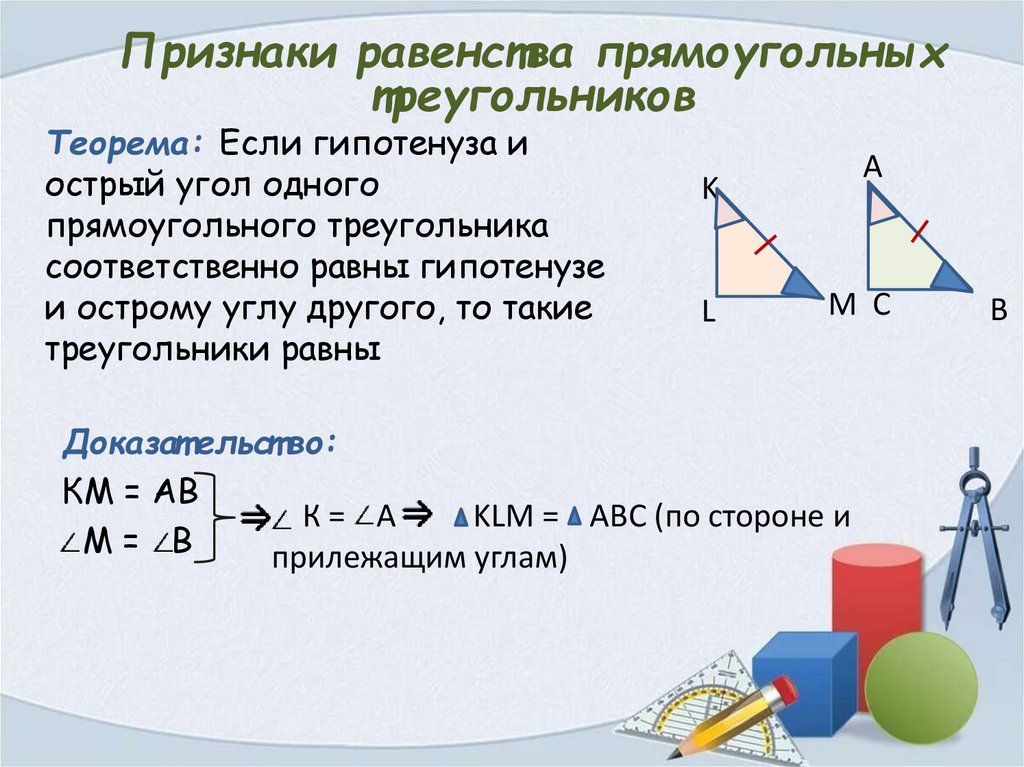
Признаки равенства прямоугольных
треугольников
Теорема: Если гипотенуза и
острый угол одного
прямоугольного треугольника
соответственно равны гипотенузе
и острому углу другого, то такие
треугольники равны
А
K
L
M С
Доказат ельст во:
КМ = АВ
К= А
KLM = ABC (по стороне и
М= В
прилежащим углам)
В

7.

Признаки равенства прямоугольных
треугольников
Теорема: Если гипотенуза и катет
одного прямоугольного
треугольника соответственно
равны гипотенузе и катету другого
треугольника, то такие
треугольники равны.
K
L
А
M С
Доказат ельст во:
L= C
KM = AB
можно наложить один треугольник на другой
LM = CB
Вершина K совместится с вершиной A, тогда и
вершины М и В тоже совместятся
А
С
В
В2
В

8.

Определите признак равенства
треугольников
1 вариант
1
2
3
2 вариант
1
2
3

9. Предполагаемые гипотезы

1. Сумма острых углов прямоугольного
треугольника равна 900.
2. Катет прямоугольного треугольника,
лежащий против угла в 300, равен
половине гипотенузы.
3. Если катет прямоугольного треугольника
равен половине гипотенузы, то угол,
лежащий против этого катета, равен 300.

10.

Свойство 1
Сумма двух острых углов
прямоугольного треугольника
равна 90°.
Доказательство:
Сумма углов треугольника равна 180° , а
прямой угол равен 90° , поэтому сумма двух
острых углов прямоугольного треугольника
равна 90° .

11.

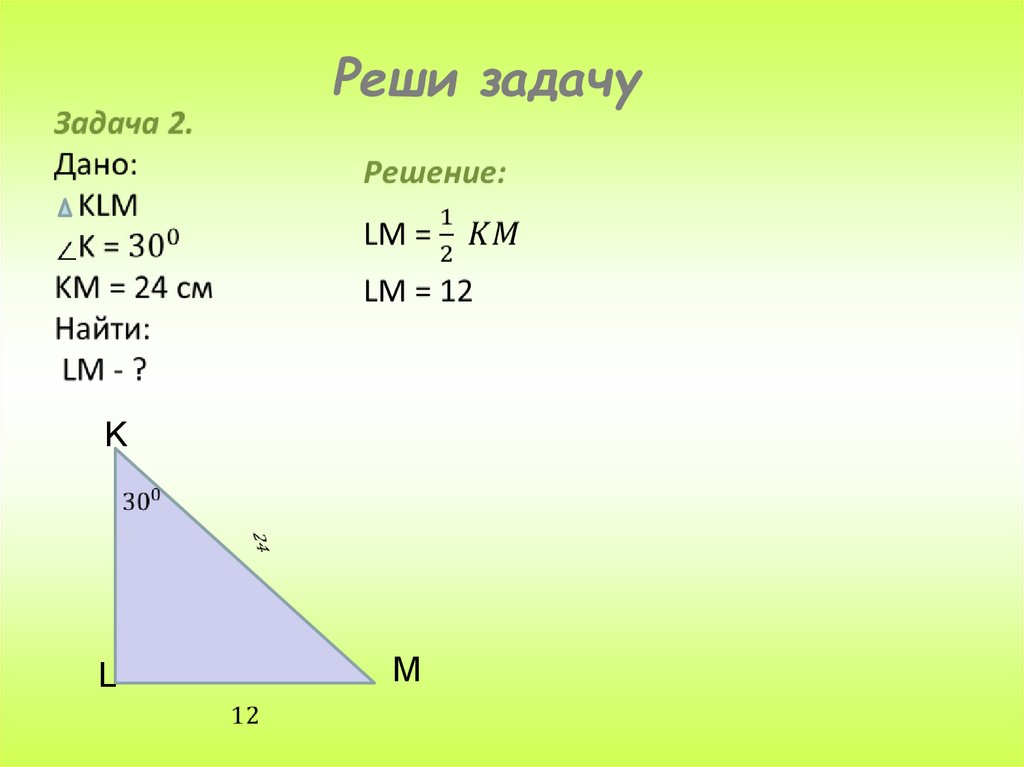
Реши задачу
K
L
M

12.

Свойство 2
Катет прямоугольного треугольника , лежащий
против угла в 30°, равен половине гипотенузы.
Рассмотрим прямоугольный треугольник,
В
в котором A -прямой, B =30° и значит, C=60°.
Докажем, что AC =1 2 BC.
Доказательство:
30° 30°
60°
D
Приложим к треугольнику АВС равный
ему треугольник АВD.
60°
С Получим треугольник ВСD, в котором
А
В= D=60°, поэтому DС=ВС. Но
АС=1 2 DС. Следовательно, AC =1 2
BC, что и требовалось доказать.

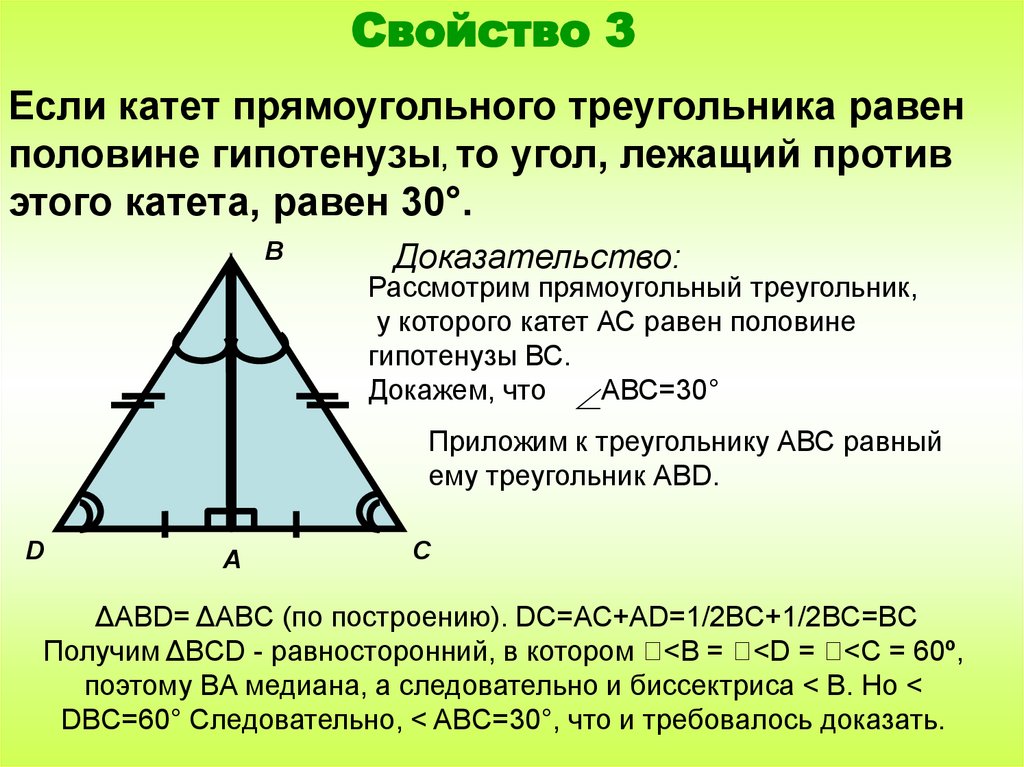
13.

Свойство 3
Если катет прямоугольного треугольника равен
половине гипотенузы, то угол, лежащий против
этого катета, равен 30°.
В
Доказательство:
Рассмотрим прямоугольный треугольник,
у которого катет АС равен половине
гипотенузы ВС.
Докажем, что АВС=30°
Приложим к треугольнику АВС равный
ему треугольник АВD.
D
А
С
ΔАВD= ΔАBС (по построению). DC=АС+AD=1/2BC+1/2BC=BC
Получим ΔBСD - равносторонний, в котором <B = <D = <С = 60º,
поэтому BA медиана, а следовательно и биссектриса < В. Но <
DBC=60° Следовательно, < AВC=30°, что и требовалось доказать.

14.

Решение задач
В
Найти: < В
37 0
С
А

15.

Найти: < САВ
В
70 0
А
D
С

16.

Найти: ВС
В
30°
А
С

17.

18.

19.

Контрольный тест
1. Прямоугольным называется треугольник, у которого
а) все углы прямые;
б) два угла прямые;
в) один прямой угол.

20.

Контрольный тест
2. В прямоугольном треугольнике всегда
а) два угла острых и один прямой;
б) один острый угол, один прямой и один тупой угол;
в) все углы прямые.

21.

Контрольный тест
3. Стороны прямоугольного треугольника, образующие
прямой угол, называются
а) сторонами треугольника;
б) катетами треугольника;
в) гипотенузами треугольника.

22.

Контрольный тест
4. Сторона прямоугольного треугольника,
противолежащая прямому углу, называется
а) стороной треугольника;
б) катетом треугольника;
в) гипотенузой треугольника.

23.

Контрольный тест
5. Сумма острых углов прямоугольного треугольника
равна
а) 180°;
б) 100°;
в) 90°.