Похожие презентации:
Синтез сополимеров с заданным порядком присоединения звеньев в цепи методом интербиполиконденсации
1.
СИНТЕЗ СОПОЛИМЕРОВ С ЗАДАННЫМПОРЯДКОМ ПРИСОЕДИНЕНИЯ ЗВЕНЬЕВ В
ЦЕПИ МЕТОДОМ
ИНТЕРБИПОЛИКОНДЕНСАЦИИ
Кузнецов Александр Алексеевич
ИСПМ им. Н.С.Ениколопова РАН
1
2.
План доклада• Характеристики микроструктуры цепи
сополимеров
• Упорядоченность звеньев в цепи. Блоксополимеры и структуры «голова-хвост»
• Расчет упорядоченности звеньев в цепях
поликонденсационных сополимеров для разных
реакционных схем исходя из кинетических
данных
2
3.
Tg2Что изменяется при переходе от гомополимера к
бинарному СПЛ:
при статистическом распределении звеньев : Tg1
Настройка основных характеристик ( Tg, Tm, и т.п.)
Новое свойство за счет введения новых звеньев
P1
(нелинейные оптические свойства);
при упорядоченном распределении звеньев (блок-СПЛ):
Группа новых свойств через самоорганизацию и
изменение фазовой морфологии;
при упорядоченном распределении звеньев (чередующийся
СПЛ):
Изменение релаксационных характеристик
3
4.
Микроструктура цепи бинарных линейных СПЛKM
Pab
Pab
Pab 2 Paa Pab 2 Pbb
где Paa, Pbb, Pab – мольные фракции диад “aa”“bb”,
”ab”
aaaabbbbbaaaabbbbb
Блок-сополимер 0<Кm<1
(Диблок-, триблок-, мультиблок-)
Тg1, Tg2, Tm1, Tm2
abaababbabaabbababa
Статистический сополимер Km=1
Тg1<Tg<Tg2,
ababababababababab
Чередующийся сополимер Km = 2 Тg1<Tg<Tg2 Tg
Градиентный полимер
4
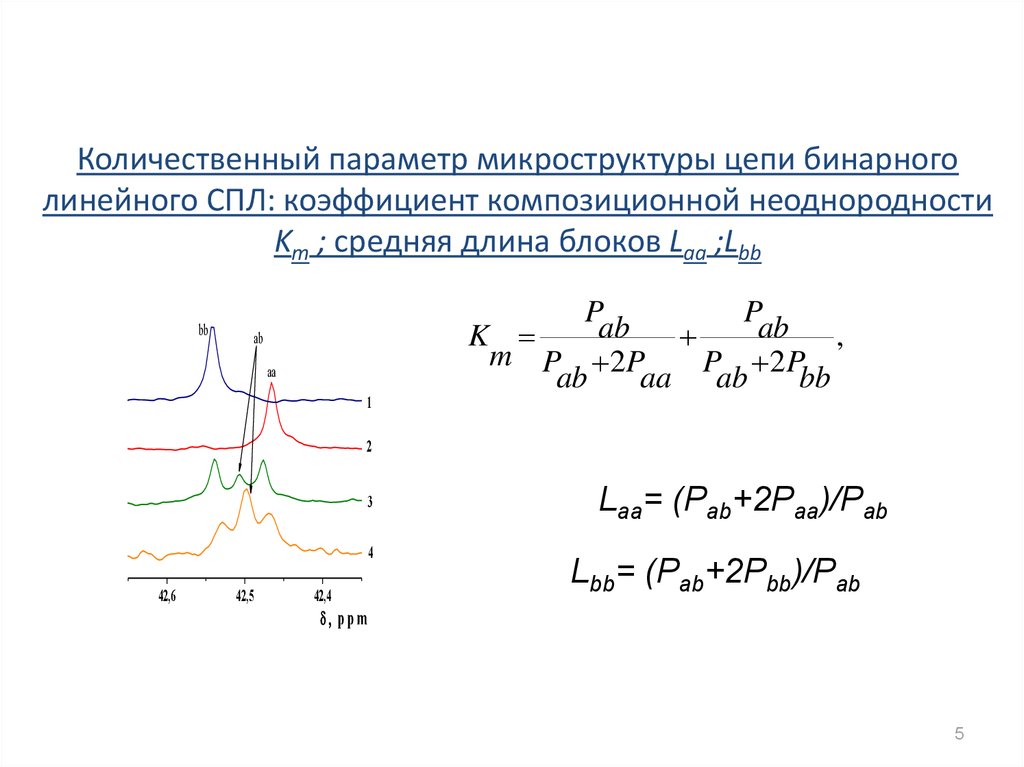
5. Количественный параметр микроструктуры цепи бинарного линейного СПЛ: коэффициент композиционной неоднородности Km ; средняя
длина блоков Laa ;Lbbbb
ab
aa
1
P
P
ab
ab
K
,
m P 2P
P 2P
ab
aa ab
bb
2
3
4
42,6
42,5
42,4
Laa= (Pab+2Paa)/Pab
Lbb= (Pab+2Pbb)/Pab
p p m
5
6.
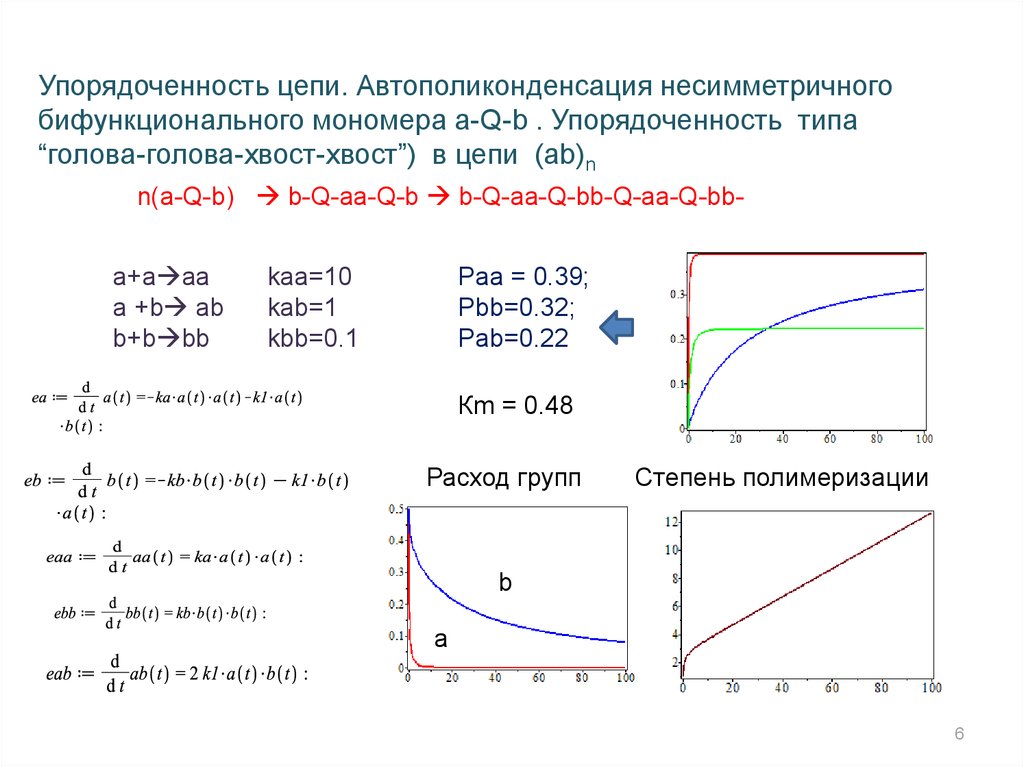
Упорядоченность цепи. Автополиконденсация несимметричногобифункционального мономера a-Q-b . Упорядоченность типа
“голова-голова-хвост-хвост”) в цепи (ab)n
n(a-Q-b) b-Q-aa-Q-b b-Q-aa-Q-bb-Q-aa-Q-bba+a aa
a +b ab
b+b bb
Рaa = 0.39;
Pbb=0.32;
Pab=0.22
kaa=10
kab=1
kbb=0.1
Кm = 0.48
Расход групп
Степень полимеризации
b
а
6
7.
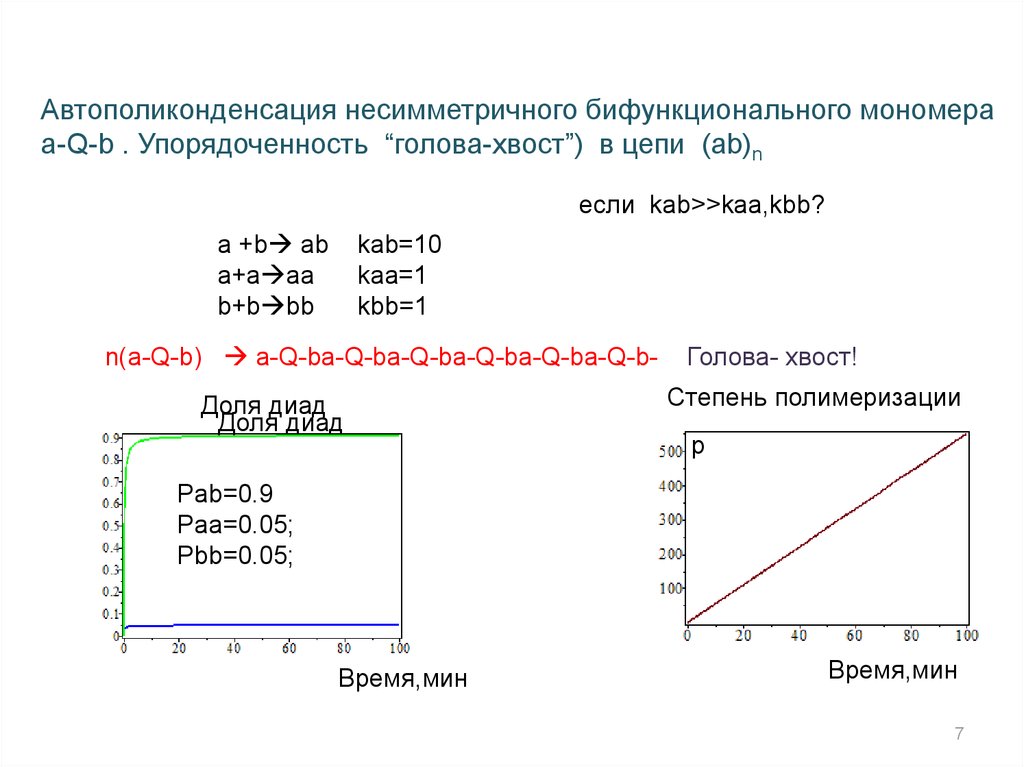
Автополиконденсация несимметричного бифункционального мономераa-Q-b . Упорядоченность “голова-хвост”) в цепи (ab)n
если kab>>kaa,kbb?
a +b ab
a+a aa
b+b bb
kab=10
kaa=1
kbb=1
n(a-Q-b) a-Q-ba-Q-ba-Q-ba-Q-ba-Q-ba-Q-bДоля диад
Доля диад
Голова- хвост!
Степень полимеризации
p
Pab=0.9
Paa=0.05;
Pbb=0.05;
Время,мин
Время,мин
7
8.
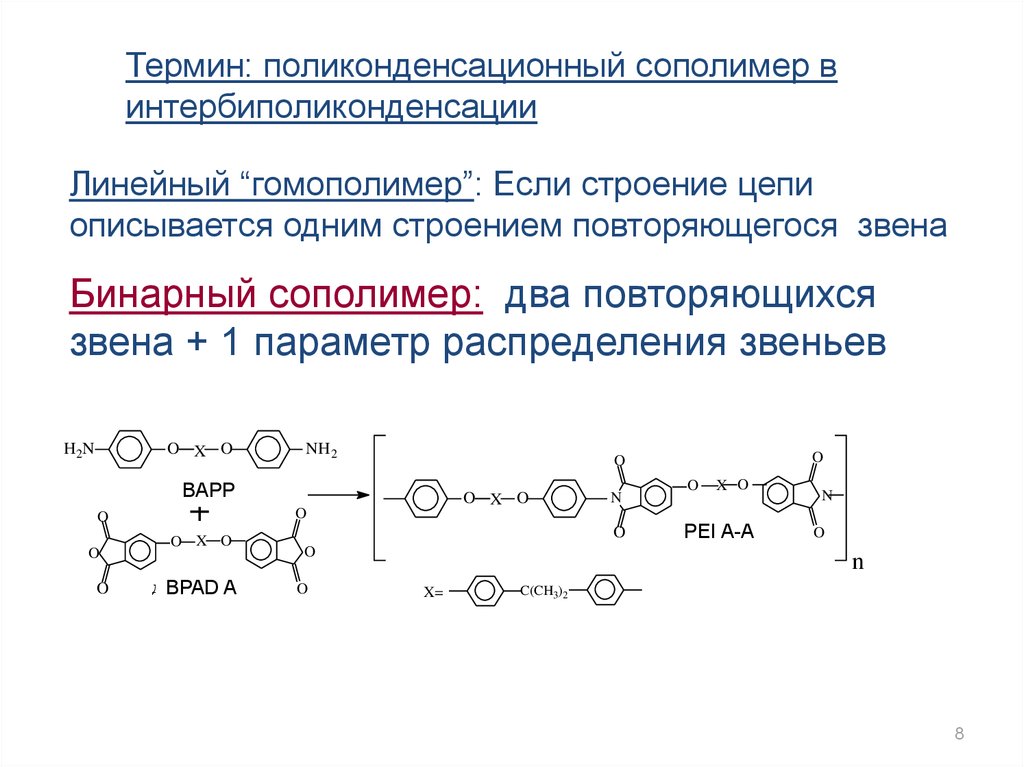
Термин: поликонденсационный сополимер винтербиполиконденсации
Линейный “гомополимер”: Если строение цепи
описывается одним строением повторяющегося звена
Бинарный сополимер: два повторяющихся
звена + 1 параметр распределения звеньев
H2N
O X O
NH 2
диамин
BAPPА
O
O
O
+
O X O
диангидрид
BPAD A А
O X O
O
N
O
O
O
O
O
O
X O
PEI A-A
ПЭИ
А-А
N
O
n
X=
C(CH3)2
8
9.
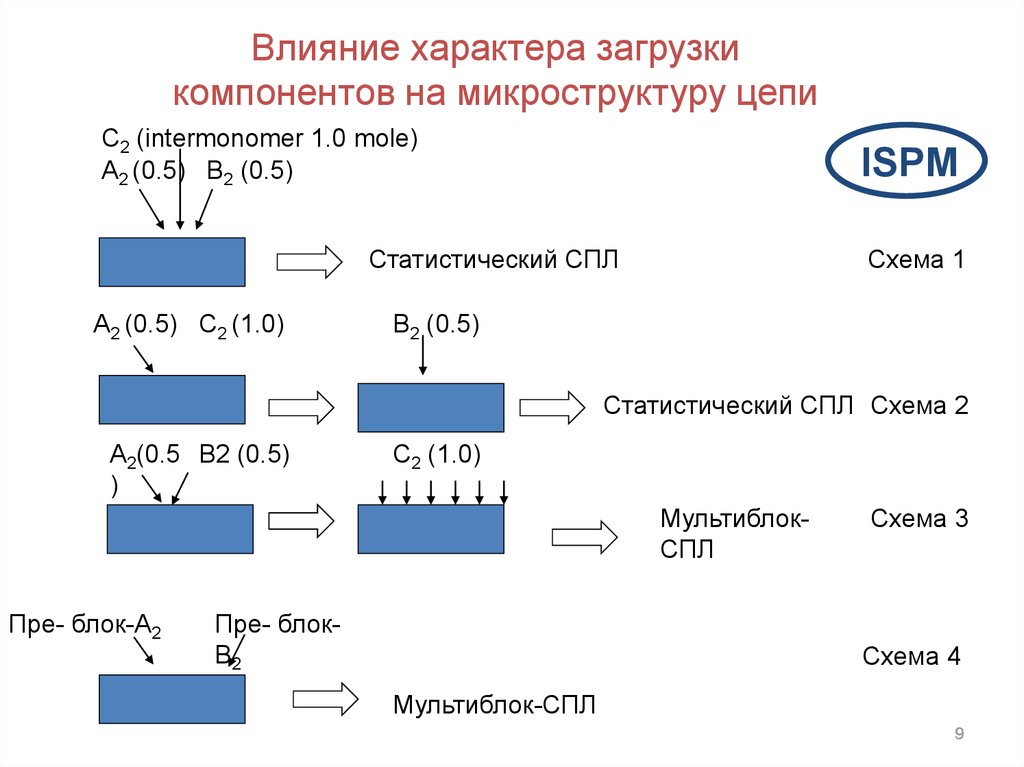
Влияние характера загрузкикомпонентов на микроструктуру цепи
C2 (intermonomer 1.0 mole)
A2 (0.5) B2 (0.5)
ISPM
Статистический СПЛ
A2 (0.5) C2 (1.0)
Схема 1
B2 (0.5)
Статистический СПЛ Схема 2
A2(0.5 B2 (0.5)
)
C2 (1.0)
МультиблокСПЛ
Пре- блок-A2
Пре- блокB2
Схема 3
Схема 4
Мультиблок-СПЛ
9
10.
Теоретический анализ формированиямикроструктуры цепи при идеальной
интербиполиконденсации
(A2+B2 сомономеры)+C2(интермономер)
Васнев В.А., Кучанов С.И, Успехи химии, 1973
Обратимая
сополиконденсация
Необратимая
сополиконденсация
Статистический
Статистический
Блок-СПЛ
Чередующийся СПЛ
В зависимости от отношения реакционной
способности групп и порядка загрузки
10
11.
Условия образования СПЛ с упорядоченноймикроструктурой цепи при необратимой
интербисополиконденсации симметричных мономеров
1. Блок-сополимеры
1) Заметное различие активности сомономеров r = kA1/kB1;
2) “Медленное” введение интермономера С2 к смеси
сомономеров;
3) Отсутствие побочных реакций рандомизации цепи.
2. Чередующиеся сополимеры
1) Различие активности сомономеров;
2) Различие активности 1-ой и 2-ой групп в
интермономере ;
3) Отсутствие побочных реакций рандомизации цепи.
Любые условия, отличные от этих ведут
к статистическому распределению!!
11
Васнев В.А., Кучанов С.И, Успехи химии, 1973
12.
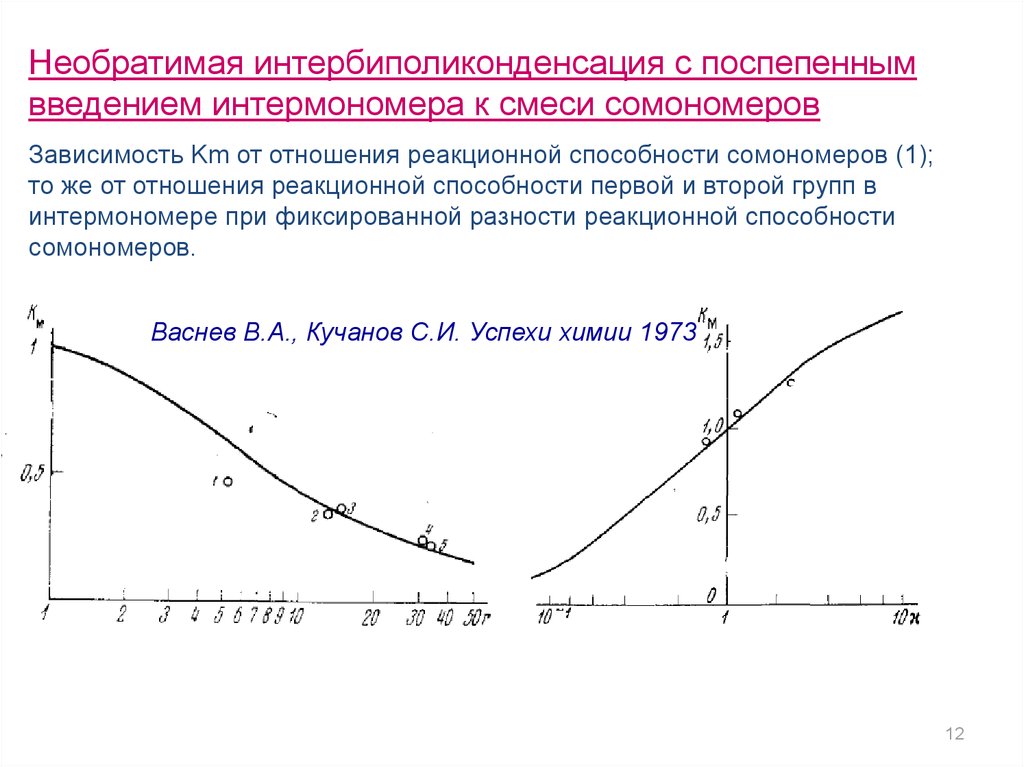
Необратимая интербиполиконденсация с поспепеннымвведением интермономера к смеси сомономеров
Зависимость Km от отношения реакционной способности сомономеров (1);
то же от отношения реакционной способности первой и второй групп в
интермономере при фиксированной разности реакционной способности
сомономеров.
Васнев В.А., Кучанов С.И. Успехи химии 1973
12
13.
Как провести кинетический анализ формирования микроструктуры цепипри сополиконденсации?
Шаг 1. Кинетическая схема и система кин. уравнений.
Шаг 2. Подстановка констант скоростей реакций и начальных
условий
ka11=ka12=k21=k22=5
kb11=kb12=kb21=kb22=1
kraa=krbb=krab=0
s=0.5
a1(0)=1,a2(0)=0,b1(0)=1,b2(0)=0,c1(0)=0,c2a(0)=0,c2b(0)=0,taa(0)=0,tbb(0)=0,tab(0
)=0
Задание режима добавления
t 10
0
мономера,например
10 t and t 11
qb := 0.5
11 t
qb:=piecewise(t<10,0,t>10 and t<11,0.5,t>11,0)
0
0.1
0 t and t 10
qc := {
0
10 t
Шаг 3. Численное интегрирование системы
уравнений с использованием
программыMAPLE 17
S1:=dsolve({ea1,ea2,eb1,eb2,ec1,ec2a,ec2b,etaa,etbb,etab,a1(0)=1,a2(0
)=0,b1(0)=1,b2(0)=0,c1(0)=0,c2a(0)=0,c2b(0)=0,taa(0)=0,tbb(0)=0,tab(0)
=0},fcns,numeric,output=listprocedure):
qc:=piecewise(t>0 and t<10,0.1,t>10,0);
14.
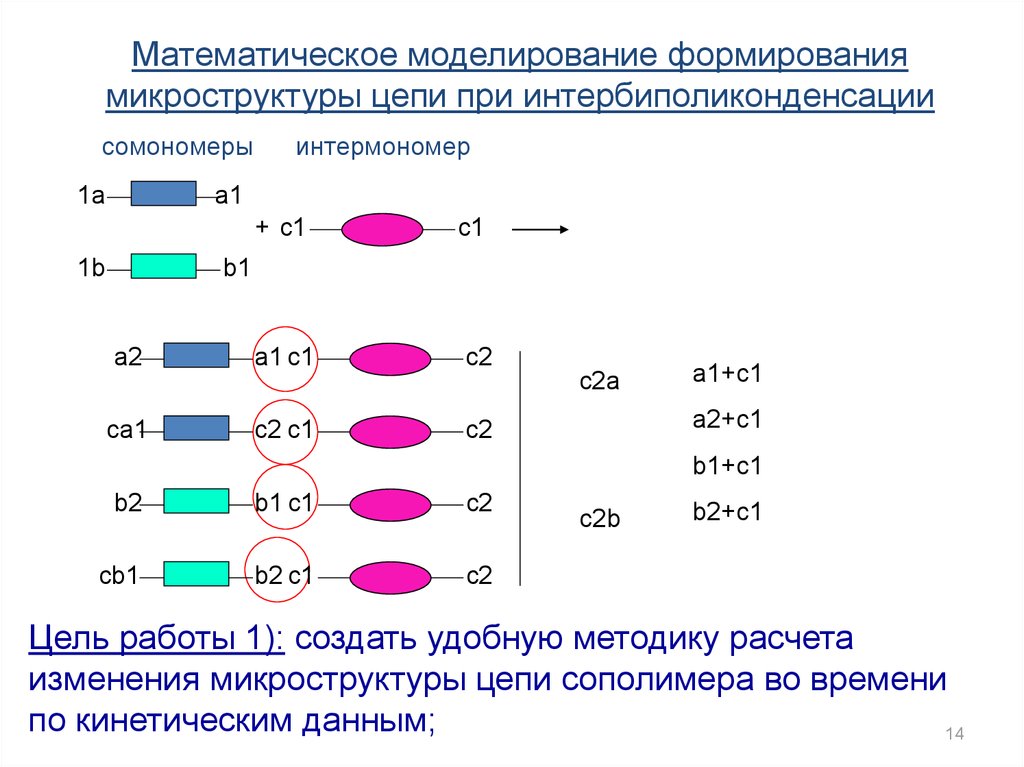
Математическое моделирование формированиямикроструктуры цепи при интербиполиконденсации
сомономеры
1a
интермономер
a1
+ c1
1b
c1
b1
a2
a1 c1
c2
c2a
ca1
c2 c1
a1+c1
a2+c1
c2
b1+c1
b2
b1 c1
c2
cb1
b2 c1
c2
c2b
b2+c1
Цель работы 1): создать удобную методику расчета
изменения микроструктуры цепи сополимера во времени
по кинетическим данным;
14
15.
Образование триад «аса», «bсb», «aсb»a2
a1c1
c2 1a
a2
c1a
a2c1
c2 2a
a1c
c1a
a2c1
c2 a1
a2
2a
a1c1
c21b
b2
c1a
a2c1
с2b
b1c
c1a
a2 c1
c2 1b
b2
ISPM
a1+c2а
a2+c2а
«aсa»
(aa)
a2+c2b
b1+c2а
b1+c2a
«acb»
(ab)
b2+c2a
2b
b1c1
c2 b1
b2
b1+c2b
c1b
b2 c1
c2 b2
b1c
cb1
b2c1
c2 b1
b2
b2+c2b
«bcb»
(bb)
15
16.
Кинетические уравнения для расходованияфункциональных групп и образования триад
etaa :=
etbb :=
d
taa( t ) ka12 a1( t ) c2a( t ) ka22 a2( t ) c2a( t ) kraa taa( t )
dt
d
tbb( t ) kb12 b1( t ) c2b( t ) kb22 b2( t ) c2b( t ) krbb tbb( t )
dt
d
tab( t ) ka12 a1( t ) c2b( t ) ka22 a2( t ) c2b( t ) kb12 b1( t ) c2a( t )
dt
kb22 b2( t ) c2a( t ) krab tab( t )
etab :=
17.
Шаг 1. Составление системы уравнений, описывающейизменение концентраций функциональных групп : a1(t), a2(t),
b1(t), c1(t),c2a(t), c2b(t), and dyads; taa(t), tbb(t), tab(t)
>
1 d
ea1 := a1( t ) ka11 a1( t ) c1( t ) ka12 a1( t ) c2a( t ) ka12 a1( t ) c2b( t )
2 dt
d
ea2 :=
a2( t ) ka11 a1( t ) c1( t ) ka12 a1( t ) c2a( t ) ka12 a1( t ) c2b( t )
dt
ka22 a2( t ) c2a( t ) ka22 a2( t ) c2b( t ) ka21 a2( t ) c1( t ) kraa taa( t )
s krab tab( t )
1 d
eb1 := b1( t ) kb11 b1( t ) c1( t ) kb12 b1( t ) c2a( t ) kb12 b1( t ) c2b( t ) B gb
2 dt
…………………………
1 d
c1( t )
2 dt
ka11 a1( t ) c1( t ) kb11 b1( t ) c1( t ) ka21 a2( t ) c1( t ) kb21 b2( t ) c1( t ) C qc
ec1 :=
d
c2a( t ) ka11 a1( t ) c1( t ) ka21 a2( t ) c1( t ) ka12 a1( t ) c2a( t )
dt
ka22 a2( t ) c2a( t ) kb12 b1( t ) c2a( t ) kb22 b2( t ) c2a( t ) kraa taa( t )
s krab tab( t )
ec2a :=
…………………………
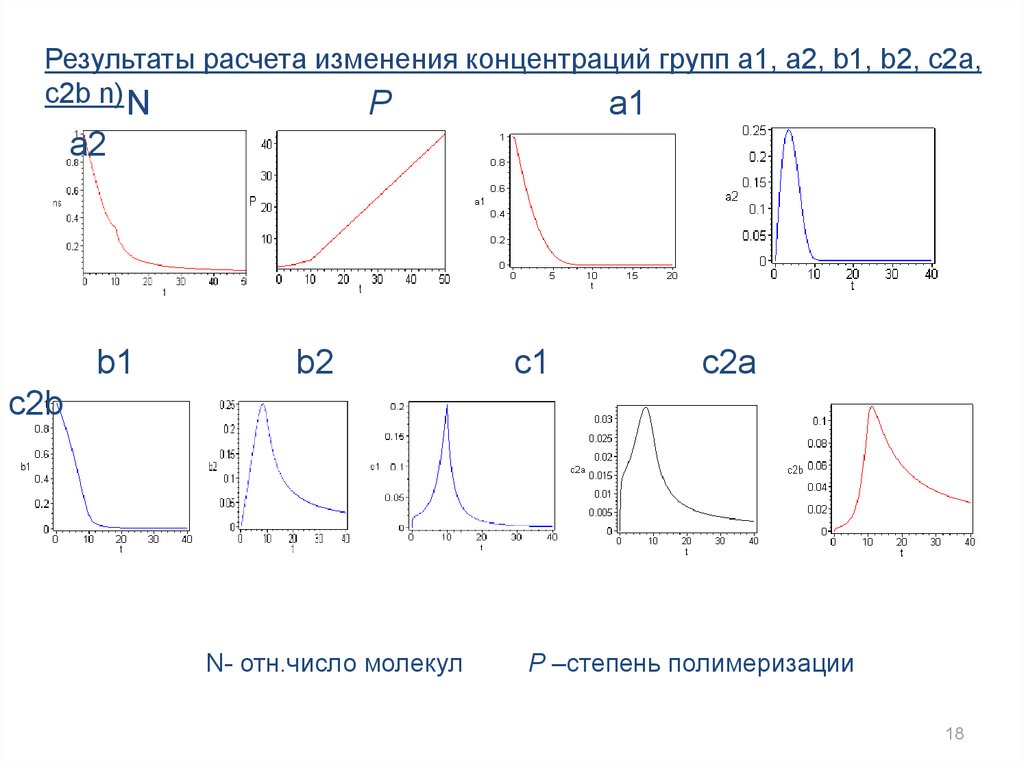
18.
Результаты расчета изменения концентраций групп a1, a2, b1, b2, c2a,c2b n) N
P
a1
a2
b1
b2
c1
c2a
c2b
N- отн.число молекул
P –степень полимеризации
18
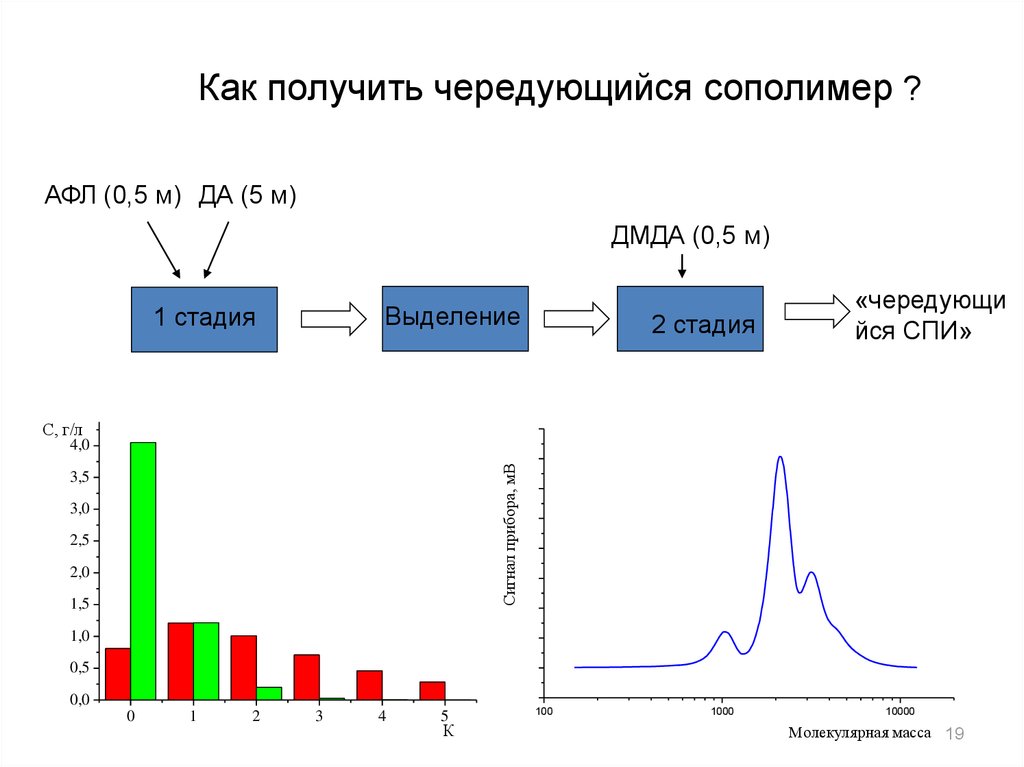
19.
Как получить чередующийся сополимер ?АФЛ (0,5 м) ДА (5 м)
ДМДА (0,5 м)
Выделение
1 стадия
2 стадия
«чередующи
йся СПИ»
C, г/л
Сигнал прибора, мВ
4,0
3,5
3,0
2,5
2,0
1,5
1,0
0,5
0,0
0
1
2
3
4
5
К
100
1000
10000
Молекулярная масса 19
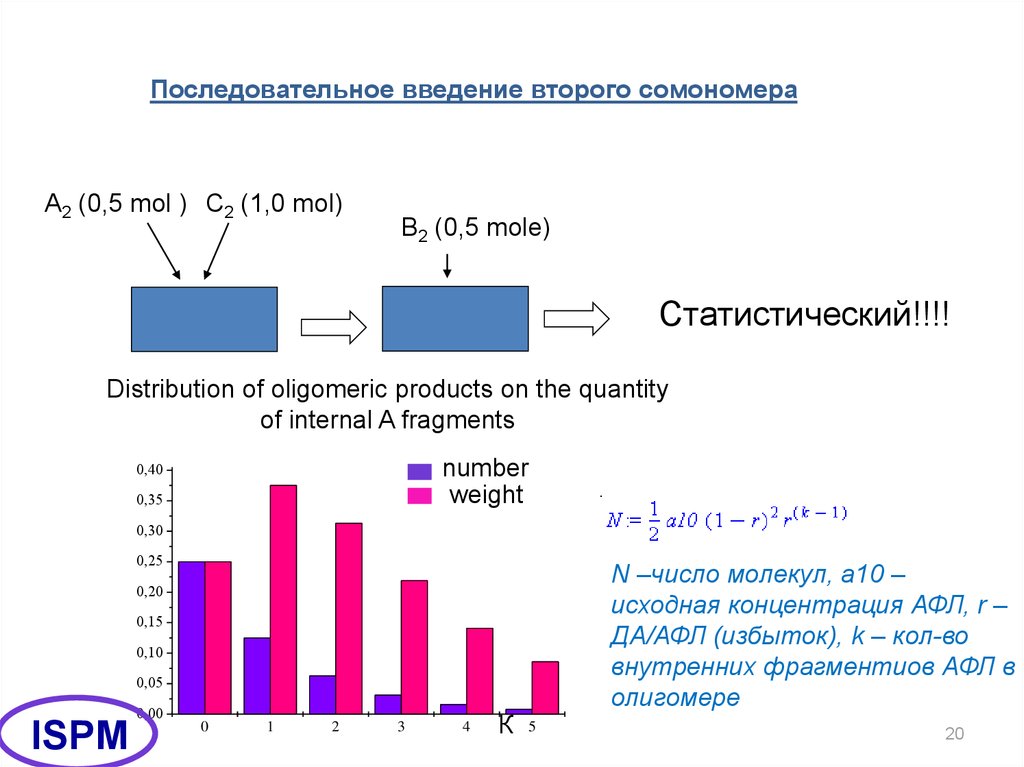
20.
Последовательное введение второго сомономераA2 (0,5 mol ) C2 (1,0 mol)
B2 (0,5 mole)
Статистический!!!!
Distribution of oligomeric products on the quantity
of internal A fragments
number
weight
0,40
0,35
0,30
0,25
N –число молекул, а10 –
исходная концентрация АФЛ, r –
ДА/АФЛ (избыток), k – кол-во
внутренних фрагментиов АФЛ в
олигомере
0,20
0,15
0,10
0,05
ISPM
0,00
0
1
2
3
4
К
5
20
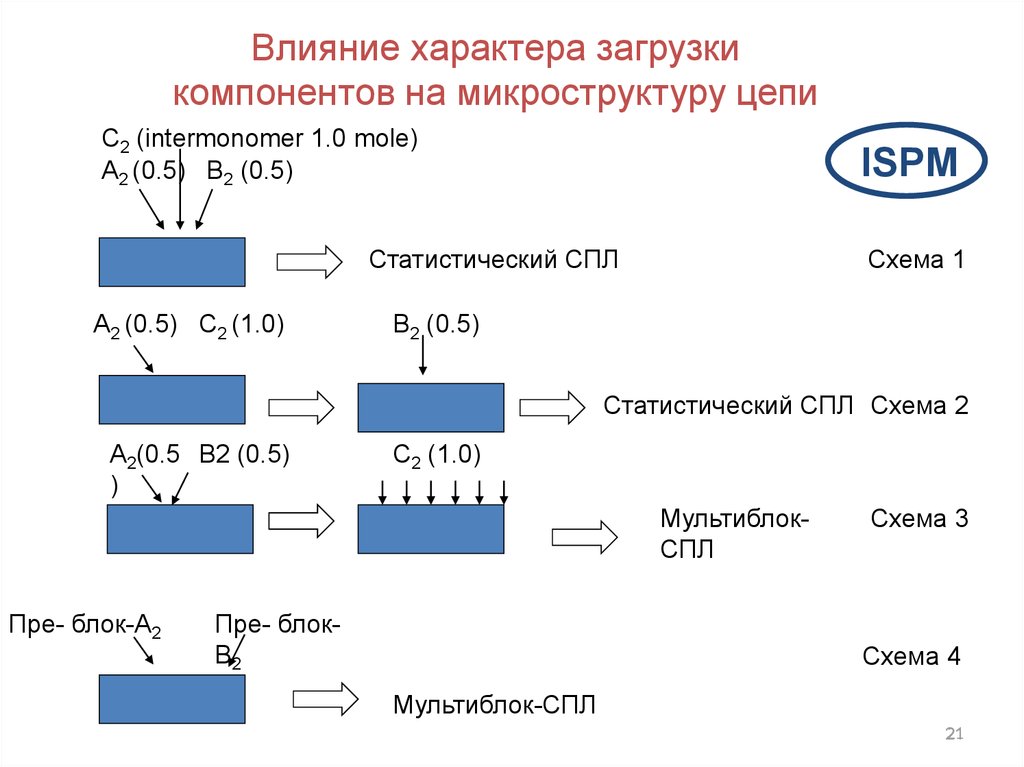
21.
Влияние характера загрузкикомпонентов на микроструктуру цепи
C2 (intermonomer 1.0 mole)
A2 (0.5) B2 (0.5)
ISPM
Статистический СПЛ
A2 (0.5) C2 (1.0)
Схема 1
B2 (0.5)
Статистический СПЛ Схема 2
A2(0.5 B2 (0.5)
)
C2 (1.0)
МультиблокСПЛ
Пре- блок-A2
Пре- блокB2
Схема 3
Схема 4
Мультиблок-СПЛ
21
21
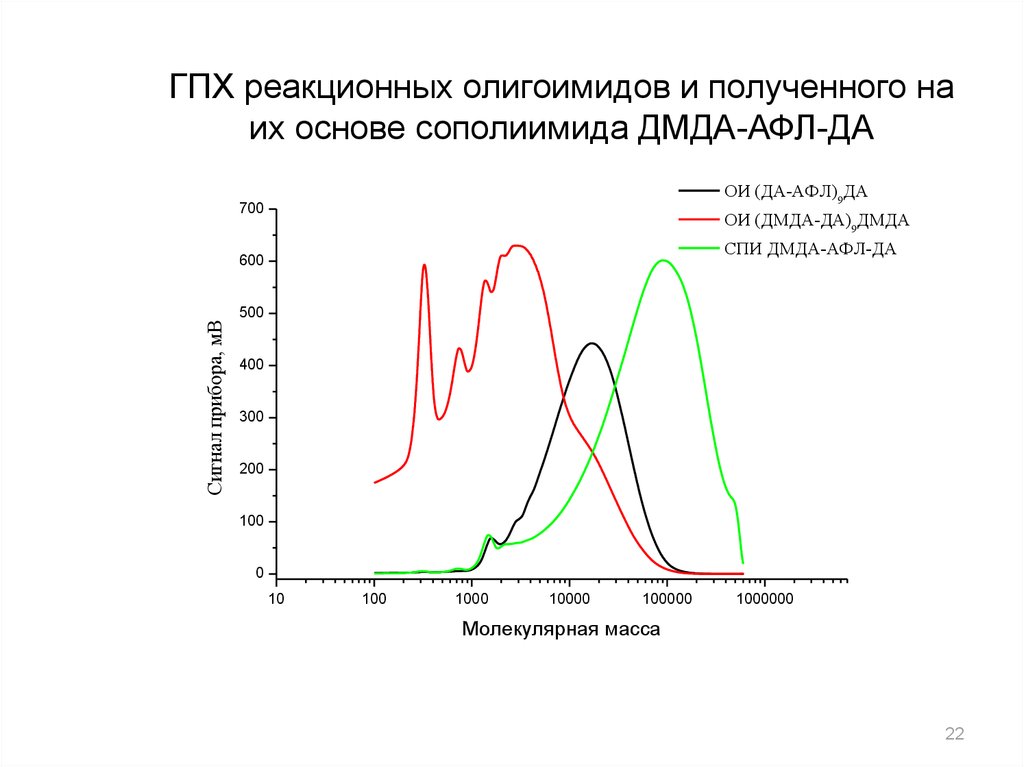
22.
ГПХ реакционных олигоимидов и полученного наих основе сополиимида ДМДА-АФЛ-ДА
ОИ (ДА-АФЛ)9ДА
700
ОИ (ДМДА-ДА)9ДМДА
СПИ ДМДА-АФЛ-ДА
Сигнал прибора, мВ
600
500
400
300
200
100
0
10
100
1000
10000
100000
1000000
Молекулярная масса
22
23.
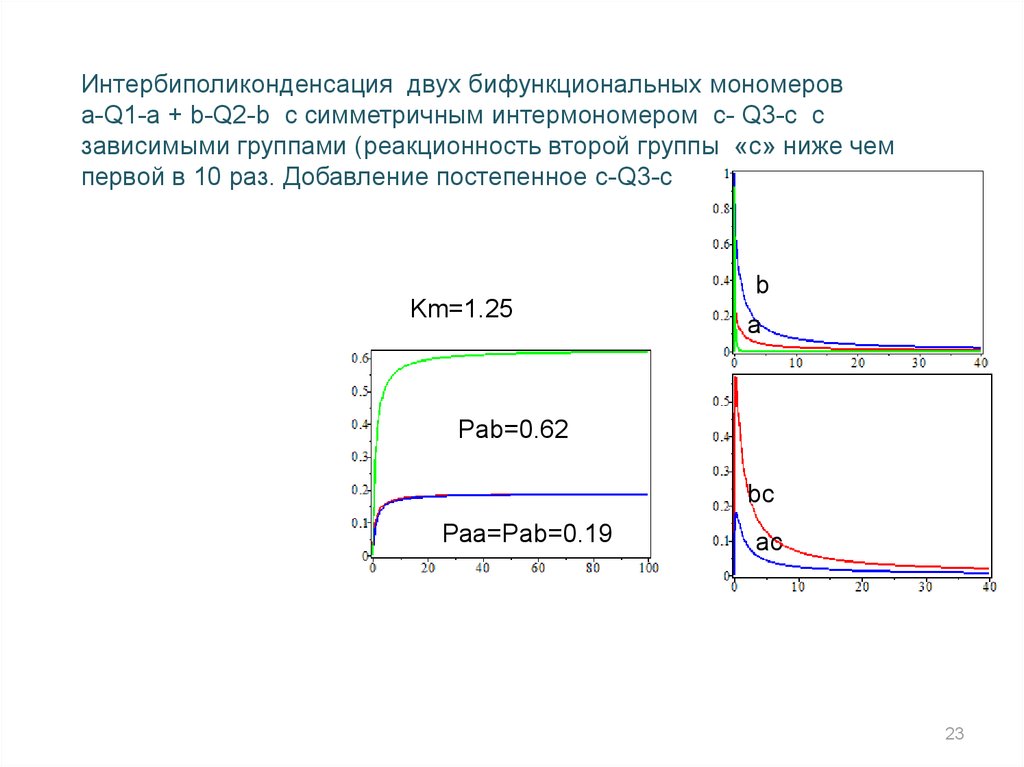
Интербиполиконденсация двух бифункциональных мономеровa-Q1-a + b-Q2-b с симметричным интермономером с- Q3-c c
зависимыми группами (реакционность второй группы «с» ниже чем
первой в 10 раз. Добавление постепенное c-Q3-c
b
Km=1.25
a
Рab=0.62
bc
Раа=Pab=0.19
ac
23
24.
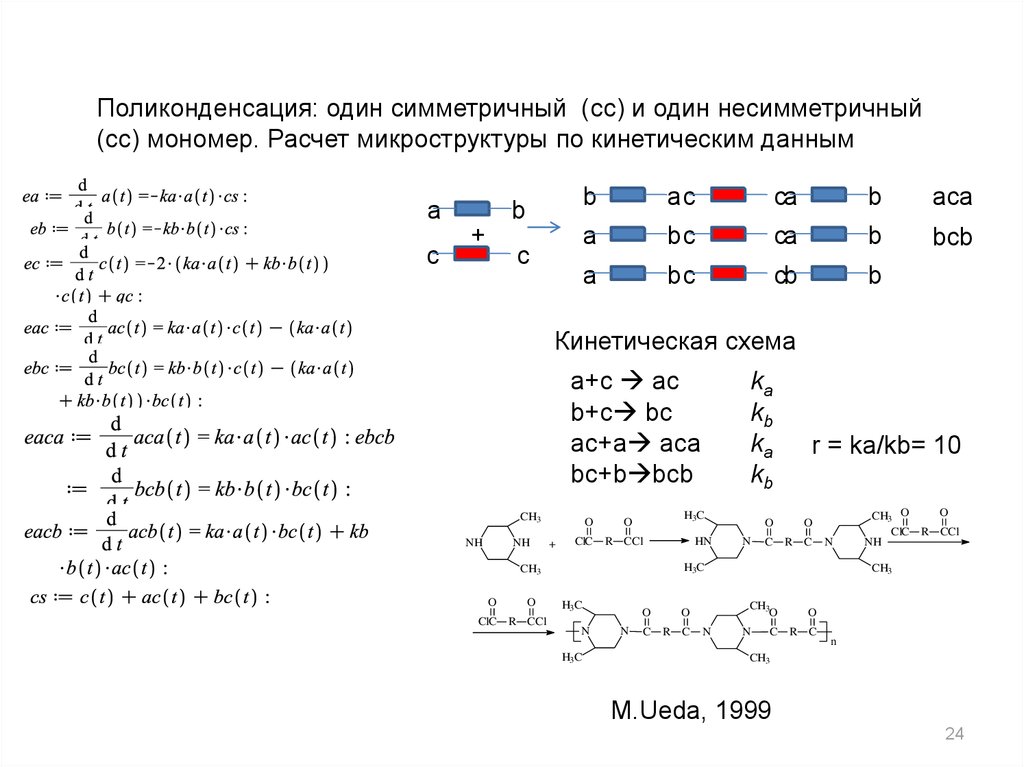
Поликонденсация: один симметричный (cc) и один несимметричный(cc) мономер. Расчет микроструктуры по кинетическим данным
a
c
b
+
c
b
ac
ca
b
aca
a
bc
ca
b
bcb
a
bc
cb
b
Кинетическая схема
a+c ac
b+c bc
ac+a aca
bc+b bcb
CH3
NH
NH
O
+
ClC
H3C
O
R CCl
O
O
R CCl
HN
N
r = ka/kb= 10
O
O
C
R C
N
H3C
CH3
ClC
ka
kb
ka
kb
H3C
N
H3C
N
O
O
C
R C
N
CH3 O
ClC
NH
O
R CCl
CH3
CH3
O
O
C
R C
N
n
CH3
M.Ueda, 1999
24
25.
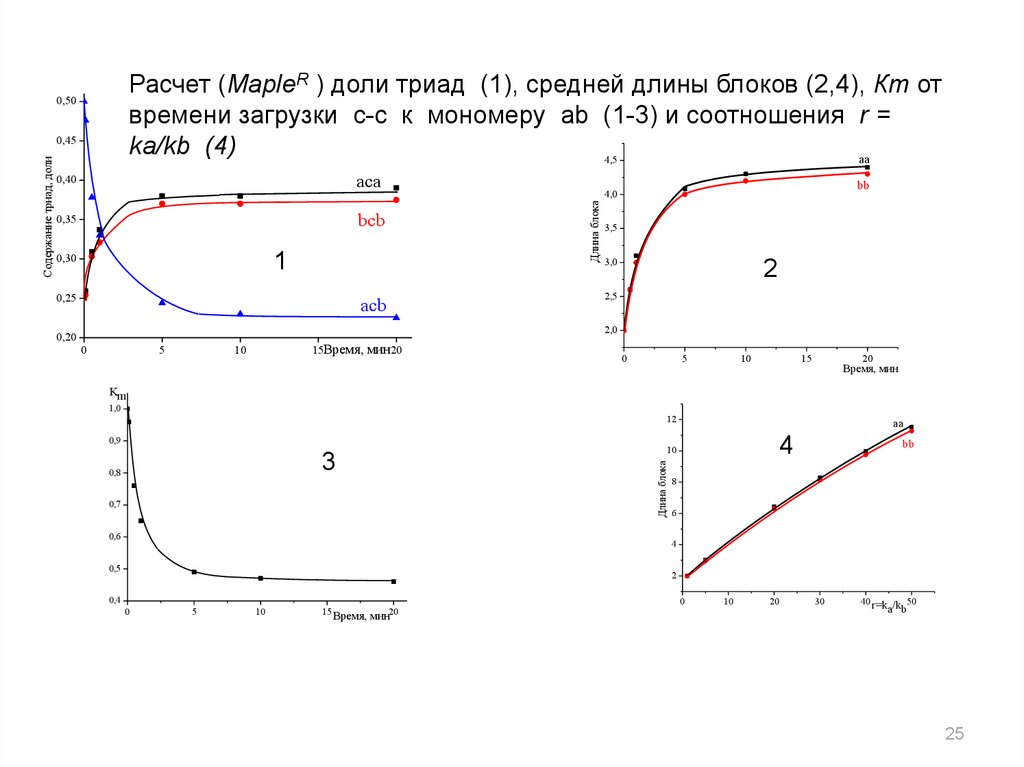
Расчет (MapleR ) доли триад (1), средней длины блоков (2,4), Кm отвремени загрузки c-c к мономеру ab (1-3) и соотношения r =
ka/kb (4)
4,5
aa
0,50
aca
0,40
bcb
0,35
1
0,30
0,25
acb
bb
4,0
Длина блока
3,5
3,0
2
2,5
2,0
0,20
0
5
15Время,
10
мин20
0
5
10
15
20
Время, мин
Km
1,0
12
0,9
3
0,8
0,7
0,6
aa
4
10
Длина блока
Содержание триад, доли
0,45
bb
8
6
4
0,5
2
0,4
0
5
10
15
Время, мин20
0
10
20
30
40 r=k /k 50
a b
25
26.
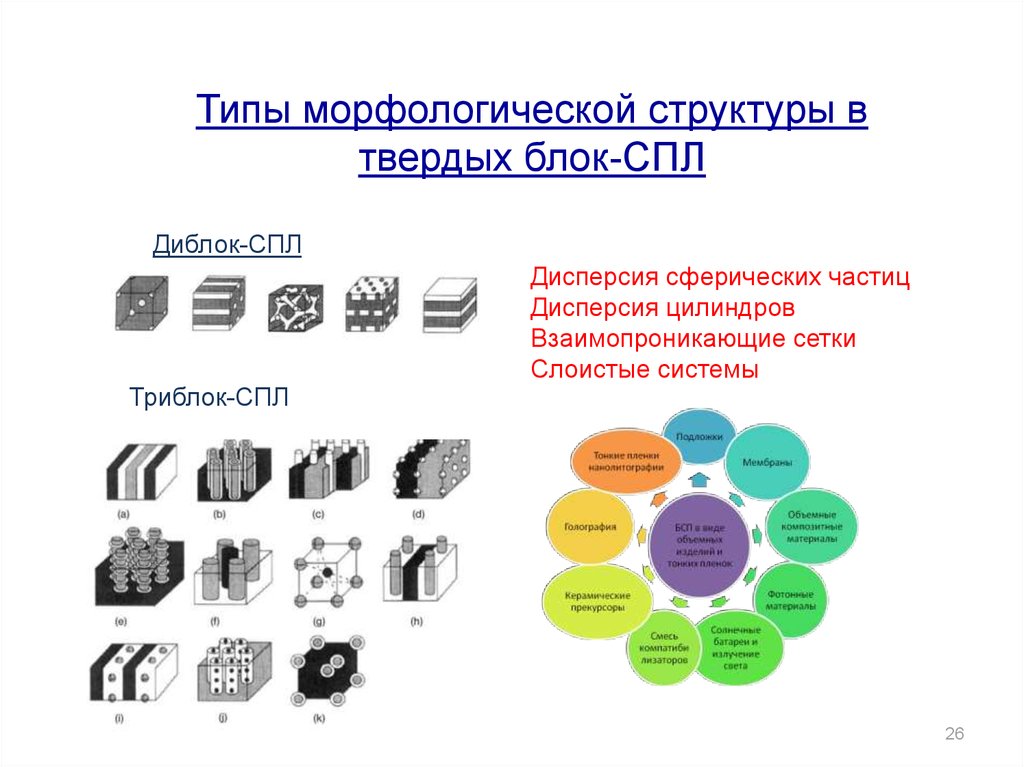
Типы морфологической структуры втвердых блок-СПЛ
Диблок-СПЛ
Триблок-СПЛ
Дисперсия сферических частиц
Дисперсия цилиндров
Взаимопроникающие сетки
Слоистые системы
26
27.
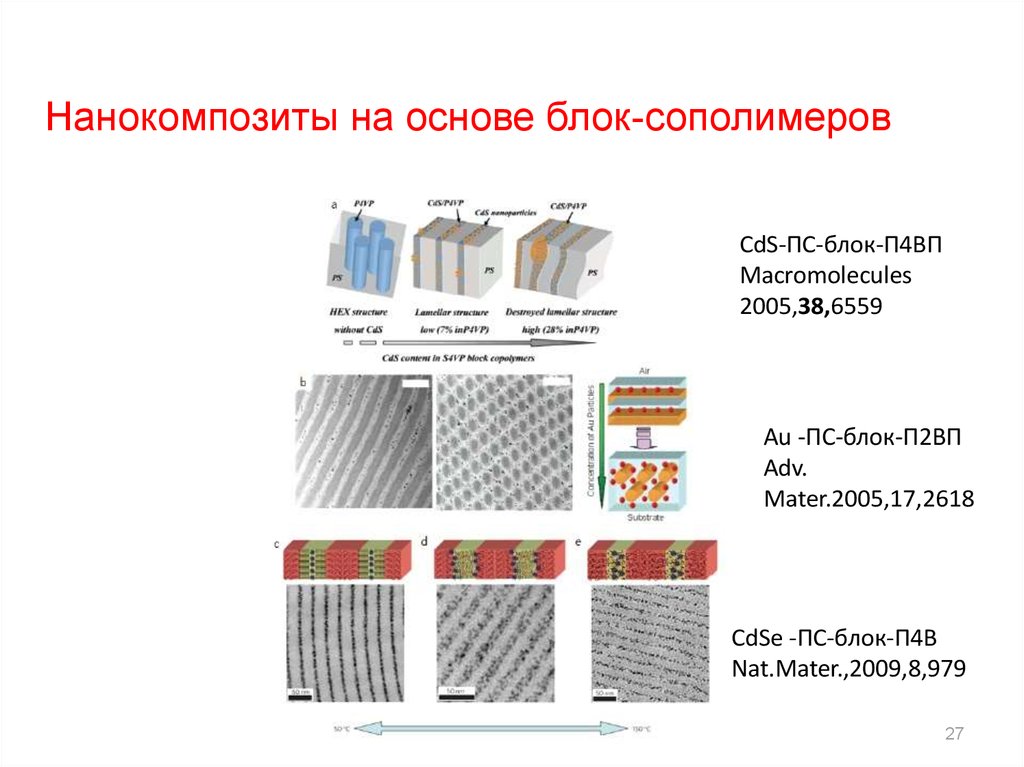
Нанокомпозиты на основе блок-сополимеровCdS-ПС-блок-П4ВП
Macromolecules
2005,38,6559
Au -ПС-блок-П2ВП
Adv.
Mater.2005,17,2618
CdSe -ПС-блок-П4В
Nat.Mater.,2009,8,979
27
28.
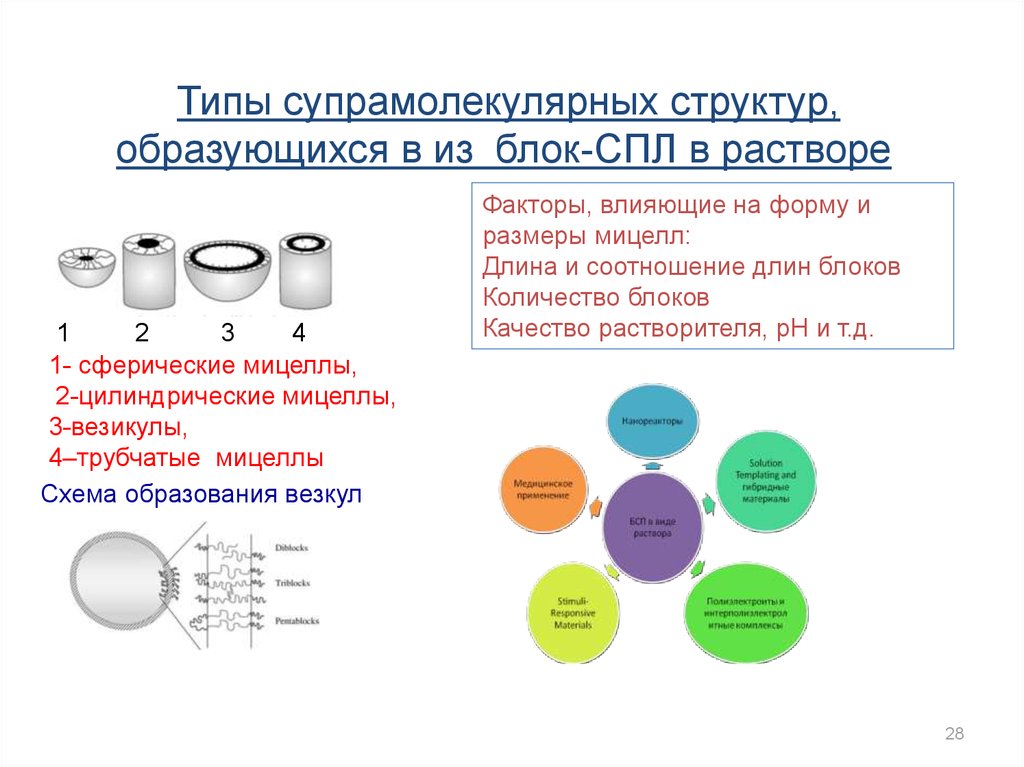
Типы супрамолекулярных структур,образующихся в из блок-СПЛ в растворе
1
2
3
4
1- сферические мицеллы,
2-цилиндрические мицеллы,
3-везикулы,
4–трубчатые мицеллы
Схема образования везкул
Факторы, влияющие на форму и
размеры мицелл:
Длина и соотношение длин блоков
Количество блоков
Качество растворителя, рН и т.д.
28
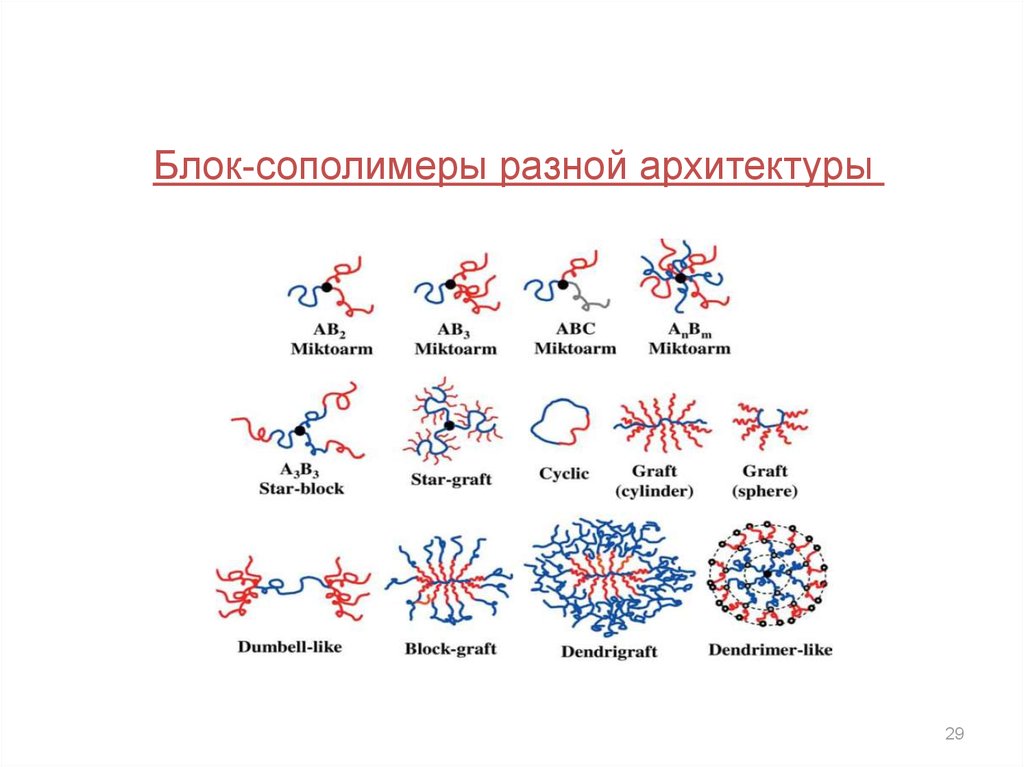
29.
Блок-сополимеры разной архитектуры29
30. Заключение
• При конструировании макромолекул можно использоватьпрограммное обеспечение для экономии времени
эксперимента.
• Блок-СПЛ открывают новые горизонты при создании
новых материалов для электроники, мембранных
технологий, медицины и т.д
30











 Физика
Физика Химия
Химия








