Похожие презентации:
Системы линейных дифференциальных уравнений
1. Математика 2 семестр
Лекция 14Системы линейных
дифференциальных уравнений
2.
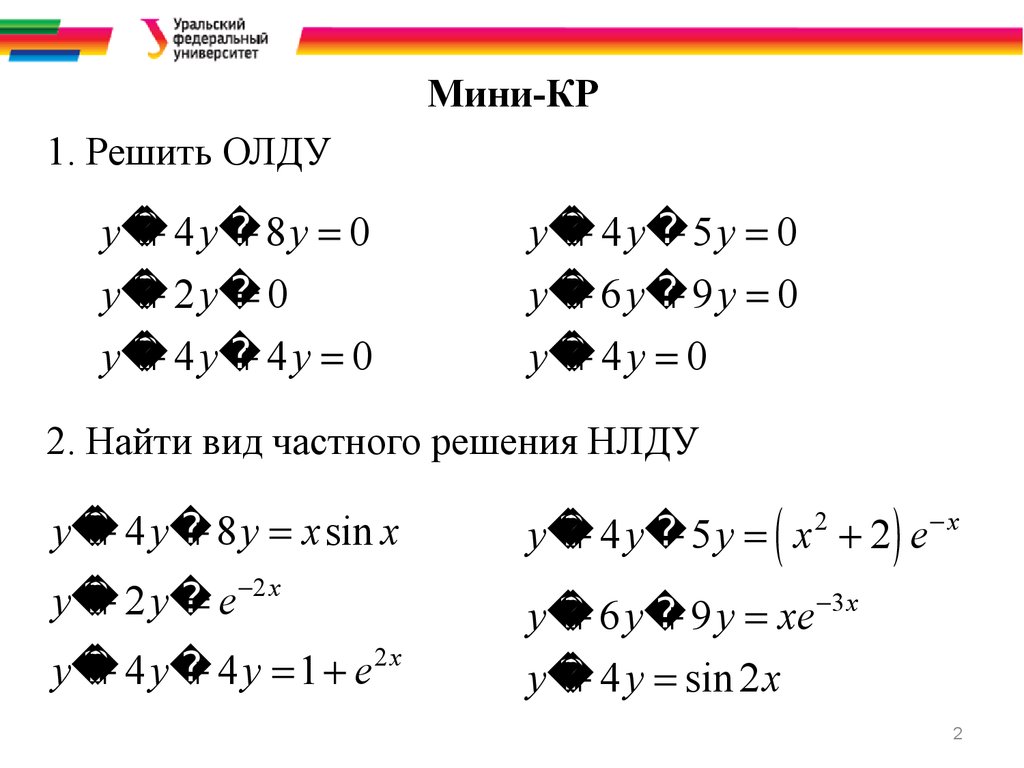
Мини-КР1. Решить ОЛДУ
y
4 y
8y 0
y
2 y
0
y
4 y
5y 0
y
6 y
9y 0
y
4 y
4y 0
y
4y 0
2. Найти вид частного решения НЛДУ
y
4 y
8 y x sin x
2 x
y 2y e
2x
y 4y 4y 1 e
y
4 y
5 y x 2 2 e x
y
6 y
9 y xe 3 x
y
4 y sin 2 x
2
3.
Введение•Существуют методы решения систем
дифференциальных уравнений, сходные с теорией
решения ЛДУ.
3
4.
Основные понятия теории СЛДУОпределение. Нормальная система ДУ называется
линейной, если в каждом ее уравнении функции
xi
t fi t , x1 t , K , xn t ; i 1, n линейны относительно
неизвестных функций, т. е. если она имеет вид:
n
dxi
aij x j bi (t ), i 1, n.
dt
j 1
Запишем систему в векторной форме: x& A t x B t ,
T
где x x1 t , K , xn t .
При B t 0 получим систему ОЛДУ вида x& A t x
t a, b
4
5.
Свойства решений СОЛДУОбозначим через Y множество всех решений СОЛДУ,
Y – линейное пространство.
5
6.
Теорема о структуре общего решения СОЛДУ6
7.
Теорема о структуре общего решения СНЛДУn
Если 1) xk t - ФСР СОЛДУ
x& A t x ;
k 1
2) t – некоторое решение СНЛДУ x& A t x B t ,
то общее решение СНЛДУ находится по формулам:
n
xобщ. СНЛДУ t xобщ. СОЛДУ t t ck xk t t
k 1
или xобщ. СНЛДУ t t c t , t a, b .
Для поиска частного решения t можно
воспользоваться методом вариации произвольной
постоянной (из СОЛДУ):
t t c t .
7
8.
t0A t x B t , имеет решение t t c t .
СНЛДУ x
Тогда
t
t c t t c
t , т.е.
t c t t c
t A t c t B t
t A t , то t c
t B t .
Т.к.
1
c
t
t B t .
Отсюда
t
1
c
t
B d ,
Проинтегрируем обе части:
t
t0 – любое число (a,b).
t
0
t t
1 B d .
t0
t
1
x
t
t
c
t
B d Т.О. общ СНЛДУ
t0
формула Коши.
8
9.
910. ОСЛДУ с постоянными коэффициентами
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
‚ 1 1sin t
X
,
X
2 0 0
τ
X
0
0;
0
.
x%
i t e t Rmi s t cos t Tmi s t sin t , i 1, n
25.
26.
27.
4. Найти общее решение СНЛДУ используя методЭйлера для СОЛДУ и подбор решений для СНЛДУ
27
28.
2829.
2930.
5. Найти общее решение СОЛДУ методом Эйлера1
1
x.
x&=
- 2 - 1
30
31.
3132.
6. Найти общее решение СОЛДУ методом Эйлера2
1
x.
x&=
0
1
32
33.
3334.
7. Решить СНЛДУ по формуле Коши2
3
t
&
x =
x +
,
6 - 1
3
T
x ( 0) = ( 1, 0)
34
35.
3536.
3637.
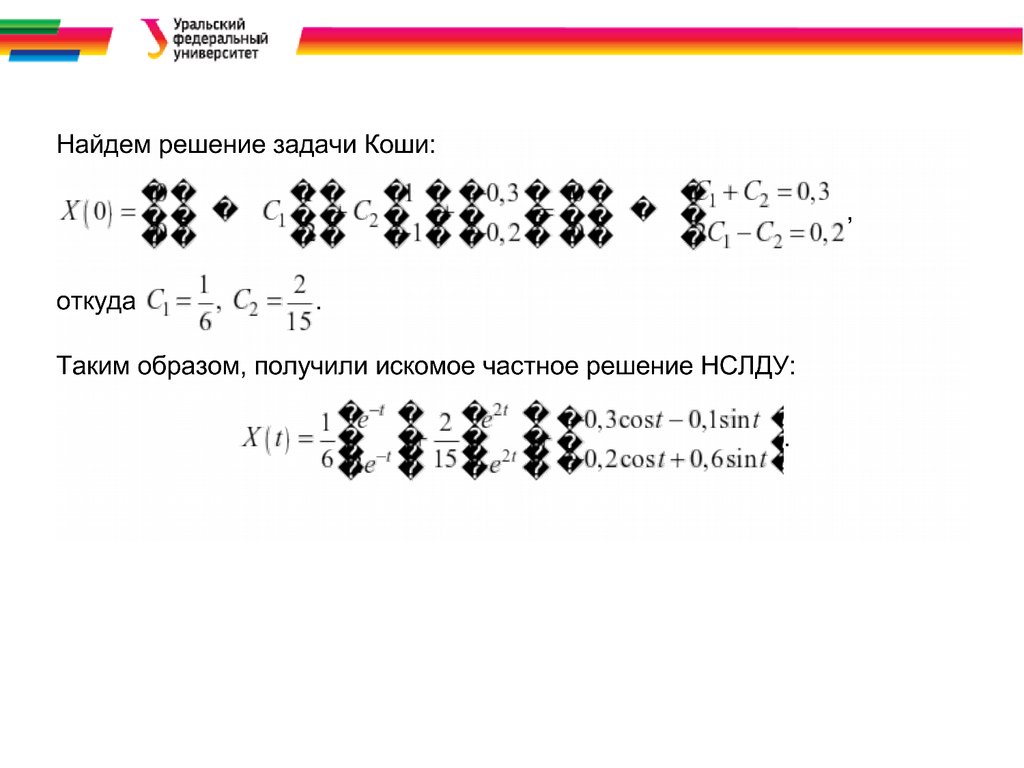
Формула Кошиt
xобщ СНЛДУ t t c t
1 B d
t0
37





































 Математика
Математика








