Функции у = хn (n є N), их свойства и графики

1. Функции у = хn (n є N), их свойства и графики

28.12.11.
Функции у = хn (n є N), их
свойства и графики

2. ЗАДАНИЕ НА ДОМ

§
12,
№ 12.14.(а);
№ 12.18. (б);
№ 12.19. (г).

3. ОПРЕДЕЛЕНИЕ

Функцию вида у = хn, где n = 1,
2, 3, 4, 5, ..., называют
степенной функцией с
натуральным показателем.

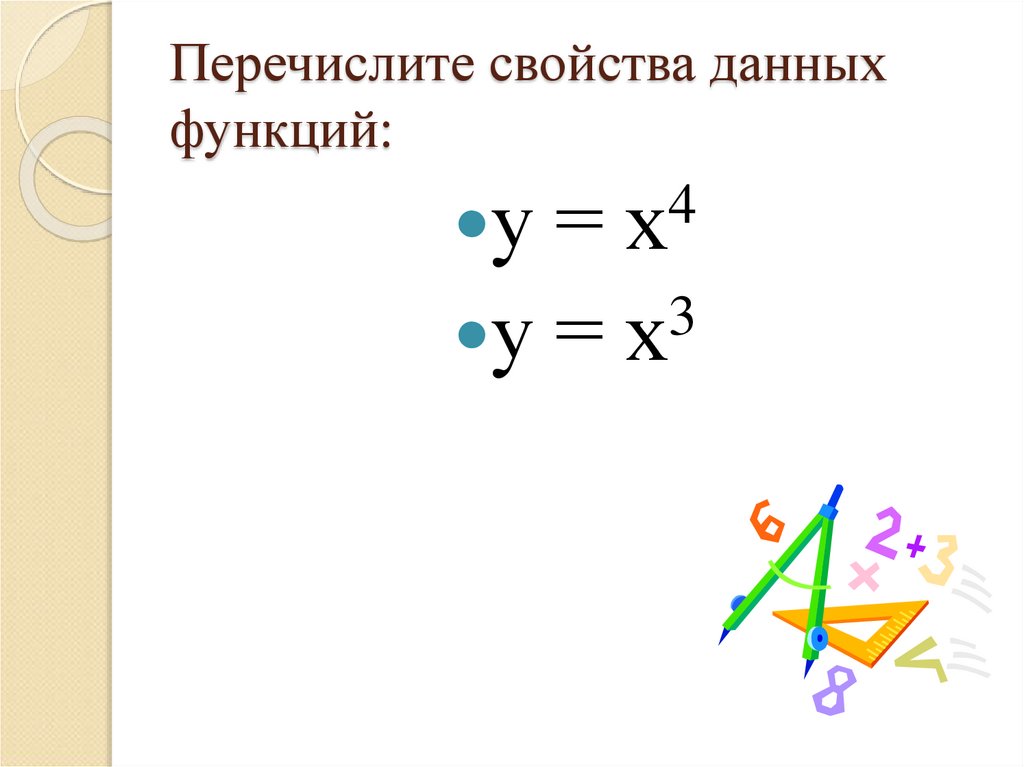
4. Перечислите свойства данных функций:

4
у = х
у
=
3
х

5. у = х4

у=
х
у
4
х
Составим таблицу значений для этой
функции:
0
0
1
1
1/2 2
3/2
1/16 16 81/16

6. у = х4

у=
4
х
Построим точки на координатной
плоскости
они намечают некоторую линию,
проведем ее.

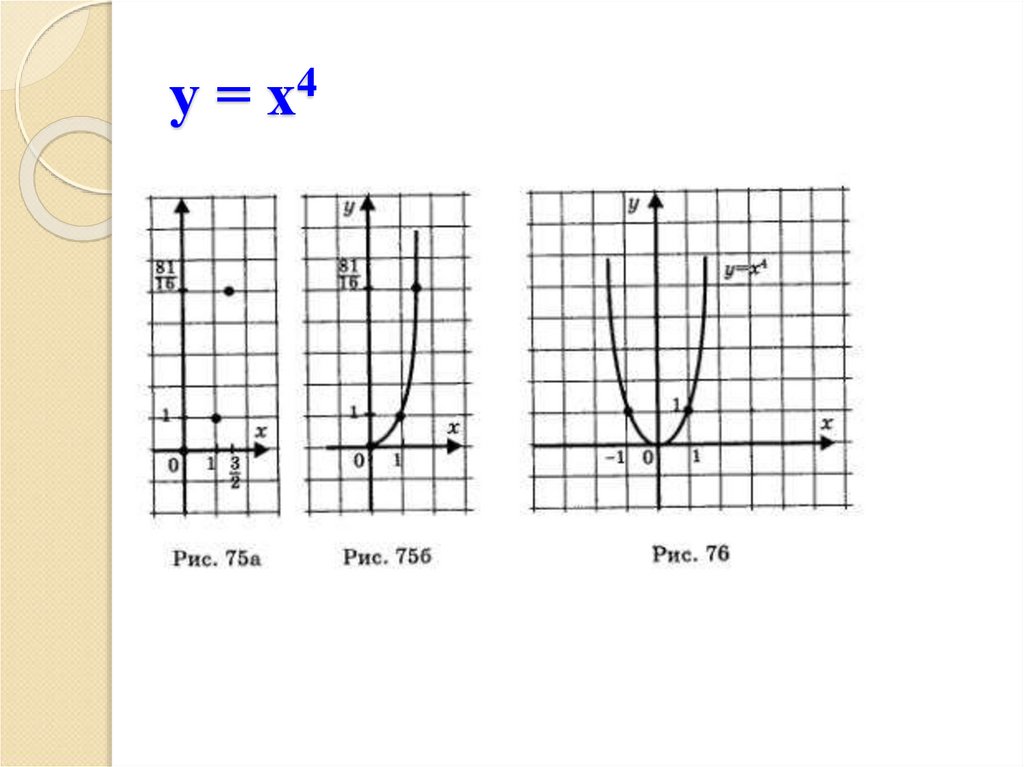
7. у = х4

8. Свойства функции у = х4:

Свойства функции у =
4
х1. D(у)
: = (-∞,+∞);
2.
3.
4.
5.
6.
7.
8.
четная функция;
убывает(-∞, 0], возрастает [0; +∞) ;
Ограничена снизу, не ограничена
сверху;
У наим.= 0, У наиб. нет;
непрерывна;
Е(у) = [0, +∞);
выпукла вниз.

9. Функция у = х2n

Речь идет о функциях у = х6, у = х8 и
вообще о степенной функции счетным
показателем степени.
График любой такой функции похож на
график функции у = х4, только его
ветви более круто направлены вверх.
Отметим еще, что кривая у = х2n касается
оси х в точке (0; 0), т.е. одна ветвь кривой
плавно переходит в другую, как бы
прижимаясь к оси х.

10. у = х3 

у=
х
у
3
х
Составим таблицу значений для этой
функции:
0
0
1
1
1/2
1/8
2
8
3/2
27/8

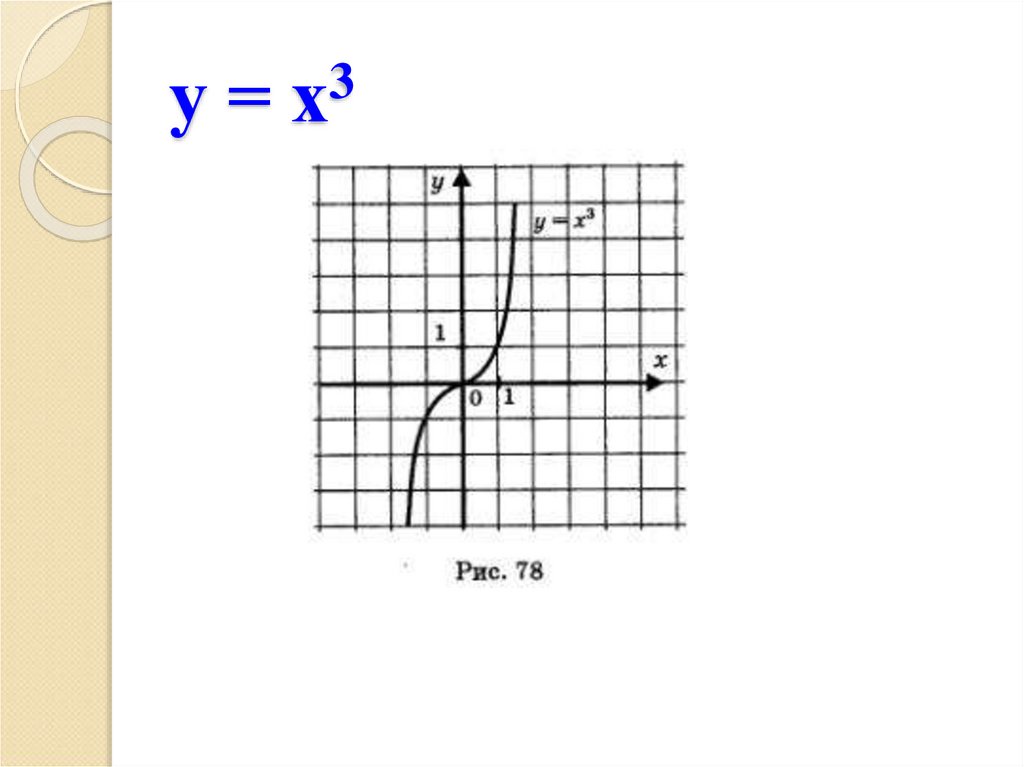
11. у = х3 

у=
3
х

12. Свойства функции у = х3 

Свойства функции у =
3
х
D(у) = (-∞,+∞);
2. нечетная функция;
3. возрастает;
4. не ограничена ни снизу, ни сверху;
5. нет ни наименьшего, ни наибольшего
значений;
6. непрерывна;
7. Е(у) = (-∞, +∞);
8. выпукла вверх при х < 0, выпукла вниз
при х > 0.
1.

13. Функция у = х2n+1

Речь идет о функциях у = х3, у = х5 и
вообще о степенной функции с нечетным
показателем степени (3, 5, 7, 9 и т.д.).
• График любой такой функции похож на
график у = х3 функции только чем
больше показатель, тем более круто
направлены вверх (и соответственно
вниз) ветви графика.
• Отметим еще, что кривая у =х2n+1 касается
оси х в точке (0; 0).

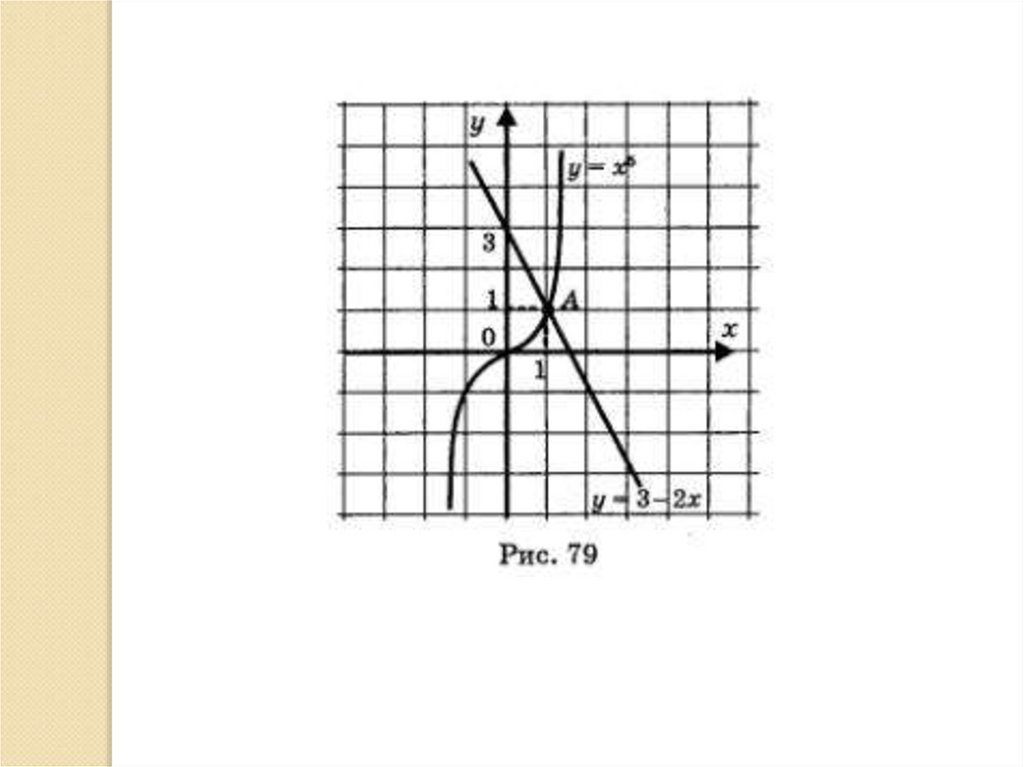
14. Пример 1. Решить уравнение:  

Пример 1. Решить уравнение:
5
х
= 3 - 2х.