Тренинговая работа №3

1. Тренинговая работа №3

Работа учителя математики
Моисеевой Нины Ивановны

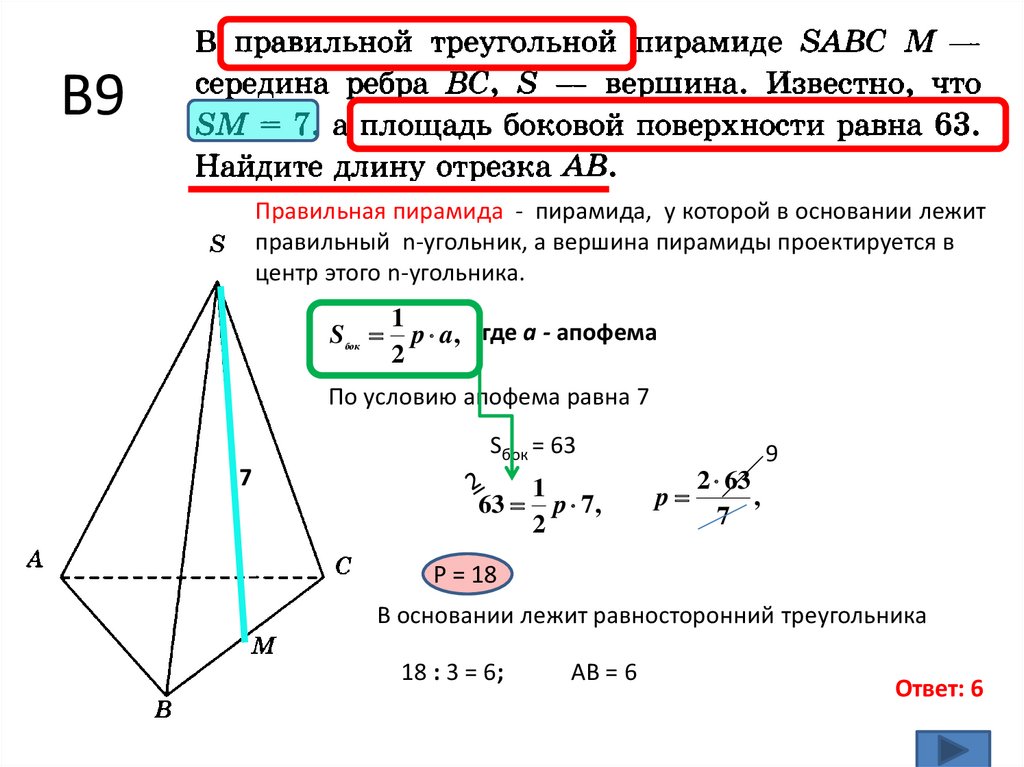
2. В9

Правильная пирамида - пирамида, у которой в основании лежит
правильный n-угольник, а вершина пирамиды проектируется в
центр этого n-угольника.
S
бок
1
p a , где а - апофема
2
По условию апофема равна 7
Sбок = 63
7
1
63 p 7,
2
p
2 63
,
7
9
Р = 18
В основании лежит равносторонний треугольника
18 : 3 = 6;
АВ = 6
Ответ: 6

3.

d =3
3
Sбок. = 2 π R H = π d H
Sбок. = 12π
12π
Sбок. = π d H
12 π = π 3 H
12 = 3 H
H=4
Ответ: 4

4. B9

Все боковые ребра правильной пирамиды равны, а боковые
грани являются равнобедренными треугольниками
Площадь боковой поверхности равна 3·SΔSBC
168
S 168 3 S 168;
S
S
;
3
SBC
бок
бок
56.
SBC
7
SBC
В основании лежит правильный треугольник, у которого
все стороны равны 7
56 2 7 SK ;
7
SK
BC SK
56
;
S
;
SK 16.
2
2
7
S
SBC
Можно воспользоваться формулой:
P
3 7
l , ( l - апофема SK ); 168
SK ,
2
2
SK 16.
Ответ: 16

5. В9

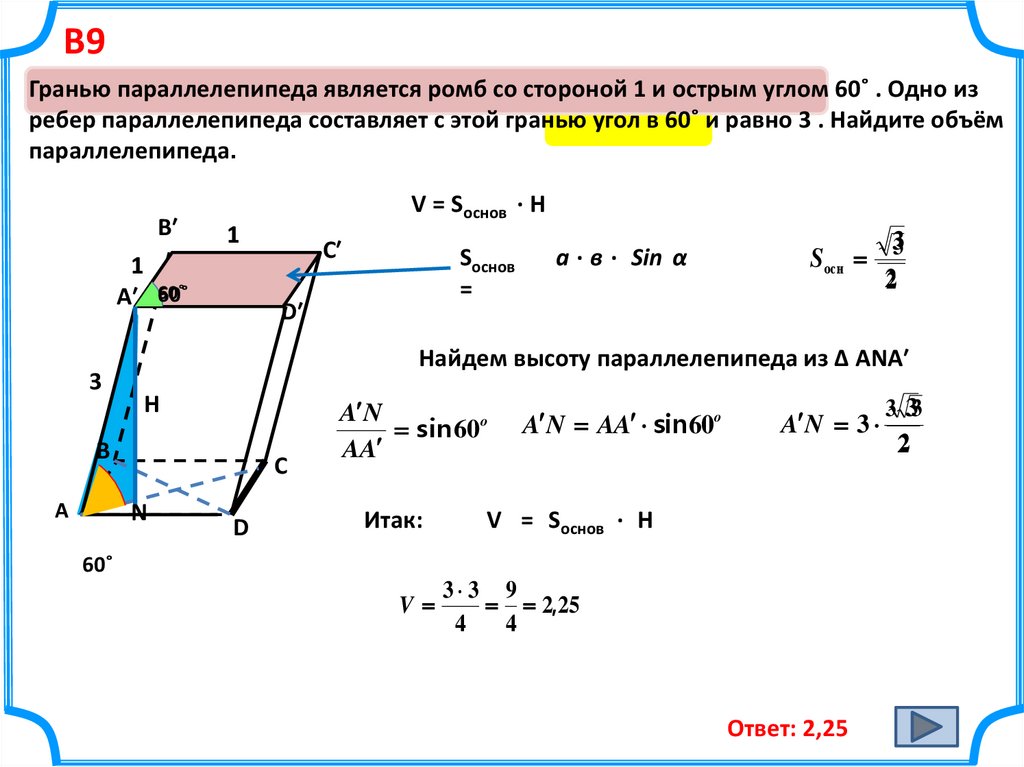
Гранью параллелепипеда является ромб со стороной 1 и острым углом 60˚ . Одно из
ребер параллелепипеда составляет с этой гранью угол в 60˚ и равно 3 . Найдите объём
параллелепипеда.
B′
V = Sоснов · Н
1
1
60˚
A′ 60˚
3
Sоснов
=
D′
а · в · Sin α
3
Sосн 3
2
Найдем высоту параллелепипеда из ∆ ANA′
H
В
А
C′
С
N
D
A N
sin 60o
AA
Итак:
60˚
V
A N AA sin 60o
A N 3
V = Sоснов · Н
3 3 9
2,25
4
4
Ответ: 2,25
3 33
2

6. В10

Число всех возможных исходов – это N = 10 (все свободных машин).
Число благоприятных исходов – это N(A) = 1 (по вызову придет желтое такси).
Вероятность находим, как отношение благоприятных исходов эксперимента N(A) = 1 к
числу всех возможных исходов N = 10.
Ответ: 0,1
N ( A) 1
P ( A)
0,1
N
10

7.

Всего 150 возможных исходов.
Благоприятен исход, когда купленный фонарик окажется исправным.
Таких благоприятных исходов 150 – 3 = 147.
Находи вероятность,
как отношение благоприятных исходов 147 к числу всех возможных
исходов 150.
147/150 = 0,98
Ответ: 0,98

8. B10

При двукратном бросания игрального кубика может выпасть:
(5,1); (1,5); (2,4); (4,2); (3,3)
Итак : число всех возможных исходов -5
Число благоприятных исходов -2 :
1 бросок – выпало 1очко, или 1 бросок – выпал 2 очка.
Найдем отношение благоприятных исходов эксперимента 2
к числу всех возможных исходов 5
2
0,4
5
Ответ: 0,4

9.

Объемы подобных
многогранников
относятся
1
1
a 3 как кубы
V S Hлинейных
2 Sэлементов
H
S многогранников.
сходственных
3
3
4
2
осн
а
Н
а
осн
3
Итак : 2
а
а
осн
V
2
a
V V 3a
2
1a 3
H
3 4
1
3
2
2
1 3a2 3 a
1
V
3H
V S H
3
4
V 27a
3
От перестановки мест сомножителей
произведение не меняется.
3а
V 2 27 54
1 9a 3
1a 3
V
3H 9 3
H
3 4
3 4
2
2
осн
2
3
3
2
3а
3Н
2
2
2
2
3а
3а
V 27 2 54
2
Ответ: 54

10. B11

Объем цилиндра равен произведению площади основания на высоту: V = S осн⋅h
Т.к. при переливании объем воды не изменяется, то имеем: S осн⋅h=const.
Это значит, что Sоснования и высота связаны обратно пропорциональной зависимостью:
во сколько раз увеличивается площадь основания, во столько же раз
d
8d
384см
уменьшается высота воды в сосуде.
Основание цилиндра - круг,
площадь которого вычисляется:
S=π⋅r82 2
Если диаметр цилиндра
увеличился в 8 раз,
то и радиус увеличился в 8 раз.
Тогда площадь основания увеличилась в 64 раз.
Высота при этом уменьшилась в 64 раз и стала
Ответ: 6
384:64=6(см)

11. В11

1) Т.к. объем шара прямо пропорционален кубу радиуса,
V ( 2 R)
3
2
V R
то при увеличении радиуса в 2 раза объем шара увеличится
3
1
3
V
R
;
V 8R
3
R1
V
R
;
V (2 R)
R2
8V V
1
1
3
3
1
2
2 8
в 8 раз
3
2
2
Следовательно, вес шара тоже увеличится в 8 раз.
0,5⋅8=4
2) P=mg ; m=ρV ;
P pgV
4
V R ;
3
3
P
4
pg R ;
3
1
2
3
2
1
4
P 8 pg R
3
2
4
pg ( 2 R )
3
4
V R 0,5;
3
P
R 2R
3
1
3
1
3
От перестановки мест сомножителей
произведение не меняется
P 8 pg 0,5 4 pg
2
Ответ: 4

12. В11

В основании прямой призмы лежит квадрат со стороной
3. Боковые ребра равны 4 . Найдите объем цилиндра,
описанного около этой призмы.
3
3
R
Диагональ квадрата можно найти по теореме Пифагора:
d 3 3 27 3 2
2
4
2
d 3 2
2
2
Найдем площадь основания цилиндра
R
Sоснов = π·R2
3 2
;
S
2
2
3
3
осн
R
R
h
S
осн
9 2
4,5
4
4
V 4,5
Ответ: 18
4
18

13. В11

В конус, угол между образующей которого и основанием равен 60˚ ,
вписан шар. Найдите объем конуса, если объем шара равен 14.
S
V
4
3
= ·r
3
V 14
14;
7 27
3
4 R3 3 3
R
3
∆ АSB – равносторонний
14
; (SA=SB, ∟A=60˚) 2
3
27
SO – высота и медиана. Точка N – центр шара и точка
N
пересечения всех медиан в равносторонним треугольнике
АSВ
B
r
Точка N делит медиану SО в отношении 2:1 (считая от
вершины)
60˚
O
R
Итак NО = r = ⅓ SО, т.е. радиус вписанной окружности в
A
равносторонний треугольник равен ⅓ от высоты
треугольника
SO SA sin 600
SA SB AB 2 R.
АО = R , следовательно АВ = 2 R.
3
SO H 2 R
R 3;
2
1
1
3 RR 33
r SO 2 R
;
3
3
3
2 3
1
1
Vконуса R 2 R 3 R 3 3
3
3
3
1
Vконуса R 2 H
3
1 7 27 63
Vконуса
31,5
3 2
2
Ответ: 31,5