Управление колебаниями системы маятник-тележка с приводом методом скоростного биградиента

1. Управление колебаниями системы маятник-тележка с приводом методом скоростного биградиента

доцент каф. ЭИУ3-КФ КФ МГТУ им. Баумана Ю.И. Мышляев
ассистент, КФ МГТУ им. Н.Э. Баумана А.В. Финошин
Я.А. Долгов (студент гр.УТС.Б-51)
А.А. Зюзин (студент гр.УТС.Б-51)
Кафедра ЭИУ3-КФ
Работа выполнена при поддержке Российского фонда
фундаментальных исследований и Калужской
области Правительство (грант № 14-48-03115).

2. План

Введение и постановка задачи
Синтез алгоритма управления
Результаты моделирования
Вывод

3. Постановка задачи

æ M +m
ç
è - ml cos q
- ml cos q ö æ &
x&ö æ 0 mlq&sin q ö æ x&ö æ
0
ö æ 1ö
+
+
÷ ç &÷ ç
÷ ç
÷=ç ÷ f
2 ֍ &
&
I + ml ø è q ø è 0
0
ø è q ø è -mgl sin q ø è 0 ø
Подобный пример приведен статье MIT

4. Уравнение привода и ЦУ

Уравнение системы «тележка-маятник» в матричной форме:
&
&+ C (q, q&)q&+ j (q, q&) = Bf
H (q )q
динамика привода :
f&= u
ЦУ: раскачивание маятника с достижением колебаний
заданного уровня энергии:
E ® Ed
и стабилизация положения тележки
x ® 0, x&® 0

5. Методика синтеза

Система управления является двухкаскадной, а ЦУ зависит
от фазовых переменных выходного каскада, целесообразно
воспользоваться первым и третьим этапами метода
скоростного биградиента (МСБГ) . Т.к. по постановке задачи
параметры считаются заданными, отпадает необходимость
использования второго этапа МСБГ.
Этап 1. Управление механической подсистемой
Энергетический подход хорошо зарекомендовал себя в
задачах стабилизации неустойчивого положения равновесия
маятниковых систем
Этап 2. Управление приводом

6. Этап 1. Синтез виртуального управления выходным каскадом

7. Этап 1. Синтез виртуального управления выходным каскадом

Отклонение от желаемого уровня энергии
E%= E - Ed
Кандидат на функцию Ляпунова
1
V ( x ) = E%2
2
Производная функции Ляпунова в силу системы
V&= - K1E%2q&2 cos2 q £ 0, K1 > 0
С учетом ПД-регулятора
%&
&
&
x&
d = - K1 Eq cos q - k p x - k d x , k p > 0, k d > 0

8. Этап 2. Синтез алгоритма управления, обеспечивающего сходимость отклонения выхода привода от виртуального управления к нулю

дополнительная цель управления (ДЦУ)
f ® f virt
Уравнение гладкого управления, обеспечивающего достижение ДЦУ
u = -g ( f - f virt ) , g > 0

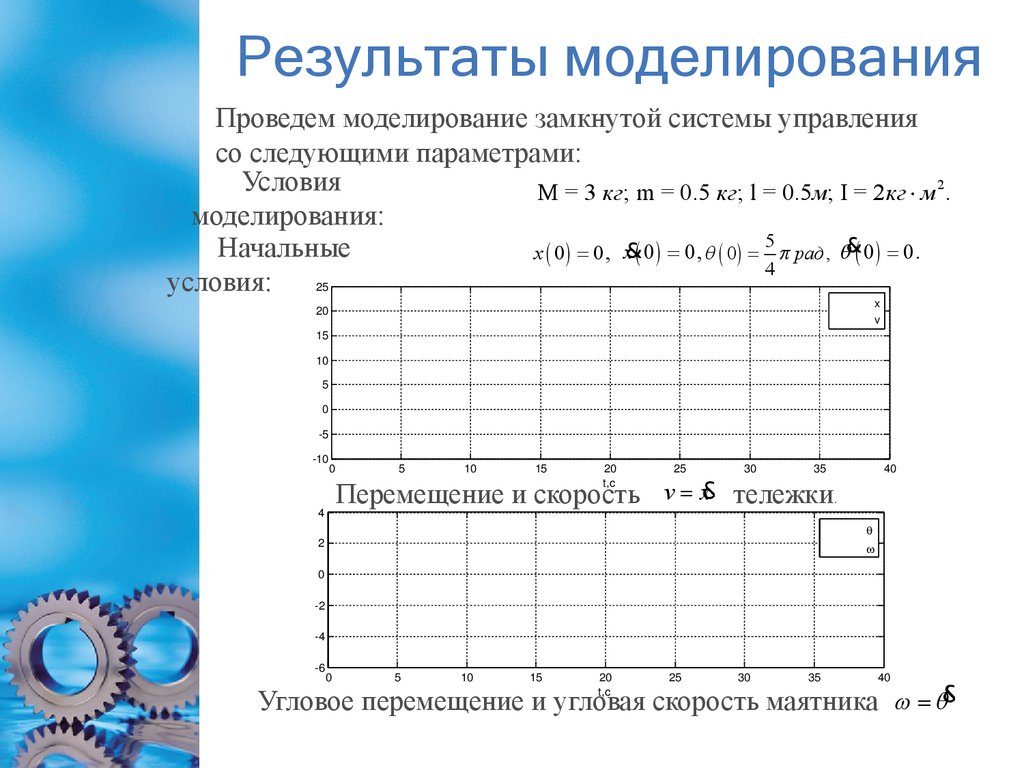
9. Результаты моделирования

Проведем моделирование замкнутой системы управления
со следующими параметрами:
Условия
M = 3 кг; m = 0.5 кг; l = 0.5м; I = 2кг × м 2 .
моделирования:
5
Начальные
x ( 0 ) = 0, x&( 0 ) = 0, q ( 0 ) = p рад , q&( 0 ) = 0.
4
условия:
25
 
x
v
20
15
10
5
0
­5
­10  
0
4
5
10
15
20
t,c
25
30
35
40
Перемещение и скорость v = x& тележки.
 
q
2
0
­2
­4
­6  
0
5
10
15
20
t,c
25
30
35
40
Угловое перемещение и угловая скорость маятника = q&

10. Результаты моделирования

150
 
f
100
50
0
­50  
0
5
10
15
20
t,c
25
30
35
40
Управляющая
сила.
600
400
 
u
200
0
­200
­400
­600
­800  
0
5
10
15
20
t,c
25
30
35
Управле
ние.
3
2
40
 
E
Ed
1
0
­1
­2  
0
5
10
15
20
t,c
25
30
35
40
Энергия маятника и желаемый уровень
энергии.

11. Вывод

Рассмотрена задача стабилизации неустойчивого
положения тележки с маятником, управляемой приводом.
Синтезирован алгоритм управления первым и третьим
этапами метода скоростного биградиента (МСБГ).
Проведено моделирование, подтверждающее достижение
заданного качества.

12.

Спасибо за
внимание