Урок № 3. Метод координат в пространстве. Декартовы координаты в пространстве

1.

Урок № 3
МЕТОД КООРДИНАТ В
ПРОСТРАНСТВЕ
Декартовы координаты в пространстве
Ренее Декаерт, французский философ, математик, механик, физик и физиолог
Высь, ширь, глубь.
Лишь три координаты.
Мимо них где путь? Засов закрыт.
С Пифагором слушай сфер сонаты,
Атомам дли счёт, как Демокрит.
В. Брюсов.

2.

План урока
1 Введение прямоугольной системы координат в пространстве.
2 Расположение точек в системе координат.
3 Нахождение координат точек в пространстве.
4 Построение точки в пространстве по её координатам.
5 Понятие радиус-вектора.
6 Разложение вектора по координатным векторам.
7 Нахождение координат вектора суммы векторов, вектора
разности векторов, вектора умноженного на данное число.
8 Решение задач.
9 Запись ДЗ.

3.

МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
Система координат на плоскости
Y
y
Система координат в пространстве
Z
z
M(x;y)
абсцисса
ордината
О
x
1) 2 прямые
2) Точка – НК
3) Направление осей
4) Название осей
5) Точка М
6) Название
координат
точки М
X
X
1)
2)
3)
4)
x
аппликата
y
Y
Ось абсцисс
Ось ординат
Ось аппликат
OX; OY; OZ
5) Координатные плоскости
6) Точка М
7) Название
координат
точки М
ордината
M(x;y;z)
О
3 прямые
Точка – НК
Направление осей
Название осей
абсцисса
XOY; XOZ; YOZ

4.

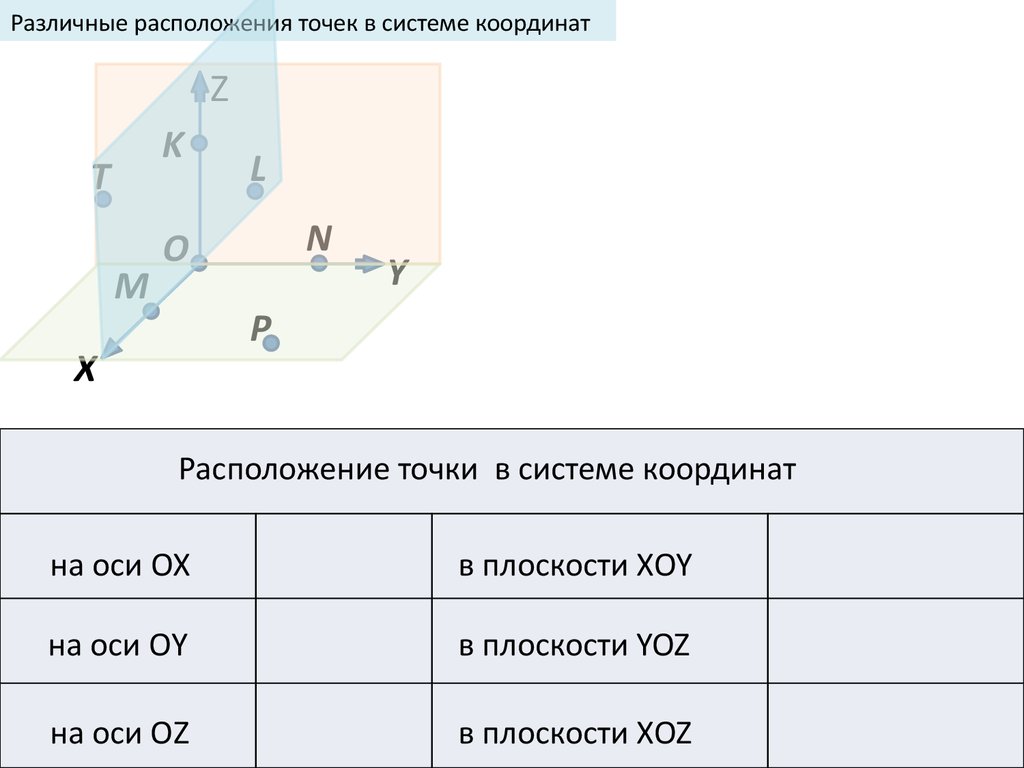
Различные расположения точек в системе координат
Z
K
T
M
L
N
О
Y
P
X
Расположение точки в системе координат
на оси ОХ
в плоскости ХOY
на оси ОY
в плоскости YOZ
на оси ОZ
в плоскости ХOZ

5.

1) Нахождение координат точек
2) Нахождение координат точек
Дан куб с длиной ребра 2
Z
C1
B1
A1
A
2
D1
B
Y
Дан прямоугольный параллелепипед
с измерениями 2; 5; 7
2
X
Z
B1
A1
C
D
2
Найдите координаты всех вершин куба
A
X
D1
5
2
B
7
C
D
Найдите координаты всех вершин
прямоугольного параллелепипеда
3) Построение точки по её координатам
Постройте точки в прямоугольной
системе координат:
М(3; 4; 5) и Т(-2; 5; -7)
C1
Y

6.

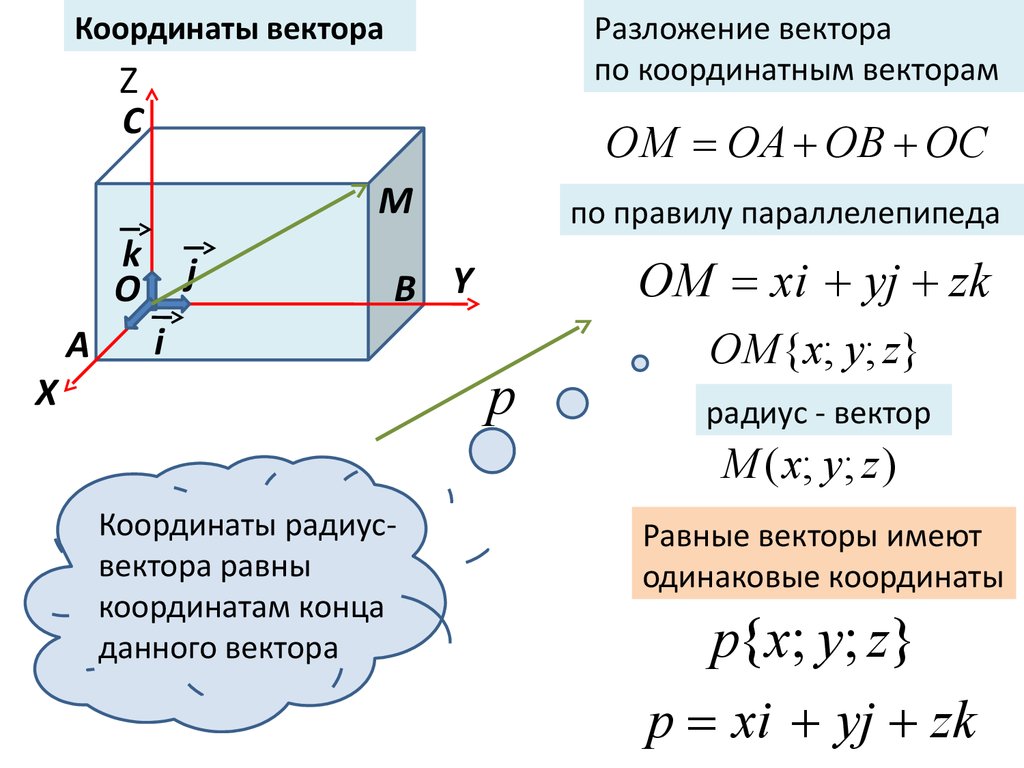
Координаты вектора
Разложение вектора
по координатным векторам
Z
С
ОМ ОА ОВ ОС
М
k
О
X
А
j
по правилу параллелепипеда
ОМ xi yj zk
В Y
i
р
ОМ {x; y; z}
радиус - вектор
М ( x; y; z )
Координаты радиусвектора равны
координатам конца
данного вектора
Равные векторы имеют
одинаковые координаты
р{x; y; z}
р xi yj zk

7.

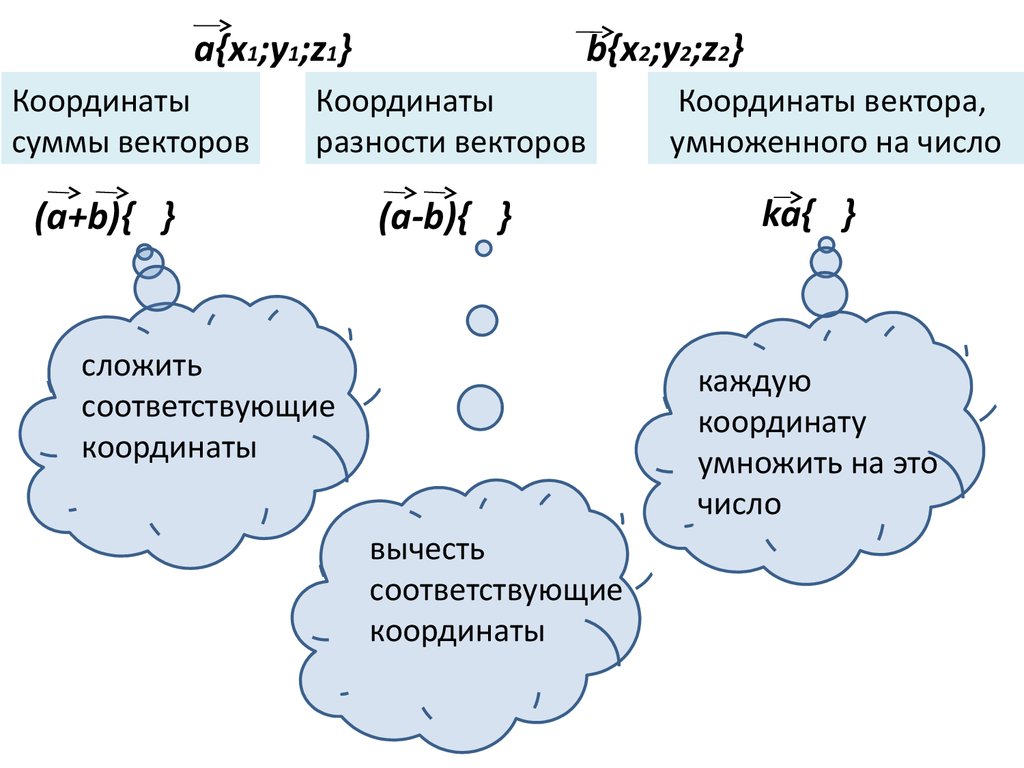
a{x1;y1;z1}
Координаты
суммы векторов
b{x2;y2;z2}
Координаты
разности векторов
(a+b){ }
(a-b){ }
сложить
соответствующие
координаты
Координаты вектора,
умноженного на число
ka{ }
каждую
координату
умножить на это
число
вычесть
соответствующие
координаты

8.

4) Дано разложение вектора по единичным векторам, запишите координаты вектора.
р 3i 2 j k , р j 6k , р k .
5) Даны координаты вектора, запишите разложение вектора по единичным векторам.
р{ 3;6;1}, р{ 2;5;0}, р{0; 1;0}.

9.

Домашнее задание с урока 3:
п.46, 47 и конспект, уметь составить грамотный рассказ,
№ 400, 402, 403, 404, 410
на следующем уроке простейшая СР