Отражение и прохождение волны на границе двух сред. Колебания и волны. 13

1. Раздел курса «Колебания и волны»

Тема
Отражение и прохождение
волны на границе двух сред

2. Рассмотрим струну, состоящую из двух полубесконечных частей с волновыми со -противлениями Z1 и Z2. Части соединены в точке x =

Рассмотрим струну, состоящую из двух
полубесконечных частей с волновыми со противлениями Z1 и Z2. Части соединены в
точке x = 0.
Силу натяжения всей струны обозначим Т0.

3.

Поставим задачу: выяснить как влияют
волновые сопротивления Z1 и Z2 на ампли туды и фазы отраженной и прошедшей
волны.

4.

Воспользуемся для упрощения матема тических выкладок комплексным представлением волновых уравнений.
Пусть начальная фаза источника φ =0.
Тогда для волны, падающей на границу
двух сред, получим
пад А1 cos t k1x А1e
Здесь
i 1
i t k1x

5.

Для волны, отраженной от границы
сред, и волны, прошедшей через
границу, получаем
i t k1x
отр В1 cos t k1x В1e
i t k2 x
прош А2 cos t k2 x А2e

6.

На границе сред в точке с координа той x = 0 (см. рис.) должны выпол –
няться граничные условия
0 0
x 0
x 0

7. Основные понятия

• Величина, равная отношению ампли туды отраженной волны В1 к амплитуде
падающей волны А1 называется ампли тудным коэффициентом отражения R:
B1
R .
A1

8.

Основные понятия
•Величина, равная отношению амплитуды
прошедшей волны А2 к амплитуде пада ющей волны А1 называется амплитудным
коэффициентом прохождения D:
A2
D
.
A1

9. Итак, доказано, что связь коэффициента отражения R с волновыми сопротивлениями граничащих сред Z1 и Z2 имеет вид

Z1 Z 2
R
.
Z1 Z 2

10.

При этом, если Z1 < Z2, то фаза отраженной
волны в точке отражения (на границе сред)
скачком изменяется на радиан по отношению
к фазе падающей волны.
Если же Z1 > Z2, то фаза отраженной волны в
точке отражения совпадает с фазой падающей
волны.
отр , при Z1 Z 2 ;
отр 0, при Z1 Z 2 .

11. Кроме того, доказано, что связь коэффициента прохождения D с волновыми сопротивлениями граничащих сред Z1 и Z2 имеет вид

2Z1
D
.
Z1 Z 2
При этом фаза прошедшей волны в точке
прохождения (на границе сред) всегда совпадает
с фазой падающей волны:
прош 0 как при Z1 Z 2 , так и при Z1 Z 2 .

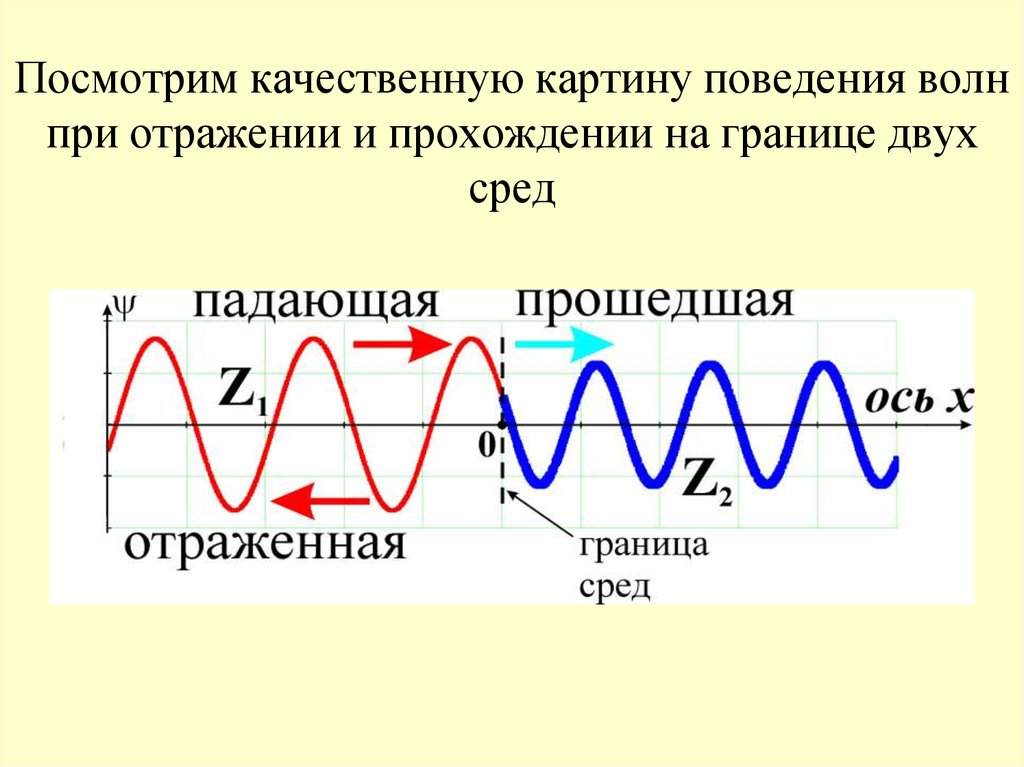
12. Посмотрим качественную картину поведения волн при отражении и прохождении на границе двух сред

13. Рассмотрим два важных частных случая. 1). Пусть Z2  . Тогда коэффициент прохождения

Рассмотрим два важных частных случая.
1). Пусть Z2 .
Тогда коэффициент прохождения
A2
2Z1
2Z1
D
0
A1 Z1 Z 2
Z1
Это означает, что волна не распространяется во
второй среде.
.

14.

Коэффициент отражения при этом равен
Z1
1
B1 Z1 Z 2
Z2
R
1
Z1
A1 Z1 Z 2
1
Z2
Это означает, что амплитуда отраженной и
падающей волны одинаковы. А знак минус
указывает, как отмечалось выше, что
отр , при Z1 Z 2 .

15. 2). Пусть Z2  0. Тогда коэффициент прохождения

2). Пусть Z2 0.
Тогда коэффициент прохождения
A2
2Z1
2Z1
D
2.
A1 Z1 Z 2
Z1 0
Это означает, что амплитуда прошедшей
волны вдвое больше, чем амплитуда
падающей.

16.

Коэффициент отражения при этом равен
B1
R
A1
Z1 Z 2 Z1 0
1.
Z1 Z 2 Z1 0
Это означает, что амплитуды отраженной и
падающей волны и в этом случае одинаковы. А
знак плюс указывает, что скачка фазы при
отражении волны не происходит.