Оценка одновременно нескольких параметров

1. Потенциальная точность совместной оценки нескольких параметров

2.

Функция правдоподобия нескольких параметров:
1 T
2
P y t / Q1 ,Q 2 , … ,Q n k1 exp
[ y (t ) s (t ; Q1 ,Q 2 , … ,Q n )] dt
N
0 0
1
k1 exp
N 0
T
0
2
y 2 t dt
N0
T
0
1
y t s t ; Q1 ,Q 2 , … ,Q n dt
N0
1
k1 exp
N 0
2
k2 exp
N
0
y t s t ; Q1 ,Q 2 , … ,Q n dt ,
T
0
T
0
1
y 2 t dt
N0
2
2
s t ; Q1 ,Q 2 , … ,Q n dt exp
N 0
0
T
s t ; Q1 ,Q 2 , … ,Q n dt
0
T
T
0
2
y t s t ; Q1 ,Q 2 , … ,Q n dt
где входная реализация y(t ) s(t;Q10 ,Q20 ,…Qn0 ) n(t )
2 T
P y (t ) / Q1 ,Q2 , …,Q n k2 exp
[ s(t; Q10 ,Q 20 , …,Q n0 ) n(t )] s(t; Q1 ,Q 2 , …,Q n ) dt
N 0 0

3.

Оценку проводим по максимуму ФП при отношении с/ш >> 1
Раскладываем логарифм ФП в ряд Тейлора для истинных значений параметров:
ln P y (t ) / Q1 ,Q 2 , … ,Q n ln P y (t ) / Q10 ,Q 20 , … ,Q n0
n
i 1
1
2
Q =Q
ln P y (t ) / Q1 ,Q 2 , … ,Q n Q12 =Q1020 Q i Q i 0
Qi
Q n =Q n0
n
n
i 1
k 1
2
Q =Q
ln P y (t ) / Q1 ,Q 2 , … ,Q n Q12 =Q1020 Q i Q i 0 Q k Q k 0
Qi Q k
Q n =Q n0

4.

Матрица, составленная из средних значений вторых производных
Aik
2
Q1 =Q10
ln P y (t ) / Q1 ,Q 2 , … ,Q n Q2 =Q20
Qi Q k
Q n =Q n0
называется информационной матрицей Фишера и характеризует
«остроту» многомерного пика ФП.

5.

Матрица вторых моментов погрешностей оценок ik , характеризующая
предельную точность измерения параметров, вычисляется путем обращения
информационной матрицы Фишера: ik Aik
1
.
Другими словами, обратная матрица ik состоит из средних вторых
моментов минимальных ошибок измерения параметров, достижимых в
случае соместно эффективных оценок.
Важно, что если кодировки отдельных параметров в сигнале y(t) независимы,
то ik - диагональная матрица с элементами Qi2 , равными дисперсии
минимально достижимых ошибок измерения отдельных параметров.

6.

Рассмотрим случай одновременной оценки двух параметров
2ЭС
P y (t ) / Q1 ,Q 2 k2 exp
Q1 ,Q 2
N0
Q1 ,Q 2 С Ш ,
где
s t ; Q10 ,Q 20 s t ; Q1 ,Q 2 dt
Q ,Q
,
С
1
2
2ЭС
n t s t ; Q1 ,Q 2 dt
Ш Q1 ,Q 2
.
2ЭС

7.

Раскладываем АКФ в ряд в точке истинного значения параметра:
Q1 ,Q 2 Q10 ,Q 20
Q1 ,Q 2
Q1
Q1 Q10
Q2 Q20
Q1 Q10
Q1 ,Q 2
Q 2
Q1 Q10
Q2 Q20
Q2 Q20
2
2 Q1 ,Q 2
1 Q1 ,Q 2
2
Q1 Q10
Q1 Q10 Q2 Q20
2
Q1 Q10
2
Q1 Q 2 Q1 Q10
Q1
Q2 Q20
Q2 Q20
2 Q1 ,Q 2
Q 2 Q1
Q1 Q10
Q2 Q20
Q2 Q20 Q1 Q10
2 Q1 ,Q 2
Q 2 2
Q1 Q10
Q2 Q20
Q2 Q20
2
Получаем выражение, позволяющее определить элементы матрицы Aik :
2
2
2ЭС 1 Q1 ,Q 2
P y (t ) / Q1 ,Q 2 k3 exp
Q
Q
1
10
2
Q1 Q10
Q1
N0 2
Q2 Q20
2
2 Q1 ,Q 2
Q1 Q 2
Q1 Q10
Q2 Q20
Q1 Q10 Q2 Q20
2 Q1 ,Q 2
Q 2 2
Q1 Q10
Q2 Q20
Q 2 Q 20
2

8.

A
2
Q12
2
Q1 Q 2
2
Q 2 Q1
2
Q 2 2
Находим элементы обратной матрицы, характеризующие минимальные
ошибки соместных измерений:
A11
1
A
A21
где Aik 1
A12
,
A22
i k
M ik алгебраическое дополнение,
а M ik минор матрицы A .

9.

Таким образом из матрицы
A
2
Q12
2
Q1 Q 2
2
Q 2 Q1
2
Q 2 2
получаем обратную ей матрицу
2
Q 2 2
1
A
2
Q1 Q 2
где определитель
2
Q 2 Q1
,
2
Q12
2
2 2 2
2 2
2
1
r
Q1Q2
Q12 Q 2 2 Q1 Q 2
Q12 Q 2 2

10.

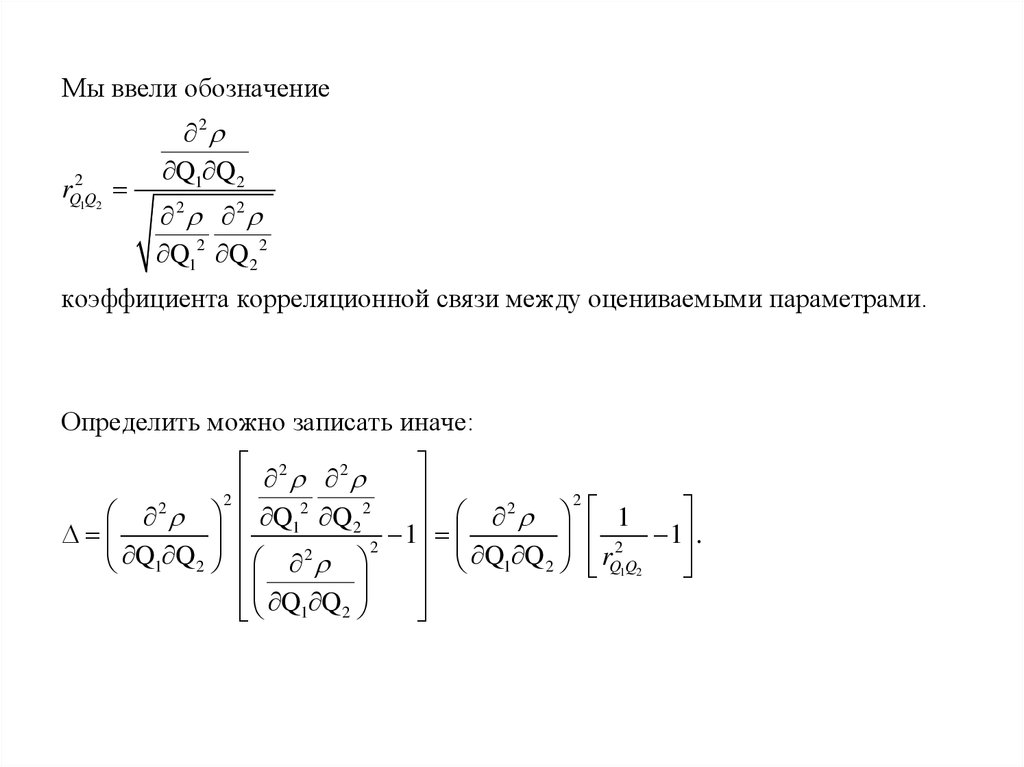
Мы ввели обозначение
rQ21Q2
2
Q1 Q 2
2 2
Q12 Q 2 2
коэффициента корреляционной связи между оцениваемыми параметрами.
Определить можно записать иначе:
2 2
2
2
2
2
2
2
1
Q1 Q 2
1
2 1 .
2
2
Q Q
r
Q1 Q 2
1 2 Q1Q2
Q1 Q 2

11.

Запишем обратную матрицу в виде
1
1
A
2
2
1
r
Q1Q2
2
Q1
rQ21Q2
2
1 rQ21Q2
Q1 Q 2
rQ21Q2
1
2
1 rQ21Q2
Q1 Q 2
2
2
1
r
Q1Q2
2
Q 2
Окончательно получаем:
Q2
1
1
;
2
2ЭС Q1 ,Q 2
2
1
r
Q1Q2
2
Q1 Q10
N0
Q1
Q2 Q20
Q2
2
1
.
2
2ЭС Q1 ,Q 2
2
1
r
Q1Q2
2
Q1 Q10
N0
Q 2
Q2 Q20

12.

Множитель
1
отражает корреляционную связь между
1 r
измеряемыми параметрами.
2
Q1Q2
При наличии корреляции (r 0) этот множитель больше единицы
и точность хуже, чем при некоррелированных параметрах Q1 и Q 2 .