Похожие презентации:
Решение тригонометрических неравенств
1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ.
Ионова Елена Владимировнаучитель первой категории
ГБОУ СОШ № 267 СВАО г.Москвы.
2013г.
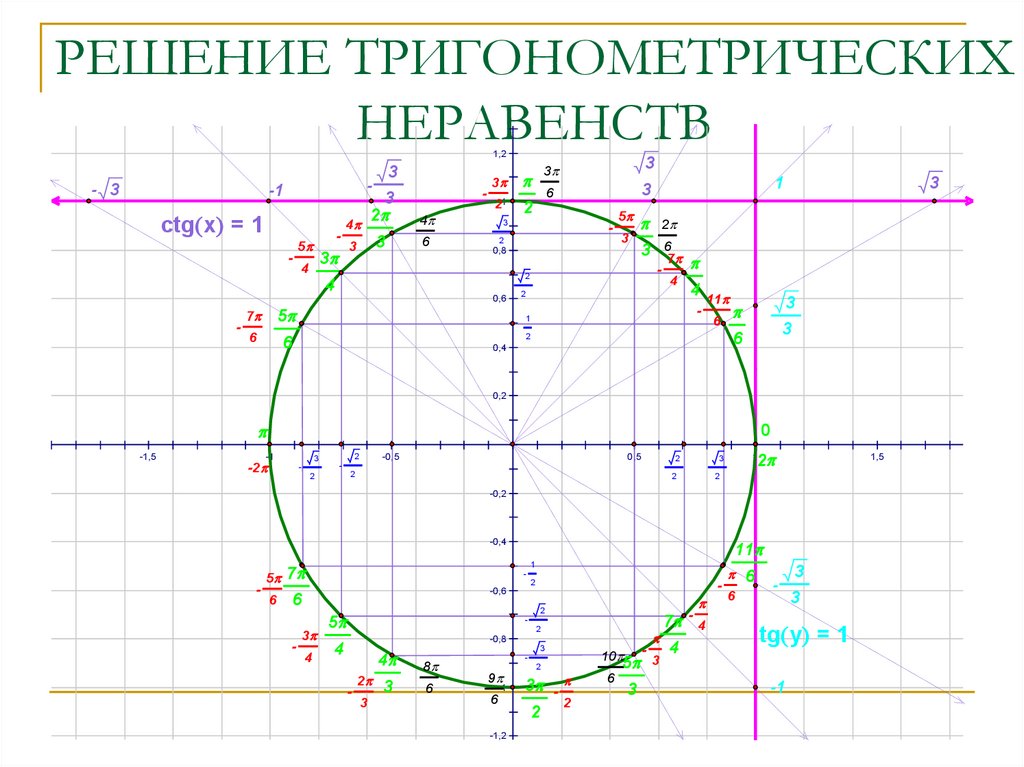
2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ
1,2- 3
-
-1
ctg x = 1
-
-
5
4
3
4
3
-
3
2
4
3
6
3
3
21
2
-
5
6
6
3
6
3
3
-
2
5
3
2
3
6
7
-
2
0,6
1
0,8
4
7
3
4
2
3
4
-
1
11
6
3
3
6
2
0,4
0,2
-1,5
0
-1
3
-2
-
2
-0,5
0,5
2
2
2
2
1
3
2
1,5
2
-0,2
11
-0,4
-
5
6
7
1
-
6
-
2
-0,6
3
4
2
5
2
-0,8
4
4
-
2
3
3
3
8
6
10
-
9
-1
6
-1,2
2
3
2
-
2
5
6
3
-
3
7
4
-
4
6
6
-
3
3
tg y = 1
-1
3. РЕШИМ УРАВНЕНИЕ:
2COSХ
2
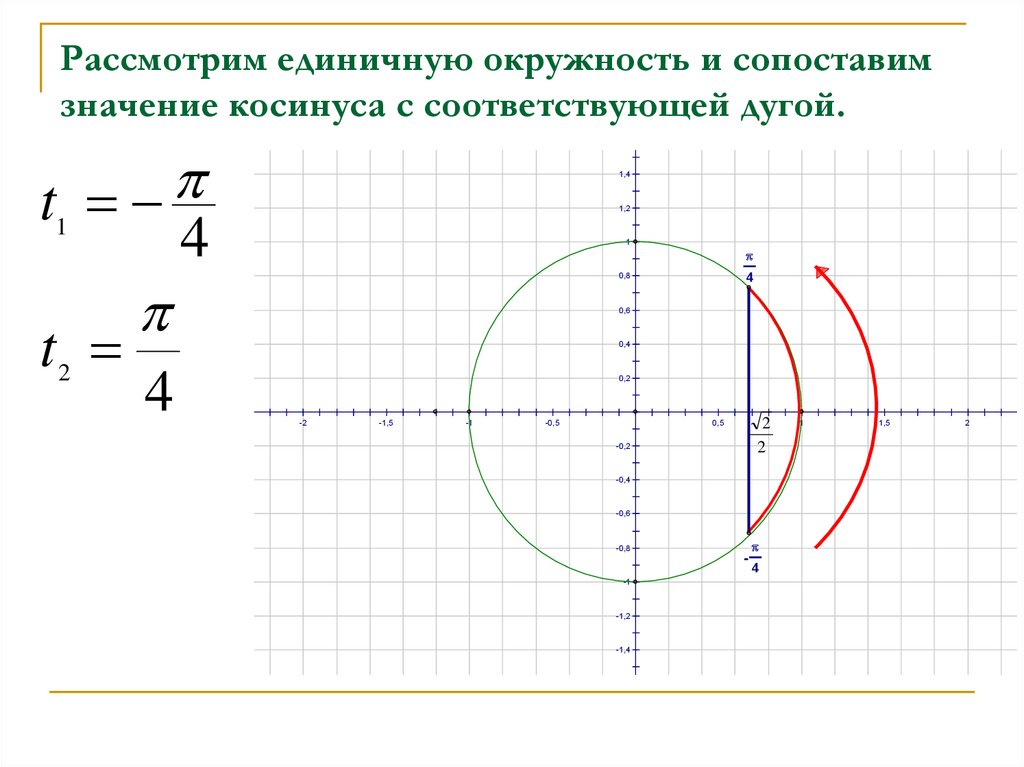
4. Рассмотрим единичную окружность и сопоставим значение косинуса с соответствующей дугой.
t1
t2
4
1,4
1,2
4
1
4
0,8
0,6
0,4
0,2
-2
-1,5
-1
-0,5
2
2
0,5
-0,2
-0,4
-0,6
-0,8
-1
-1,2
-1,4
4
1
1,5
2
5. Рассмотрим график функции
y cos xОтметим значение функции и соответствующее ему значение аргумента
3
2,5
2
1,5
1
0,5
2
2
-5
-4
-3
-2
-1
4
4
-0,5
1
2
-1
-1,5
-2
-2,5
t
,t
1
4
2
4
3
4
5
6.
4Период косинуса
равен 2π, а
значит точки t1 и
t2 будут
повторяться
через каждые
2π.
t1+2πn и t2+2πn,
nЄZ
Решение
данного
неравенства
имеет
следующий вид:
2 n x
4
2 n, n
7. РЕШИ САМОСТОЯТЕЛЬНО:
11) cos x ;
2
3
2) cos( x )
;
3
2
3) cos( 2 x ) 0.
4
8. ПРОВЕРЬ СВОЙ ОТВЕТ:
51) 2 n x
2 n, n ;
3
3
7
2)
2 n x 2 n, n ;
6
2
3
7
3)
n x
n, n .
8
8






 Математика
Математика








