Начертательная геометрия. Лекция 3

1. Лекция 3

• Взаимное расположение плоскостей.
• Взаимное расположение прямой и
плоскости.

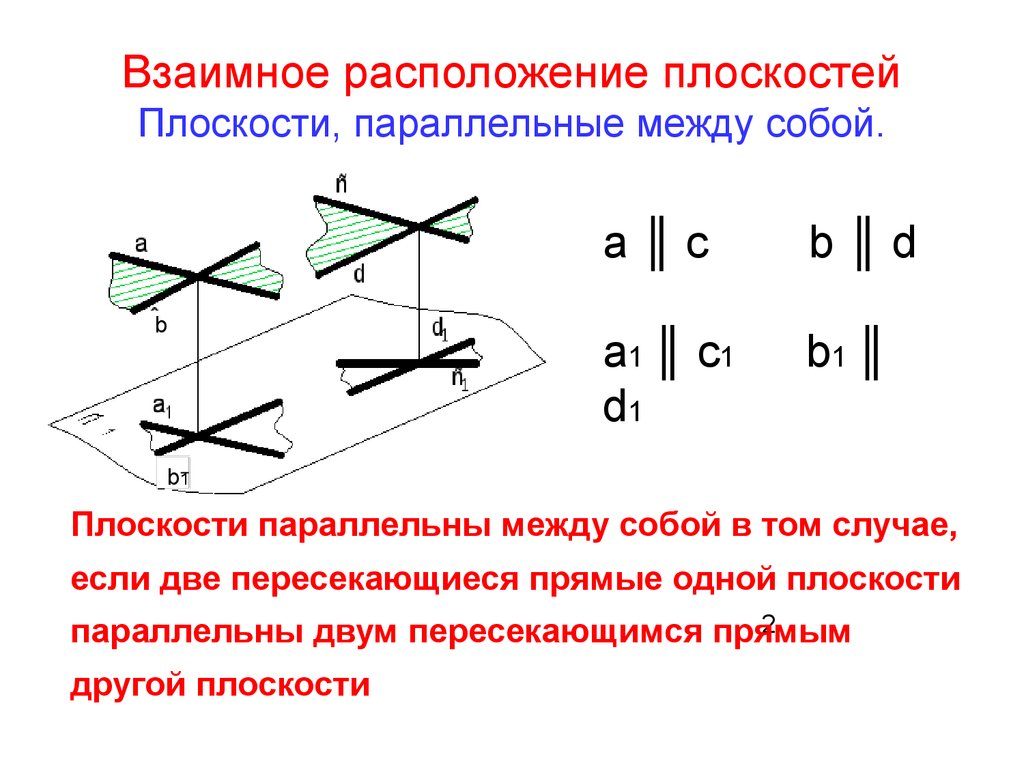
2. Взаимное расположение плоскостей Плоскости, параллельные между собой.

b
a║c
b║d
a1 ║ c 1
d1
b1 ║
b1
Плоскости параллельны между собой в том случае,
если две пересекающиеся прямые одной плоскости
2
параллельны двум пересекающимся прямым
другой плоскости

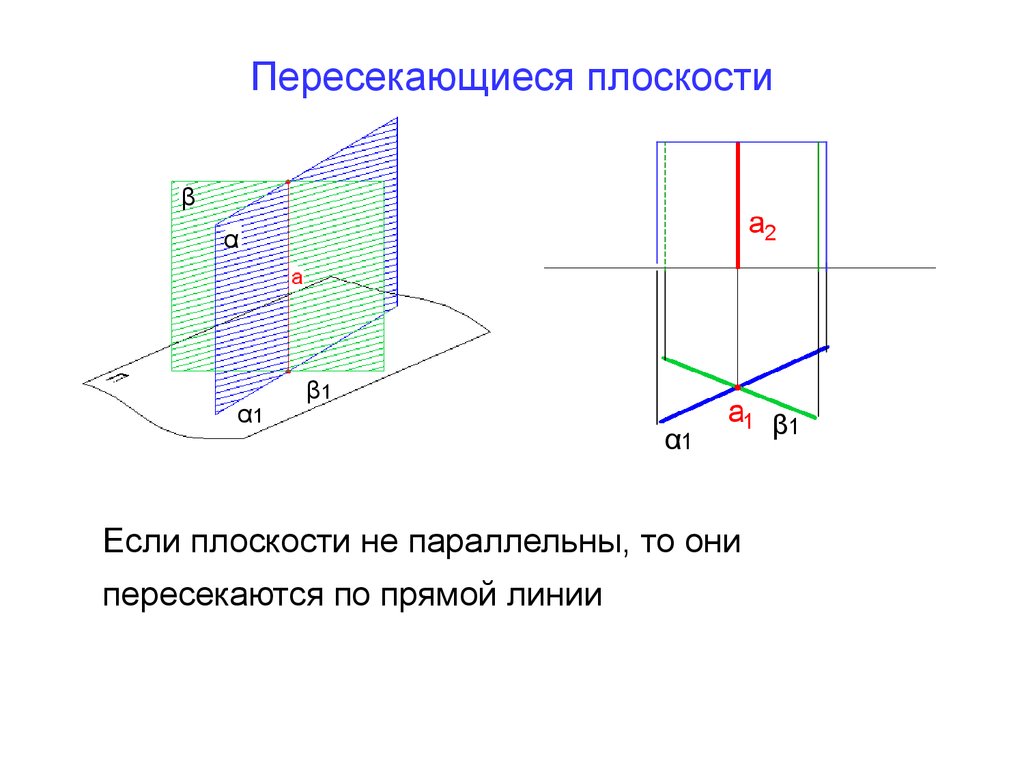
3. Пересекающиеся плоскости

β
α
α1
β1
α1
Если плоскости не параллельны, то они
пересекаются по прямой линии
β1

4.

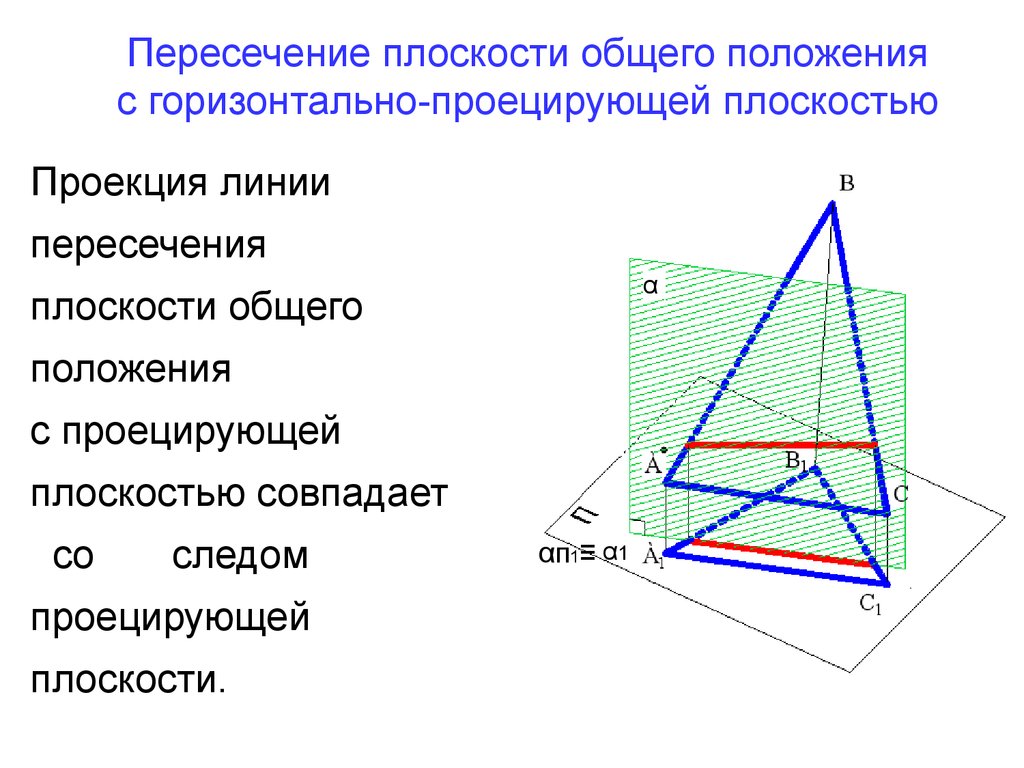
Пересечение плоскости общего положения
с горизонтально-проецирующей плоскостью
Проекция линии
пересечения
α
плоскости общего
положения
с проецирующей
плоскостью совпадает
со
следом
проецирующей
плоскости.
αп1≡ α1

5.

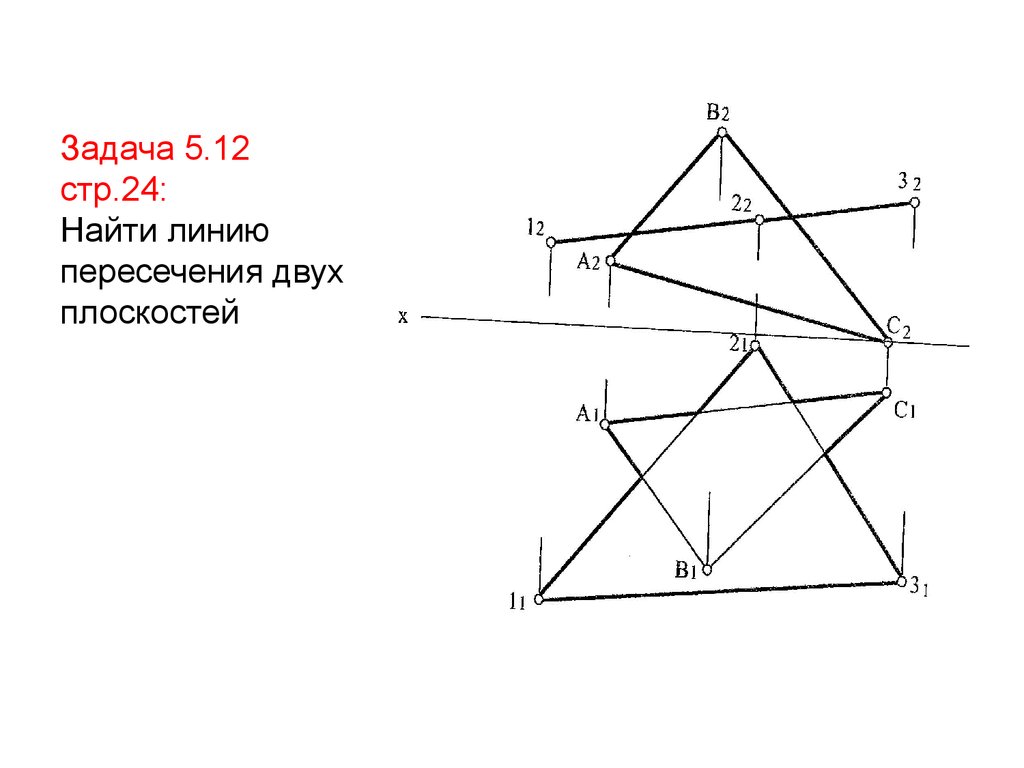
Задача 5.12
стр.24:
Найти линию
пересечения двух
плоскостей

6.

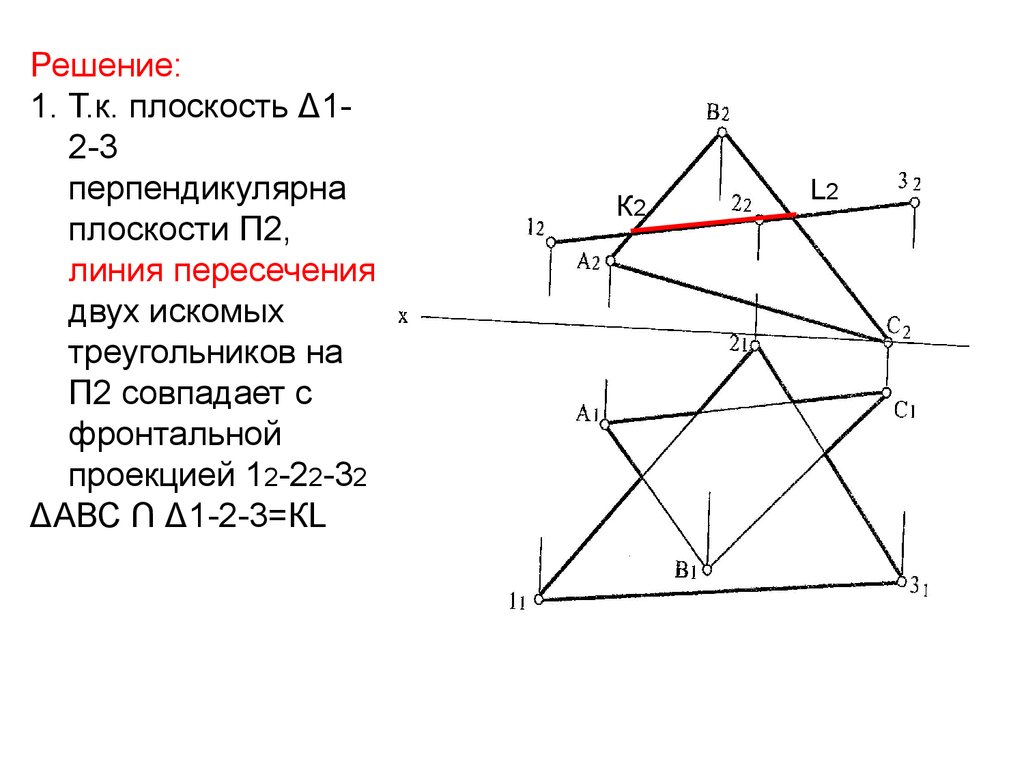
Решение:
1. Т.к. плоскость Δ12-3
перпендикулярна
плоскости П2,
линия пересечения
двух искомых
треугольников на
П2 совпадает с
фронтальной
проекцией 12-22-32
ΔАВС ∩ Δ1-2-3=КL
К2
L2

7.

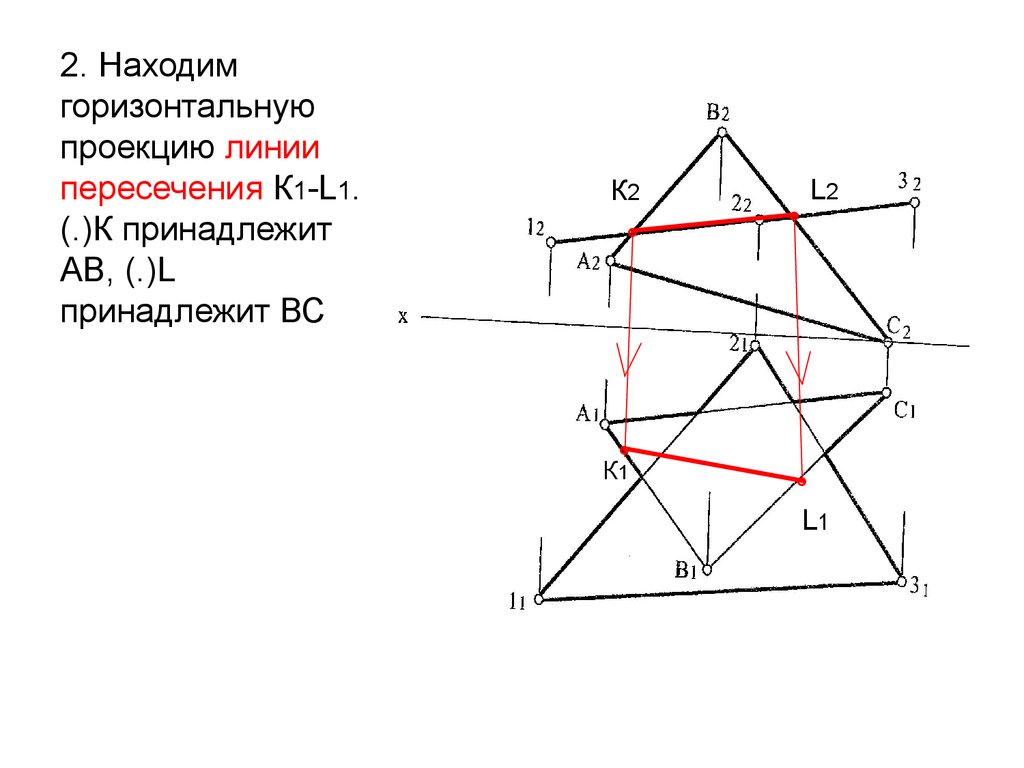
2. Находим
горизонтальную
проекцию линии
пересечения К1-L1.
(.)К принадлежит
АВ, (.)L
принадлежит ВС
L2
К2
°
°
К1
°
°
L1

8.

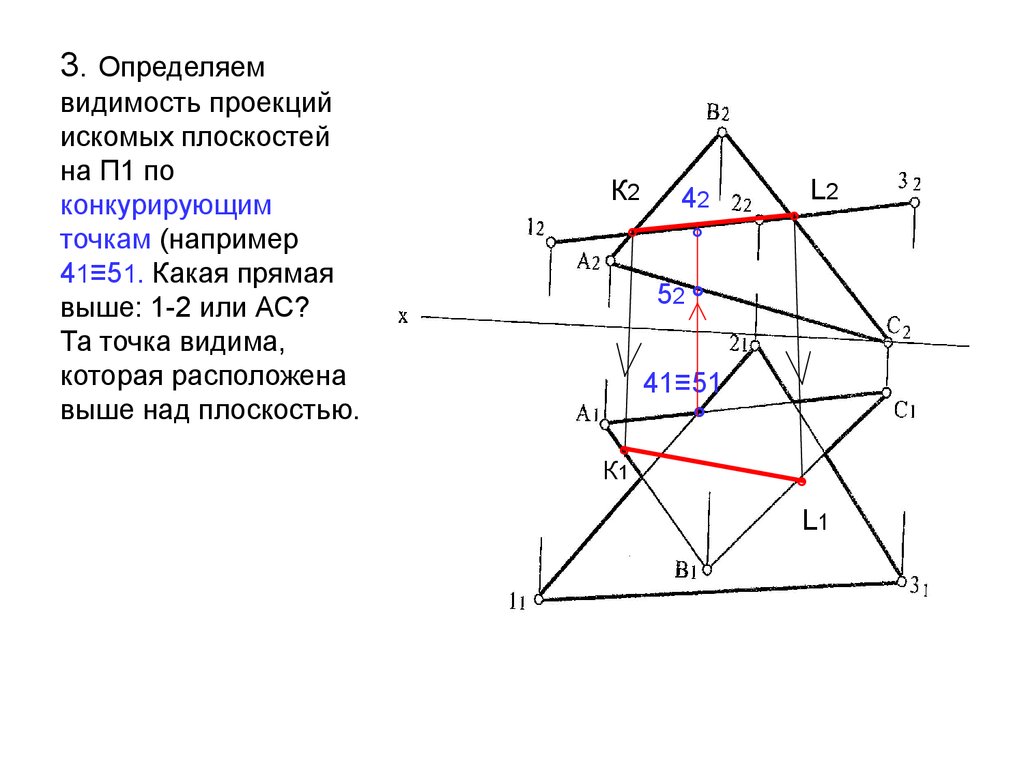
3. Определяем
видимость проекций
искомых плоскостей
на П1 по
конкурирующим
точкам (например
41≡51. Какая прямая
выше: 1-2 или АС?
Та точка видима,
которая расположена
выше над плоскостью.
К2
°
42
°
L2
°
52 °
41≡51
°
°
К1
°
L1

9.

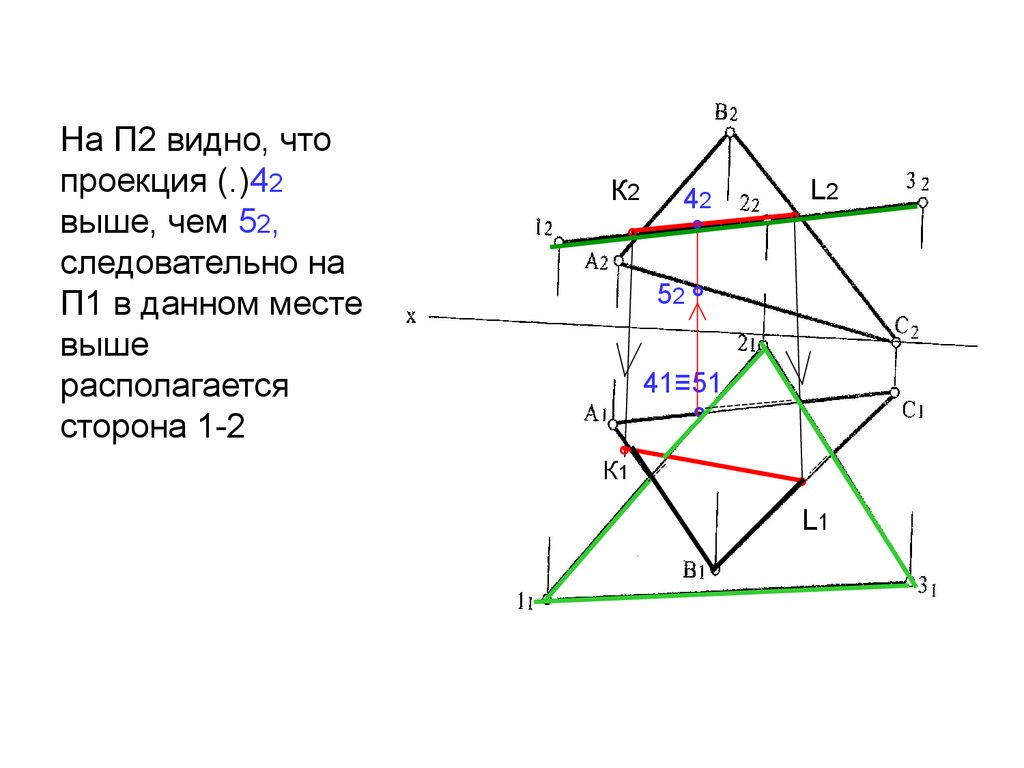
На П2 видно, что
проекция (.)42
выше, чем 52,
следовательно на
П1 в данном месте
выше
располагается
сторона 1-2
К2
°
42
°
L2
°
52 °
41≡51
°
°
К1
°
L1

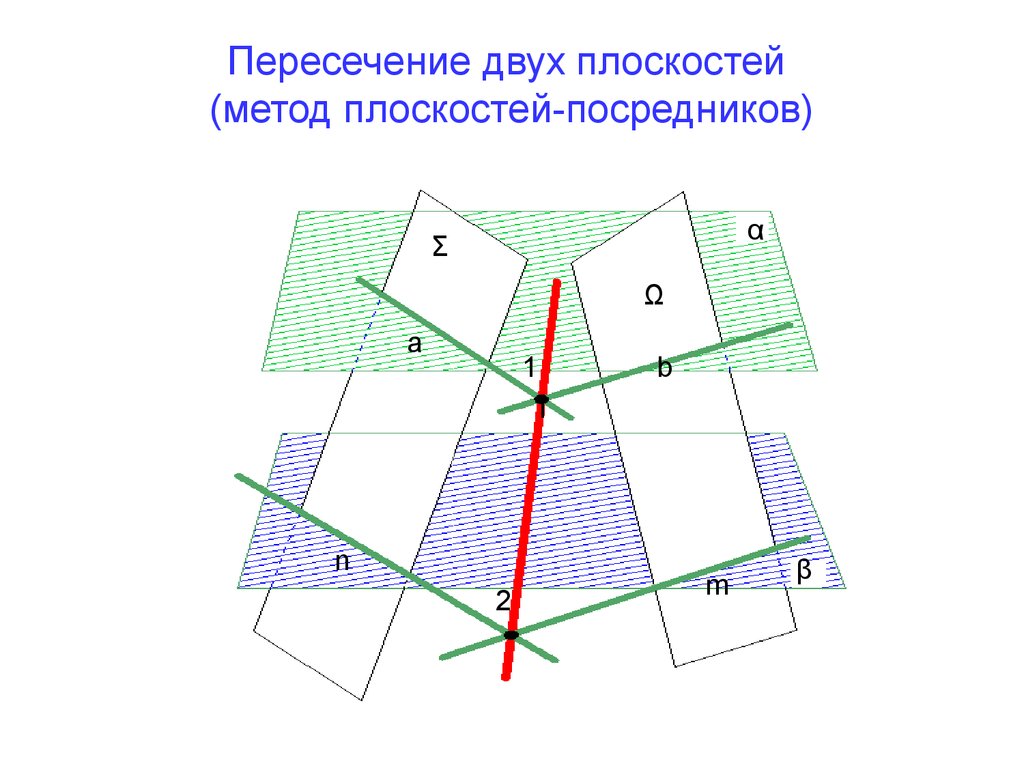
10. Пересечение двух плоскостей (метод плоскостей-посредников)

α
Σ
Ω
a
1
b
I
n
2
m
β

11. Алгоритм решения задачи: пересечение двух плоскостей

1. Рассекаем две заданные плоскости Σ и Ω вспомогательной плоскостьюпосредником α.
2. Строим линии пересечения вспомогательной плоскости α с заданными Σ и Ω
(Σ∩ α=a,
Ω ∩ α=b ).
3. Находим точку пересечения полученных линий (·) 1→ (a ∩ b =1).
4. Рассекаем заданные плоскости второй вспомогательной плоскостьюпосредником β.
5. Строим линии пересечения вспомогательной плоскости β с заданными Σ и Ω
(Σ∩ β =n,
Ω ∩ β =m ).
6. Находим точку пересечения полученных линий (·)2 (n ∩ m =2)
7. Соединяем точки I и 2, получаем линию пересечения искомых плоскостей Σ
иΩ.

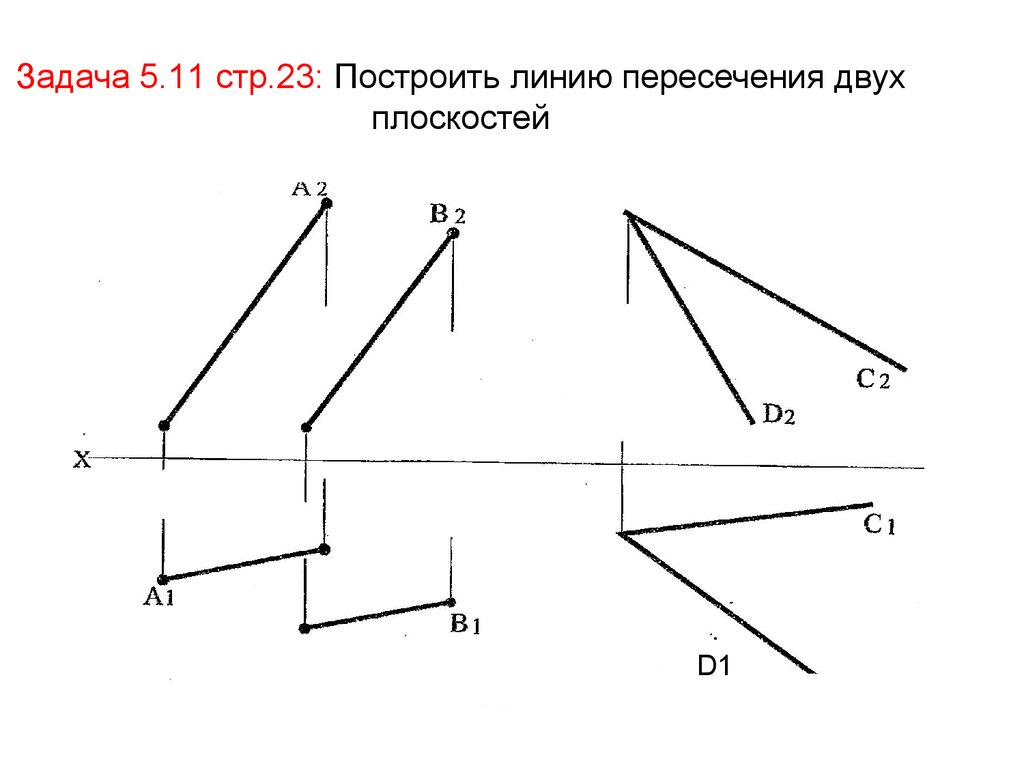
12. Задача 5.11 стр.23: Построить линию пересечения двух плоскостей

D1

13.

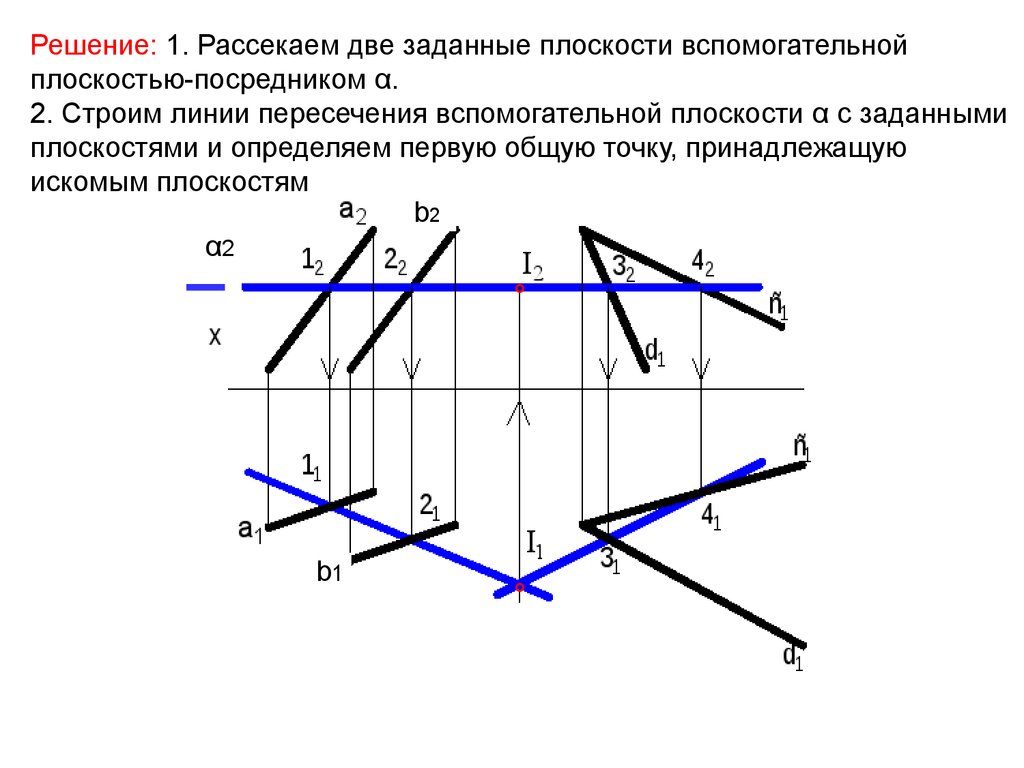
Решение: 1. Рассекаем две заданные плоскости вспомогательной
плоскостью-посредником α.
2. Строим линии пересечения вспомогательной плоскости α с заданными
плоскостями и определяем первую общую точку, принадлежащую
искомым плоскостям
b2
α2
°
b1
°

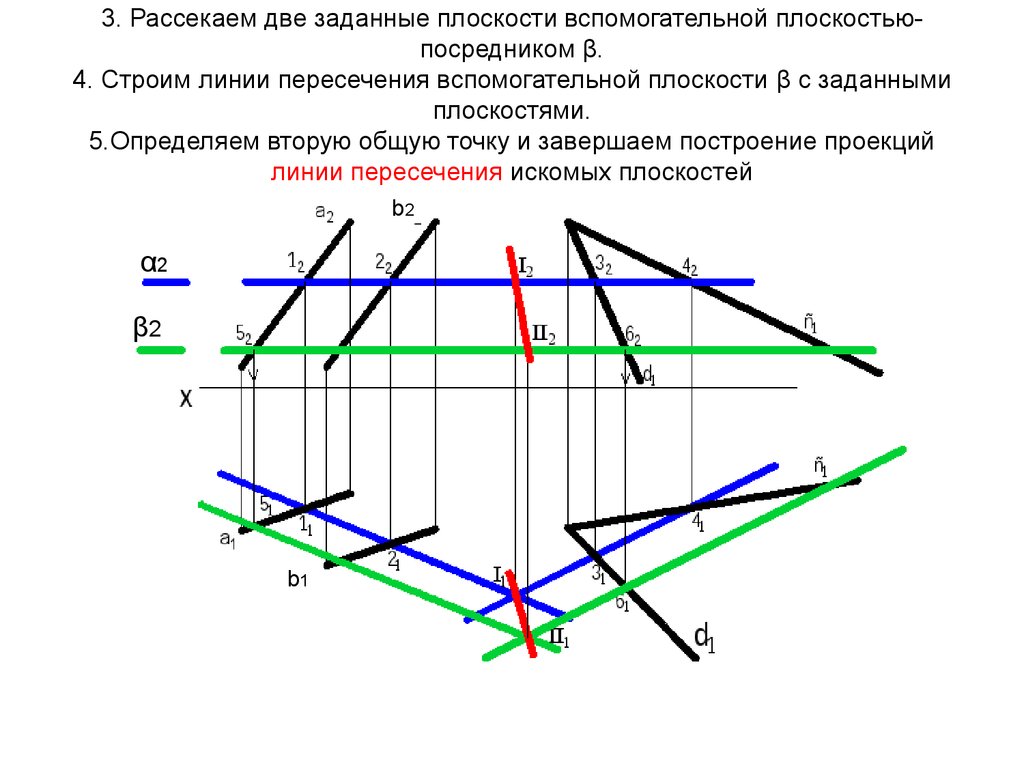
14. 3. Рассекаем две заданные плоскости вспомогательной плоскостью-посредником β. 4. Строим линии пересечения вспомогательной плоскости β с за

3. Рассекаем две заданные плоскости вспомогательной плоскостьюпосредником β.
4. Строим линии пересечения вспомогательной плоскости β с заданными
плоскостями.
5.Определяем вторую общую точку и завершаем построение проекций
линии пересечения искомых плоскостей
b2
α2
β2
b1

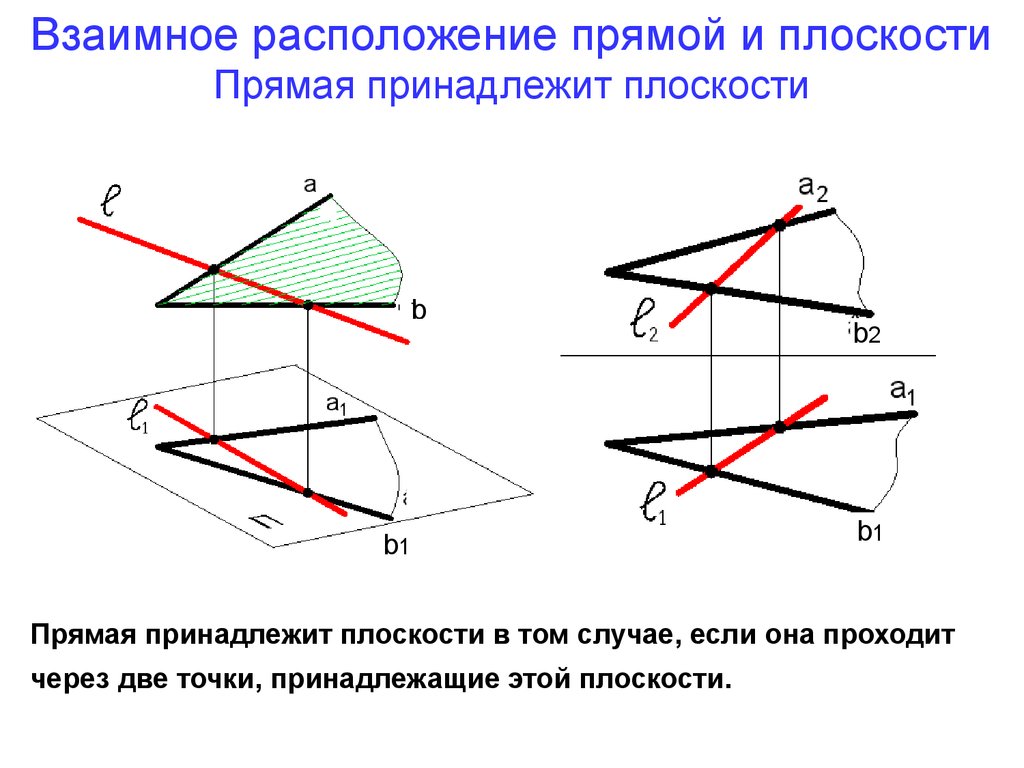
15. Взаимное расположение прямой и плоскости Прямая принадлежит плоскости

b
b1
b2
b1
Прямая принадлежит плоскости в том случае, если она проходит
через две точки, принадлежащие этой плоскости.

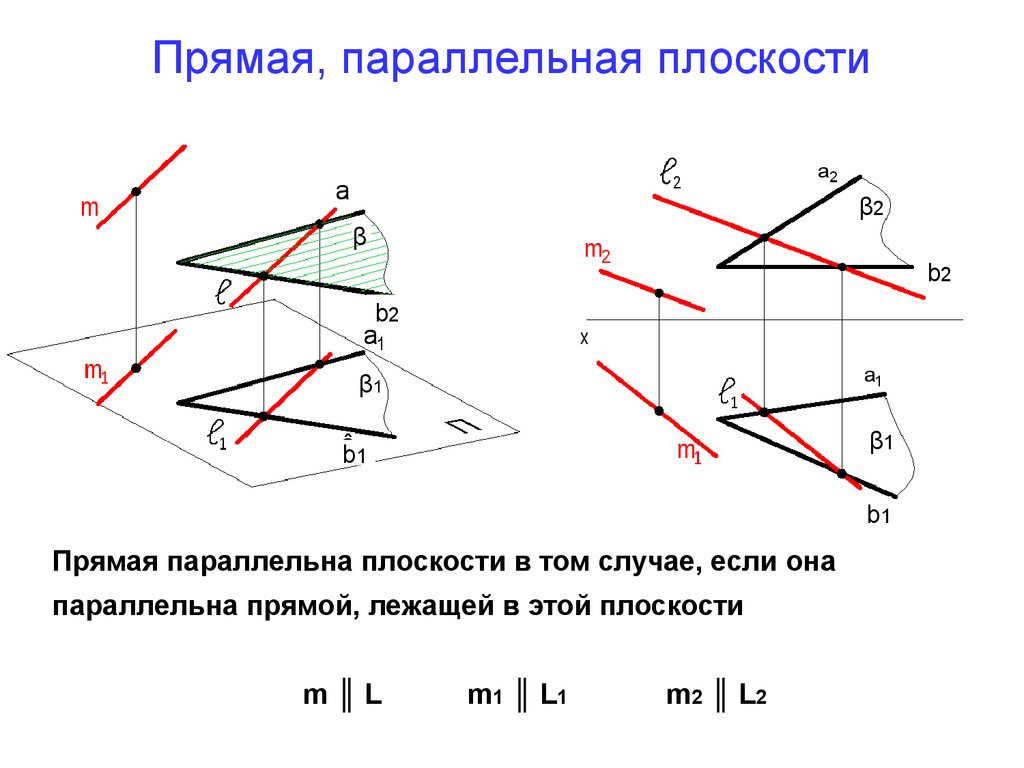
16. Прямая, параллельная плоскости

β2
β
b2
b2
β1
β1
b1
b1
Прямая параллельна плоскости в том случае, если она
параллельна прямой, лежащей в этой плоскости
m║L
m1 ║ L1
m2 ║ L2

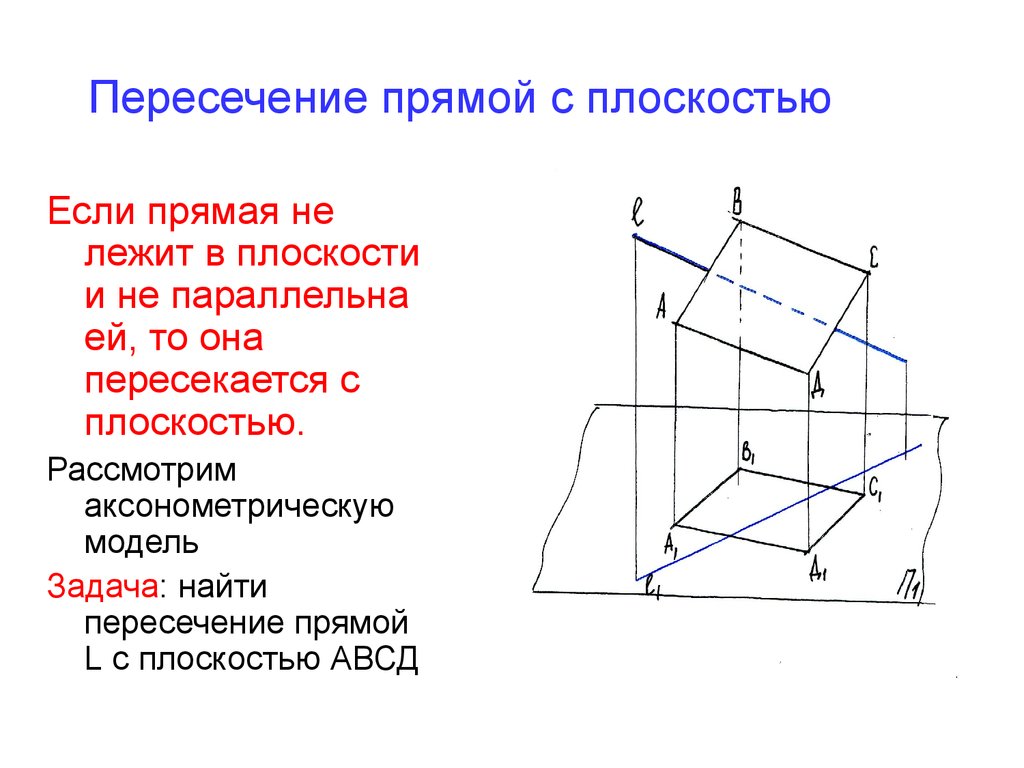
17. Пересечение прямой с плоскостью

Если прямая не
лежит в плоскости
и не параллельна
ей, то она
пересекается с
плоскостью.
Рассмотрим
аксонометрическую
модель
Задача: найти
пересечение прямой
L с плоскостью АВСД

18. Алгоритм решения задачи на пересечение прямой с плоскостью

1. Заключаем прямую во вспомогательную
проецирующую плоскость.
2. Строим линию пересечения двух плоскостей:
вспомогательной и заданной.
3. Находим точку пересечения прямой и
полученной линии пересечения.
4. Определяем видимость прямой.

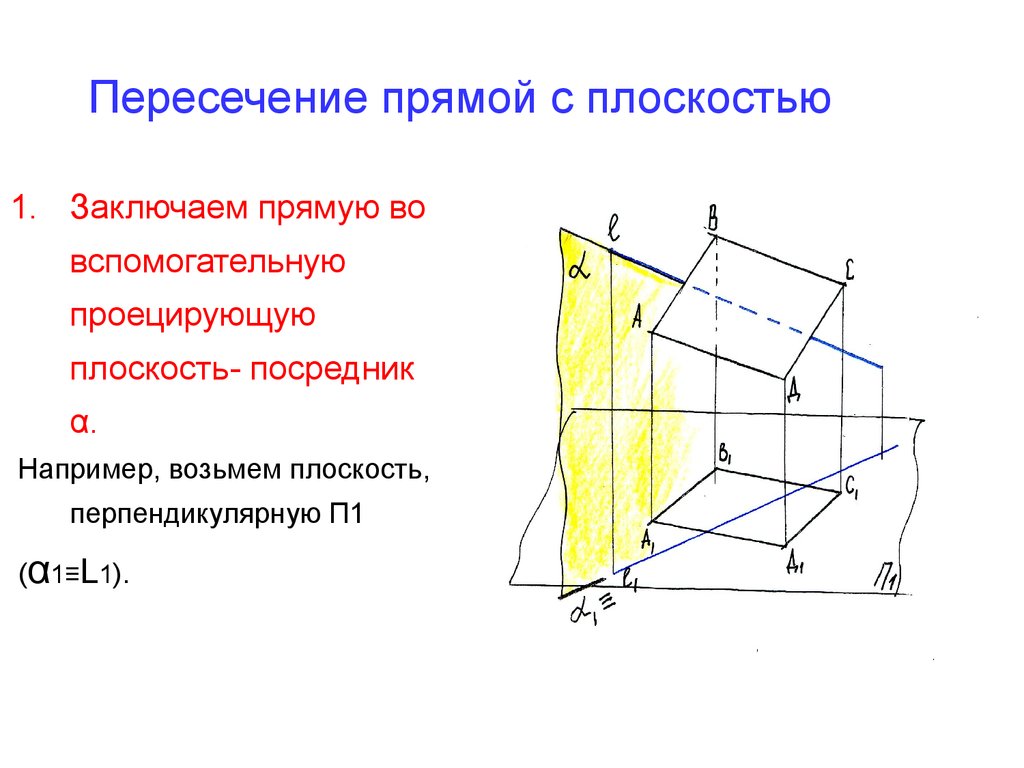
19. Пересечение прямой с плоскостью

1. Заключаем прямую во
вспомогательную
проецирующую
плоскость- посредник
α.
Например, возьмем плоскость,
перпендикулярную П1
(α1≡L1).

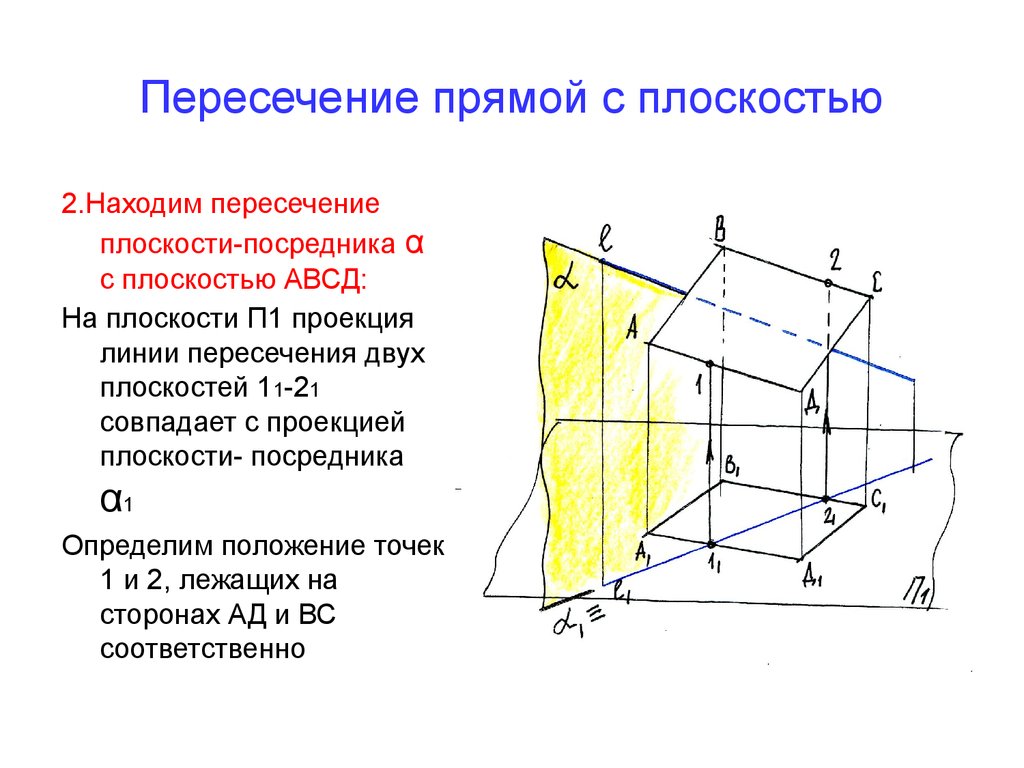
20. Пересечение прямой с плоскостью

2.Находим пересечение
плоскости-посредника α
с плоскостью АВСД:
На плоскости П1 проекция
линии пересечения двух
плоскостей 11-21
совпадает с проекцией
плоскости- посредника
α1
Определим положение точек
1 и 2, лежащих на
сторонах АД и ВС
соответственно

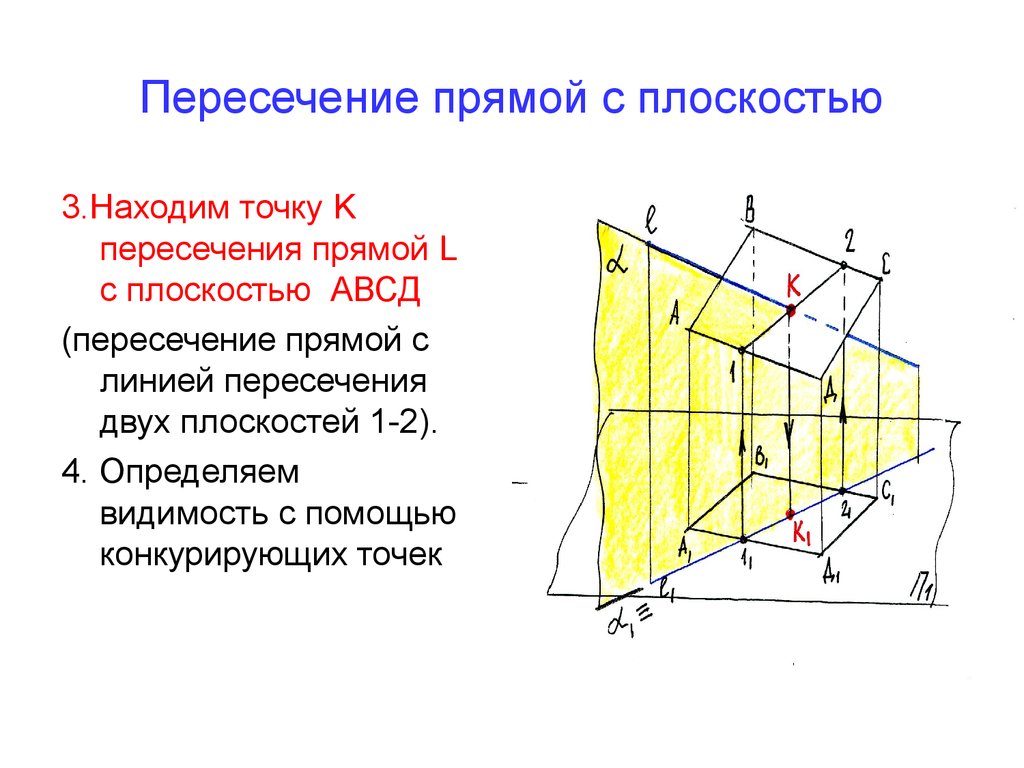
21. Пересечение прямой с плоскостью

3.Находим точку K
пересечения прямой L
с плоскостью АВСД
(пересечение прямой с
линией пересечения
двух плоскостей 1-2).
4. Определяем
видимость с помощью
конкурирующих точек

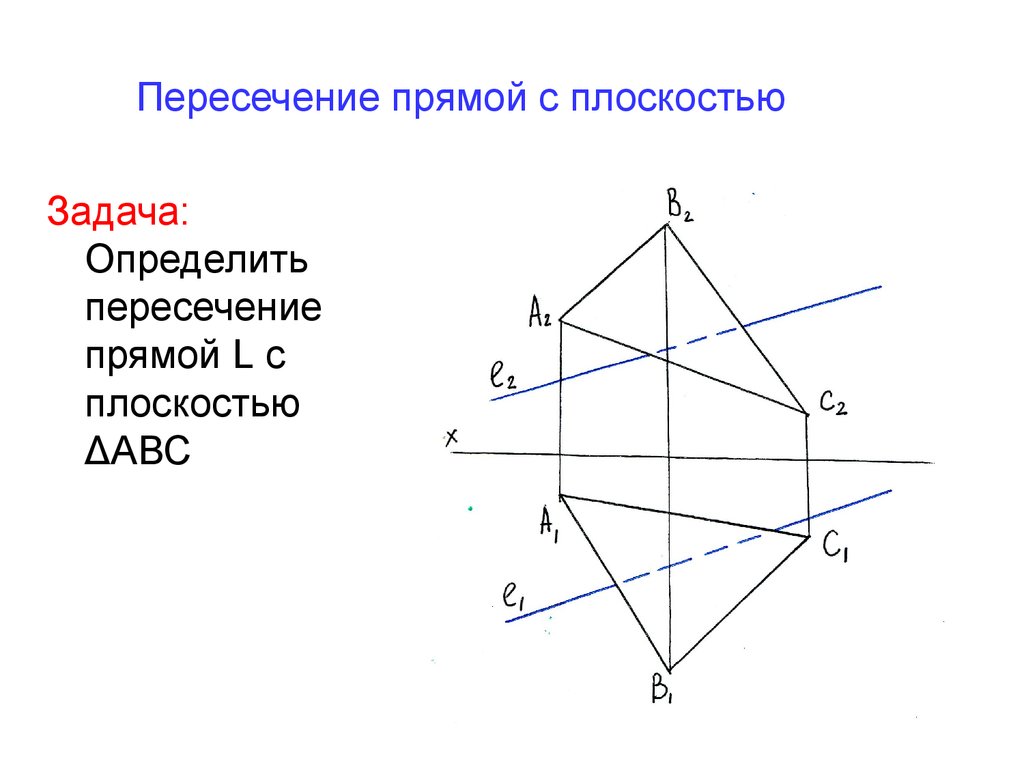
22. Пересечение прямой с плоскостью

Задача:
Определить
пересечение
прямой L с
плоскостью
ΔАВС

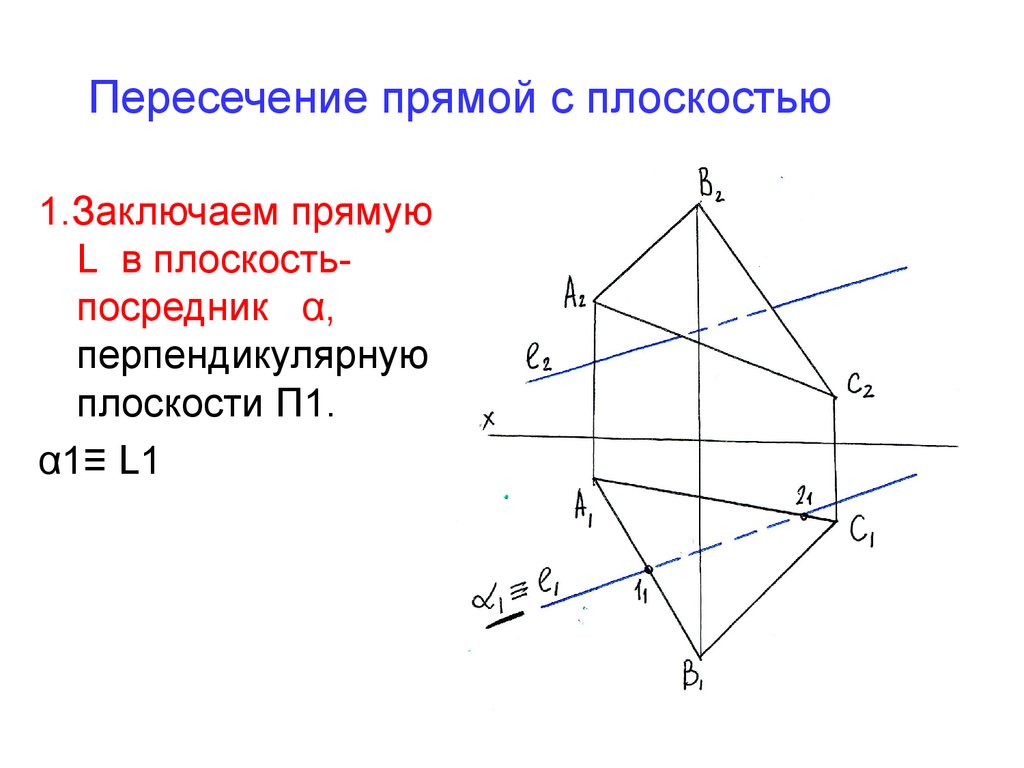
23. Пересечение прямой с плоскостью

1.Заключаем прямую
L в плоскостьпосредник α,
перпендикулярную
плоскости П1.
α1≡ L1

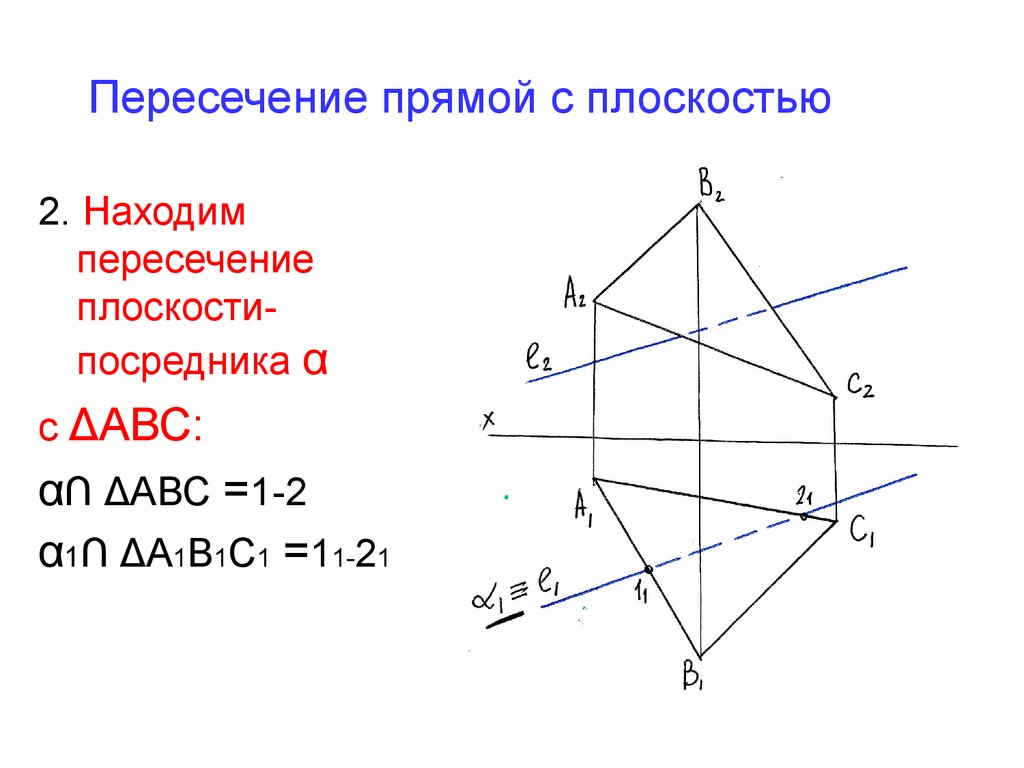
24. Пересечение прямой с плоскостью

2. Находим
пересечение
плоскостипосредника α
с ΔАВС:
α∩ ΔАВС =1-2
α1∩ ΔА1В1С1 =11-21

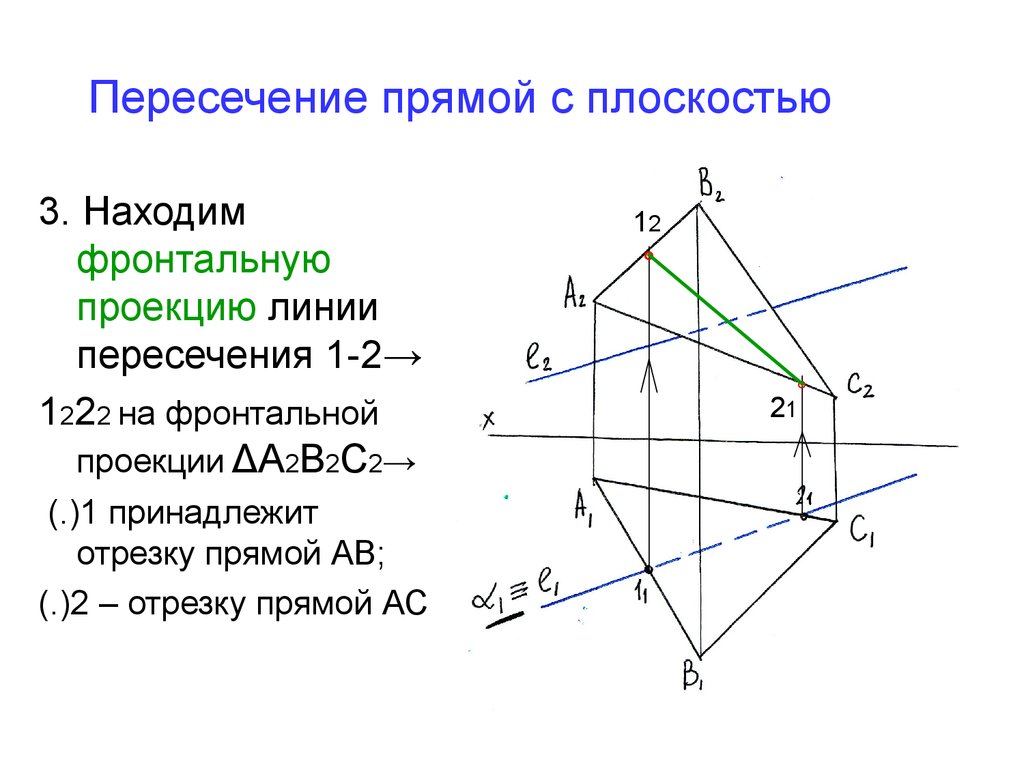
25. Пересечение прямой с плоскостью

3. Находим
фронтальную
проекцию линии
пересечения 1-2→
1222 на фронтальной
проекции ΔА2В2С2→
(.)1 принадлежит
отрезку прямой АВ;
(.)2 – отрезку прямой АС
12
°
°
21

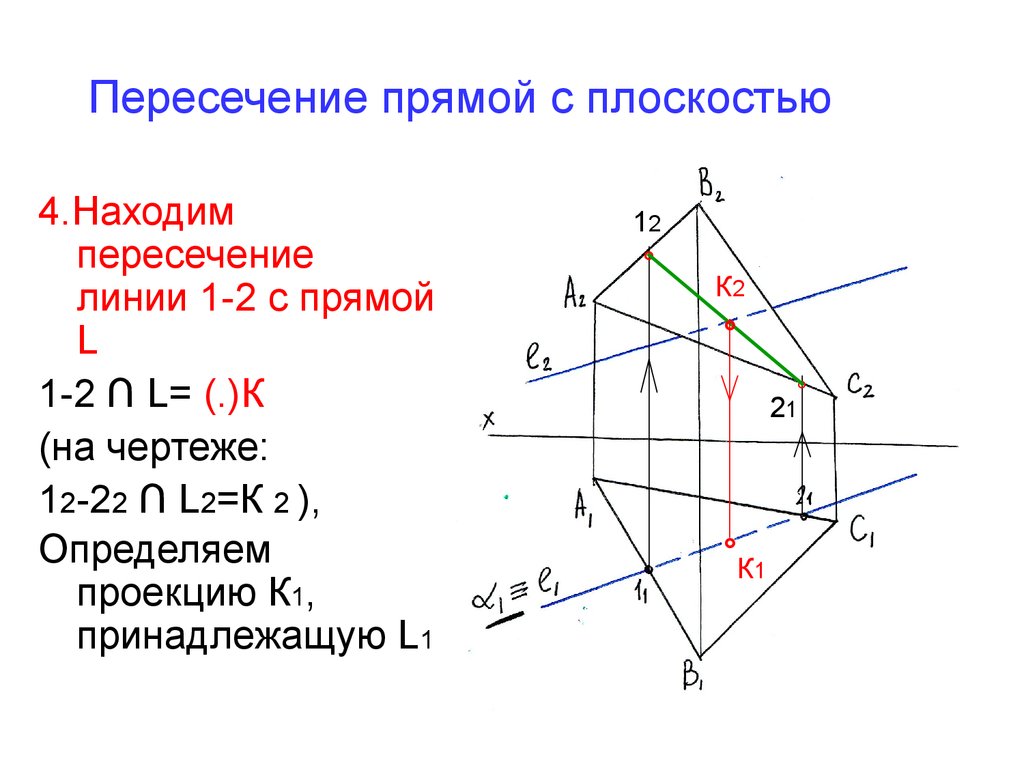
26. Пересечение прямой с плоскостью

4.Находим
пересечение
линии 1-2 с прямой
L
1-2 ∩ L= (.)К
(на чертеже:
12-22 ∩ L2=К 2 ),
Определяем
проекцию К1,
принадлежащую L1
12
°
К2
°
°
21
°К1

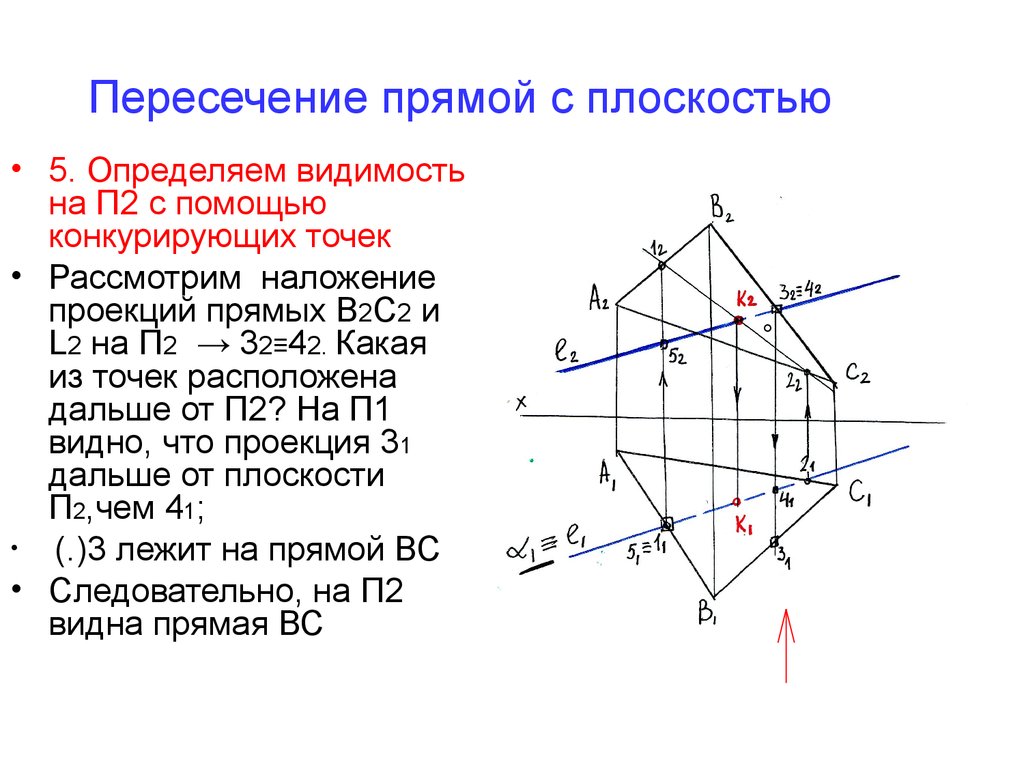
27. Пересечение прямой с плоскостью

• 5. Определяем видимость
на П2 с помощью
конкурирующих точек
• Рассмотрим наложение
проекций прямых В2С2 и
L2 на П2 → 32≡42. Какая
из точек расположена
дальше от П2? На П1
видно, что проекция 31
дальше от плоскости
П2,чем 41;
(.)3 лежит на прямой ВС
• Следовательно, на П2
видна прямая ВС
°

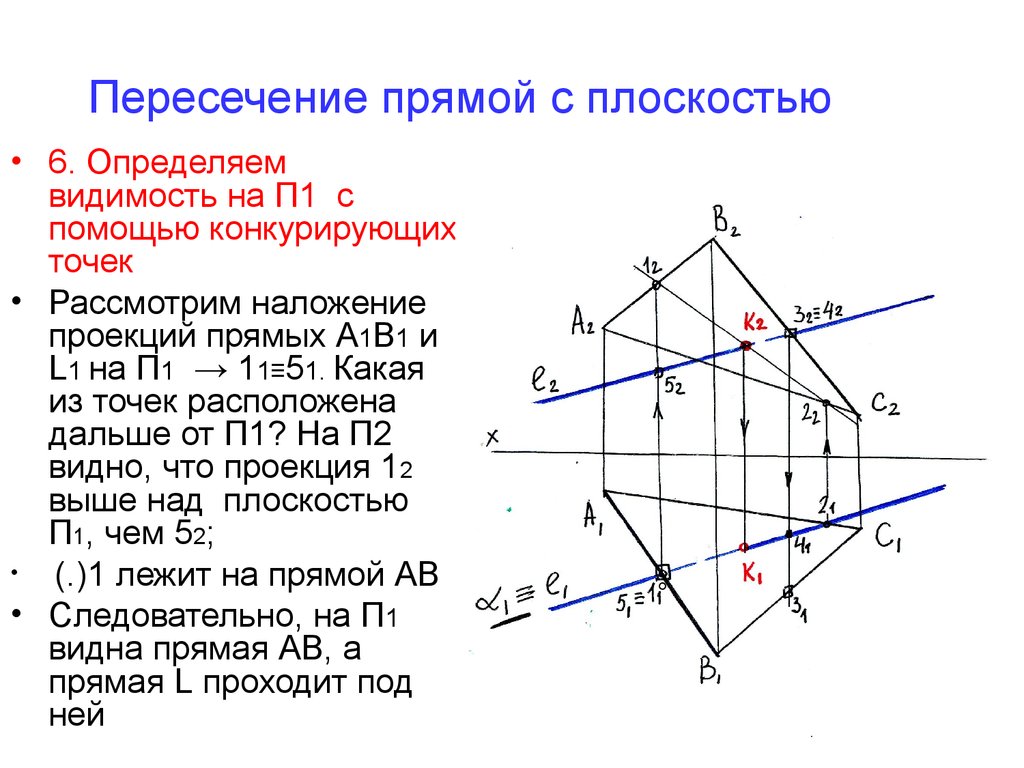
28. Пересечение прямой с плоскостью

• 6. Определяем
видимость на П1 с
помощью конкурирующих
точек
• Рассмотрим наложение
проекций прямых А1В1 и
L1 на П1 → 11≡51. Какая
из точек расположена
дальше от П1? На П2
видно, что проекция 12
выше над плоскостью
П1, чем 52;
(.)1 лежит на прямой АВ
• Следовательно, на П1
видна прямая АВ, а
прямая L проходит под
ней
°

29.

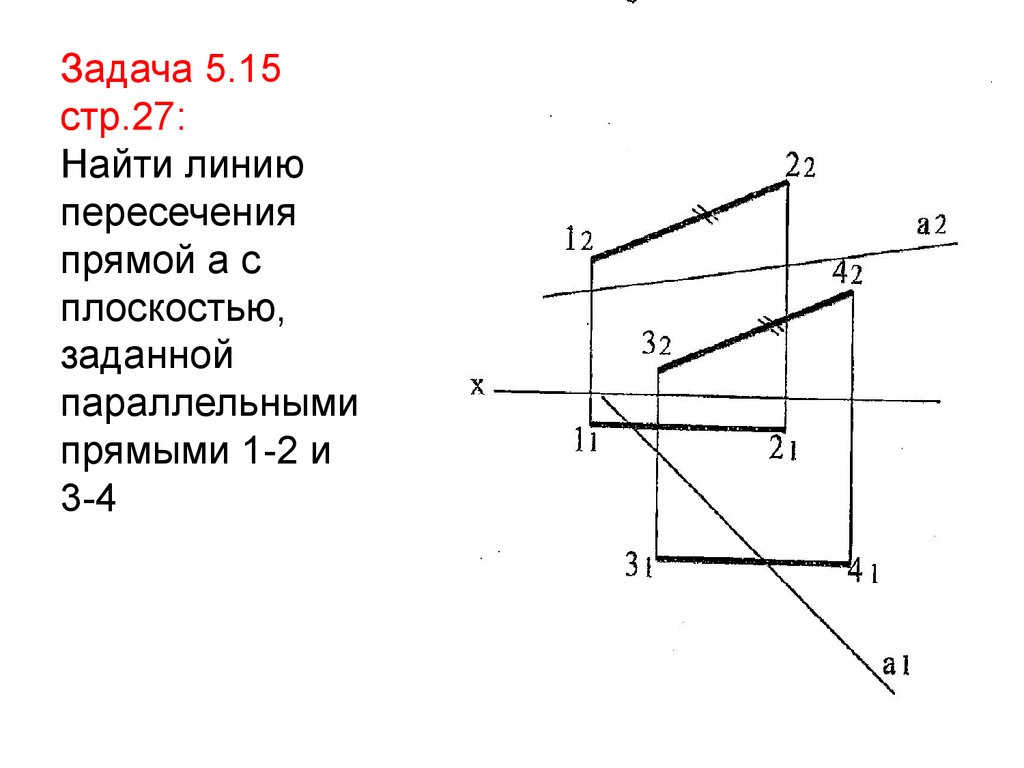
Задача 5.15
стр.27:
Найти линию
пересечения
прямой а с
плоскостью,
заданной
параллельными
прямыми 1-2 и
3-4

30.

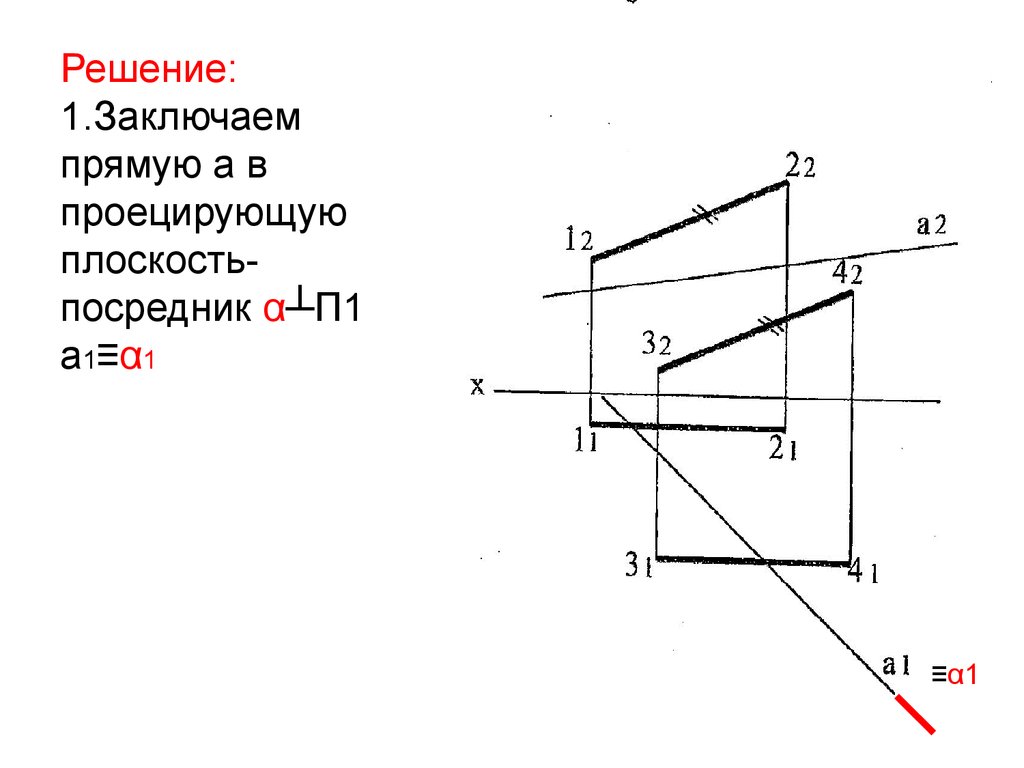
Решение:
1.Заключаем
прямую а в
проецирующую
плоскостьпосредник α┴П1
а1≡α1
≡α1

31.

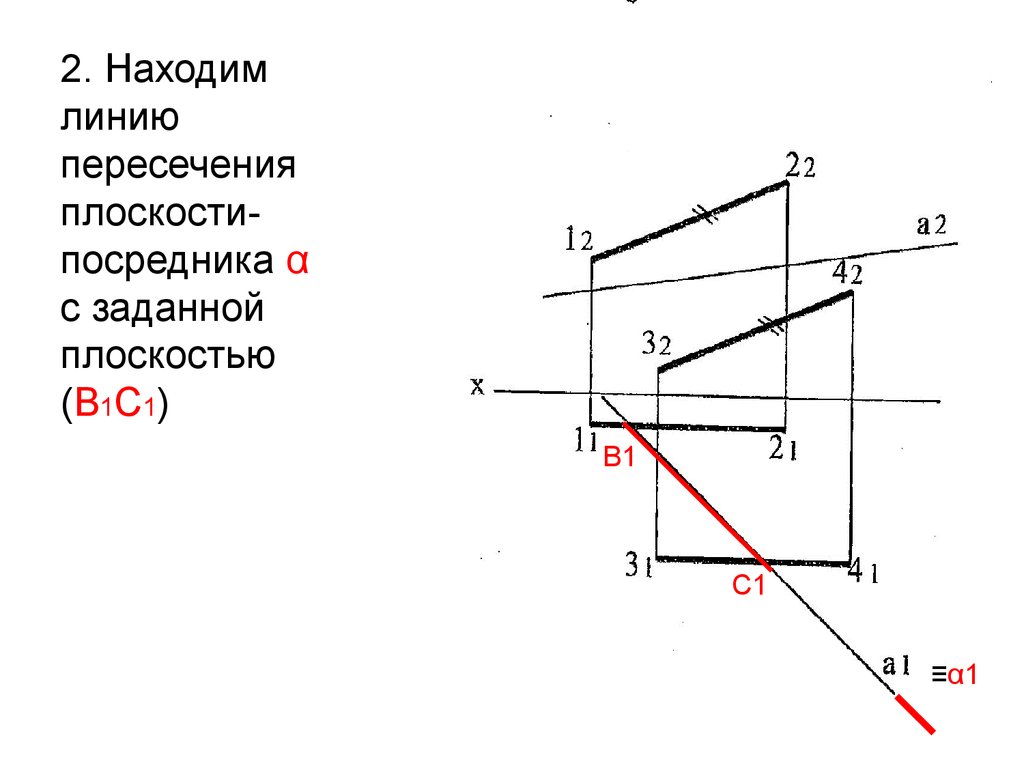
2. Находим
линию
пересечения
плоскостипосредника α
с заданной
плоскостью
(В1С1)
В1
С1
≡α1

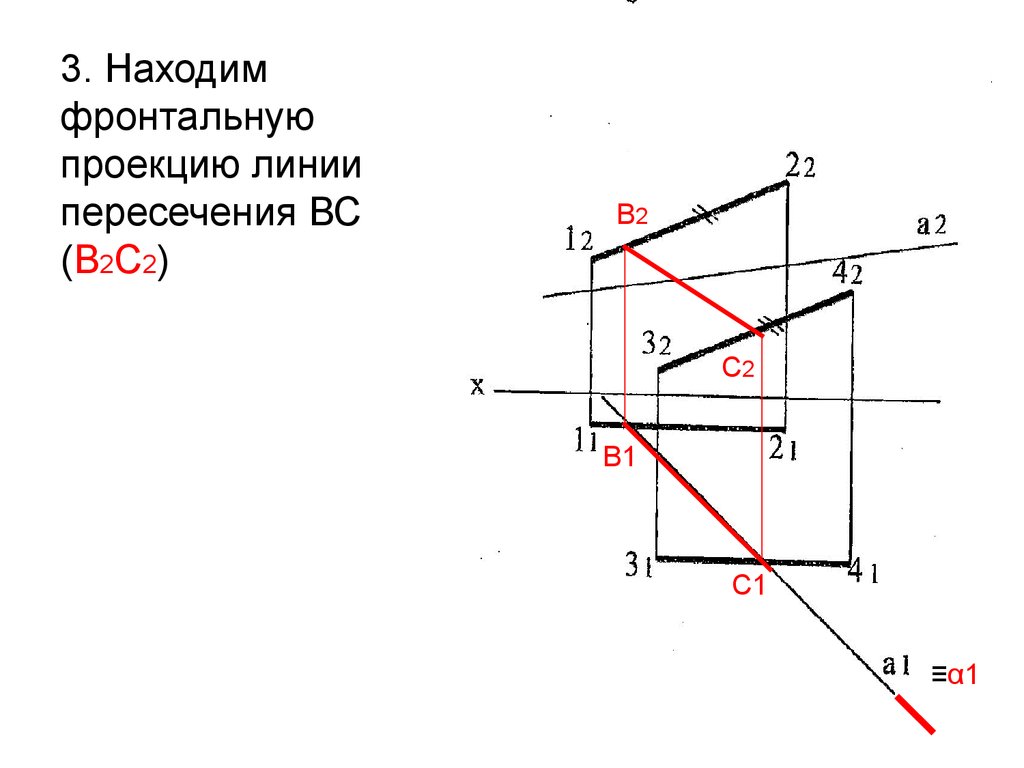
32.

3. Находим
фронтальную
проекцию линии
пересечения ВС
(В2С2)
В2
С2
В1
С1
≡α1

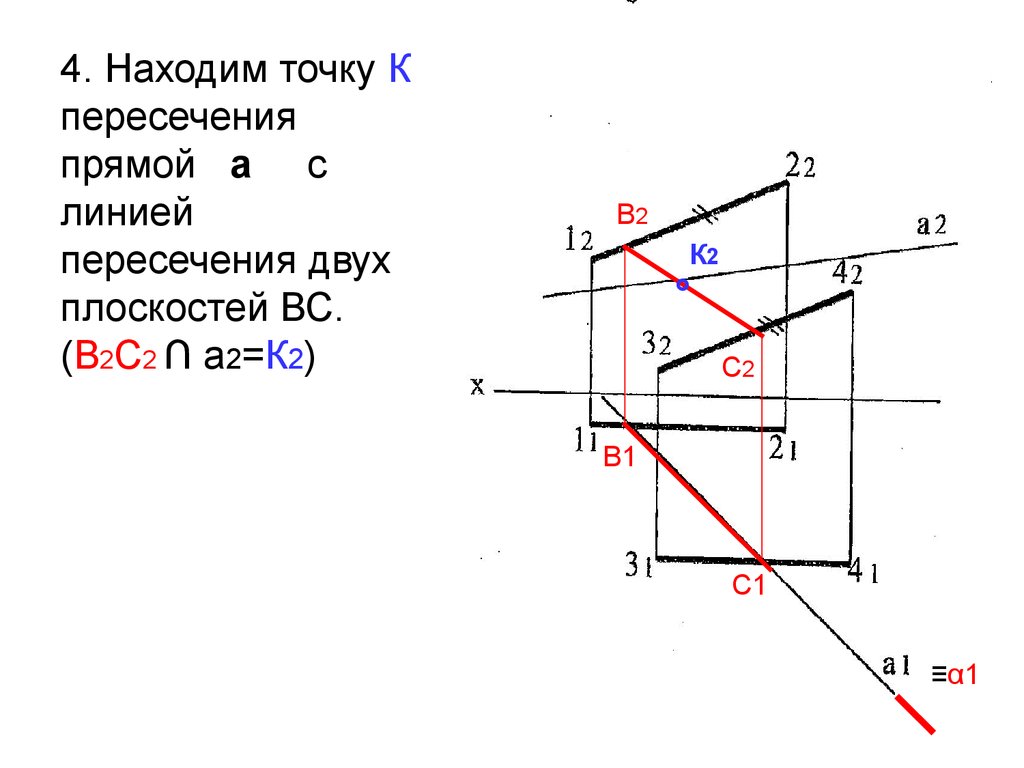
33.

4. Находим точку К
пересечения
прямой а с
линией
пересечения двух
плоскостей ВС.
(В2С2 ∩ а2=К2)
В2
К2
°
С2
В1
С1
≡α1

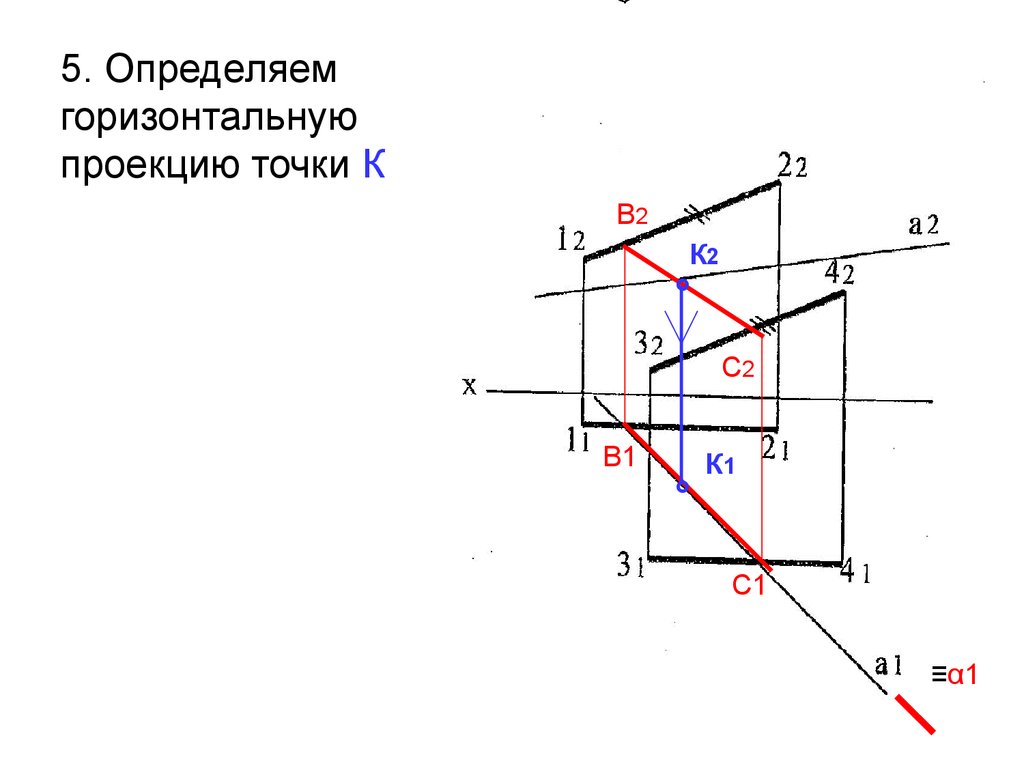
34.

5. Определяем
горизонтальную
проекцию точки К
В2
К2
°
С2
В1
°
К1
С1
≡α1

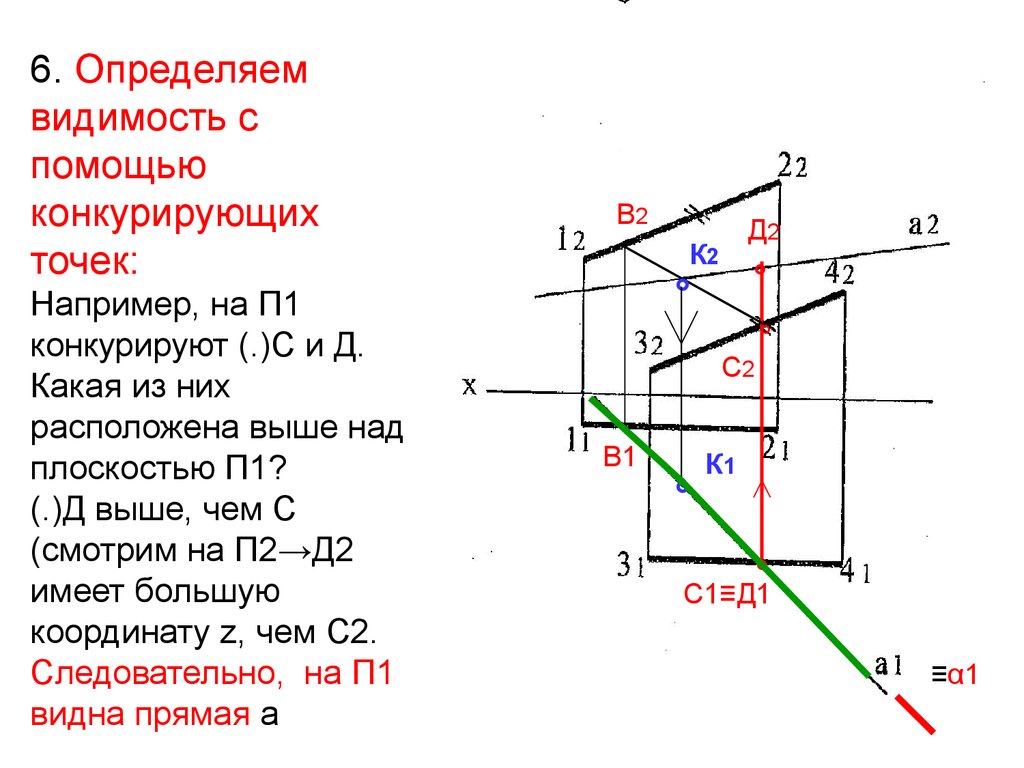
35.

6. Определяем
видимость с
помощью
конкурирующих
точек:
Например, на П1
конкурируют (.)С и Д.
Какая из них
расположена выше над
плоскостью П1?
(.)Д выше, чем С
(смотрим на П2→Д2
имеет большую
координату z, чем С2.
Следовательно, на П1
видна прямая а
В2
Д2
К2
°
°
С2
В1
°
°
К1
°
С1≡Д1
≡α1

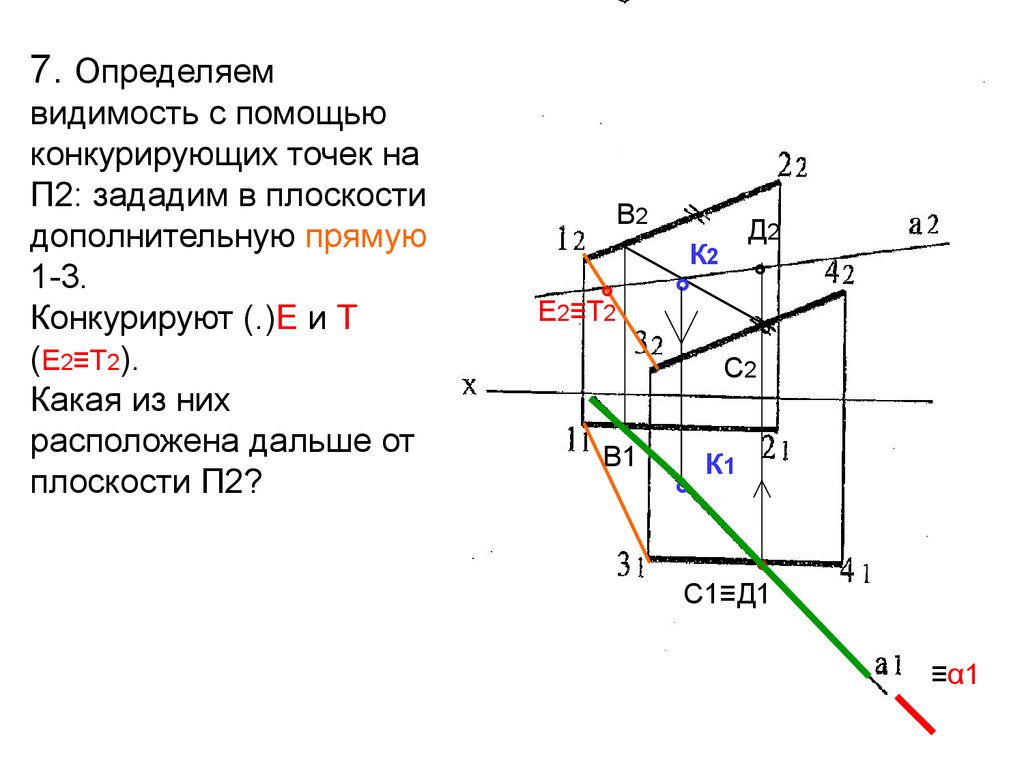
36.

7. Определяем
видимость с помощью
конкурирующих точек на
П2: зададим в плоскости
дополнительную прямую
1-3.
Конкурируют (.)Е и Т
(Е2≡Т2).
Какая из них
расположена дальше от
плоскости П2?
В2
Д2
К2
Е2≡Т°2
°
°
°
С2
В1
°
К1
°
С1≡Д1
≡α1

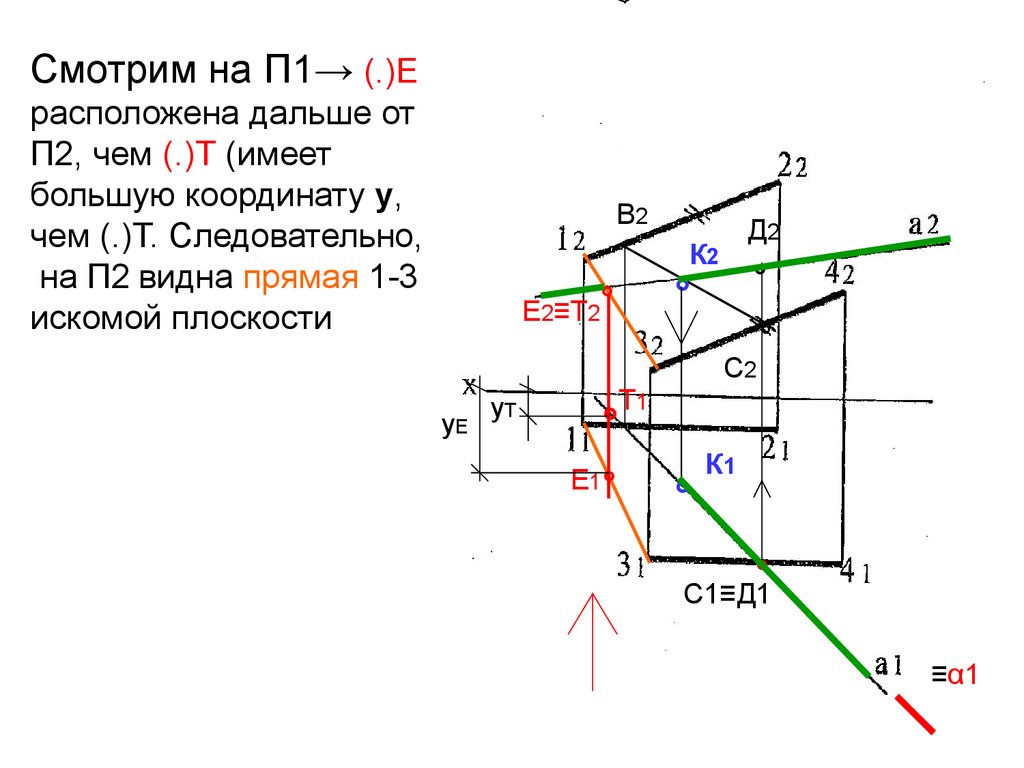
37.

Смотрим на П1→ (.)Е
расположена дальше от
П2, чем (.)Т (имеет
большую координату у,
чем (.)Т. Следовательно,
на П2 видна прямая 1-3
искомой плоскости
В2
Д2
К2
°
°
Е2≡Т2°
°
С2
уЕ
уТ
°
Е1°
Т1
°
К1
°
С1≡Д1
≡α1