Похожие презентации:
Вычисление неопределенного интеграла
1.
Вычислениенеопределенного
интеграла
2.
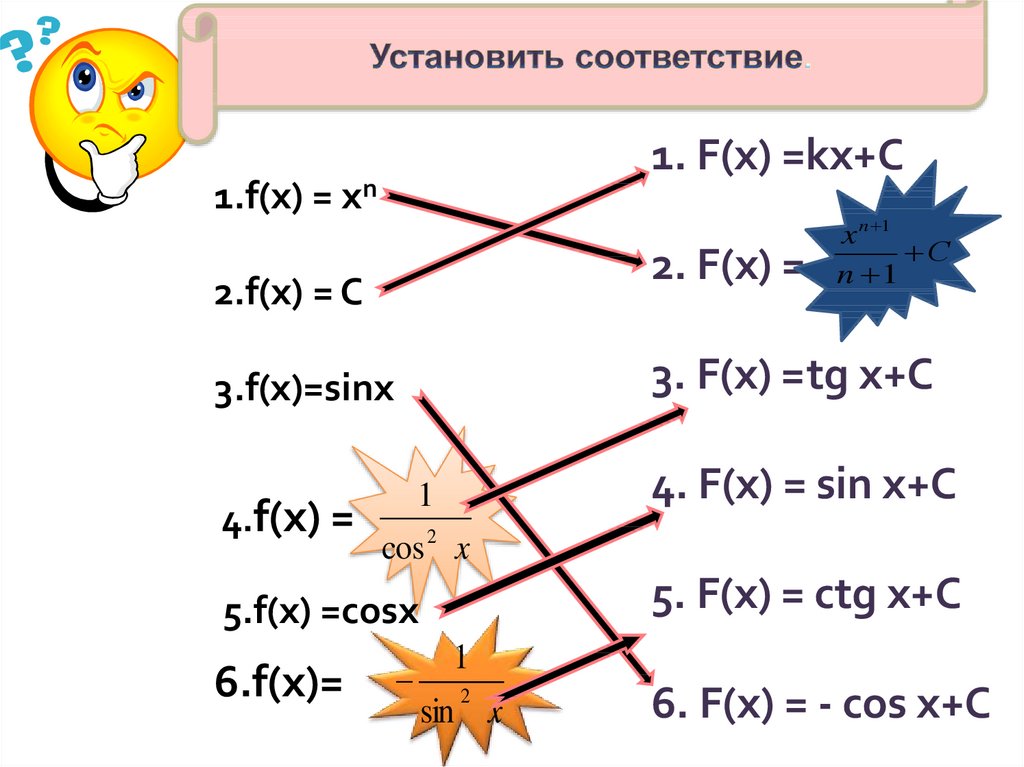
1. F(x) =kх+С1.f(x) = хn
2. F(x) =
2.f(x) = C
3. F(x) = tg x+С
3.f(x)=sinx
4.f(x) =
4. F(x) = sin x+С
1
cos 2 x
5. F(x) = сtg x+С
5.f(x) =cosx
6.f(x)=
x n 1
С
n 1
1
2
sin x
6. F(x) = - cos x+С
3. Найти первообразные для функций:
1) f(x) =10х2) f(x) =3 х²
3) f(x) = sinх+5
4) f(x) = 5cosx
5) f(x) = 6х²
6) f(x) = 3-2х
4.
ЗаданиеУстановить соответствие. Найти такой общий вид
первообразной, которая соответствует заданной
функции.
x
1. F x cos x C
2
3
1. f x x x
x2
x4
2. F ( x )
C
2
4
2. f x 2 cos x
5 x 2 10 x 3
3.F ( x ) 8 x
C
2
3
2
4. F ( x ) 2 sin x C
3. f x 8 5 x 10 x
4. f x 4 3x
9
10 x 2
5.F ( x ) 8 x sin x
C
3
1
10
6. F ( x )
4
3
x
C
30
1
10
7. F ( x ) 4 3 x C
3
5.
Неопределенным интегралом от непрерывнойфункции f(x) на интервале (a; b) называют
совокупность первообразных функции.
f
(
x
)
dx
F
(
x
)
c
Где С – произвольная постоянная (const).
6.
Операция нахождения неопределенного интеграла отфункции называется интегрированием этой функции
.
7.
8.
В развитии интегрального исчисленияприняли участие русские математики:
В.Я. Буняковский
(1804 – 1889)
М.В. Остроградский
(1801 – 1862)
П.Л. Чебышев
(1821 – 1894)
9.
Примеры1. Adx Ax C ; Ax C A
x
x
x
x
2. e dx e С; e C e
3. sin xdx cos x С ;
4
x
4. x dx
С;
4
3
cos x C
sin x
tg x C
1
2
cos x
x
1
С 4x 3 x 3
4
4
1
5.
dx tg x C ;
2
cos x
4
10.
11.
Свойства интегралаf
(
x
)
dx
g
(
x
)
dx
(
f
(
x
)
g
(
x
)
)
dx
Cf
(
x
)
dx
C
f
(
x
)
dx
12.
Свойства интегралаf ( х)dx
f ( х)
1
f (kx b)dx F (kx b) C
k
13. Верно ли что:
а)x
dx
5
x
C
5
4
б)
в)
3
x
dx
x
C
2
3
г) г)
3
x
dx
6
x
C
2
1 7
x dx 7 x C
6
14.
Пример. Вычислить x 3x x 1 dx .Решение. Так как под знаком интеграла
находится сумма четырех слагаемых, то
раскладываем интеграл на сумму четырех
интегралов:
2
3
2
3
2
3
x 3 x x 1 dx x dx 3 x dx xdx dx .
3
4
2
x
x
x
3
x C
3
4
2
15. Пример №2
6x
3
x 1 dx 6 x dx xdx 1dx
4
2
3
3 4 1 2
x
x
6 x C x x x C
2
2
4
2
16. Пример №3
dxx 3
ln x 3 C
(формула 4 таблицы интегралов)
17. Пример №4
13
x
1
3
x
1
dx
C
3
25
25
24
(формула 3)
18. Пример №5
16
(2 3 x) C.
(2 3x) dx
3 6
5
19.
Пример №1න 3







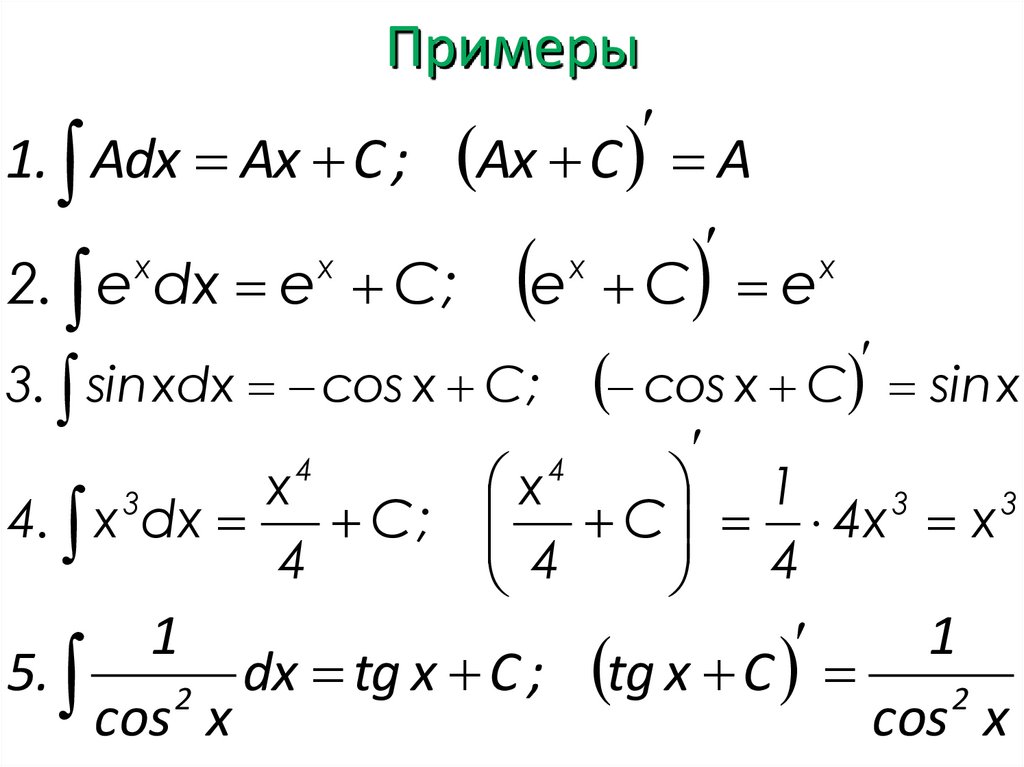





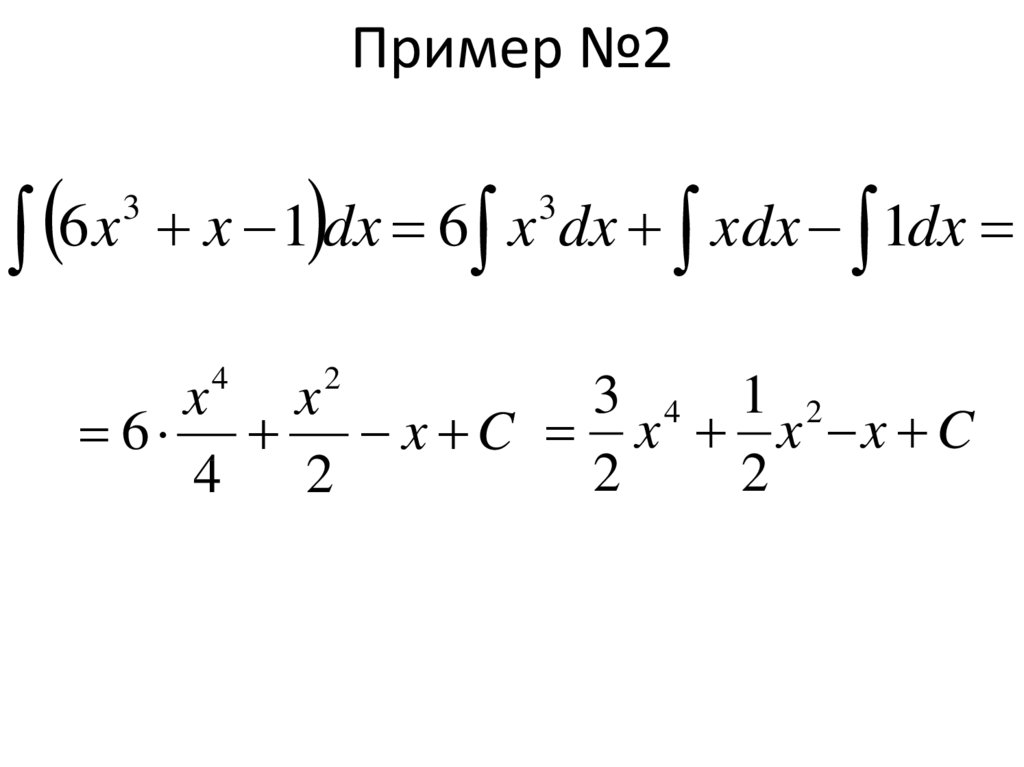







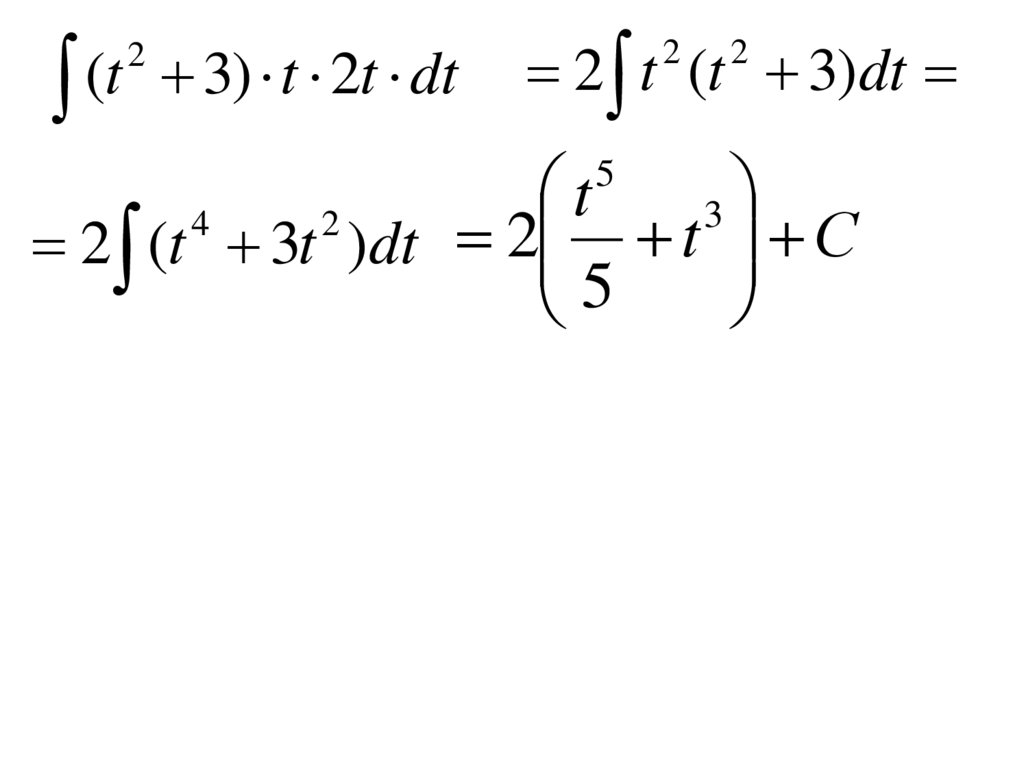

 Математика
Математика








