Дробно-линейная функция

1. Домашнее задание

П. 49 – 52,
№1210 (е),
№1212 (г),
№1213 (г),

2. Дробно-линейная функция

11.05.2020
Дробно-линейная функция

3. Вспомним параллельный перенос, сжатие и растяжение графиков функций

№1210 (д)
сдвиг вниз
сдвиг влево
Единичный отрезок – одна клетка, оси подписать.

4.

X
-4
-1
0
1
4
Y
4
1
0
1
4
таблица зависимости

5.

6.

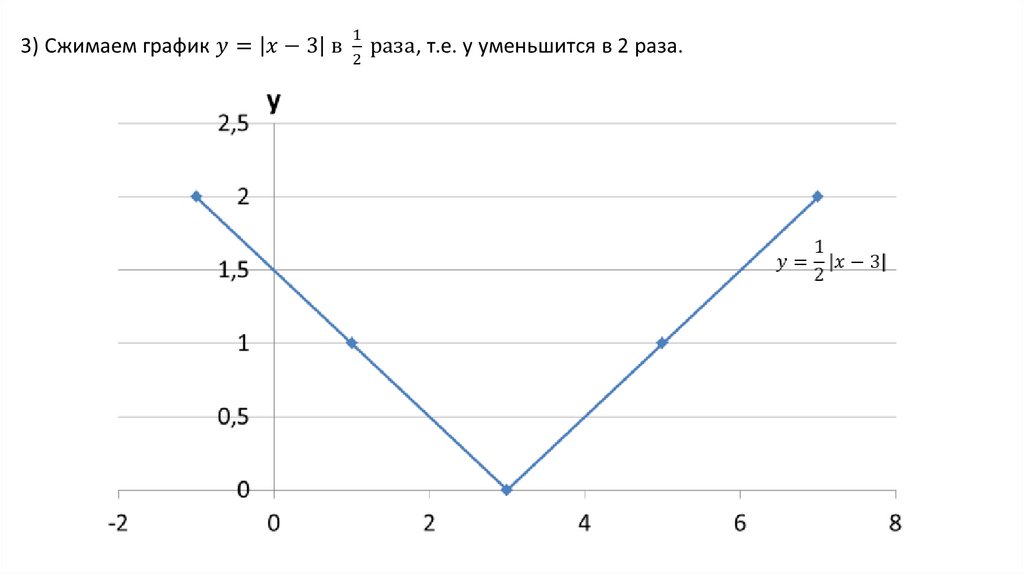
№1212 (в)
сжатие
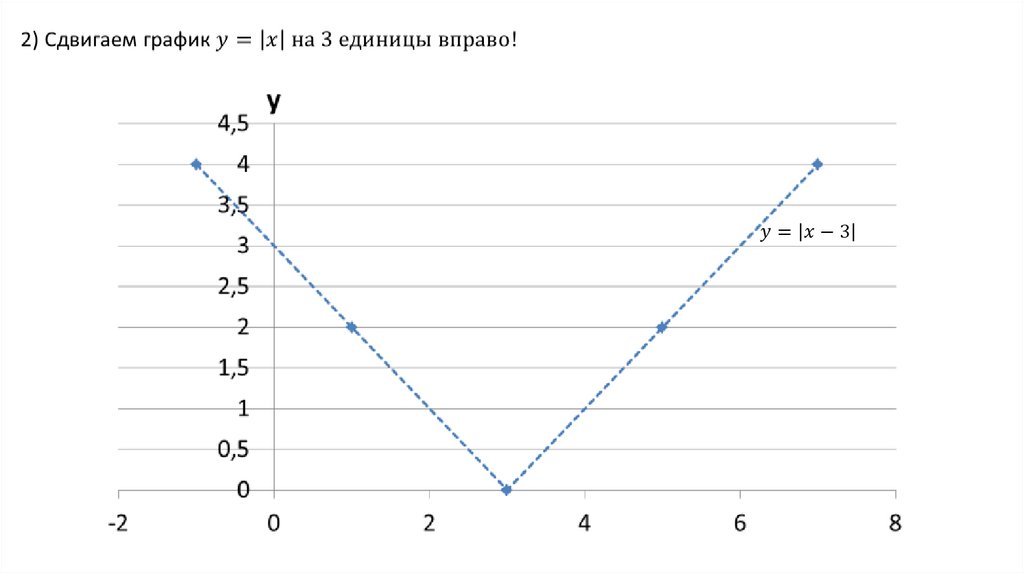
сдвиг вправо
Единичный отрезок – одна клетка, оси подписать.

7.

X
-4
-1
0
1
4
Y
4
1
0
1
4
таблица зависимости

8.

9.

10.

Выполним задания данного номера:
1) найдем нули функции (это значения аргумента х при которых значение функции равно нулю у = 0)
Ответ: х = 3; х (-∞; 0) (0; +∞)

11.

№1213 (в)
сдвиг вверх
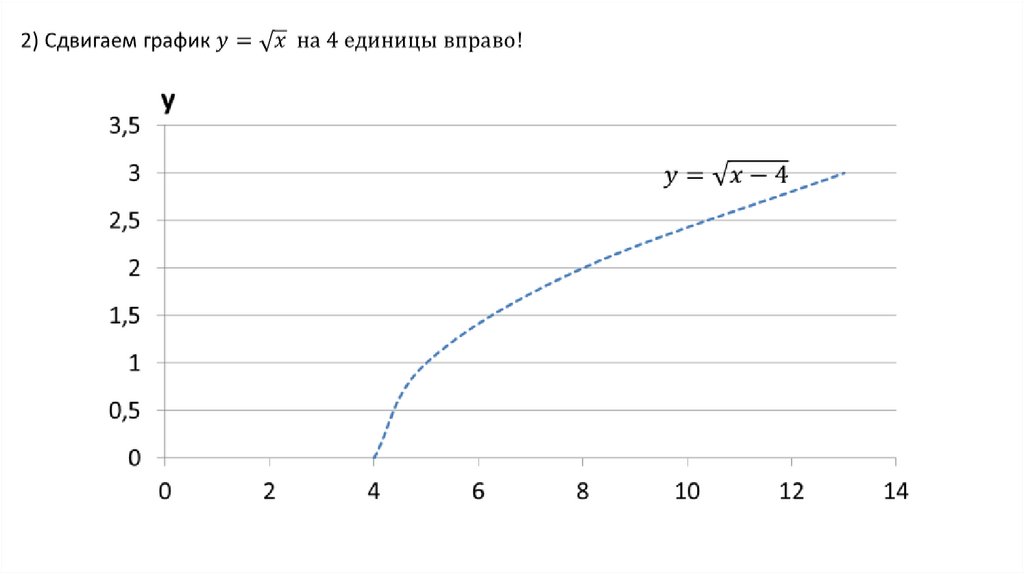
сдвиг вправо
Единичный отрезок – одна клетка, оси подписать.

12.

X
0
1
4
9
Y
0
1
2
3
таблица зависимости

13.

14.

Ответ на вопрос: данный график не имеет точек во II, III, IV четвертях

15.

Изучение новой темы

16.

Вспомнить: функция обратной пропорциональности
Свойство:

17.

На графике это свойство проявляется в том, что точки графика
по мере их удаления в бесконечность неограниченно
приближаются к оси x.

18.

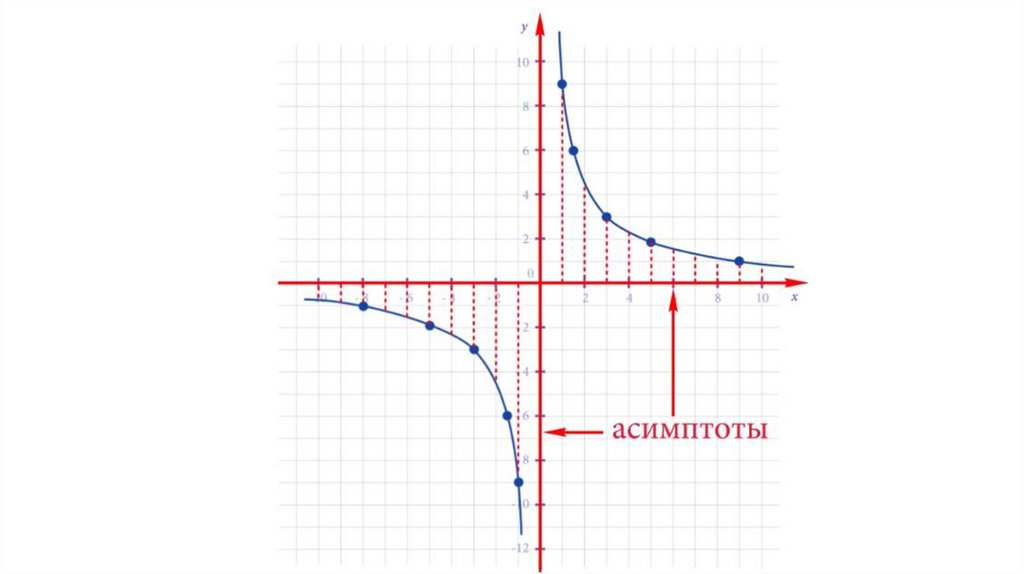
Асимптота кривой - прямая,
к которой приближаются как угодно близко
точки кривой по мере их удаления
в бесконечность.

19.

20.

21.

Дробно-линейные функции
многочлен первой
степени или число,
отличное от нуля
многочлен первой степени.

22.

Дробно-линейные функции
a, b, c, d — произвольные числа
c, ≠ 0, ad – bc ≠ 0
!

23.

Если с = 0, получается линейная функция.
Если ad – dc = 0, получается сократимая дробь
ad – dc = 0
ad = dc
a=c
константа

24.

Вспомните!
График функции y = f(x) + n можно получить из
графика функции y = f(x) с помощью параллельного
переноса вдоль оси y на |n| единиц вверх, если n > 0, и
на |n| единиц вниз, если n < 0.
График функции y = f(x + m) можно получить из
графика функции y = f(x) с помощью сдвига вдоль оси
x на |m | единиц вправо, eсли m < 0, и на |m | eдиниц
влево, eсли m > 0.

25.

Графиком дробно-линейной функции является
гипербола, которую можно получить из гиперболы
с помощью параллельных переносов вдоль координатных осей.

26.

27.

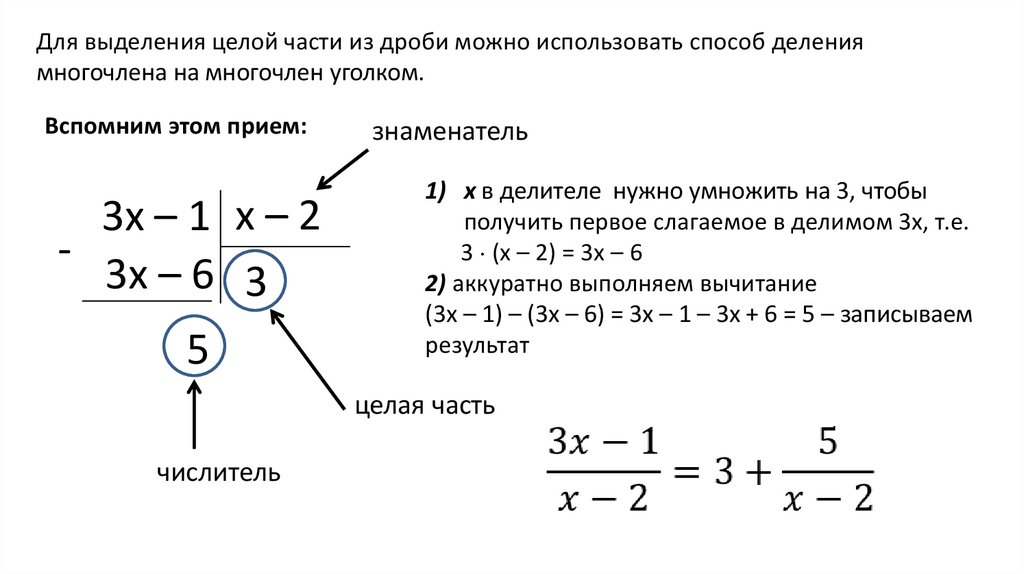
Для выделения целой части из дроби можно использовать способ деления
многочлена на многочлен уголком.
Вспомним этом прием:
3х – 1 х – 2
3х – 6 3
5
знаменатель
1) х в делителе нужно умножить на 3, чтобы
получить первое слагаемое в делимом 3х, т.е.
3 (х – 2) = 3х – 6
2) аккуратно выполняем вычитание
(3х – 1) – (3х – 6) = 3х – 1 – 3х + 6 = 5 – записываем
результат
целая часть
числитель

28.

— сдвига полученного графика на 2 единицы вправо вдоль оси x;
— сдвига полученного графика на 3 единицы вверх в направлении оси y.

29.

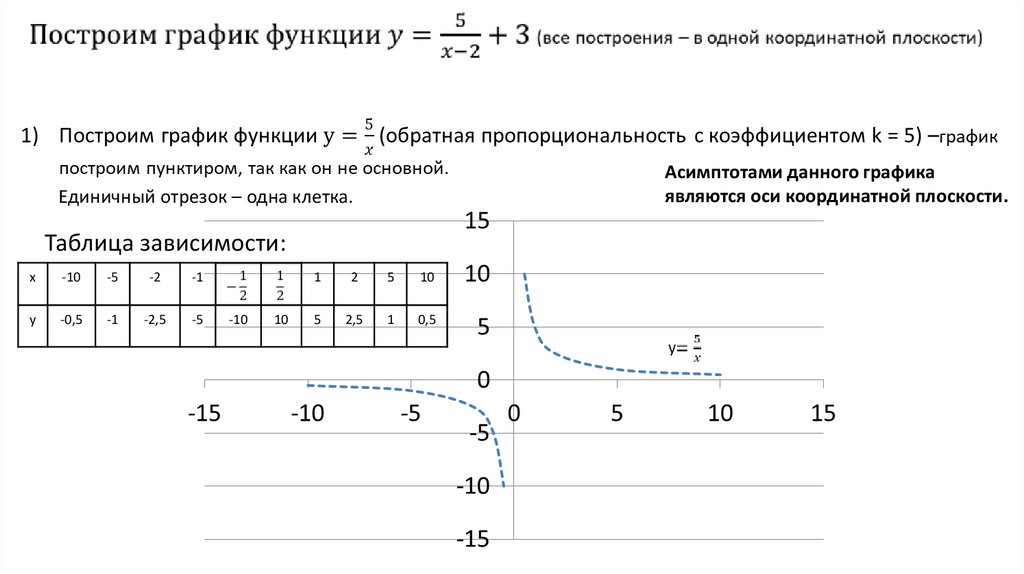
Асимптотами данного графика
являются оси координатной плоскости.
Единичный отрезок – одна клетка.
Таблица зависимости:
х
-10
-5
-2
-1
у
-0,5
-1
-2,5
-5
-10
10
1
2
5
10
5
2,5
1
0,5

30.

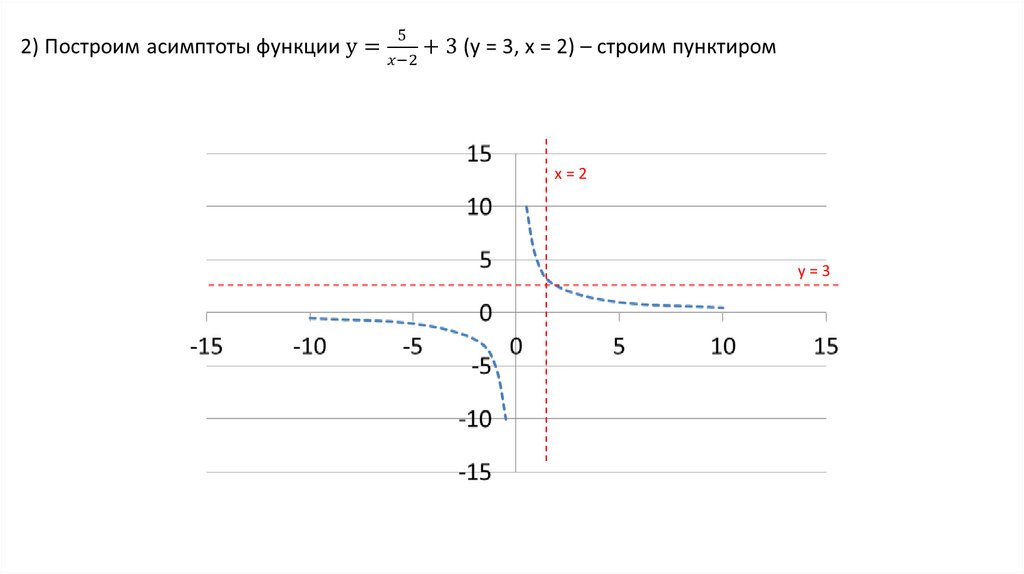
х=2
у=3

31.

1) сдвиг графика на 2 единицы вправо вдоль оси ОХ;
2) сдвига полученного графика на 3 единицы вверх вдоль оси ОУ.
х=2
Основной график строим сплошной линией
(можно другим цветом)
у=3