Похожие презентации:
Свойства функции y=cos-x и ее график
1.
y- 2π
-π
0
x
π
2π
1
2. Свойства функции
1.D(y)
2.E(y)
3. Четность функции
4. Периодичность функции
5.Нули функции
6. Наибольшее значение
7. Наименьшее значение
8. Положительные значения
9. Отрицательные значения
10. Возрастание функции
11. Убывание функции
2
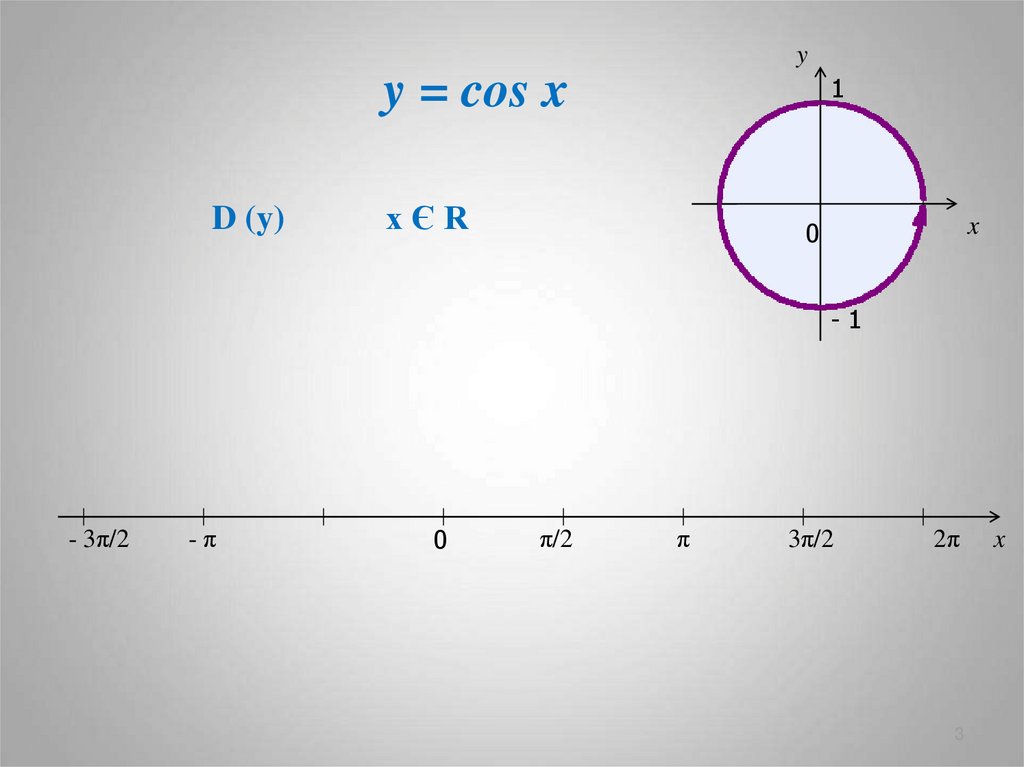
3. y = cos x
yy = cos x
D (y)
1
xЄR
x
0
-1
- 3π/2
-π
0
π/2
π
3π/2
2π
3
x
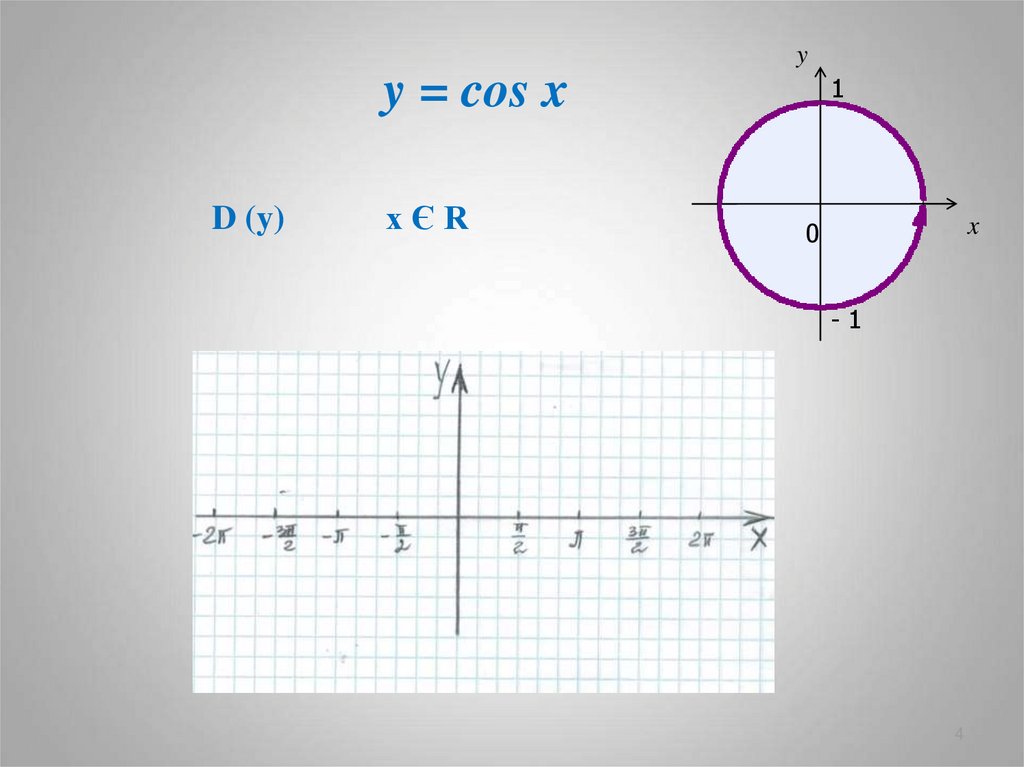
4. y = cos x
yy = cos x
D (y)
xЄR
1
x
0
-1
4
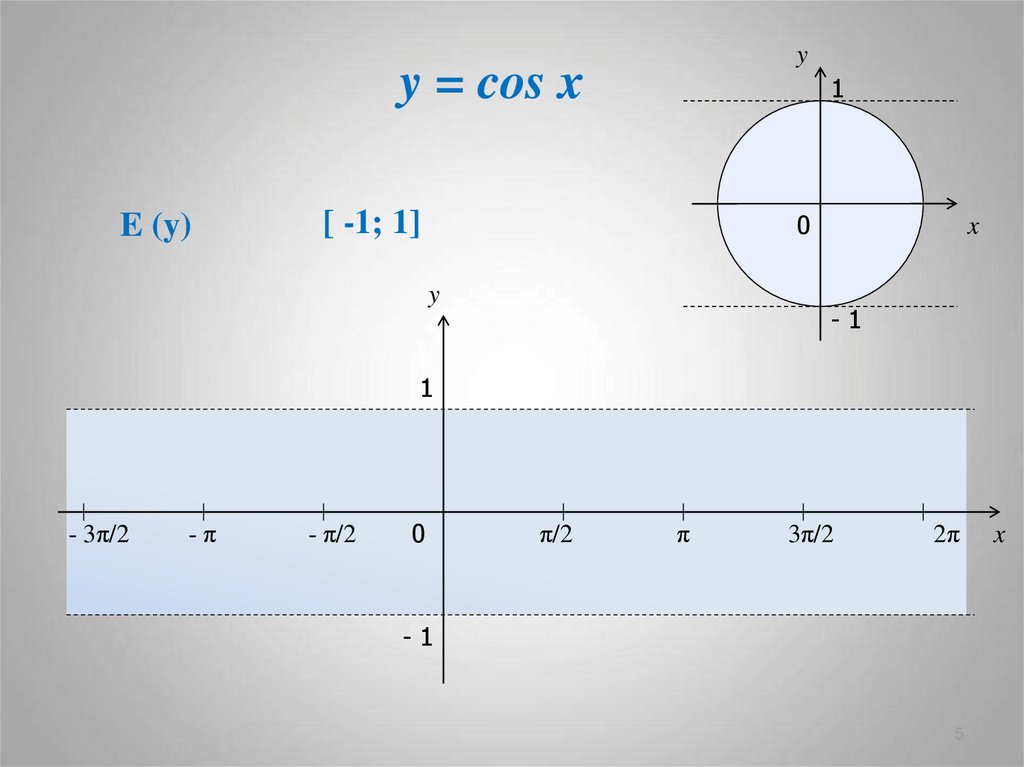
5. y = cos x
yy = cos x
E (y)
1
0
[ -1; 1]
y
x
-1
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
5
x
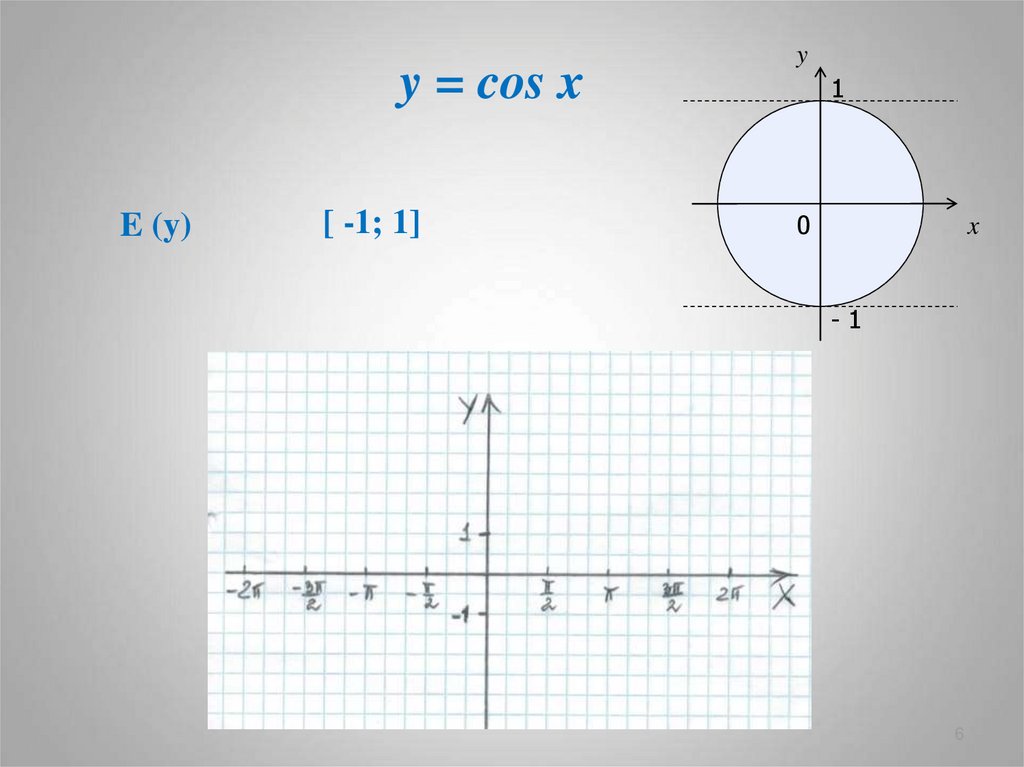
6. y = cos x
E (y)[ -1; 1]
y
1
0
x
-1
6
7. y = sin x
yy = sin x
1
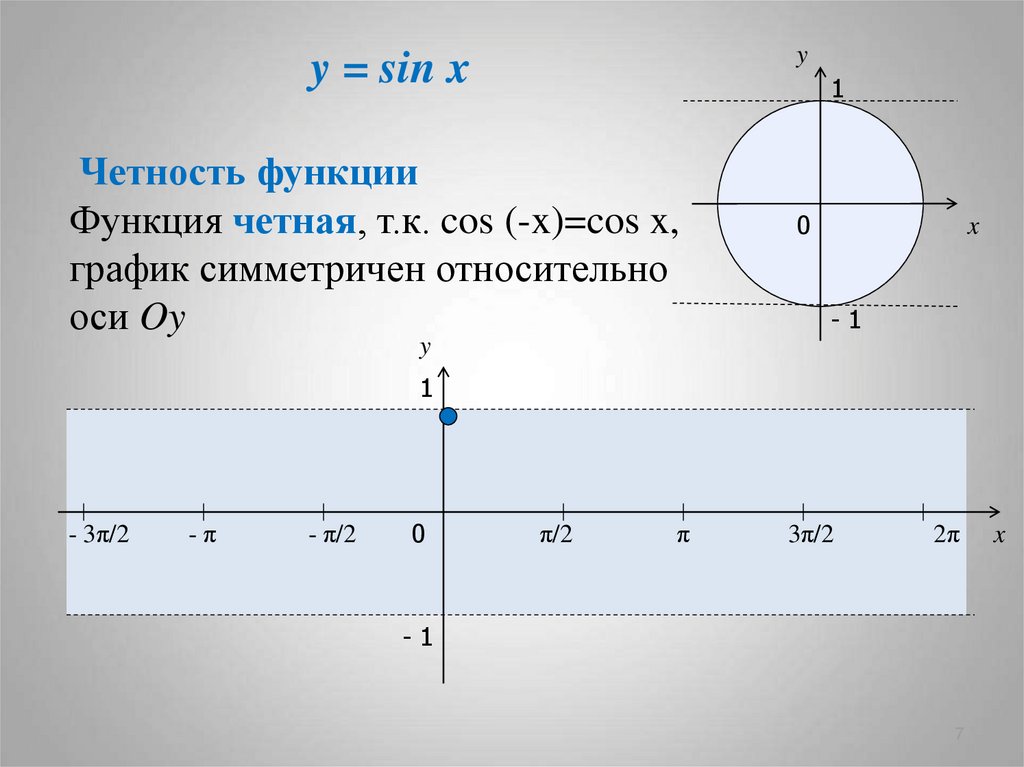
Четность функции
Функция четная, т.к. cos (-x)=cos x,
график симметричен относительно
оси Oy
0
x
-1
y
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
7
x
8. y = cos x
yy = cos x
1
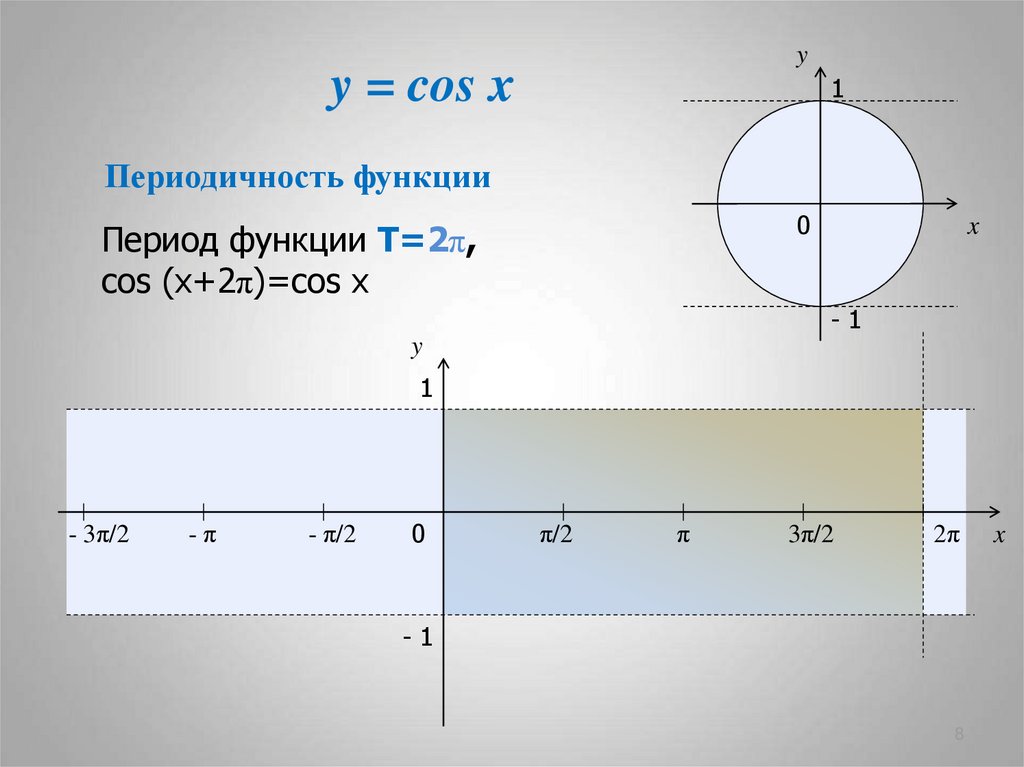
Периодичность функции
0
Период функции Т=2π,
cos (x+2π)=cos x
x
-1
y
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
8
x
9. y = cos x
yy = cos x
1
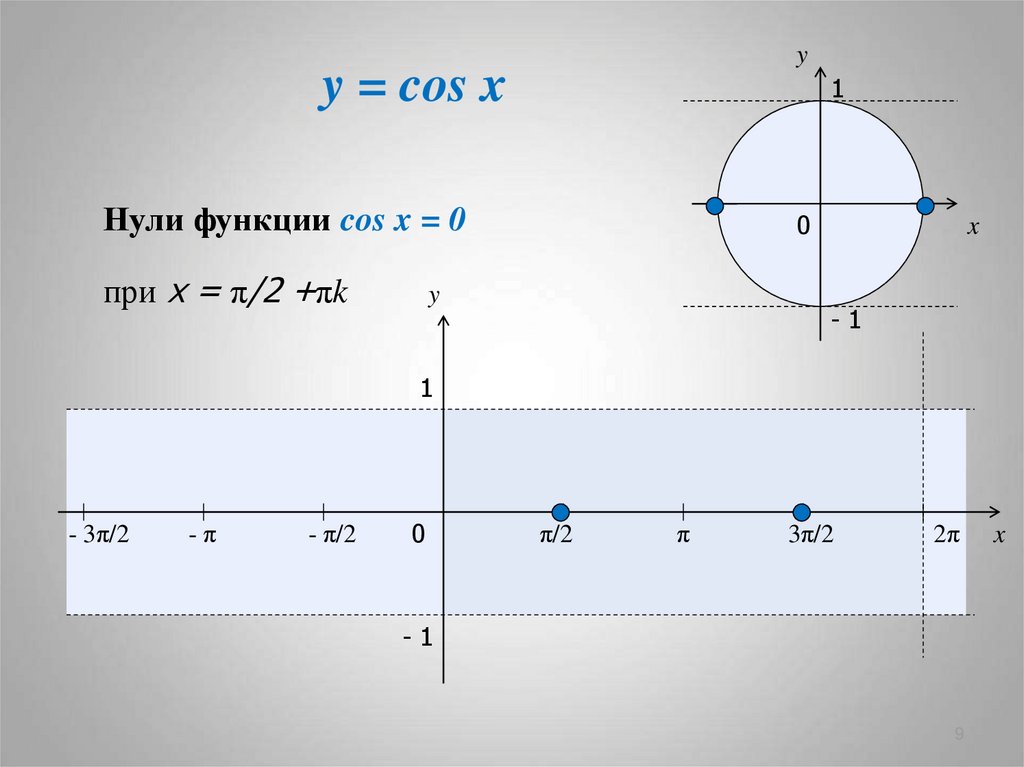
Нули функции cos x = 0
при x = π/2 +πk
0
y
x
-1
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
9
x
10. y = cos x
yy = cos x
1
-1
0
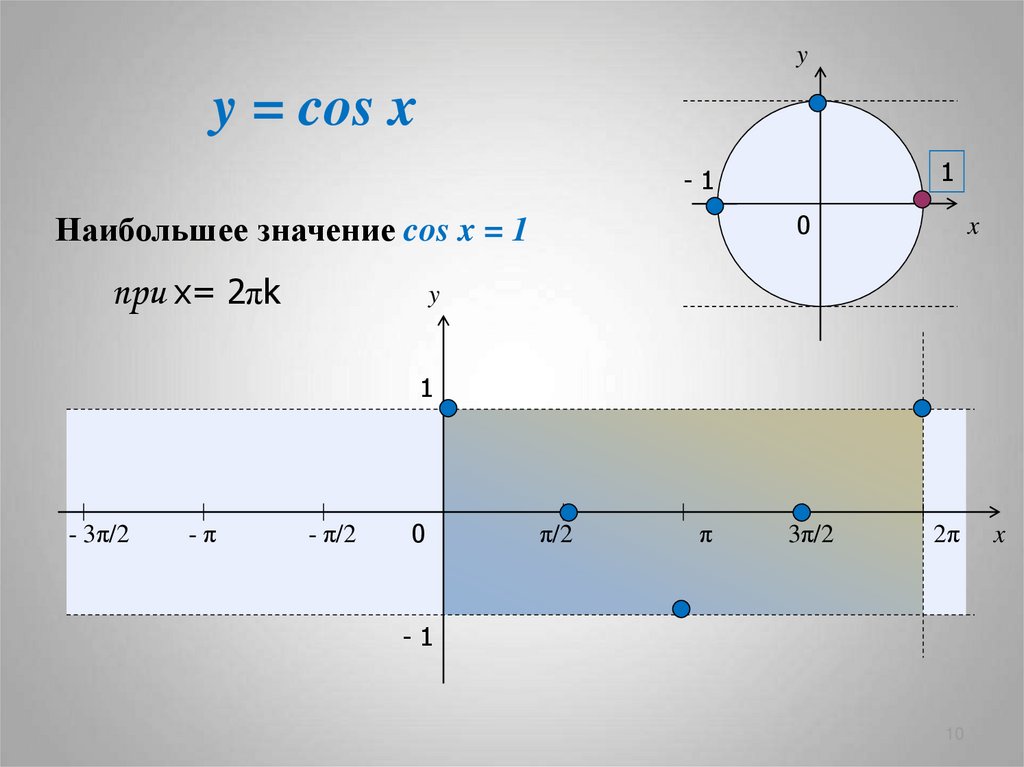
Наибольшее значение cos x = 1
при х= 2πk
x
y
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
10
x
11. y = cos x
yy = cos x
-1
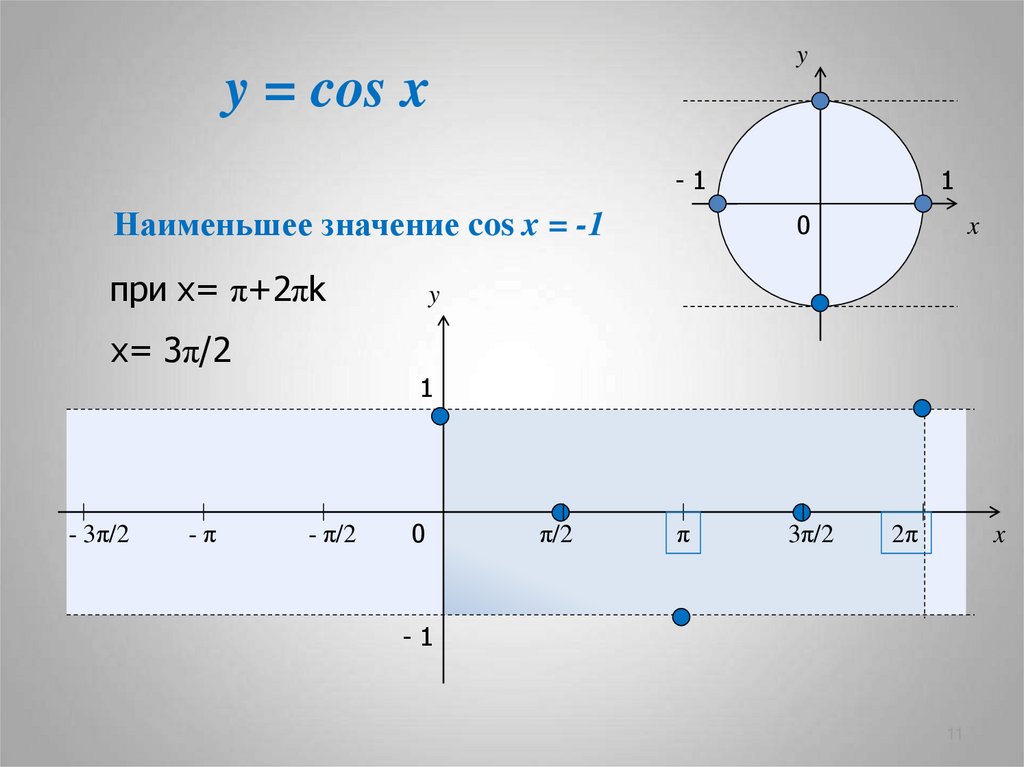
Наименьшее значение cos x = -1
при х= π+2πk
1
0
x
y
х= 3π/2
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
x
-1
11
12. y = cos на отрезке
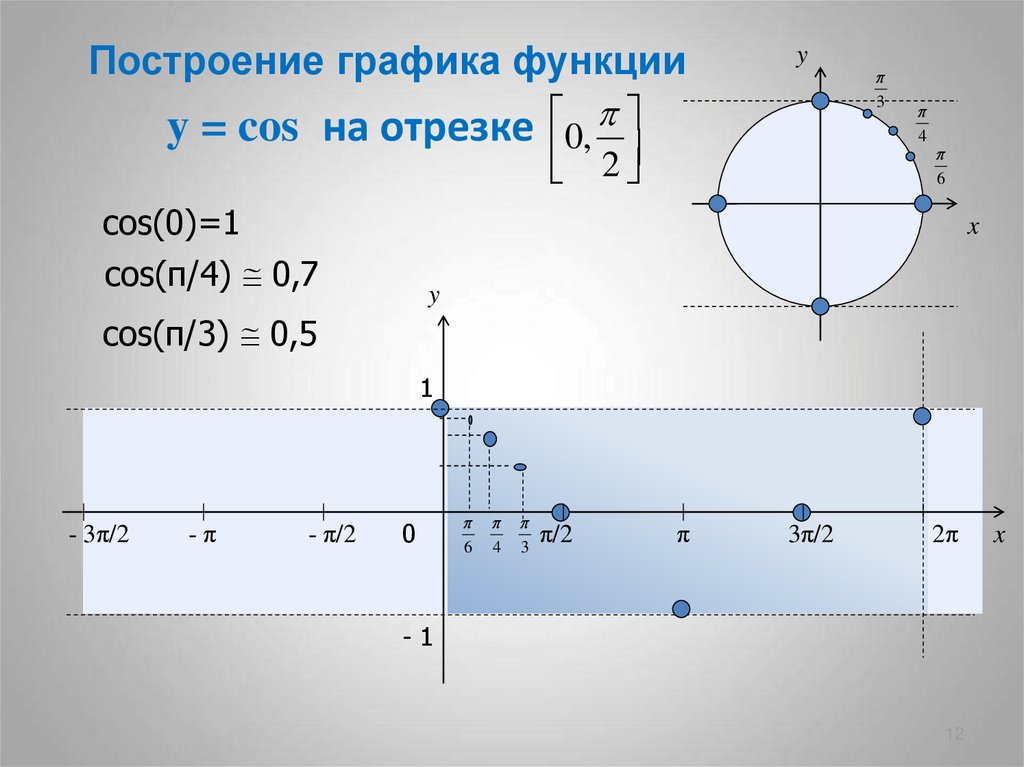
Построение графика функцииy = cos на отрезке
y
0, 2
3
4
6
cos(0)=1
x
cos(π/4) 0,7
y
cos(π/3) 0,5
1
- 3π/2
-π
- π/2
0
6 4 3
π/2
π
3π/2
2π
-1
12
x
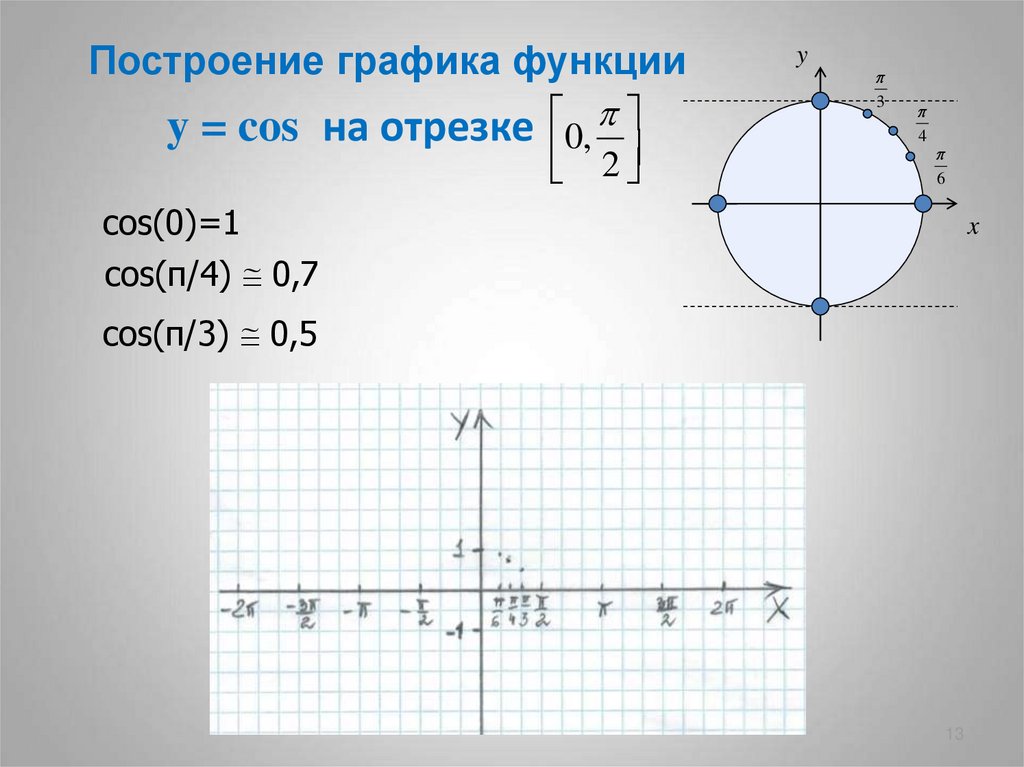
13. y = cos на отрезке
Построение графика функцииy = cos на отрезке
0, 2
y
3
4
6
cos(0)=1
x
cos(π/4) 0,7
cos(π/3) 0,5
13
14.
1415.
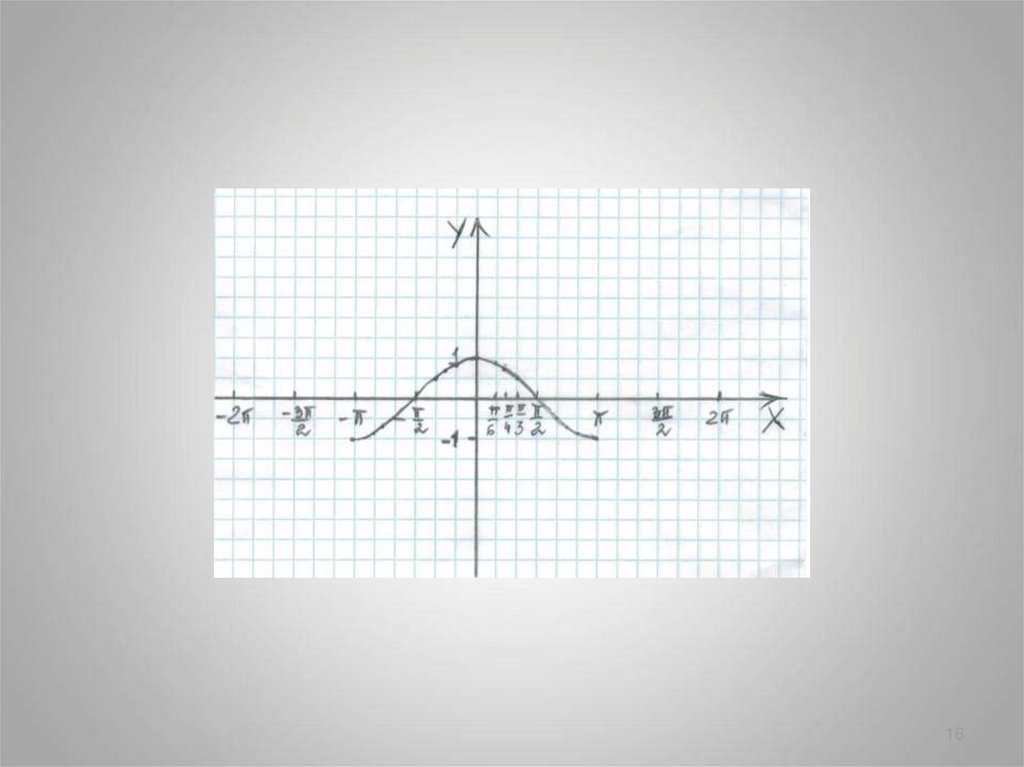
1516.
1617.
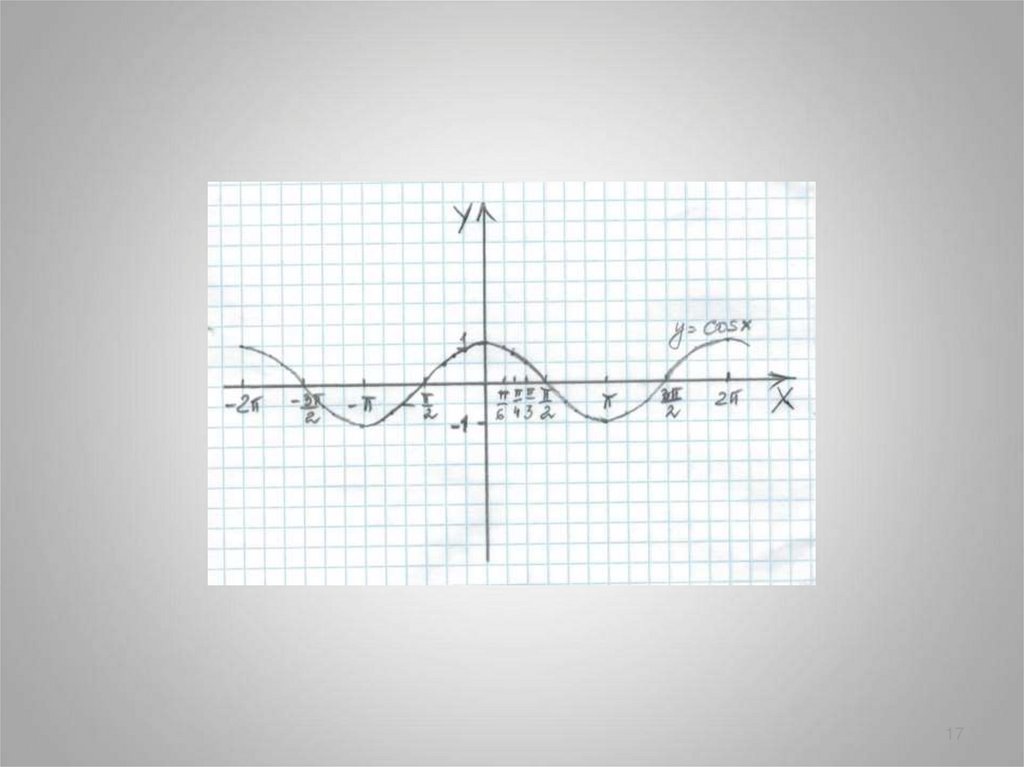
1718. y = cos x
График функции y=cos x называется синусоидаy
1
-2π
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
5π/2 x
-1
18
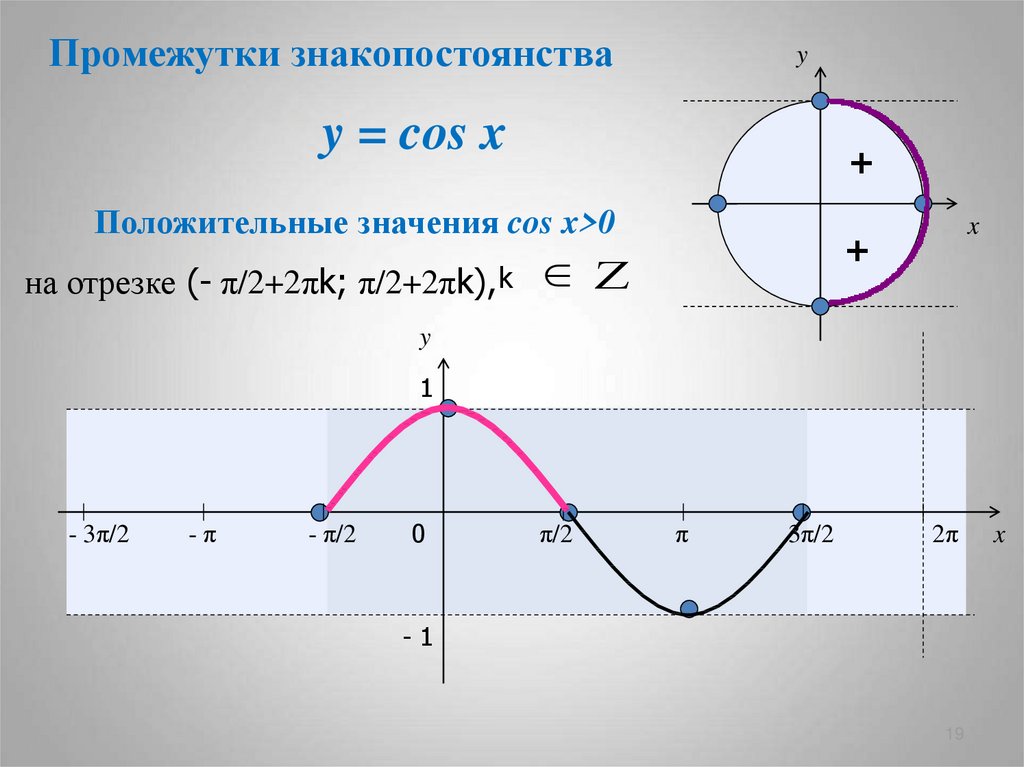
19. y = cos x
Промежутки знакопостоянстваy
y = cos x
+
Положительные значения cos x>0
на отрезке (- π/2+2πk; π/2+2πk), k
x
+
y
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
19
x
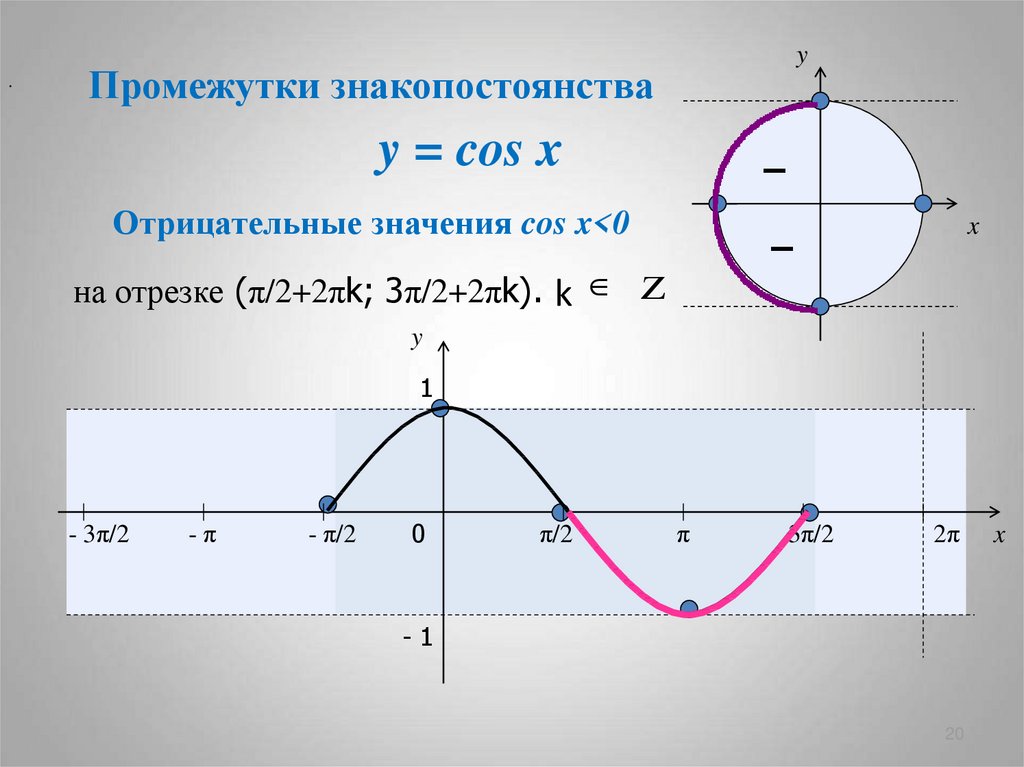
20. y = cos x
.y
Промежутки знакопостоянства
y = cos x
–
Отрицательные значения cos x<0
x
–
на отрезке (π/2+2πk; 3π/2+2πk). k
y
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
20
x
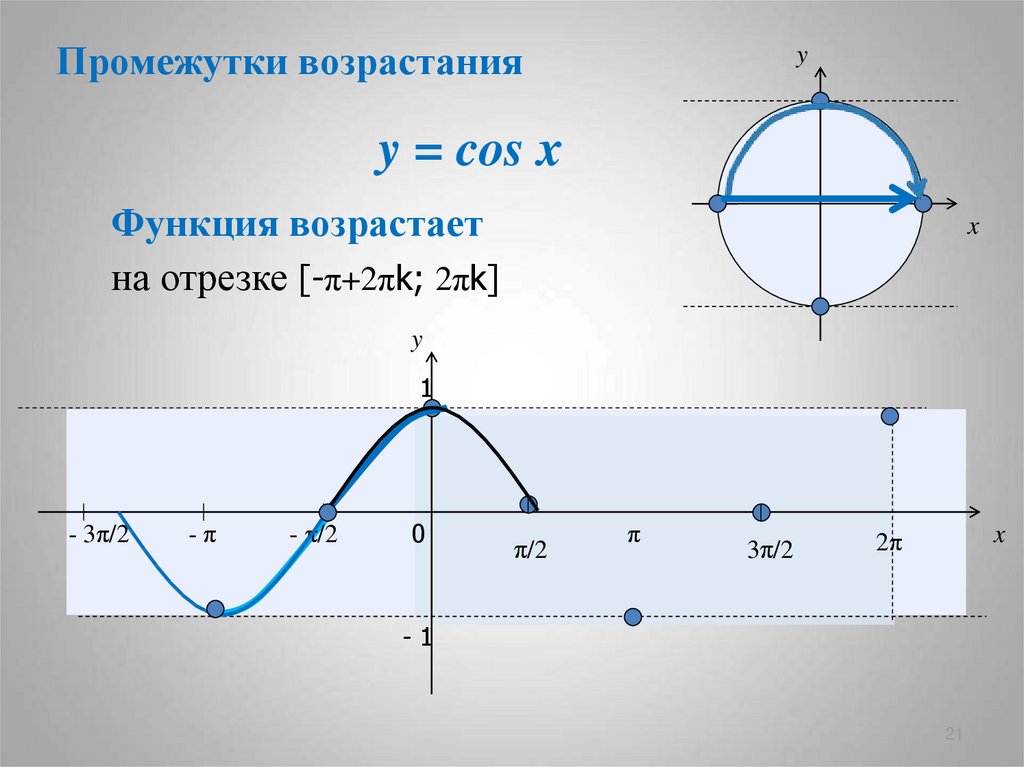
21. y = cos x
Промежутки возрастанияy
y = cos x
Функция возрастает
на отрезке [-π+2πk; 2πk]
x
y
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
x
2π
-1
21
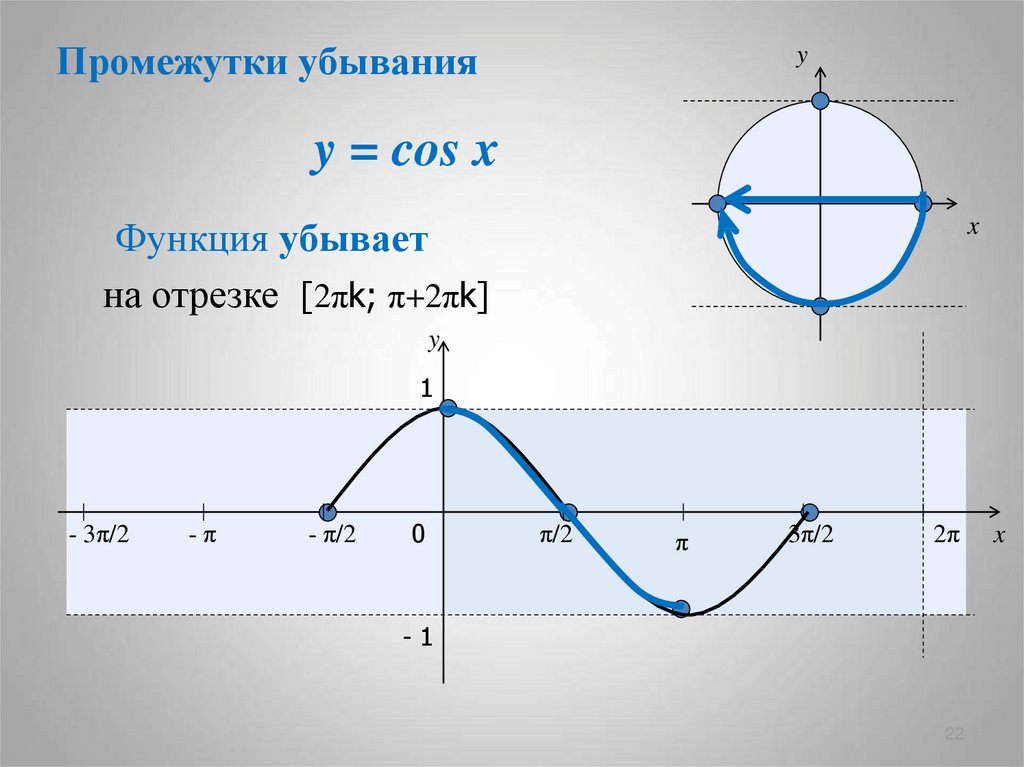
22. y = cos x
Промежутки убыванияy
y = cos x
Функция убывает
на отрезке [2πk; π+2πk]
x
y
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
22
x
23.
ЗадачаСравнить числа
Так как
= 3,14,
< 2 < 3 <
и
cos 3
1,57
, то
cos 2
2
2
Из графика видно, что на отрезке ;
2
функция у=cos х убывает.
Ответ: cos 2 > cos 3.
23
24. Упражнения
25.
Преобразование графикаСдвиг вдоль оси ординат
y = cos x
4,5
y = cos x + 3
4
Построить график 3,5
3
функции
2,5
3
2
у=cosх+3
1,5
y = cos x
1
+
0,5
вверх
0
2
-0,5
-1
-1,5
y = cos x
1,5
Построить график
функции
у=sinх-3
1
0,5
0
-0,5
-1
y = cosx - 3
-1,5
-2
-2,5
-3
-
-3,5
вниз
-3
-4
-4,5
25
26.
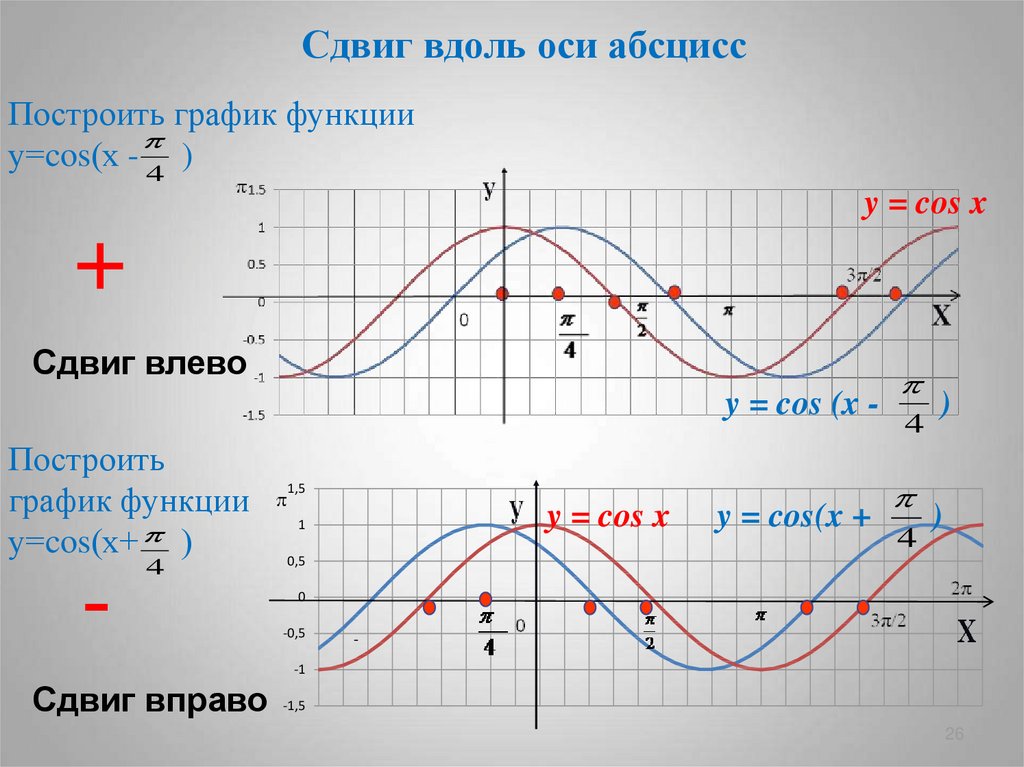
Сдвиг вдоль оси абсциссПостроить график функции
у=cos(х - 4 )
y = cos x
+
Сдвиг влево
y = cos (x Построить
график функции
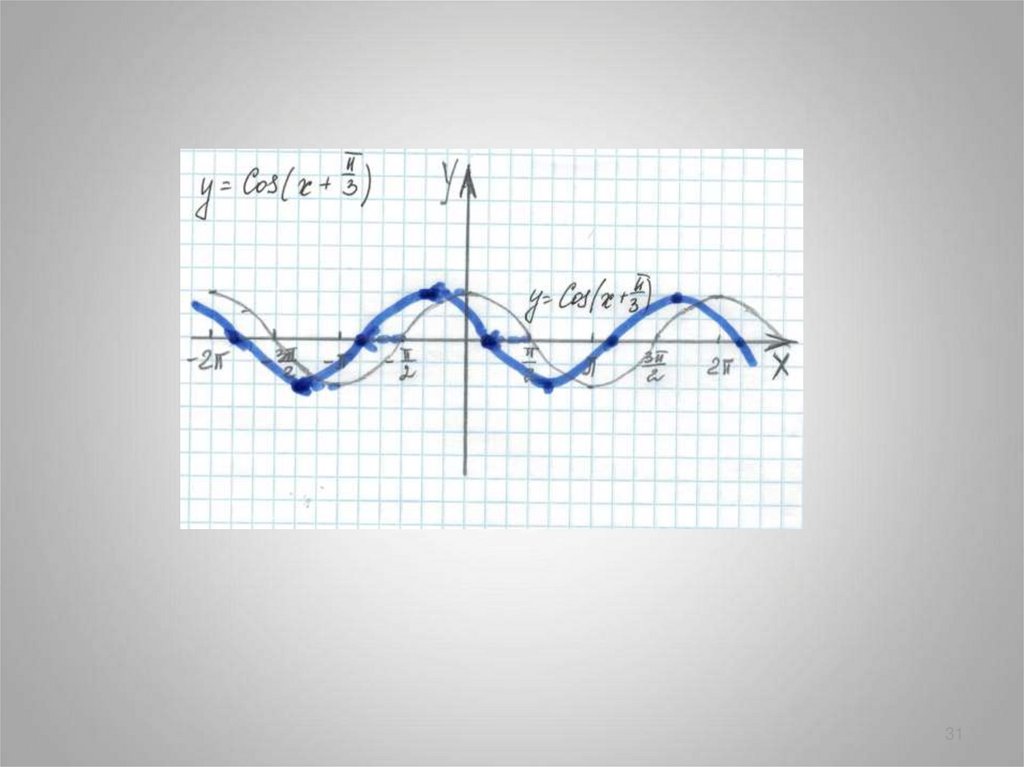
у=cos(х+ )
-
4
1,5
y = cos x
1
y = cos(x +
4
4
)
)
0,5
0
-0,5
-
-1
Сдвиг вправо
-1,5
26
27.
2728.
2829.
2930.
3031.
3132.
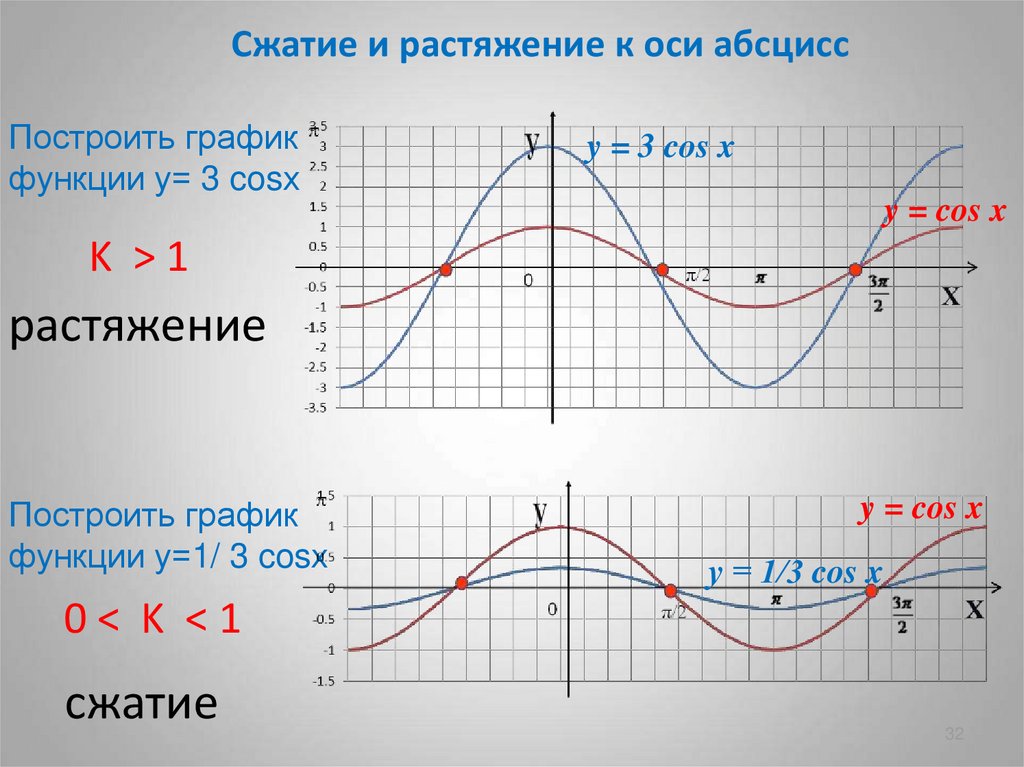
Сжатие и растяжение к оси абсциссПостроить график
функции у= 3 cosх
y = 3 cos x
y = cos x
K >1
растяжение
Построить график
функции у=1/ 3 cosх
y = cos x
у = 1/3 cos x
0< K <1
сжатие
32
33.
3334.
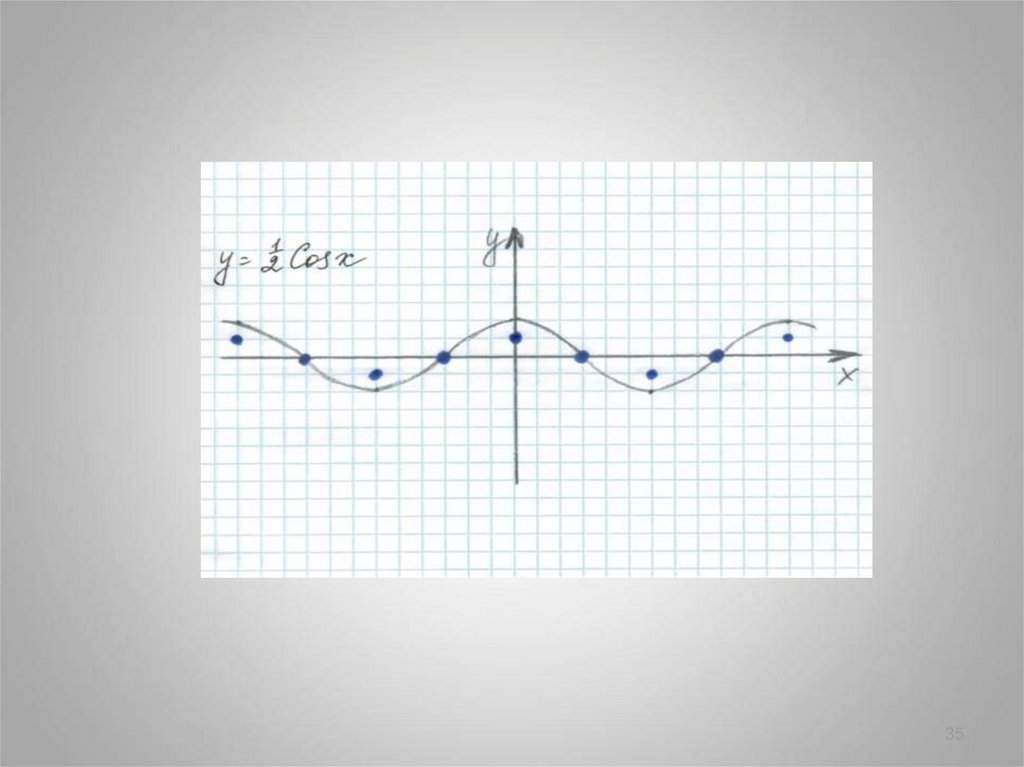
3435.
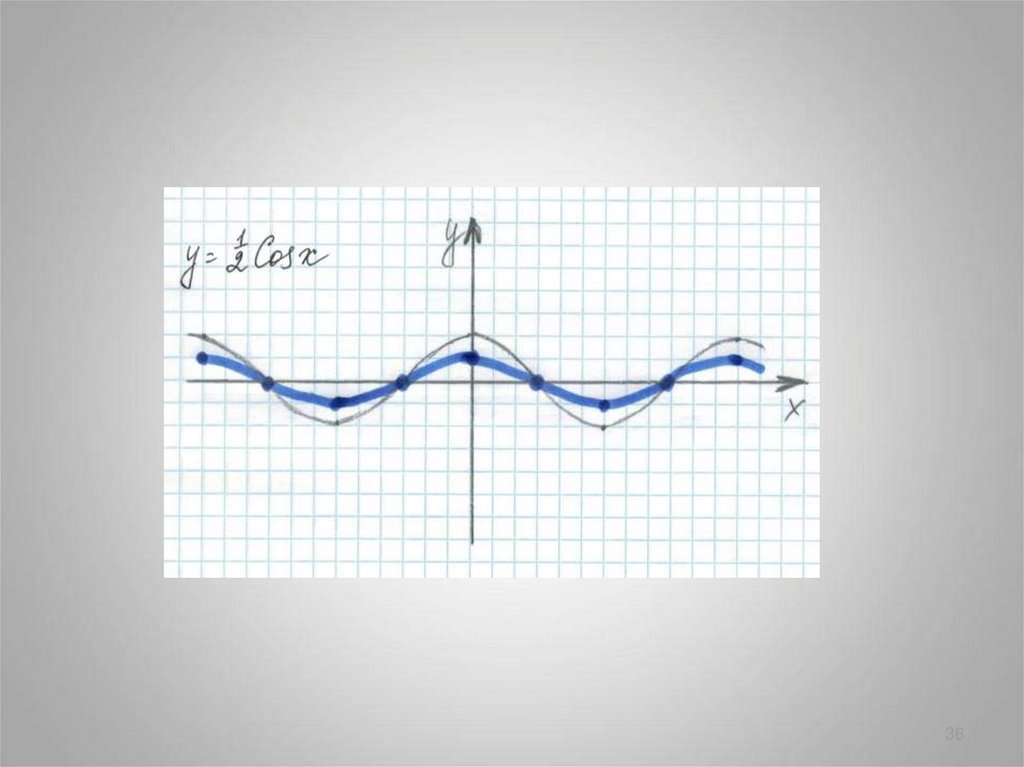
3536.
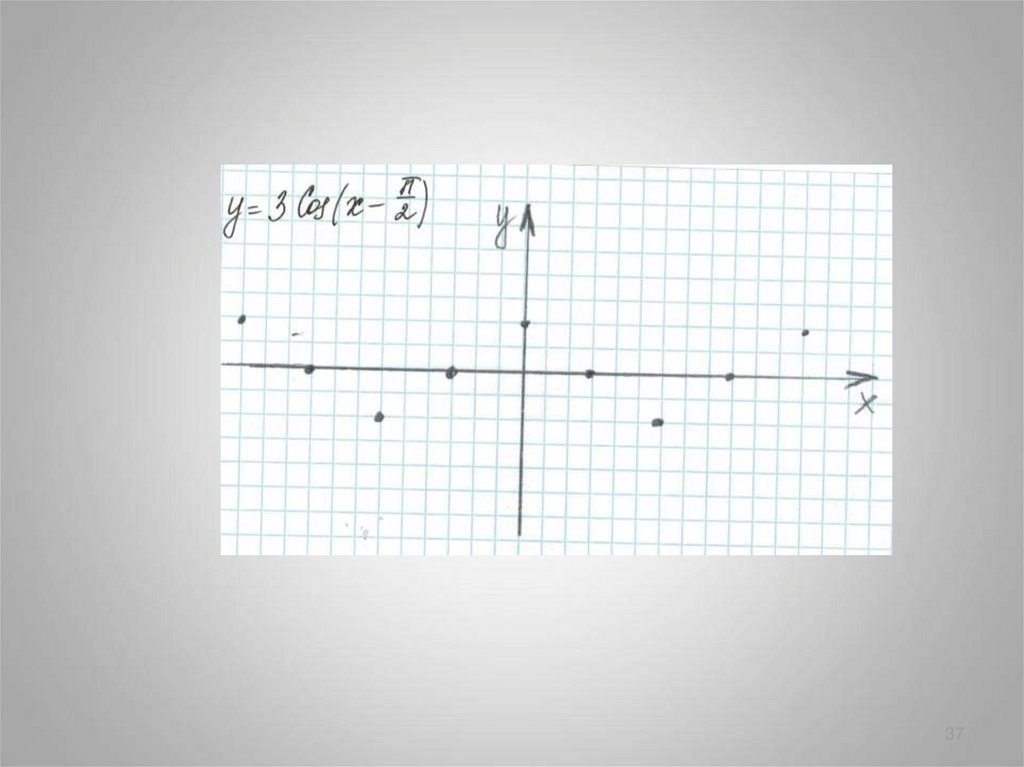
3637.
3738.
3839.
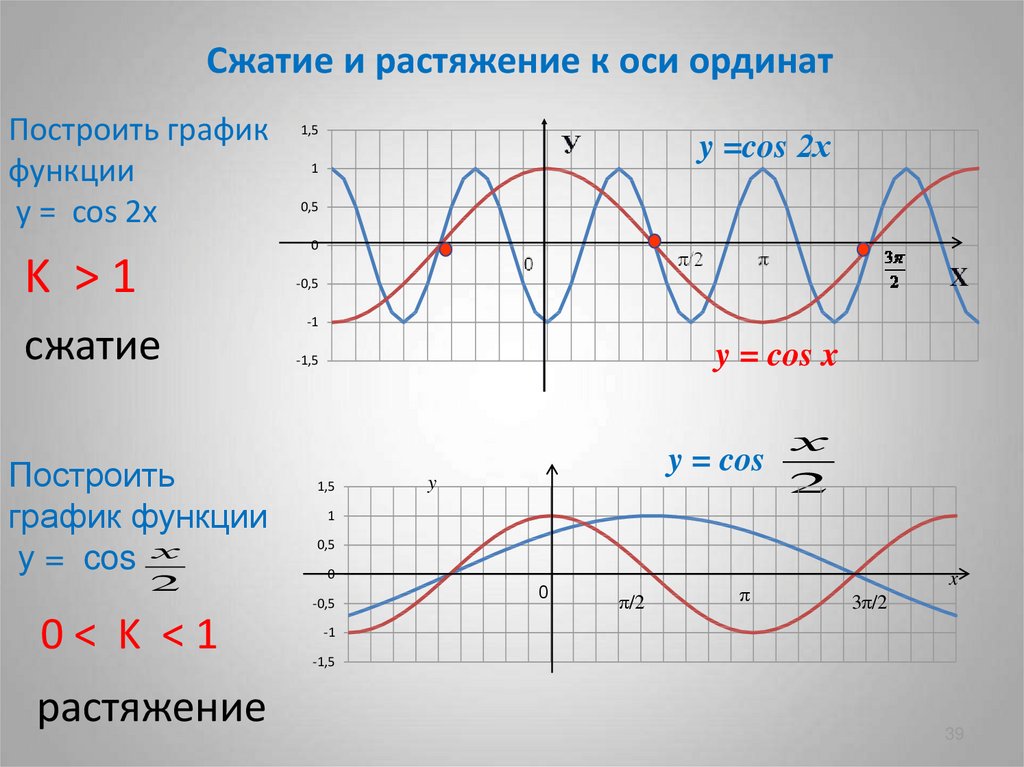
Сжатие и растяжение к оси ординатПостроить график
функции
у = cos 2х
1,5
y =cos 2х
1
0,5
0
K >1
-0,5
сжатие
Построить
график функции
у = cos х
2
-1
y = cos x
-1,5
1,5
растяжение
y
х
2
1
0,5
0
-0,5
0< K <1
y = cos
0
π/2
π
x
3π/2
-1
-1,5
39
40.
Уy = cos x
х
При каких значениях х функция у=cos x принимает
значение, равное 0? 1? -1?
Может ли функция у= cos x принимать значение
больше 1, меньше -1?
При каких значениях х функция у=cos x принимает
наибольшее (наименьшее) значение?
Каково множество значений функции у=cos x?
40
41. Список используемых источников
1. Алгебра и начала анализа. Учебник для 10–11классов, общеобразовательных учреждений.
А.Н. Колмогоров, А.М. Абрамов, и др…,
«Просвещение», М.: 2010 год.
41









 Математика
Математика