Похожие презентации:
Площадь криволинейной трапеции
1. Площадь криволинейной трапеции
2.
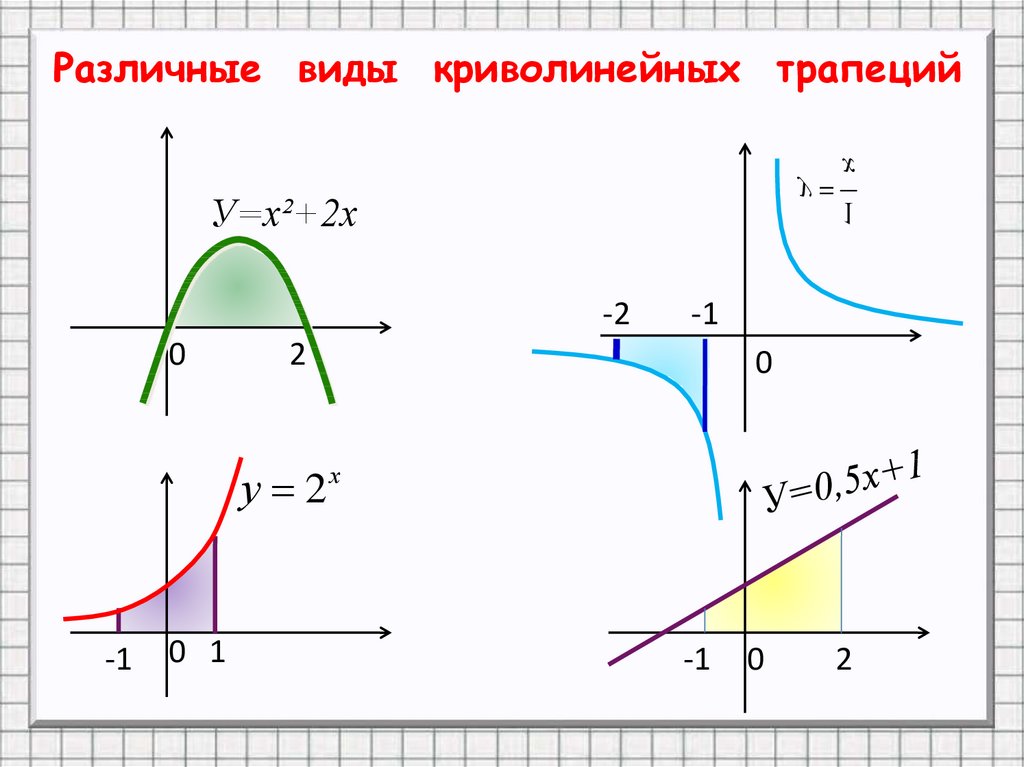
Различные виды криволинейных трапецийх
у
1
У=х²+2х
-2
0
2
у 2
-1
0 1
-1
0
х
-1
0
2
3.
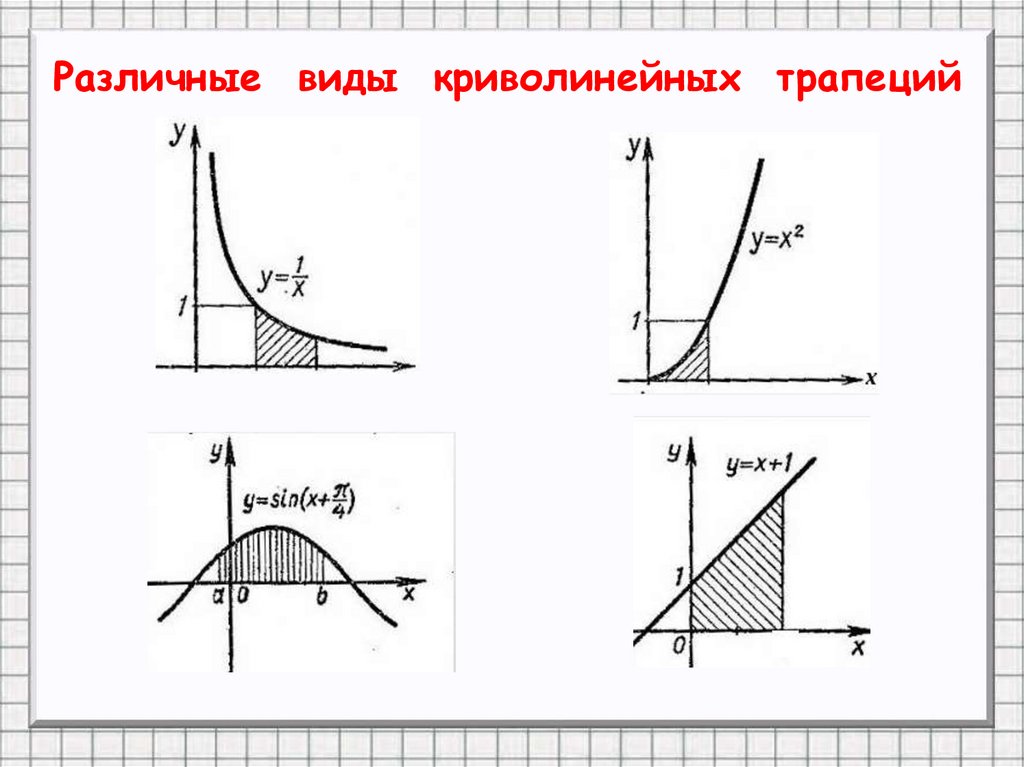
Различные виды криволинейных трапеций4.
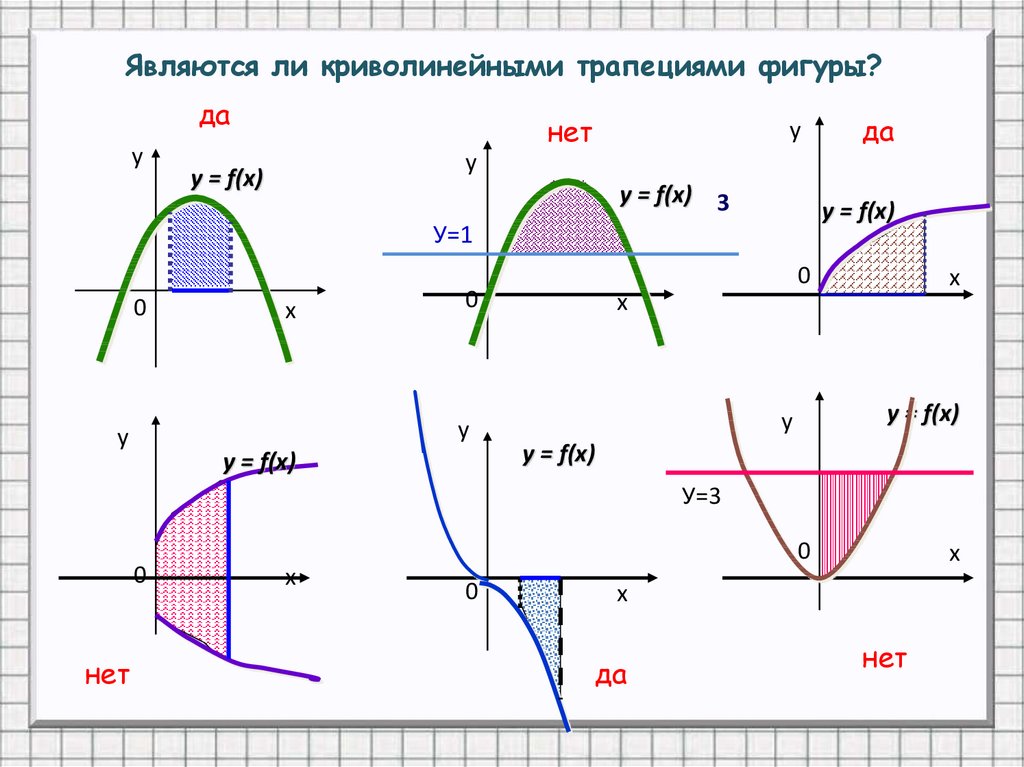
Являются ли криволинейными трапециями фигуры?да
у
нет
у
у
y = f(x)
y = f(x) 3
y = f(x)
У=1
0
х
0
0
у
у
да
y = f(x)
х
х
y = f(x)
у
y = f(x)
У=3
0
нет
0
х
0
х
х
да
нет
5.
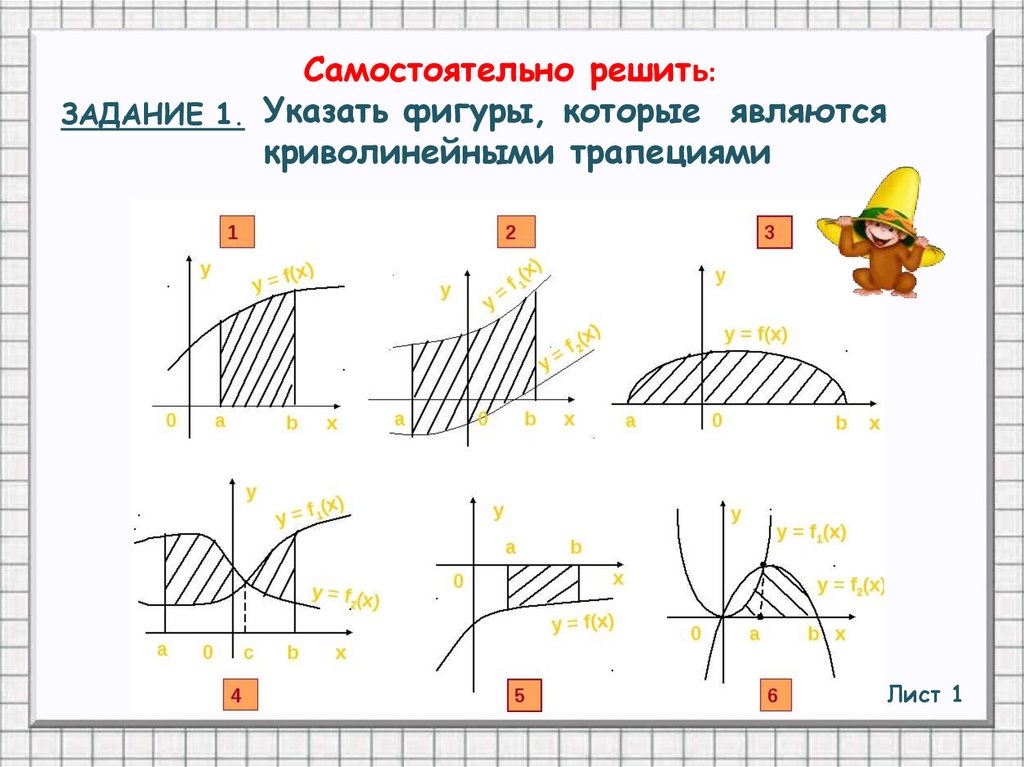
Самостоятельно решить:ЗАДАНИЕ 1. Указать фигуры, которые являются
криволинейными трапециями
Лист 1
6.
ЗАДАНИЕ 2. Указать фигуры, которые не являютсякриволинейными трапециями
Лист 2
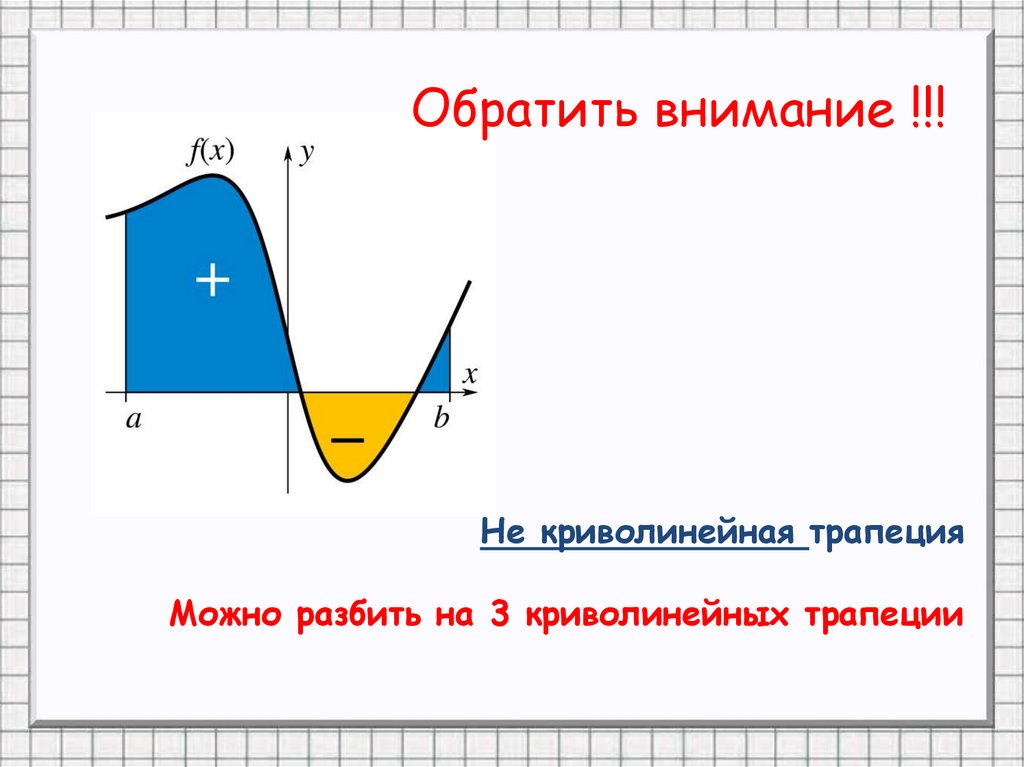
7. Обратить внимание !!!
Не криволинейная трапецияМожно разбить на 3 криволинейных трапеции
8.
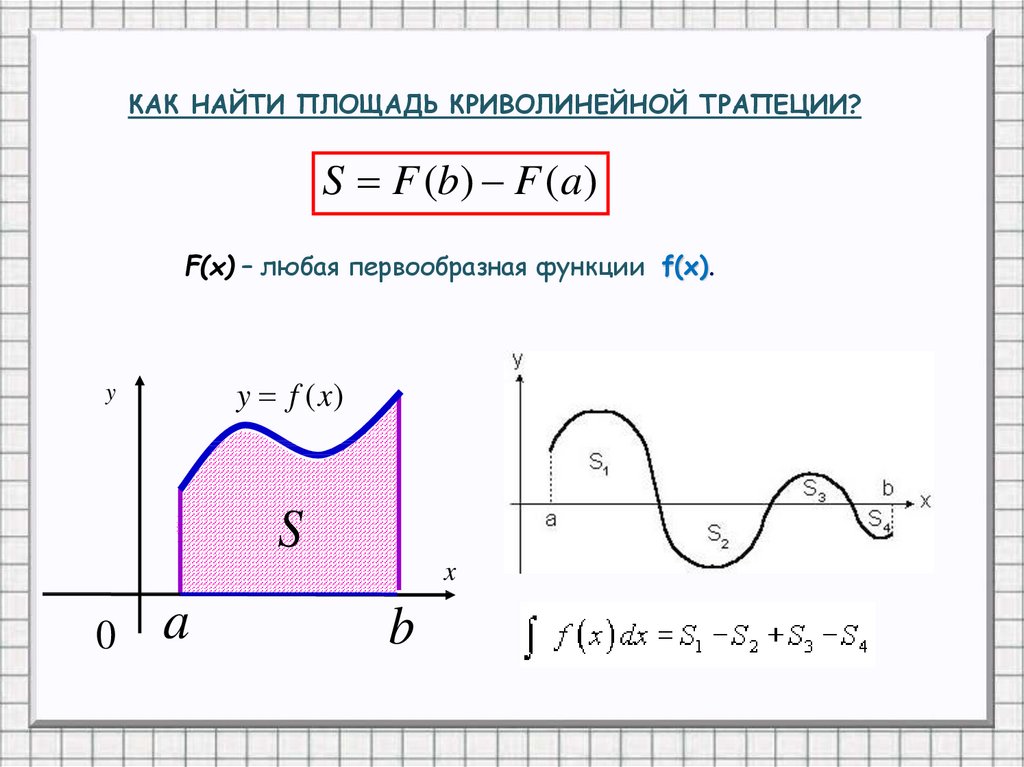
КАК НАЙТИ ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ?S F (b) F (a)
F(x) – любая первообразная функции f(x).
y f (x)
y
S
x
0
a
b
9.
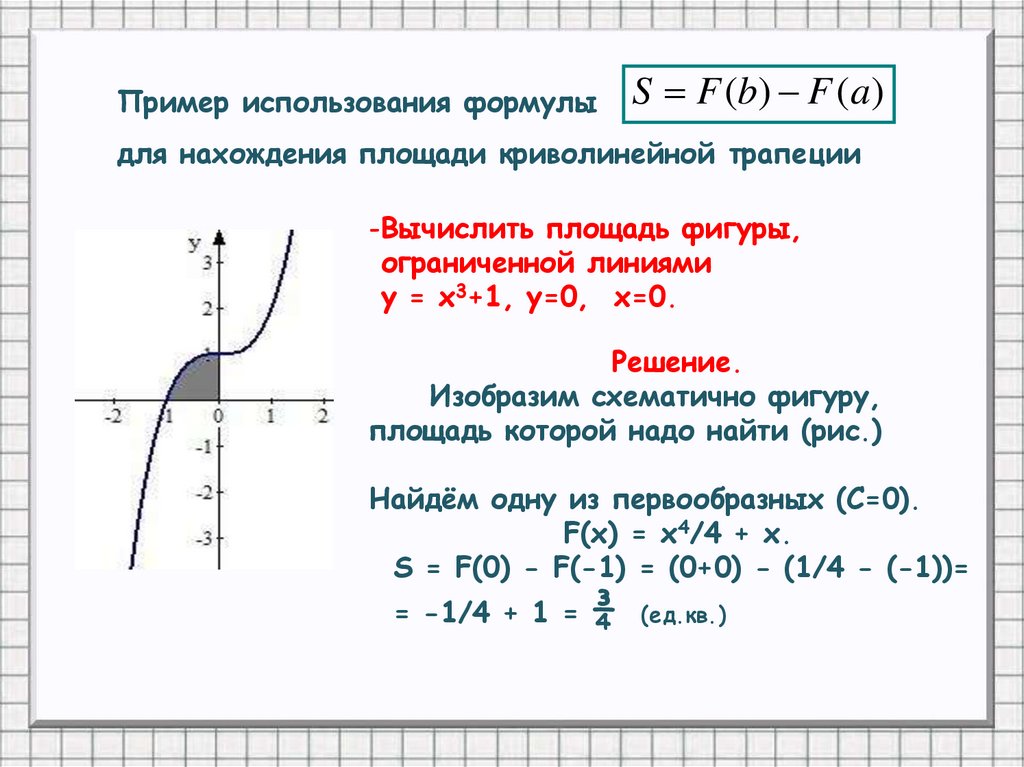
Пример использования формулыS F (b) F (a)
для нахождения площади криволинейной трапеции
-Вычислить площадь фигуры,
ограниченной линиями
у = x3+1, у=0, x=0.
Решение.
Изобразим схематично фигуру,
площадь которой надо найти (рис.)
Найдём одну из первообразных (С=0).
F(x) = x4/4 + x.
S = F(0) - F(-1) = (0+0) - (1/4 - (-1))=
= -1/4 + 1 =
¾
(ед.кв.)
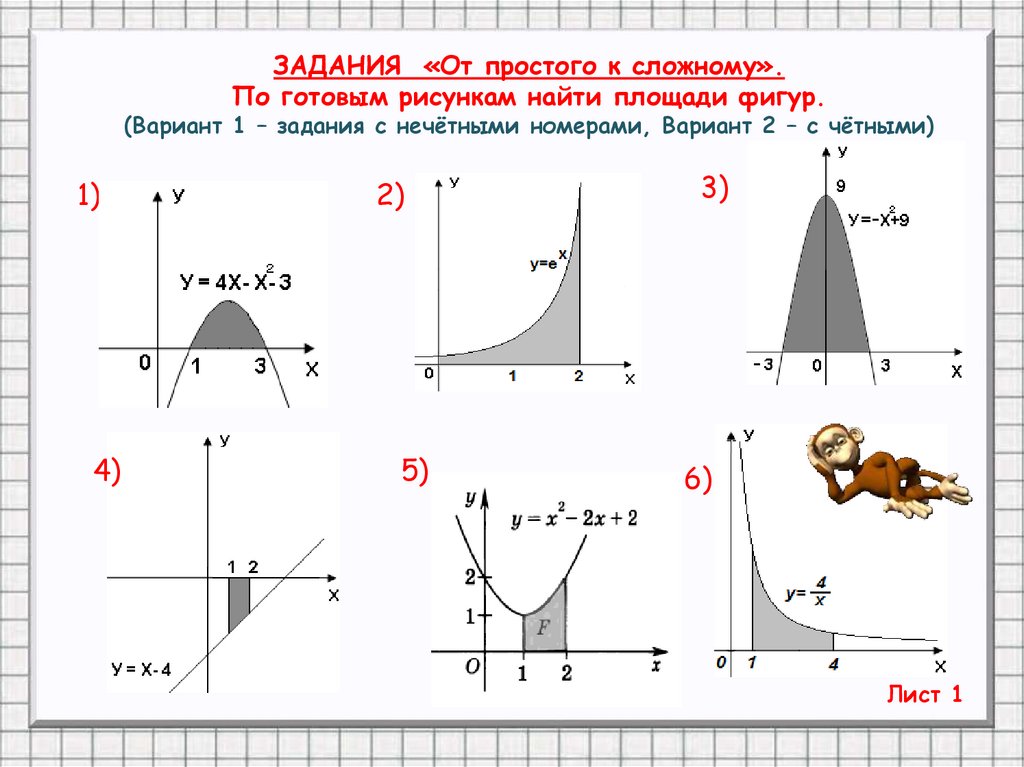
10. ЗАДАНИЯ «От простого к сложному». По готовым рисункам найти площади фигур. (Вариант 1 – задания с нечётными номерами, Вариант 2
– с чётными)1)
4)
2)
5)
3)
6)
Лист 1
11.
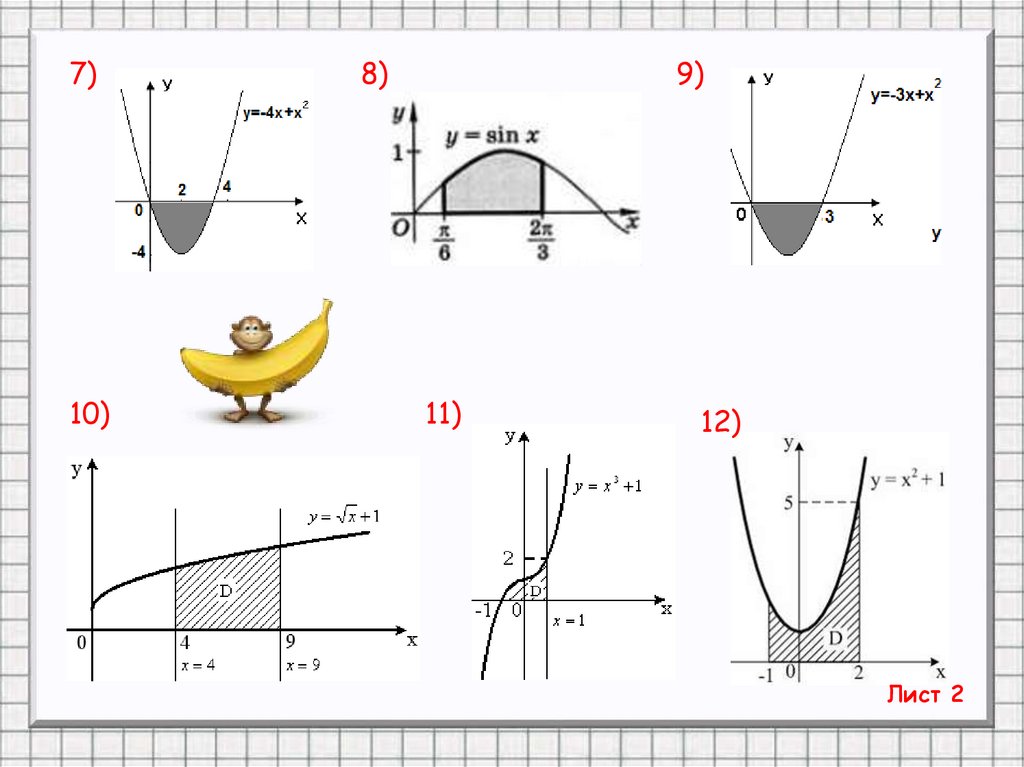
7)10)
8)
9)
11)
12)
Лист 2
12.
13)16)
14)
17)
15)
18)
Лист 3
13.
ДОМАШНЕЕ ЗАДАНИЕПодготовить информацию
- об истории возникновения определённого интеграла;
- о сферах его применения.




 Математика
Математика








