Обобщенный алгоритм анализа иерархии

1.

Обобщенный алгоритм анализа иерархии
1. Построение дерева целей;
2. Оценка важности компонентов
каждого узла дерева целей;
3. Оценка важности выявленных задач
вне дерева целей.
Метод анализа иерархий

2.

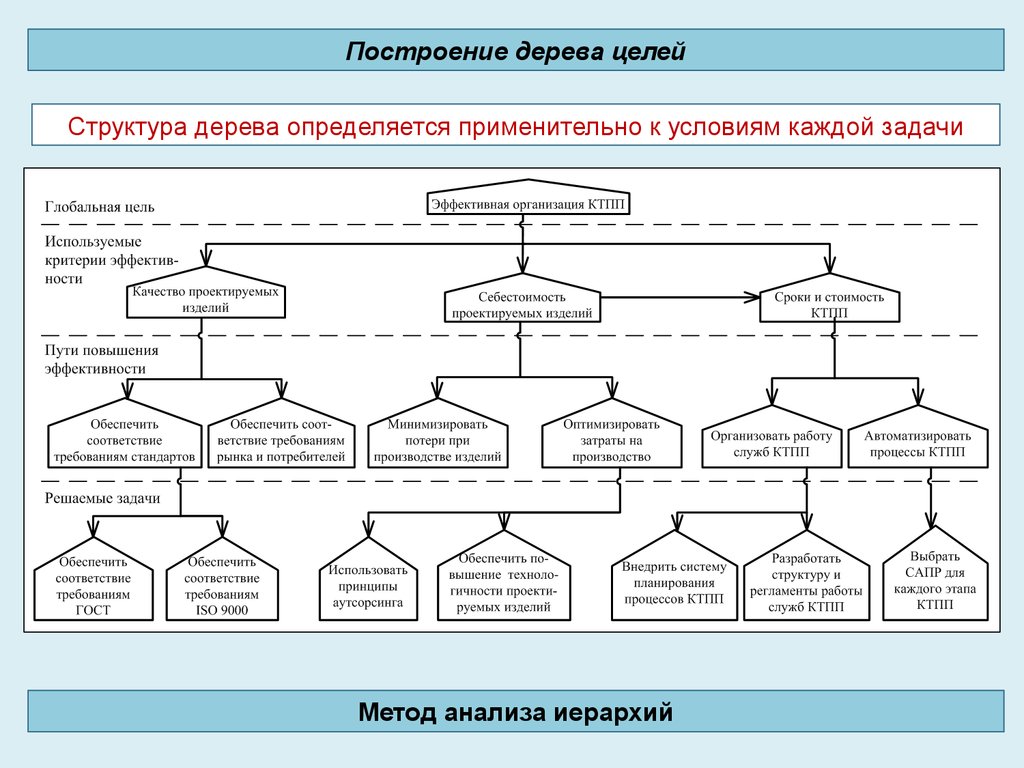
Построение дерева целей
Структура дерева определяется применительно к условиям каждой задачи
Метод анализа иерархий

3.

Оценка важности компонентов узла
Для каждого узла дерева нужно заполнить матрицу парных сравнений
Узелk
Ek1
E k2
k
Е
k
[E ] =
Е
Е
Е
k
k
1
1
2
k
Е
…
…
k
k
nk
1
Е
21
nk1
…
Ekn
k
Е 2
k
Е 12
1
…
k
Е nk2
Метод анализа иерархий
…
…
…
…
…
k
Е nk
k
Е 1nk
k
Е 2nk
…
1

4.

Заполнение матрицы парных сравнений
Матрица парных сравнений для каждого узла m
E km – квадратная матрица размерности n n с единичной диагональю
Если Цkm,i доминирует над Цkm,j , то vkm, i,j = p (степень значимости), а vkm, j,i = 1/p
Если Цkm,i и Цkm,j равно предпочтительны, то vkm, i,j = vkm, j,i = 1.
Цkm,1
Цkm,1
1
Цkm,2
vkm, 2,1
Цkm,3
vkm, 3,1
…
Цkm,n
…
vkm, n,1
Цkm,2
vkm, 1,2
1
vkm, 3,2
…
vkm, n,2
Цkm,3
…
Цkm,n
vkm, 1,3
… vkm, 1,n
vkm, 2,3
… vkm, 2,n
1
…
vkm, n,3
vkm, 3,n
…
…
…
1
Метод анализа иерархий
Пример
k = 2 – уровень дерева целей
m = 1 – узел дерева целей
n = 3 – количество целей
E 21
Ц21,1
Ц21,2
Ц21,3
Ц21,1
1
8
0,250
Ц21,2
0,125
1
0,333
Ц21,3
4
3
1

5.

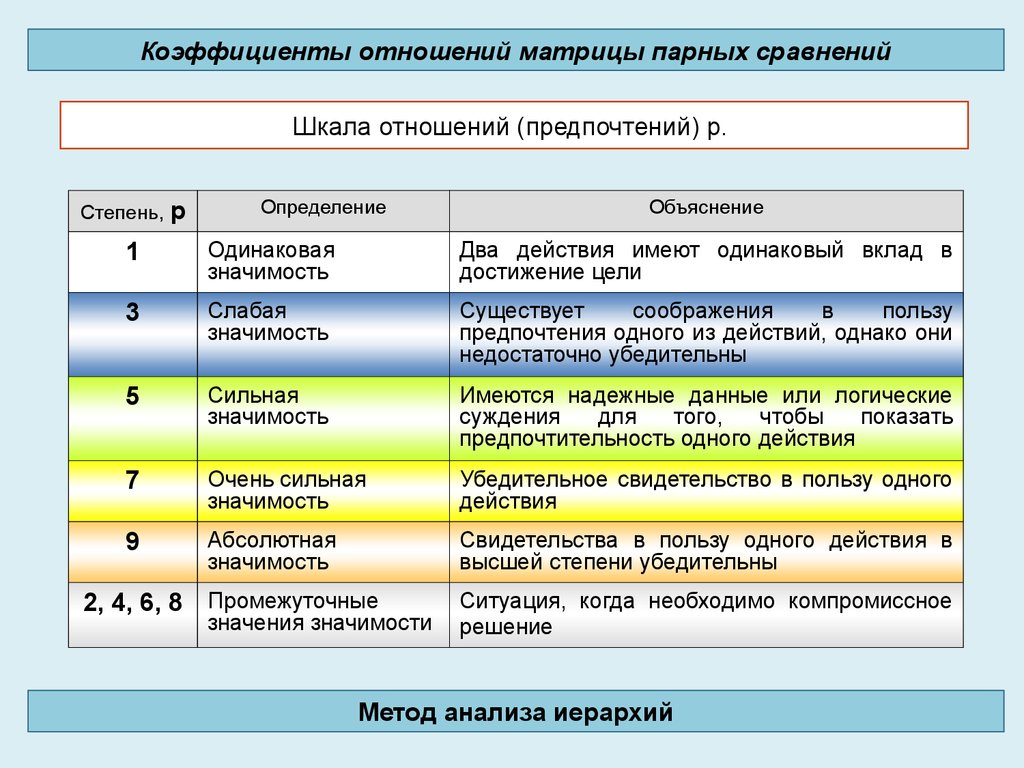
Коэффициенты отношений матрицы парных сравнений
Шкала отношений (предпочтений) p.
Степень, p
Определение
Объяснение
1
Одинаковая
значимость
Два действия имеют одинаковый вклад в
достижение цели
3
Слабая
значимость
Существует
соображения
в
пользу
предпочтения одного из действий, однако они
недостаточно убедительны
5
Сильная
значимость
Имеются надежные данные или логические
суждения
для
того,
чтобы
показать
предпочтительность одного действия
7
Очень сильная
значимость
Убедительное свидетельство в пользу одного
действия
9
Абсолютная
значимость
Свидетельства в пользу одного действия в
высшей степени убедительны
2, 4, 6, 8 Промежуточные
значения значимости
Ситуация, когда необходимо компромиссное
решение
Метод анализа иерархий

6.

Оценка компонентов узла.
Далее для каждой матрицы необходимо рассчитать W, λmax, OC
/
Если ОС<0,1, то суждения эксперта логичны; если 0,1<ОС<0,2, то суждения
сомнительны; в противном случае – эксперт нелогичен в своих суждениях.
Метод анализа иерархий

7.

Оценка важности задач в простых деревьях. Методика PATTERN
В простых деревьях важность задачи можно рассчитать как произведение
весовых коэффициентов по пути от «корня» дерева к «листу»
w1
w11
w111
Цель1
Цель11
Цель111
Глобальная
цель
w21
w12
Цель12
Цель2
w22
Цель21
w112
w1 + w2= 1
w11 + w12= 1
w111 + w112= 1
w21 + w22 + w23= 1
w2
w23
Цель23
Цель22
Цель112
w*111= w1 w11 w111
w*112= w1 w11 w112
w*12= w1 w12
w*21= w2 w21
w*22= w2 w22
w*23= w2 w23
Метод анализа иерархий

8.

Оценка важности задач в сложных деревьях. Алгоритм нормализации
Для сложных деревьев, в которых к одному «листу» может вести несколько
путей требуется нормализация дерева
Нормализация графа
0
0,2
0,5
0,3
A
0,25
B
0,2
0,15
0,55
A1
1.
A2
B1
0,5
0,5
A21
A22
0,2
C
0,8
B21
0,6
0,85
B2
0,3
2.
3.
0,4
0,3
0,7
B22
C1
0,2
C11
C2
0,5
C12
Метод анализа иерархий
Дуги должны идти только
вниз;
Дуги должны идти только
на следующий уровень;
Все пути должны быть
одинаковой длины.

9.

Оценка важности задач в сложных деревьях. Нормализация направлений
0
0,2
0,25
A1
A2
0,5
A21
0,55
B
0,2
B1
B21
C
0,15
0,2
0,5
0,8
A22
0,5
0,3
A
Необходимо обеспечить,
чтобы в дереве
все связи вели на более низкие уровни
0,85
B2
0,3
0,4
0,3
0,6
C1
0,7 0,2
B22
C11
C2
0,5
C12
Метод анализа иерархий

10.

Оценка важности задач в сложных деревьях. Нормализация уровней
0,2
A
0,25
A1
0,5
A21
0
0,3
0,2
0,5
A22
0,15
B1
0,8
B21’
1
B21
0,5
B
0,2
0,55
A2
Необходимо обеспечить, чтобы в дереве
все связи вели только на следующий
уровень
C
0,85
0,4
C1
B2’
1
0,3
0,2
C11
B2
0,3
Эквивалентные связи
0,6
C2
0,5
C12
0,7
X
1
X
w
X
1
B22
Метод анализа иерархий
Y

11.

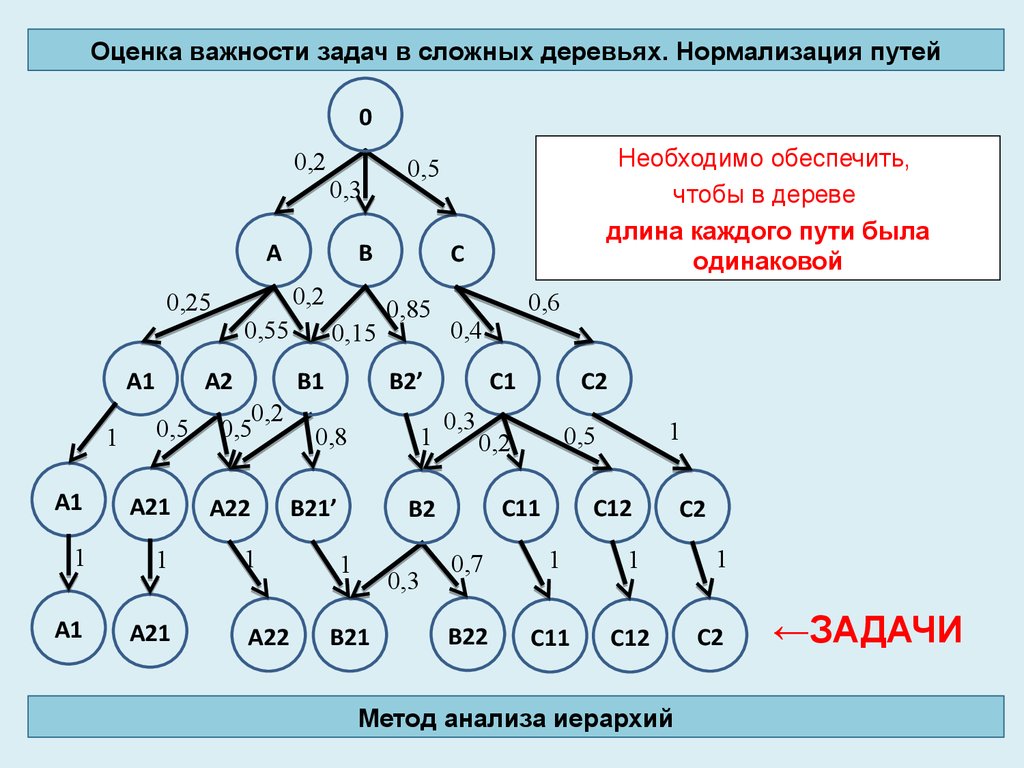
Оценка важности задач в сложных деревьях. Нормализация путей
0
0,2
0,3
A
A1
1
0,55
A2
0,5
B
0,2
0,25
0,15
B1
0,2
0,5
A1
A21
A22
1
1
1
A1
A21
A22
Необходимо обеспечить,
чтобы в дереве
длина каждого пути была
одинаковой
0,5
C
0,85
0,4
C1
B2’
0,8
1
B21’
0,3
0,3
B21
C2
1
0,5
0,2
C11
B2
1
0,6
C12
0,7
1
1
B22
C11
C12
Метод анализа иерархий
C2
1
C2
←ЗАДАЧИ

12.

Оценка важности задач в сложных деревьях. Построение матриц
Далее строятся матрицы, определяющие важность межуровневых связей
0
M01
1
M12
2
M23
AB1
B C1
CC2
A1 A21A1
A22A2
B21'
B2B2'
C11
C12
C2
A1 1 A1
0 10A100,25
0 00 0 00 000 00
A21 0A21
1 00A20,5
0A 000,200 000 00
0,55
A22 0A22
0 M
1 =0,50 0,20 00 00 00
M
=
0
B 0,3
B1 0,2
0,15 0
12 01
M34= B21 0 0 0
0,3 0 0 0
M23= B21' 0 B2'01C
0,5
00,8
0,85
0 00 0
B22 0 0 0
0 0,7 0 0 0
0,4
B2 0 C100 0 00 011 0,3
0
C11 0 0 0
0 0
0,6
C12 0C11
0 00C200 0 00 00 0,2
1 00
C2 0C12
0 00 00 00 00 0,50 01
C2 0
3
4
Метод анализа иерархий
0
0
0
0
1

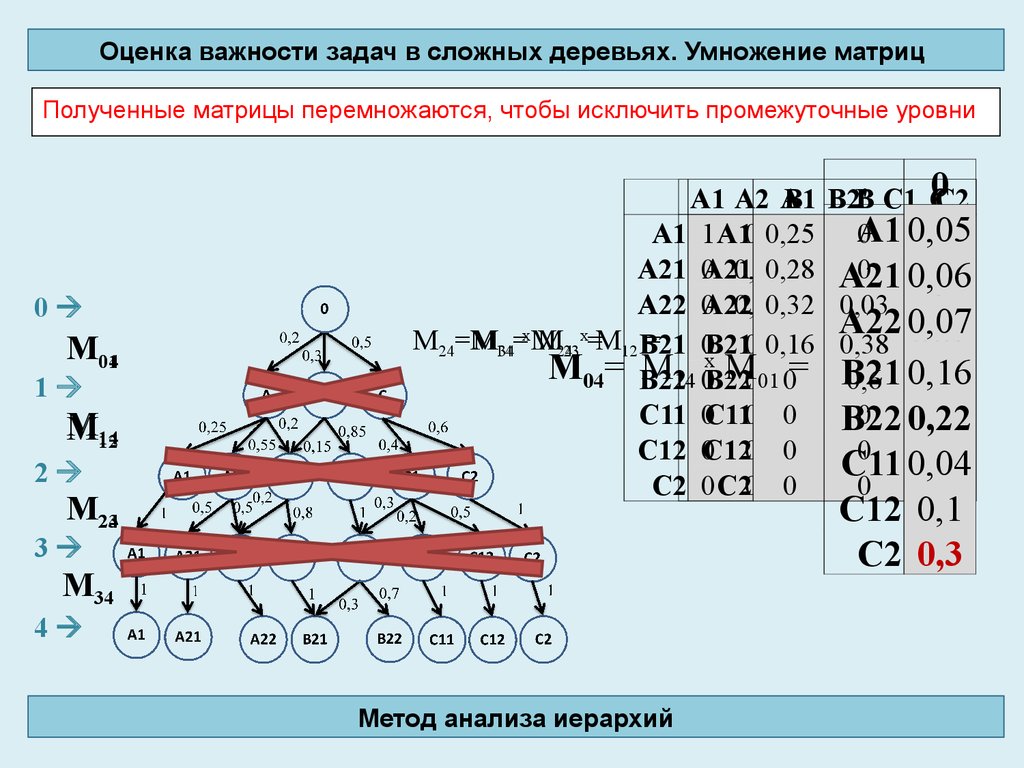
13.

Оценка важности задач в сложных деревьях. Умножение матриц
Полученные матрицы перемножаются, чтобы исключить промежуточные уровни
0
M04
01
1
M14
12
2
M24
23
A1 A2 A
B1
A1 1 A10 0,25
0
A21 0A21
0,50,28
0
A22 0A22
0,50,32
0,2
x
M24=M
M1434=M
M2423x=M12 B21
= 0B210 0,16
0,8
x
M04= B22
M14 0B22
M001 0=0
C11 0C110 00
C12 0C120 00
C2 0 C20 00
3
M34
4
Метод анализа иерархий
0C2
B2'B C1 C
0 A1
0 00,05
00
0 0 00,06
00
A21
0,03
0 0 00
A22 0,07
0,3
0,38
0,090,04
0
B21
0,16
0,7
0,60,21
0,08
0
0B22
0 0,20,22
0,08
0
0 0 0,5 0,20
C11 0,04
0 0 0 0,61
C12 0,1
C2 0,3