Похожие презентации:
Правила вычисления производных
1.
Правила вычисленияпроизводных
2.
Определение :• Функцию, имеющую производную
в точке х0 называют
дифференцируемой в точке х0
3.
Выучить :(х)' = 1,
С' = 0
С – соnst
( постоянное число)
(5)' = 0; (25)' = 0; (207)' = 0
4.
Правило 1• Если функции U и V
дифференцируемы в точке х0, то их
сумма дифференцируема в этой
точке и:
1.(U V ) U V
5.
Правило 2• Если функции U и V
дифференцируемы в точке х0,то их
произведение дифференцируемо в
этой точке и:
2.(U V ) U V U V
6.
Правило 3• Если функции U дифференцируема в
точке х0, а
С – постоянная, то функция С· U
дифференцируема в этой точке и
3.(C U ) C U
7.
Правило 4• Если функции U и V
дифференцируемы в точке х0 и V не
равна 0, то их частное
дифференцируемо в этой точке и:
U U V U V
4.
2
V
V
8.
Правило 5n
(х )'
=
n1
n•х
9.
ПРИМЕР №110.
ПРИМЕР №211.
ВЫПОЛНИТЬ 5 ЗАДАНИЙ1. У = 20х4+10х
2. У = 60х+х5-15
3. У = Х27-20х +6
4. У = 25х2 +5х+15
5. У = 100 + 27х
6. У = 13х5 – 50х+3
7. У = х + 10х3 – 35х5
8. У = х-30 -7х+4
9. У = 36 + х25+х
6
12.
Вычислить производную:1. У = 5
2. У = х
3. У = Х25
4. У = Х30
5. У = х4
6. У = 6х
7. У = х5 – 50
8. У = 50х + х3 – 35
9. У = х-27
10. У = 36 + х25
11. У = х6 – 26х - 30
13.
Вычислить производную:12. У = 20х4+10х
13. У = 60х+х5-15
14. У = Х27-20х +6
15. У = 25х2 +5х+15
16. У = 100 + 27х
17. У = 13х5 – 50х+3
18. У = х + 10х3 – 35х5
19. У = х-30 -7х+4
20. У = 36 + х25+х
21. У = 2 х6 – 26х -33
14.
• 22. у = (3х + 2) (х + 1)23. у = (2х – 2)(х + 2)
24. у = х2(3х + х2)
• 25. у = 25х + 10
26. у = х13 + 30х + 120
27. у = 25х + 10х-12- 35х2
28. у = (2х + 2) (х + 1)
29. у = (х – 2)(х + 3)
30. у = х2(3х + х3)
31.у = √х
32. у = √х(2х2 –х)







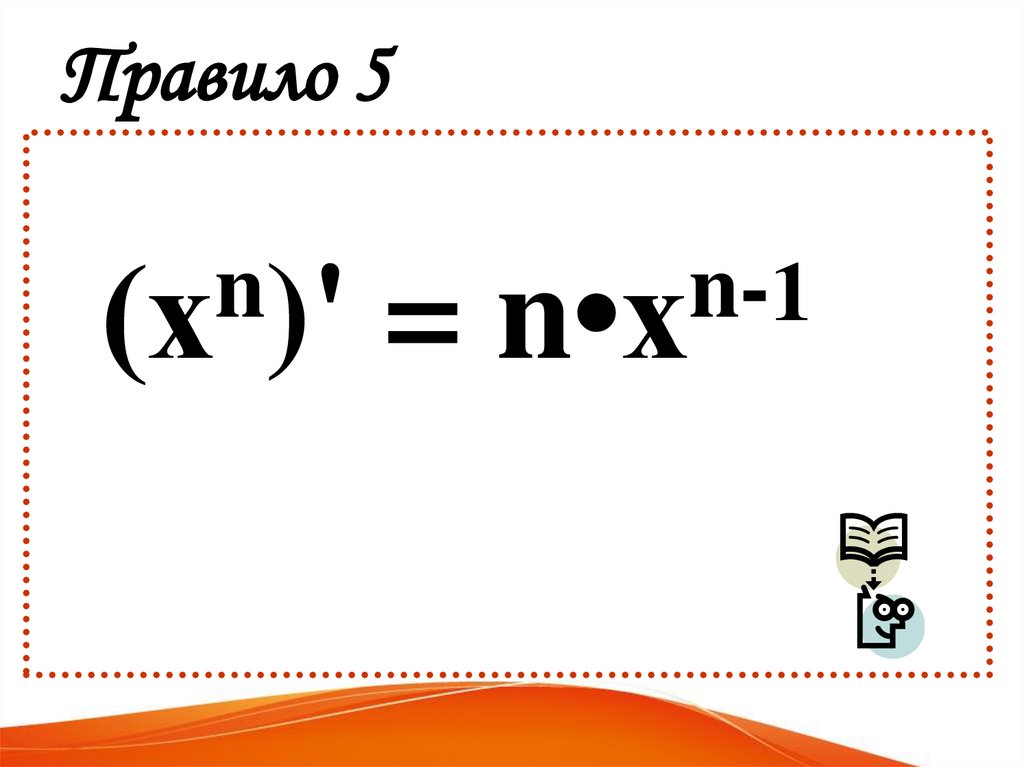





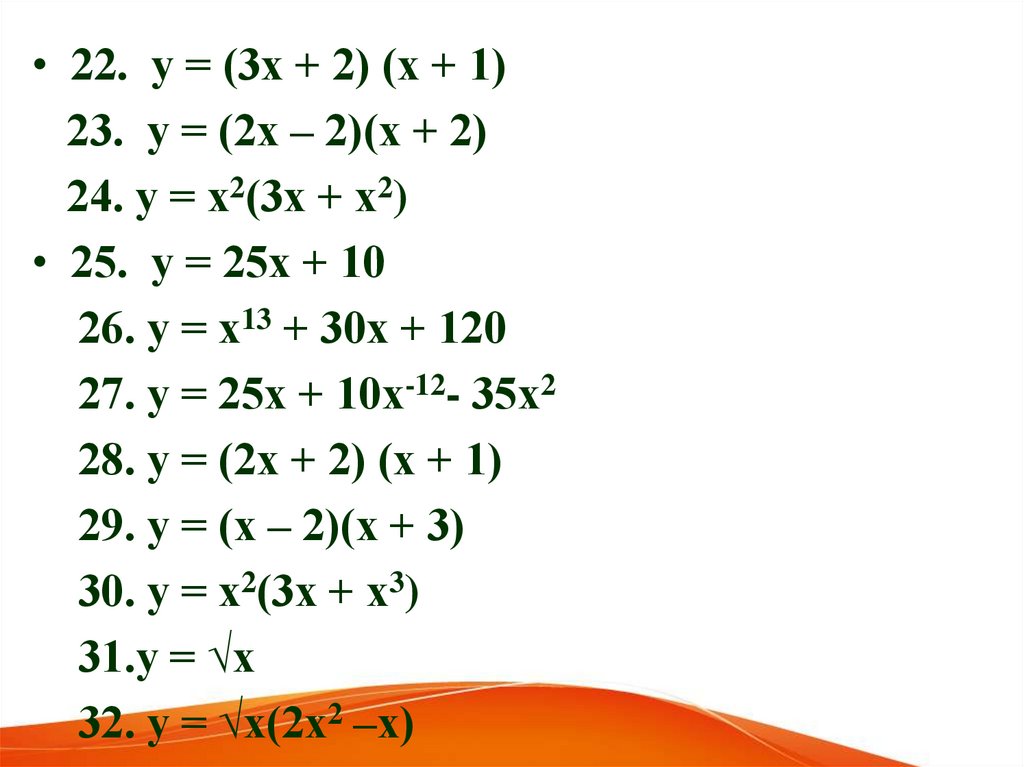
 Математика
Математика








