Похожие презентации:
Семинар 15. Изгибные колебания стержня (самостоятельная)
1.
Семинар 15. Изгибные колебания стержня (самостоятельная)Определить собственные частоты и формы изгибных колебаний стержня
EJ
L
1. Записать уравнение в частных производных.
д 4 w F д 2 w
0 (10.2)
4
2
дx
EJ дt
2. Записать решение, разделяя переменные по времени и координате
w ( x, t ) W ( x) sin t
( 10.3)
3. Подстановкой привести к обыкновенному дифференциальному уравнению
относительно форм колебаний
W IV 4W 0 (10.4)
4. Записать решение для форм колебаний
W ( x ) C1 sin x C2 cos x C3 sh x C4 ch x
( 10.5)
2.
EJL
5. Записать граничные условия относительно форм колебаний
д2w
д2w
w(0) 0, EJ 2 (0) 0, w( L) 0, EJ 2 ( L) 0
дx
дx
6. Составить условие ненулевого решения для определения собственных частот
W ( x ) C1 sin x C2 cos x C3 sh x C4 ch x
W ( x ) C1 2 sin x C2 2 cos x C3 2 sh x C4 2 ch x
3.
6. Составить условие ненулевого решения для определения собственных частотW ( x) C1 sin x C2 cos x C3 sh x C4 ch x
W ( x ) C1 2 sin x C2 2 cos x C3 2 sh x C4 2 ch x
W (0) 0 C2 *1 0 C4 *1 0
W (0) 0 C2 *1 0 C4 *1 0
C2 C4 0
C2 C4 0
C2 0 C4 0
W ( x) C1 sin x C3 sh x
W ( x ) C1 2 sin x C3 2 sh x
7. Записать выражение для определения собственных частот
W ( L) C1 sin L C3 sh L 0
W ( L) C1 sin L C3 sh L 0
4.
7. Записать выражение для определения собственных частотC1 sin L C3 sh L 0
C1 sin L C3 sh L 0
Преобразования
C1 sin L C3 sh L 0
C1 sin L C3 sh L 0
C1 sin L C3 sh L 0
C3 0
C1 sin L C3 sh L 0
sin L 0
L n
F
4
n 1,2,.....
EJ
2
n 2 2
n 2
L
8. Записать выражение для собственных форм колебаний
W ( x) C1 sin x
EJ
F
5.
Основные типы краевых условий для изгибных колебаний стержней1. w 0,
дw
0
дx
д2w
2. w 0, EJ 2 0
дx
д
д2 w
д2w
3. EJ 2 0, EJ 2 0
дx
дx
дx
д
д2w
д2 w
4. EJ 2 c1w 0, EJ 2 0
дx
дx
дx
д2w
дw
5. w 0, EJ 2 c2
0
дx
дx
6.
7.
8.
Основные типы краевых условий для продольныхколебаний стержней
1.
u = 0 при х=0
дu
2. EF 0 при x 0
дx
дu
4.2. EF cu 0 при x L
дx
2
дu
д
u
5.2. EF M 2
дt
дx
при x L
9.
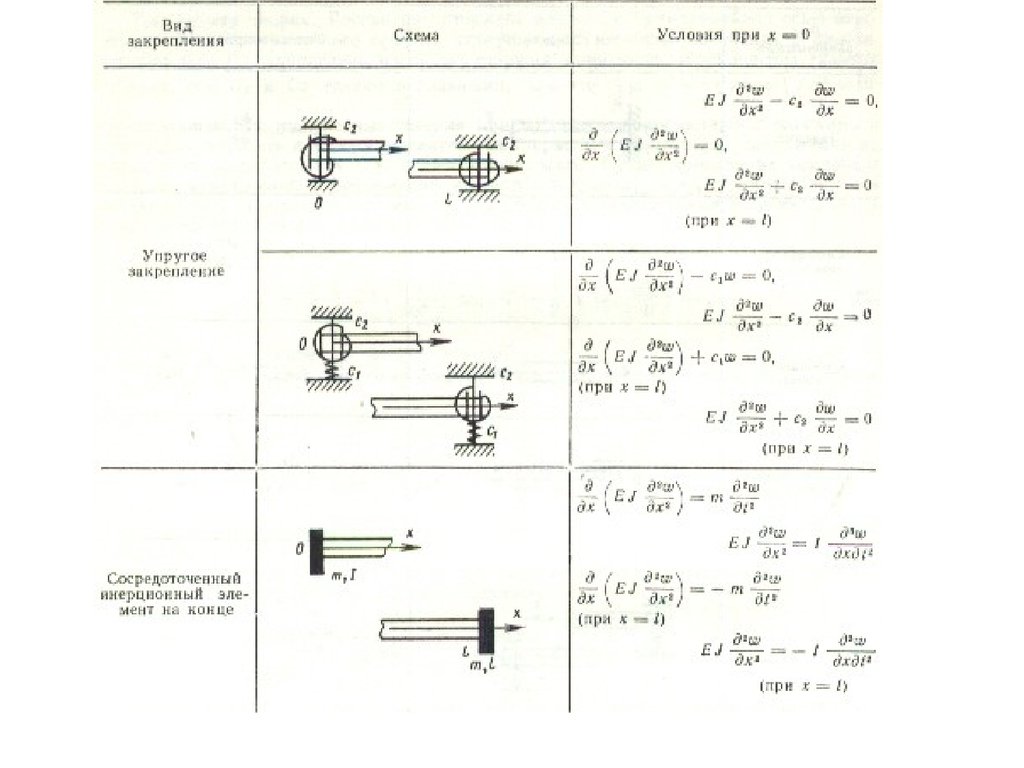
Основные типы краевых условий для крутильныхколебаний стержней
1. 0 при x 0
д
2. GJ к 0 при x 0
дx
д
4.2. GJ к c 0 при x L
дx
2
д
д
5.2. GJ к I x 2
дt
дx
при x L








 Механика
Механика








