Семинар 12. Изгибные колебания стержня

1.

Семинар 12. Изгибные колебания стержня

2.

Cобственные частоты и формы изгибных колебаний стержня
EJ
c
L
03
1 ch cos 3 ( sh cos ch sin ) 0 (10.19)
Если k k 1, 2, 3...
- корень уравнения (10.19), то собственная частота
k2
k 2
L
EJ
F
(10.20)
x
S1 ( k )
x
Wk ( x) S3 ( k )
S4 ( k )
L
S2 ( k )
L
(10.21)

3.

03
1 ch cos 3 ( sh cos ch sin ) 0 (10.19)
Некоторые другие граничные условия
2. При 0 0
(с=0) уравнение (10.19) переходит в уравнение (10.20),
совпадающее с уравнением для консольного стержня
ch cos 1 (10.20)
Корни уравнения
k
(2k 1)
2
1
3
1.57, 2
4.70
2
2

4.

Определить собственные частоты колебаний системы в Гц:
L = 60 м, сечение трубчатое d = 1 м и D=1.1 м , Е =2*1011 Н/м2, p=7800 кг/м3
1.57
1 2
L
EJ
F
J 2 ( D 2 d 2 )( D 2 d 2 ) ( D 2 d 2 )
2
2
F
4 ( D d )
2
3
1.57 E ( D 2 d 2 ) 1.57
1
.
57
5
.
4
10
1 2
2.9 10 6
2.36
L
2
3600
3600
1/с
1
f1
0.375 Гц
2
Формы собственных колебаний системы:
W ( x) ( sh x sin x)(ch x cos x) (ch x cos x)( sh x sin x) (10.23)

5.

03
1 ch cos 3 ( sh cos ch sin ) 0 (10.19)
3. При 0 (c )
уравнение (10.19) переходит в уравнение (10.21),
совпадающее с уравнением частот для стержня, один конец которого – заделка, а
второй свободно оперт
3
(1 ch cos ) ( sh cos ch sin ) 0 (10.19a )
3
0
tg tg 0 (10.21)
Корни уравнения
k
(2k 1)
4
1
3
5
2.36, 2
3.93
4
4

6.

Определить собственные частоты колебаний системы в Гц:
L = 60 м, сечение трубчатое d = 1 м и D=1.1 м , Е =2*1011 Н/м2, p=7800 кг/м3
2.36 EJ
1 2
L
F
J 2 ( D 2 d 2 )( D 2 d 2 ) ( D 2 d 2 )
2
2
F
4 ( D d )
2
3
2.36 E ( D 2 d 2 ) 2.36
2
.
36
5
.
4
10
1 2
2.9 106
3.54
L
2
3600
3600
f1
1/с
1
0.554 Гц
2
Формы собственных колебаний системы:
W ( x) ( sh x sin x)(ch x cos x) (ch x cos x)( sh x sin x) (10.24)

7.

8.

Изгибные колебания неразрезных балок
Более предпочтительно в этом случае использовать уравнения трех моментов
(m - номер пролета, совпадающий с номером правой опоры):
M m 1
S 4, m
1
2
2
( EJ ) m S 2, m S 4, m
S 2, m S 3, m S1, m S 4, m
1
2
2
( EJ ) m
S 2, m S 4, m
Mm
S 2, m 1 S 3, m 1 S1, m 1 S 4, m 1
1
2
2
S 2, m 1 S 4, m 1
( EJ ) m 1
M m 1
S 4, m 1
1
( EJ ) m 1 S 22, m 1 S 42, m 1
(10.24)
Если все пролеты одинаковы, то (10.24) принимает вид
M m 1S 4, m 2 M m S 2, m S 3, m S1, m S 4, m M m 1S 4, m 1
(10.25)

9.

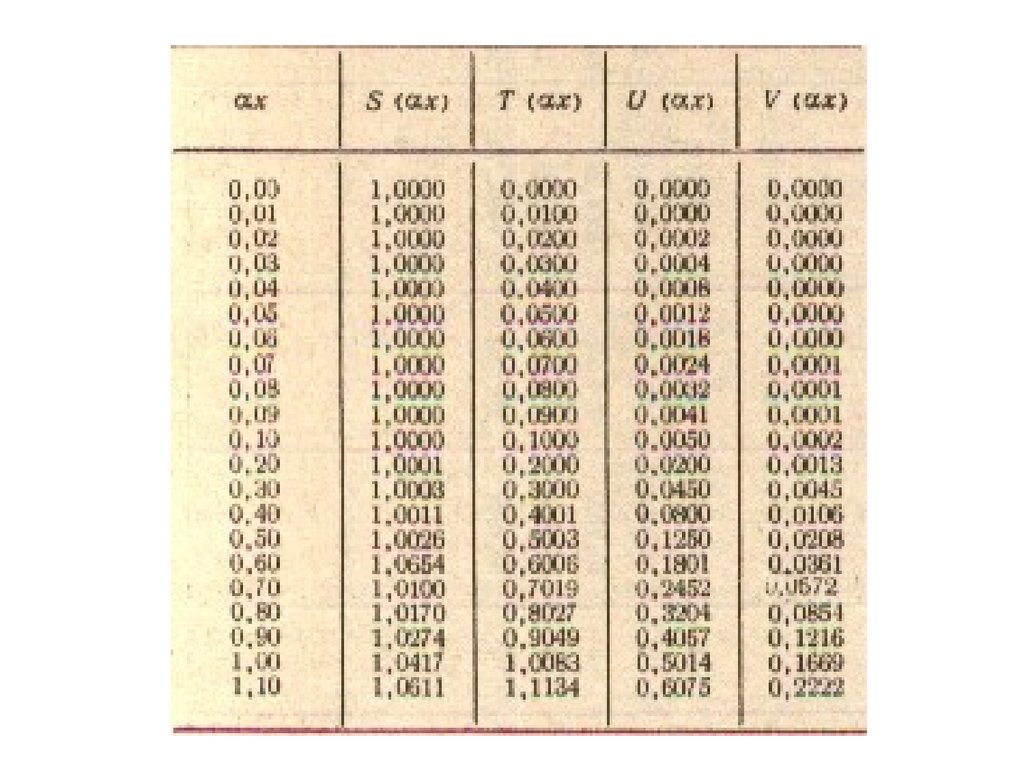
Данные для многопролетных неразрезных стержней приведены в табл. 7
Частоты неразрезных стержней с равными пролетами образуют «зоны сгущения». В каждой такой зоне
находится число частот, равное числу пролетов стержней, а значения частот близки между собой.