Похожие презентации:
Выпуклый анализ. Субградиент и субдифференциал функциил. Лекция 19
1. ВЫПУКЛЫЙ АНАЛИЗ
ЛЕКЦИЯ 197. СУБГРАДИЕНТ И СУБДИФФЕРЕНЦИАЛ ФУНКЦИИ
(ПРОДОЛЖЕНИЕ)
2.
7. СУБГРАДИЕНТ И СУБДИФФЕРЕНЦИАЛФУНКЦИИ (ПРОДОЛЖЕНИЕ)
7.5. Критерий минимума для субдифференцируемых функций.
3.
7.5. Критерий минимума для субдифференцируемых функций.множеств U R n и функций
Теорема 5.
Пусть
I : U R1 ,
Для произвольных
справедливо следующее утверждение.
I : U R1 , U R n . Для того, чтобы точка u U была
точкой минимума функции
выполнение включения
I
на множестве
0 ¶I ( u ) .
Доказательство. Пусть
U
необходимо и достаточно
u - точка минимума функции I
на множестве
U.
I ( u ) = min I (u ) Þ I (u ) ³ I ( u ) "u U Þ
u U
I (u ) ³ I ( u ) + 0, u - u , "u U Þ 0 ¶I ( u ) .
Обратно
0 ¶I ( u ) Þ I (u ) ³ I ( u ) + 0, u - u , "u U Þ
I (u ) Þ
I (u ) ³ I ( u ) "u U Þ I ( u ) = min
u U
Теорема доказана.
Для выпуклых функций, определенных на выпуклых множествах, справедлив более
содержательный результат.
4.
Теорема 6. Пусть Wвыпуклая функция и
I
1
R n - открытое выпуклое множество, I : W R
U W
- выпуклое подмножество. Для того, чтобы функция
достигала своей нижней грани на множестве
достаточно, чтобы существовал субградиент
U
в точке
u U
c = c( u ) ¶I ( u )
необходимо и
такой, что
c , u - u ³ 0, "u U .
Необходимость. Пусть
{
}
u U = u U I ( u ) = inf I ( u ) = I > -¥ .
В пространстве
u U
R n +1 введем множества
ìï
üï
æuö
n +1
A = ía = ç ÷ R u W , a0 ³ I ( u ) - I ý ,
è a0 ø
ïî
ïþ
ìï æ v ö
üï
ìï æ v ö
üï
n +1
n +1
B = íb = ç ÷ R v U , b0 < 0 ý Þ B = íb = ç ÷ R v U , b0 £ 0 ý .
ïî è b0 ø
ïþ
ïî è b0 ø
ïþ
5.
ìïüï
æuö
n +1
A = ía = ç ÷ R u W , a0 ³ I ( u ) - I ý ,
è a0 ø
ïî
ïþ
ìï æ v ö
üï
n +1
B = íb = ç ÷ R v U , b0 < 0 ý ,
u
ïî è b0 ø
ïþ
I
A
I = I ( u)
u I
U W
B
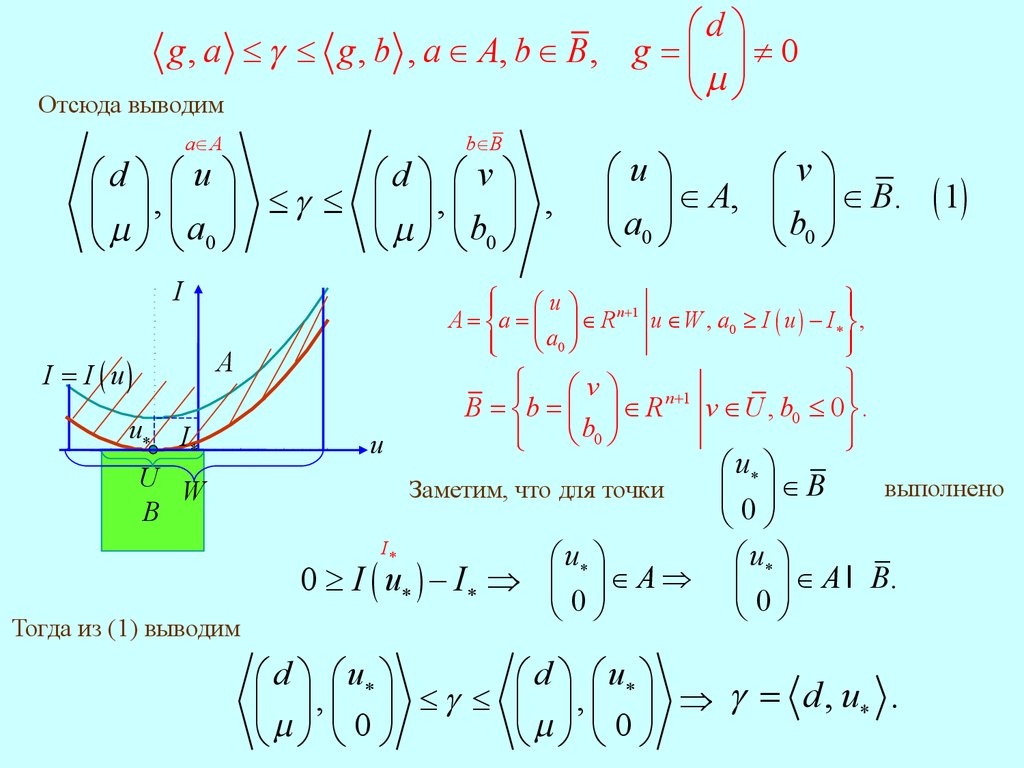
Введенные множества
Факт выпуклости множества
A
A
Действительно, пусть
B
являются выпуклыми.
доказывается аналогично выпуклости надграфика
выпуклой функции теорема 4.1. Выпуклость множества
A I B = Æ.
и
æuö
ç ÷ A.
è a0 ø
B
очевидна. Покажем, что
min I ( u )
u U
Тогда, либо
u U Þ I ( u ) - I ³ 0 Þ
a0 ³ 0, либо u W \ U . В обоих случаях a Ï B и A I B = Æ.
æd ö
Тогда существует гиперплоскость с нормальным вектором g = ç ÷ ¹ 0, отделяющая
èmø
множества
AÉ A
и
B,
т.е
g , a £ g £ g , b , a A, b B.
6.
æd ög , a £ g £ g , b , a A, b B , g = ç ÷ ¹ 0
mø
è
Отсюда выводим
a A
b B
æd ö æ u ö
æd ö æ v ö
ç ÷, ç a ÷ £ g £ ç ÷, çb ÷ ,
èmø è 0 ø
èmø è 0 ø
I
u
I
U W
B
Тогда из (1) выводим
( 1)
ìï
üï
æuö
A = ía = ç ÷ R n +1 u W , a0 ³ I ( u ) - I ý ,
è a0 ø
ïî
ïþ
A
I = I ( u)
æuö
ævö
ç ÷ A, ç ÷ B.
è a0 ø
è b0 ø
u
ìï æ v ö
üï
n +1
B = íb = ç ÷ R v U , b0 £ 0 ý .
îï è b0 ø
þï
æ u ö
выполнено
Заметим, что для точки
ç ÷ B
è0ø
I
æ u ö
æ u ö
0 ³ I ( u ) - I Þ ç ÷ A Þ ç ÷ A I B.
è0ø
è0ø
æ d ö æ u ö
æ d ö æ u ö
ç ÷ , ç ÷ £ g £ ç ÷ , ç ÷ Þ g = d , u .
èmø è 0 ø
èmø è 0 ø
7.
d , uæd ö æ u ö
æd ö æ v ö
ç ÷, ç a ÷ £ g £ ç ÷, çb ÷
èmø è 0 ø
èmø è 0 ø
Неравенство (1)
( 1)
æd ö æ u ö
æd ö æ v ö
ç ÷ , ç a ÷ £ d , u £ ç ÷ , ç b ÷ ,
èmø è 0 ø
èmø è 0 ø
перепишем в виде
Þ
æuö
ævö
d , u + m a0 £ d , u £ d , v + m b0 , ç ÷ A, ç ÷ B
è a0 ø
è b0 ø
Из правого неравенства в (2) при
получим
u
( 2)
ìï æ v ö
æ u ö
n +1 v U ,
b = ç ÷ B = íb = ç ÷ R
b0 £ 0
è -1 ø
îï è b0 ø
üï
ý
þï
-1
d , u £ d , v + m b0 = d , u - m Þ d , u £ d , u - m Þ m £ 0.
Покажем, что m
< 0. Пусть все же m = 0.
Тогда из левого неравенства в (2) выводим
d , u £ d , u , "u W .
(3)
8.
Полагаем в (3)e >0
d , u £ d , u , "u W
настолько мало,
что
u = u + e d W .
d , u + e d £ d , u Þ
Получили противоречие с тем, что
Разделим (2)
(3) u = u + e d ,
где
Из (3) выводим
>0
e d 2 £ 0 Þ d = 0.
æd ö
g = ç ÷ ¹ 0.
èmø
m < 0.
Таким образом ,
d , u + m a0 £ d , u £ d , v + m b0
( 2)
на
В результате получим
d
d
d
, u + a0 ³
, u ³
, v + b0 .
m
m
m
d
Полагаем c = - , Тогда
m
- c , u + a0 ³ - c , u ³ - c , v + b0 ,
"u W , a0 ³ I ( u ) - I , "v U , b0 £ 0 Þ
m < 0.
9.
- c , u + a0 ³ - c , u ³ - c , v + b0 , - c , u - u + a0 ³ 0 ³ - c , v - u + b0 ,"u W , a0 ³ I ( u ) - I , "v U , b0 £ 0 .
При
a0 = I ( u ) - I
I ( u ) - I
}
из левого неравенства в (4) - c , u - u + a0 ³ 0
( 4)
- c , u - u + I ( u ) - I ³ 0 Þ
находим
I ( u )
I ( u ) - I ³ c , u - u , "u W Þ c ¶I ( u )
При
b0 = 0
из правого неравенства в (4) находим
0
c , v - u ³ b0 = 0 Þ c , v - u ³ 0, "v U U .
Необходимость
$c ¶I ( u ) : c , u - u ³ 0, "u U доказана.
u U
c , u - u ³ 0, "u U .
u
c
Достаточность. Пусть для некоторой точки
По определению субградиента
и
c ¶I ( u )
выполнено
( 5)
I (u ) ³ I ( v ) + c , u - v , c ¶I (v)
( 5)
тогда
6 44 7 4 48
I ( u ) - I ( u ) ³ c , u - u ³ 0, "u U Þ u U .
Достаточность доказана. Теорема доказана полностью.
( 4)
10.
Замечание. Как видно из доказательства теоремы множестваA, B R n +1
d
æd ö
n +1
g = ç ÷ R , субградиент c = - ¶I ( u ) не зависят от выбора
m
èmø
Упражнение.
ìïæ u1 ö üï
I ( u ) = max íç 2 ÷ ý ,
ïîè u ø ïþ
Для
u2
1
1
u
u1
Здесь
-1
ìïæ u1 ö 1
üï
2
U = íç 2 ÷ u £ 1, u £ 1ý .
ïîè u ø
ïþ
æ -1ö
u = ç ÷ .
è -1ø
Решение.
Тогда
ìï æ c1 ö
üï
¶I ( u ) = íc = ç ÷ c1 + c2 = 1, c1 ³ 0, c2 ³ 0 ý .
ïî è c2 ø
ïþ
æ 12 ö
В качестве c ¶I ( u ) возьмем вектор c = ç ÷ .
1
è2ø
Тогда
u U .
проверить выполнение теоремы 6 $c ¶I ( u ) : c , u - u ³ 0
U
-1
и
вектор
и
z ( u ) = { 1, 2}
u2
1 ¶I ( u )
Uu
-u
c
-1
u
1
-1
u1
11.
æ 12 ö æ u1 - ( -1) ö1 1 2
c , u - u = ç 1 ÷ , çç 2
÷÷ = ( u + u ) + 1 ³ 0
2
è 2 ø è u - ( -1) ø
для всех
ìïæ u1 ö 1
üï
æ u1 ö
2
ç 2 ÷ U = íç 2 ÷ u £ 1, u £ 1ý .
èu ø
ïîè u ø
ïþ
Теорема 6. Пусть
выпуклая функция и
I
1
W R n - открытое выпуклое множество, I : W R
U W
- выпуклое подмножество. Для того, чтобы функция
достигала своей нижней грани на множестве
достаточно, чтобы существовал субградиент
U
в точке
c = c ( u ) ¶I ( u )
c , u - u ³ 0, "u U .
Следствие. Пусть в условиях доказанной теоремы
обеспечивающий неравенство (5),
u U
необходимо и
такой, что
( 5)
u int U .
Тогда субградиент,
может быть только нулевым вектором.
12.
<0Действительно,
u int U Þ u = u + e c U ,
достаточно мало. Из (5)
( 5)
c , u - u ³ 0, "u U
<0
при
e £ e0,
для такого
где
e0 > 0
u U
выводим
<0
c , u + e c - u ³ 0 Þ e c 2 ³ 0 Þ c = 0.
Таким образом, проверка точек
включения
0 ¶I ( u ) .
Пример 4.
u = 0 int U .
Пусть
Действительно,
{
( 5)
<
>
с × u < 0.
}
с = 0 ¶I ( 0 ) = c R1 c £ 1 .
{
}
с ¶I (0) = c R1 c £ 1 ,
c , u - u ³ 0, "u U
>
<
на оптимальность сводится к проверке
æ 12 ö
Почему в упражнении c = ç 1 ÷ ¹ 0?
è2ø
I ( u ) = u , u U = R1. Здесь U = { u } = { 0}
Очевидно, что
других субградиентов
u int U
0
и
Покажем, что
обеспечивающих неравенство (5),
c , u - uс ³u 0, Þ u× R
³ 0, "
1
,
не существует.













 Математика
Математика Программирование
Программирование








