Похожие презентации:
Формулы сокращённого умножения. Урок 86
1.
2.
№ 28.7(б) Преобразуйте квадрат двучлена в многочлен стандартного вида:(– 6у – 2z)2 = (6у + 2z)2 =
(I + II)2 = I2 + II2 + 2·I·II
= (6у)2 + (2z)2 + 2 · 6у · 2z =
= 36у2 + 4z2 + 24уz
или = 36у2 + 24уz + 4z2
3.
№ 28.8(б) Преобразуйте квадрат двучлена в многочлен стандартного вида:2
2
1
1
1
2
4 m +3n = 4 m +(3n) +2 4 m 3n =
(I + II)2 = I2 + II2 + 2·I·II
1
3
2
2
=
m +9n + mn
16
2
4.
№ 28.9(б) Преобразуйте квадрат двучлена в многочлен стандартного вида:(у2 – 6)2 = (у2)2 + 62 – 2 · у2 · 6 = у4 + 36 – 12у2
(I – II)2 = I2 + II2 – 2·I·II
№ 28.10(б)
(b2 – 5у)2 = (b2)2 + (5у)2 – 2 · b2 · 5у =
= b4 + 25у2 – 10b2у
или = b4 – 10b2у + 25у2
5.
№ 28.11(б) Преобразуйте квадрат двучлена в многочлен стандартного вида:(m2 – n3)2 = (m2)2 + (n3)2 – 2 · m2 · n3 =
(I – II)2 = I2 + II2 – 2·I·II
= m4 + n6 – 2m2n3
6.
№ 28.12(б) Преобразуйте квадрат двучлена в многочлен стандартного вида:(4х2 – 3с)2 = (4х2)2 + (3с)2 – 2 · 4х2 · 3с =
(I – II)2 = I2 + II2 – 2·I·II
= 16х4 + 9с2 – 24сх2
7.
№ 28.33(а,б) Преобразуйте выражение в многочленстандартного вида:
а) 3(х – у)2 = 3( х2 + у2 – 2ху ) =
(I – II)2 = I2 + II2 – 2·I·II
= 3х2 + 3у2 – 6ху
8.
№ 28.33(а,б) Преобразуйте выражение в многочленстандартного вида:
б) – с(3а + с)2 = – с((3а)2 + с2 + 2 · 3а · с ) =
(I + II)2 = I2 + II2 + 2·I·II
= – с(9а2 + с2 + 6ас) = – 9а2с – с3 – 6ас2
9.
№ 28.34(а,б) Преобразуйте выражение в многочленстандартного вида:
а) а2 + (3а – b)2 = а2 + 9а2 + b2 – 6аb =
(I – II)2 = I2 + II2 – 2·I·II
= 10а2 + b2 – 6аb
10.
№ 28.34(а,б) Преобразуйте выражение в многочленстандартного вида:
б) 9р2 – (q – 3р)2 = 9р2 – (q2 + 9р2 – 6pq) =
(I – II)2 = I2 + II2 – 2·I·II
= 9р2 – q2 – 9р2 + 6pq = – q2 + 6pq = 6pq – q2
11.
№ 28.35(а,б) Преобразуйте выражение в многочленстандартного вида:
а) (а – 4)2 + а(а + 8) =
(I – II)2 = I2 + II2 – 2·I·II
= а2 + 16 – 8а + а2 + 8а = 2а2 + 16
12.
№ 28.35(а,б) Преобразуйте выражение в многочленстандартного вида:
б) (х – 7)х + (х + 3)2 =
(I + II)2 = I2 + II2 + 2·I·II
= х2 – 7х + х2 + 9 + 6х = 2х2 – х + 9
13.
№ 28.58(а,б) Замените символы * одночленами так,чтобы выполнялось равенство:
(6а5 + *)2 = * + 25х2 + *
(6а5 + 5х)2 = 36а10 + 25х2 + 60а5х
(10m5 + *)2 = * + 36m4n6 + *
(10m5 + 6m2n3)2 = 100m10 + 36m4n6 + 120m7n3
14.
05.09.2020К л а с с н а я р а б о т а.
Формулы сокращённого
умножения (ФСУ).
15.
(p + n)(p – n)p2 – pn + pn – n2 =
p2 – n2
p2 – n2
(k + m)(k – m)
k2 – km + km – m2 =
k2 – m2
k2 – m2
16.
a2 – b2разность квадратов
равна разности квадратов этих
выражений
Выучить!
17.
(I + II)(I – II) = I2 – II2х 2 – 22 = х 2 – 4
(9у)2 – 12 = 81у2 – 1
82 – (7k)2 = 64 – 49k2
(3n)2 – (5c)2 = 9n2 – 25c2
18.
55
8c
3x
–
m
m
2b
4y
8c
3x
–
а2
49
4b2
–
–
16y2
19.
49 · 51 = (50 – 1)(50 + 1) = 502 – 12 == 2500 – 1 = 2499
1 6
10 9
7 7
2
1
1
1
2
10+ 7 10 7 = 10 =
7
1
48
= 100
= 99
49
49
20.
РТ № 28.24а) 48 · 52 = (50 – 2)(50 + 2) = 502 – 22 =
= 2500 – 4 =2496
б) 39 · 41 = (40 – 1)(40 + 1) = 402 – 12 =
= 1600 – 1 = 1599
в) 57 · 63 = (60 – 3)(60 + 3) = 602 – 32 =
= 3600 – 9 = 3591
г) 22 · 18 = (20 + 2)(20 – 2) = 202 – 22 =
= 400 – 4 = 396
21.
РТ № 28.25а) 0,48 · 0,52 = 0,2496
б) 0,39 · 0,41 = 0,1599
в) 0,57 · 0,63 = 0,3591
г) 0,22 · 0,18 = 0,0396
22.
РТ № 28.262 1
а) 4 5
3 3
2
1
1
1
2
5 3 5+ 3 = 5 =
3
8
1
= 25 = 24
9
9
2
2
2
2 7
2
2
б) 10 9 10+ 10 = 10 =
7
7 7
7
7
45
4
= 100
= 99
49
49
23.
РТ № 28.262
1
в) 99 100
3
3
1
1
100 3 100+ =
3
2
8
1
1
= 100 = 10000 = 9999
9
9
3
2
4 1
4
г) 7 8,2 7 8
5 5
5
2
1
1
8 5 8+ =
5
24
1
1
= 63
= 8 = 64
25
25
5
2
24.
№ 28.23(в,г) Выполните действия, используя соответствующую формулу сокращённогоумножения:
в) (4b + 1)(1 – 4b) = (1 + 4b)(1 – 4b) =
(I + II)(I – II) = I2 – II2
= 12 – (4b)2 = 1 – 16b2
г) (5m + 2)(2 – 5m) = (2 + 5m)(2 – 5m) =
= 22 – (5m)2 = 4 – 25m2
25.
№ 28.24(в,г) Выполните действия, используя соответствующую формулу сокращённогоумножения:
в) (13c – 11d)(13c + 11d) = (13c)2 – (11d)2 =
(I – II)(I + II) = I2 – II2
= 169c2 – 121d2
г) (8m – 9n)(8m + 9n) = (8m)2 – (9n)2 =
= 64m2 – 81n2
26.
№ 28.26(в,г) Выполните действия, используя соответствующую формулу сокращённогоумножения:
в) (3n4 – m4)(3n4 + m4) = (3n4)2 – (m4)2 =
(I – II)(I + II) = I2 – II2
= 9n8 – m8
г) (10m8 + 8n8)(10m8 – 8n8) =
= (10m8)2 – (8n8)2 = 100m16 – 64n16
27.
У: стр. 113 § 28З: § 28 № 20 – 28(а,б).





















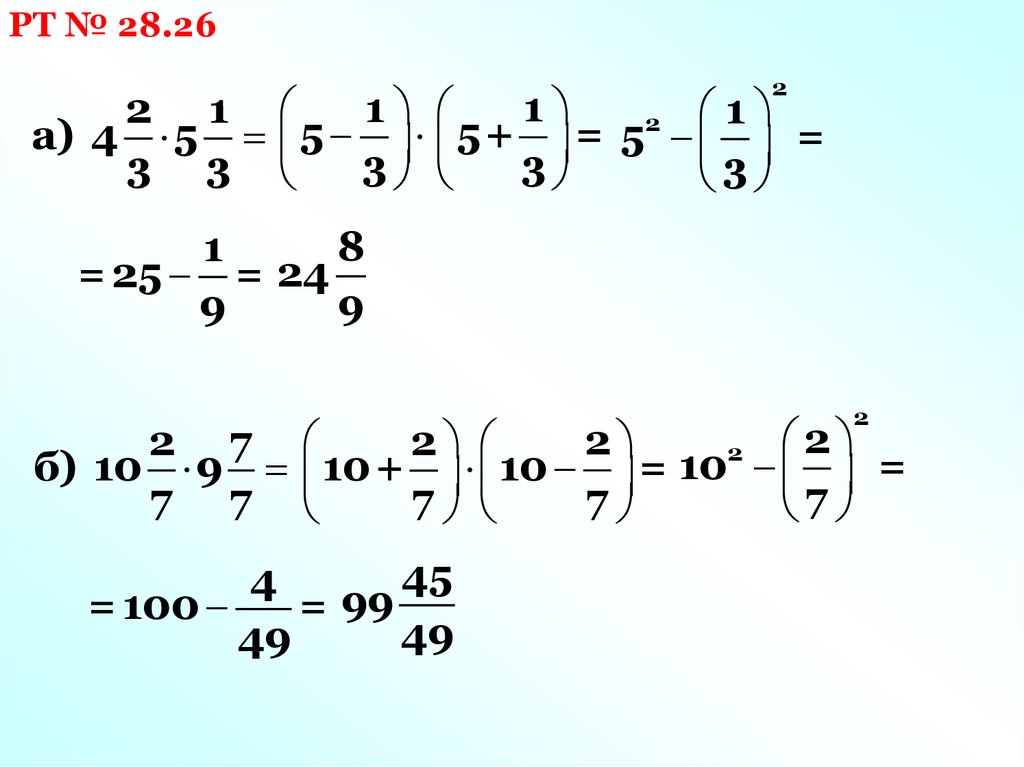





 Математика
Математика








