Похожие презентации:
Структура курса. Теория. Пакет Statistica
1.
СТРУКТУРА КУРСАТеория
пакет Statistica
Приложения
Корреляционный анализ
Статистика автокомбината
Регрессионный анализ
Простая
Множественная
Нелинейная
Центробанк
АСМАП
Маршрутная сеть
Дисперсионный анализ
Террамеханика
Многомерный анализ
Факторный
Кластерный
Дискриминантный
Планирование эксперимента
Оптимизация планов
Последовательное планирование
Стохастическая аппроксимация
Характеристика автомобилей
Поставки запчастей
2.
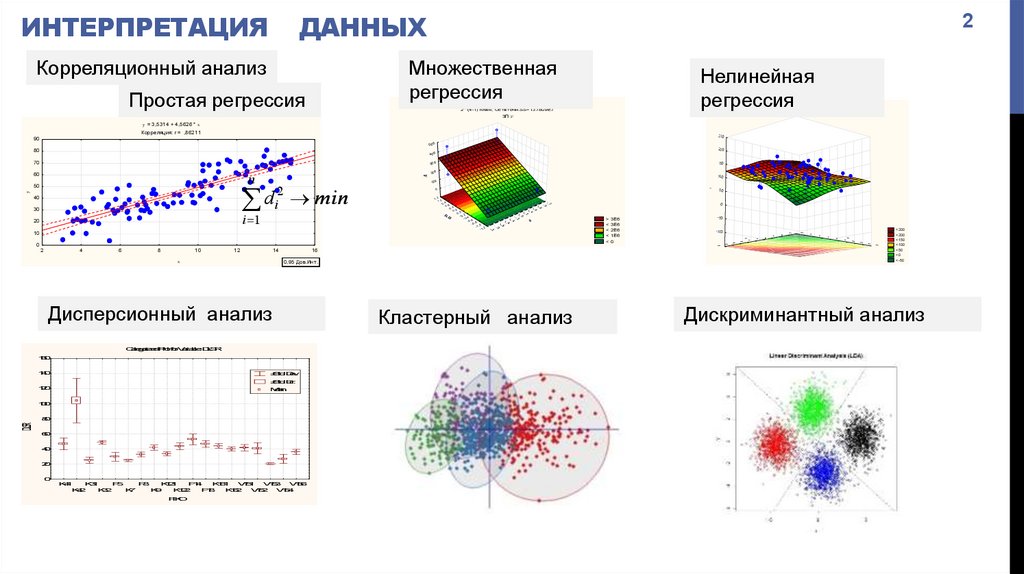
ИНТЕРПРЕТАЦИЯДАННЫХ
Корреляционный анализ
2
Множественная
регрессия
Простая регрессия
Нелинейная
регрессия
Подогнанная поверхнос ть; Перемен.: F
2**(4-1) план; Ос таточн.SS=137809E7
ЗП F
y = 3,5314 + 4,5626 * x
Корреляция: r = ,86211
250
90
5E6
200
80
4E6
70
150
3E6
F
y
30
i 1
20
0
1,2
1,0
0,8
0,6
0,4
mu
0,2
0,0
2
- 0, ,4
-0 ,6
-0
- 0,
10
-
-0, 0,4
8
6
-1, 0,8
0
- 1 , , 2 -1
0
,2
-1
0
0,2 ,4
0
-0, ,0
2
1
1,0 ,2
0
0,6 ,8
s
0
2
4
6
8
10
12
14
16
0,95 Дов.Инт.
x
Дисперсионный анализ
C
a
te
g
o
r
iz
e
dP
lo
tfo
rV
a
r
ia
b
le
:D
L
S
R
1
6
0
1
4
0
±
S
td
.D
e
v
.
±
S
td
.E
r
r
.
1
2
0
M
e
a
n
1
0
0
DLSR
8
0
6
0
4
0
2
0
0
K
4
1
K
3
1
F
5
F
8
K
1
2
1
F
1
4
K
1
6
1
V
1
5
1
V
1
5
3
V
1
5
6
K
4
2
K
3
2
K
7
K
9
K
1
2
2
F
1
8
K
1
6
2
V
1
5
2
V
1
5
4
F
IK
O
Кластерный анализ
50
0
>
<
<
<
<
3E6
3E6
2E6
1E6
0
-50
-100
4
40
100
1E 6
y
d i2 min
50
2E 6
0
n
-
60
> 200
< 200
< 150
< 100
< 50
<0
< -50
Дискриминантный анализ
3.
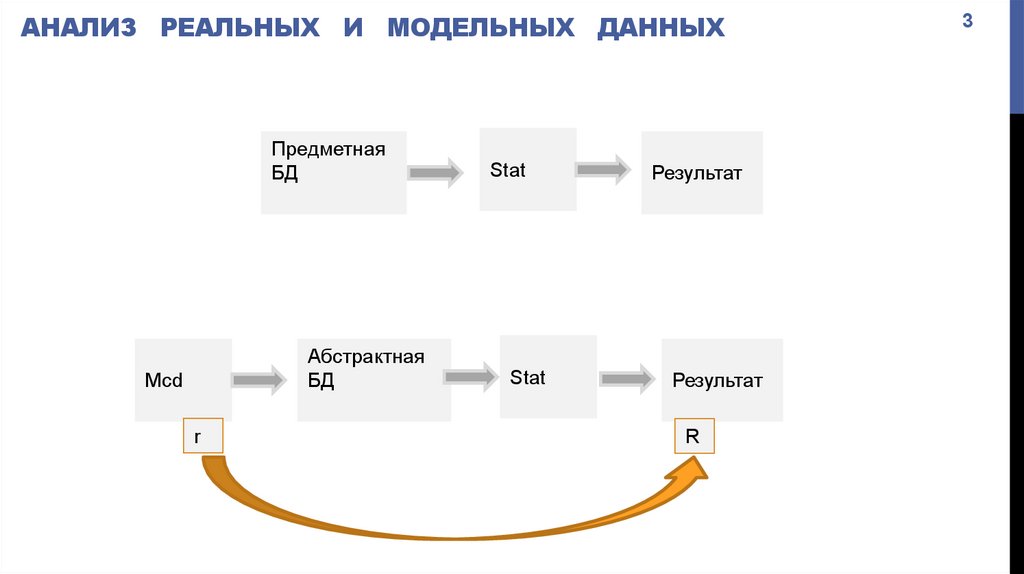
АНАЛИЗ РЕАЛЬНЫХ И МОДЕЛЬНЫХ ДАННЫХПредметная
БД
Абстрактная
БД
Mcd
r
Stat
Stat
Результат
Результат
R
3
4.
МАТРИЧНЫЕ ОПЕРАЦИИ В MATHCADmatrix(L,N,f) - создание матрицы - L – число строк, N – число столбцов, f - функция f(l,n)
identity(n) - создание единичной матрицы размерности n
diag(v) - создание диагональной матрицы с элементами главной диагонали из v;
geninv(А) - обращение матрицы А, аналогично операции А-1.
rows(А) - определение числа строк матрицы А
cols(А) - определение числа столбцов матрицы А
last(v) - вычисление номера последнего элемента вектора v
lenght(v) - вычисление количества элементов v
csort(А,i), rsort(А,j) - сортировка по возрастанию элементов i–го столбца или строки
min(А), max(А) - минимальный и максимальный элемент матрицы
tr(A) - след квадратной матрицы A
rank(A) - ранг матрицы A
norm1(A), norm2(A), norme(A), normi(A) - нормы квадратной матрицы A
submatrix (M, r1, r2, c1, c2) - подматрица М, r1 и r2 – нижний и верхний номер строки, с1 и с2 - нижней и верхний
номер столбца матрицы М
augment(A,B,…), stack(A,B,…) - слияние матриц А, В, … слева направо или сверху вниз
rref(A) - приведение матрицы к ступенчатому виду с единичным базисным минором
eigenvals(A) - собственные значения квадратной матрицы А
eigenvecs(A) - собственные вектора квадратной матрицы А по порядку собственных значений
eigenvec(A, l) - собственный вектор для собственного значения
lsolve(A, b) - решение СЛАУ Ax=b
4
5.
MATLAB5
6.
STATISTICA6
7.
СООТВЕТСТВИЕ ТЕРМИНОЛОГИИОбозначение
A, B
A+B = A B
AB
A
A/B
AB=
A=B
A B
Теория множеств
Множеств, пространство
Элемент множества
Подмножество A, B
Объединение множеств
Пересечение множеств
Дополнение множества
Разность множеств
Пустое множество
Множества не пересекаются
Множества равны
A есть подмножество B
7
Теория вероятностей
Пространство элементарных событий
Элементарное событие
Случайное событие A, B
Сумма событий
Произведение событий
Противоположное событие
Разность событий
Невозможное событие
События несовместны
События равносильны
Событие A влечет событие B
8.
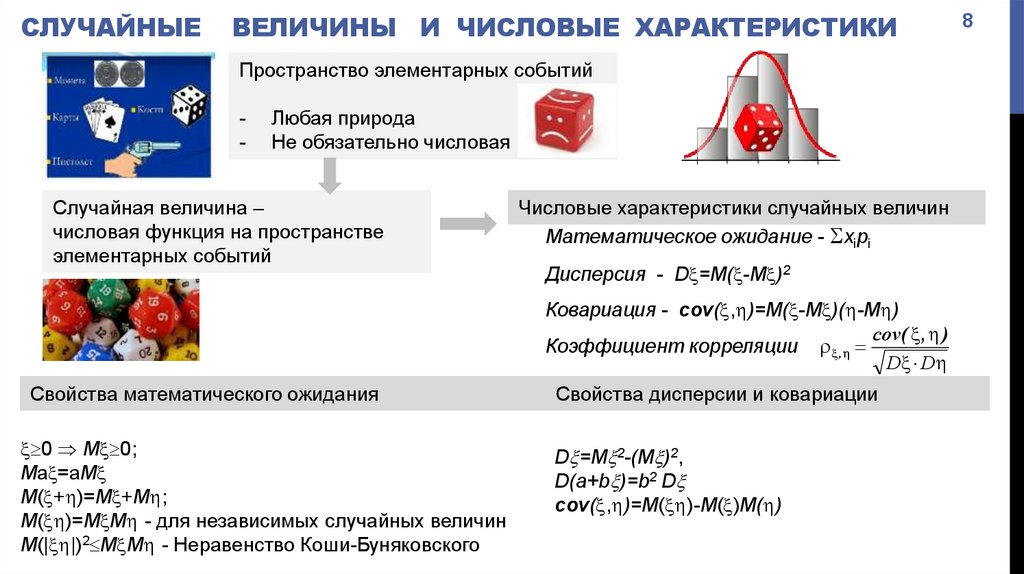
СЛУЧАЙНЫЕВЕЛИЧИНЫ И ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
Пространство элементарных событий
-
Любая природа
Не обязательно числовая
Случайная величина –
числовая функция на пространстве
элементарных событий
Числовые характеристики случайных величин
Математическое ожидание - xipi
Дисперсия - D =M( -M )2
Ковариация - cov( , )=M( -M )( -M )
cov( , )
Коэффициент корреляции ,
D D
Свойства математического ожидания
0 M 0;
Ma =aM
M( + )=M +M ;
M( )=M M - для независимых случайных величин
M(| |)2 M M - Неравенство Коши-Буняковского
Свойства дисперсии и ковариации
D =M 2-(M )2,
D(a+b )=b2 D
cov( , )=M( )-M( )M( )
8
9.
ИГРА В КОСТИ+
ПЕТЕРБУРГСКИЙ ПАРАДОКС
9
10.
СЛУЧАЙНЫЕВЕКТОРЫ
Случайный вектор
1 1 2
2
...
11 12
21 22
n
Математическое
ожидание
n
M 1
M
2
M
...
M n
10
Дисперсионная матрица - D =||cov( i, j)||ij=1..n
Свойства D : D – симметрична (D=DT)
D - неотрицательно-определенная ( X: XTDX 0)
D - дисперсионная матрица D=ATA
Представление D: D = M[( -M )( -M )T]
Некоторые доказательства
cov i , j xi x j M i M i j M j xi x j M i M i xi
2
i, j
i, j
0
i, j
D=ATA DT = (ATA)T = AT(AT)T = ATA = D
D=ATA X: XTDX = XT(ATA)X = (XTAT)(AX) = (AX)T(AX) = YTY = yi2 0
11.
ПРЕДСТАВЛЕНИЕ ДИСПЕРСИОННОЙ МАТРИЦЫM M M
T
1 M 1
...
i M i 1 M 1
...
n M n
1 M 1 2
...
M i M i 1 M 1
...
M M
n
1
1
n
2
M 1 M 1
...
M i M i 1 M 1
...
M M M
n
n
1
1
... j M j
... n M n
...
1 M 1 j M j
...
1 M 1 n M n
...
...
...
...
...
...
...
...
...
...
...
...
i M i j M j
n M n j M j
... i M i n M n
...
...
2
n M n
...
M 1 M 1 j M j ... M 1 M 1 n M n
...
...
...
M i M i j M j ... M i M i n M n || cov i , j || D
...
...
2
M n M n j M j ...
M n M n
11
12.
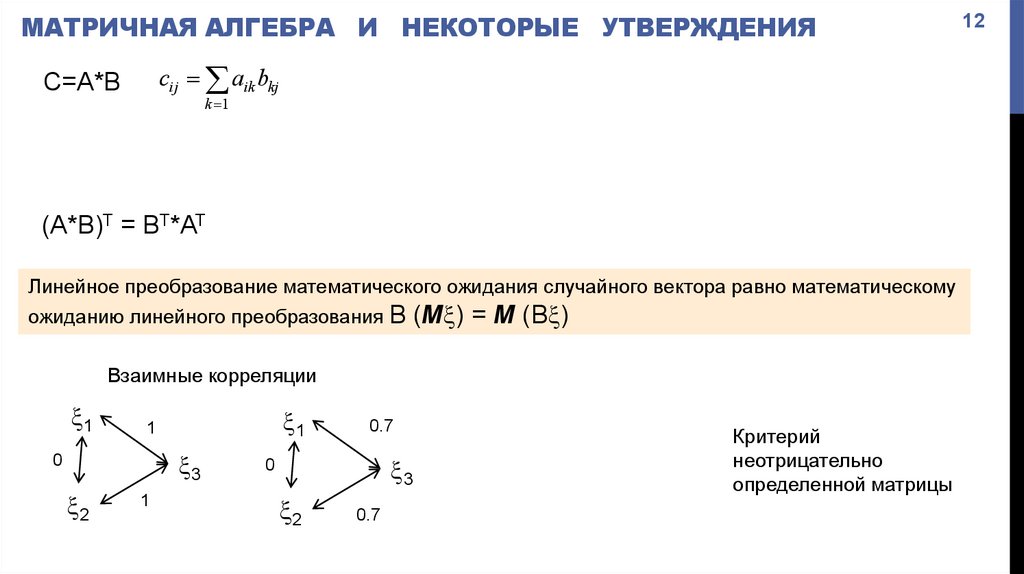
МАТРИЧНАЯ АЛГЕБРА И НЕКОТОРЫЕ УТВЕРЖДЕНИЯсij aik bkj
C=A*B
k 1
(A*B)T = BT*AT
Линейное преобразование математического ожидания случайного вектора равно математическому
ожиданию линейного преобразования В (M ) = M (В )
Взаимные корреляции
1
1
1
3
0
2
1
0.7
3
0
2
0.7
Критерий
неотрицательно
определенной матрицы
12
13.
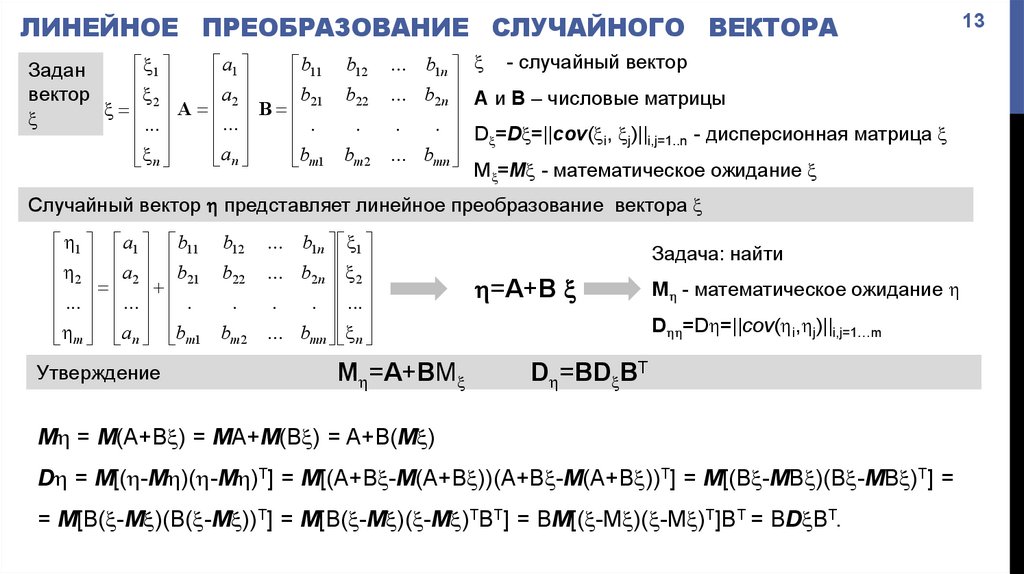
ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ СЛУЧАЙНОГО ВЕКТОРАa1
b11 b12
1
Задан
a
b
b22
вектор
2
2
21
A
B
...
.
.
...
a n
n
bm1 bm 2
... b1n - случайный вектор
... b2 n A и B – числовые матрицы
.
. D =D =||cov( , )||
i
j i,j=1..n - дисперсионная матрица
... bmn
M =M - математическое ожидание
Случайный вектор представляет линейное преобразование вектора
1 a1 b11 b12
a b
b22
2 2 21
.
... ... .
m a n bm1 bm 2
Утверждение
... b1n 1
... b2 n 2
.
. ...
... bmn n
M =A+BM
Задача: найти
=A+B
M - математическое ожидание
D =D =||cov( i, j)||i,j=1…m
D =BD BT
M = M(A+В ) = MA+M(В ) = A+В(M )
D = M[( -M )( -M )T] = M[(A+В -M(A+В ))(A+В -M(A+В ))T] = M[(В -MВ )(В -MВ )T] =
= M[В( -M )(В( -M ))T] = M[В( -M )( -M )TВT] = ВM[( -M )( -M )T]ВT = ВD ВT.
13
14.
ТЕОРЕМА О НОРМАЛЬНОЙ КОРРЕЛЯЦИИ14
Оптимальное оценивание нормально-распределенных случайных векторов
1 ,..., m
T
Совместный случайный вектор
M
m
m
D
D
D
1 ,..., m
T
Минимизация суммы квадратов
1 ,..., m , 1 ,..., m T
- математическое ожидание совместного вектора
D
D
D cov i , j
D cov i , j
D cov i , j
- дисперсионная матрица совместного вектора
Утверждение
1 i, j m
1 i m, 1 j n
1 i, j n
Оценка вектора
1
m
M | m D D
Ошибка оценка вектора
1
D D D
D
15.
ТЕОРЕМА О НОРМАЛЬНОЙ КОРРЕЛЯЦИИ (ДОКАЗАТЕЛЬСТВО)1
m
, m D D
1
m 0
M M m M D D
D M m m 0
T
Доказать
Вывод: и некоррелированы в силу нормальности распределения - независимы
Оптимальная оценка по это M =0 - 1-ое утверждение доказано
1
2
|
1
D M T D D D
D
Доказать
15
16.
ВЫВОД ФОРМУЛ ТЕОРЕМЫ О НОРМАЛЬНОЙ КОРРЕЛЯЦИИ1
m m
D M m m M m M m D D
T
T
16
1
m m M m m D D 1 M m m
M m m D D
T
T
1
D D D
D 0
1
m m D D 1 m
D M T m D D
T
m m T m D D 1 m T
M
D D 1 m m T D D 1 m D D 1 m T
1
M m m M m m D
D
T
T
1
m m MD D 1 m m D 1D
MD D
T
1
1
1
1 T
D D D
D D D
D D D
D D
D
1
D D D
D
T
17.
СЛУЧАЙ НЕЗАВИСИМЫХ ПРЕДИКТОРОВ И СКАЛЯРНОЙПРОГНОЗИРУЕМОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
1 ,..., n , T
(n+1)-мерный гауссовский вектор, причем 1, 2 … n попарно независимы
cov( i, j)=0, а является одномерной величиной,
17
18.
НАЗВАНИЕ СЛАЙДА18
19.
НАЗВАНИЕ СЛАЙДА19
20.
MATHCAD- определение размеров матрицы
Xn- ввод нижнего индекса
x-1 - вычисление обратной матрицы
|x| - определитель матрицы |M|=detM или длина вектора |x|
- поэлементные операции с матрицами
M<> - M<j> j-й столбец матрицы
MT - транспонирование матрицы
û ê - скалярное произведение векторов x*y= xiyi
û ê - векторное произведение a b=(a2b3-a3b2, a3b1-a1b3, a1b2-a2b1);
x - сумма компонент вектора x= xi
m..n - диапазон изменения переменной
20
21.
НАЗВАНИЕ СЛАЙДА21
D M m m M m
T
M m m D
M m D D 1 m m
T
m T m
T
M m m D D 1 M m m
1
D
D D D 1 D
D M T m D D 1 m m D D 1 m
T
m m T m D D 1 m T
M
D D 1 m m T D D 1 m D D 1 m T
M m m M m m D 1 D
T
T
MD D 1 m m MD D 1 m m D 1 D
T
T
D D D 1 D D D 1 D D D 1 D D 1 D
T
D D D 1 D
T
















 Математика
Математика