Определитель 3 порядка

1.

Определитель 3-го порядка
ПУСТЬ ДАНА СИСТЕМА ИЗ ТРЕХ ЛИНЕЙНЫХ
У РА В Н Е Н И Й ОТ Н О С И Т Е Л Ь Н О Т Р Е Х Н Е И З В Е СТ Н Ы Х

2.

Определителем третьего порядка,
назовем число D, равное
a
a
11 12
D a
a
21 22
a
a
31 32
a
13
a
23
a
33
a11a22a33 a12a23a31 a13a32a21 a13a22a31 a11a23a32 a33a21a12

3.

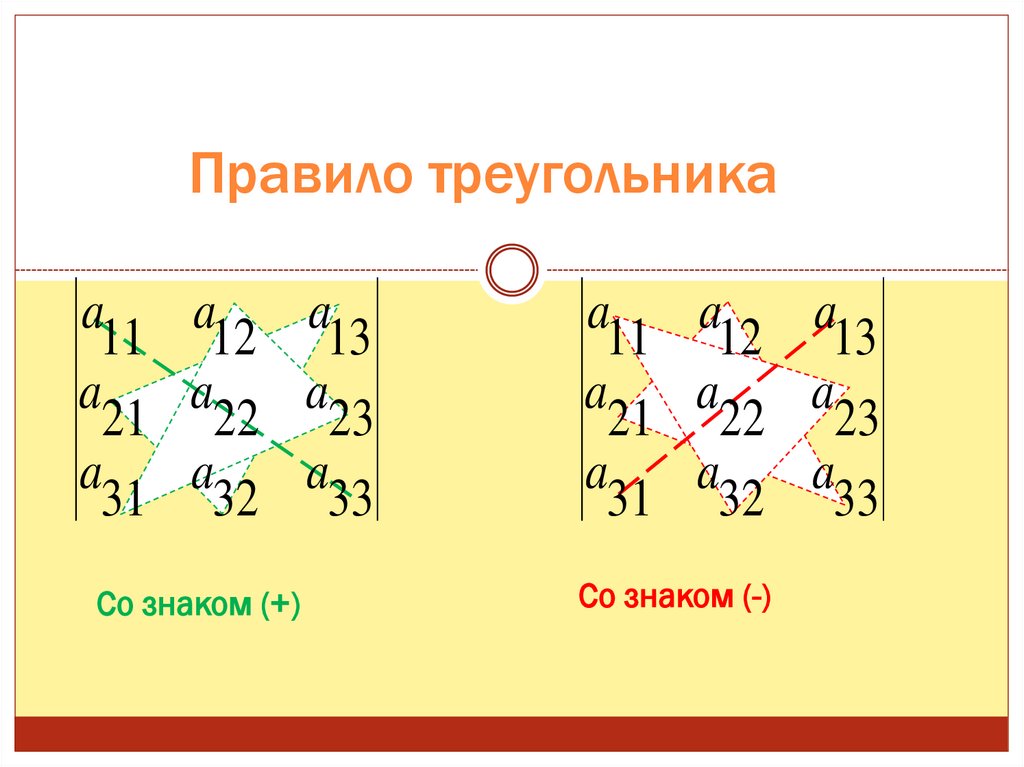
Правило треугольника
a
a
a
11 12 13
a
a
a
21 22 23
a
a
a
31 32 33
Со знаком (+)
a
a
a
11 12 13
a
a
a
21 22 23
a
a
a
31 32 33
Со знаком (-)

4.

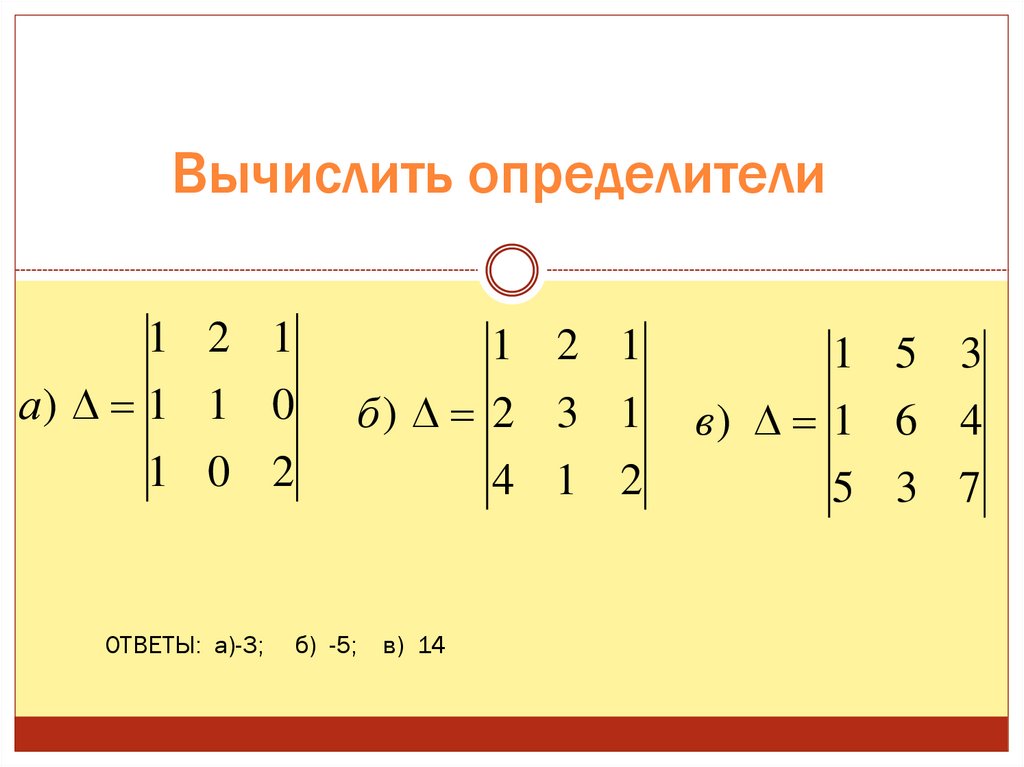
Вычислить определители
1 2 1
1 2 1
а) 1 1 0
1 5 3
б) 2 3 1
в) 1 6 4
1 0 2
4 1 2
5 3 7
ОТВЕТЫ: а)-3;
б) -5; в) 14

5.

Решить уравнения
1).
3
5
7
x
4
6
1
x
3
0
2).
x
1 2
3
4 5
2 1 x
1 2 2
3). 1
3
1
3
x2
2
5 x
3
4
8
2 4
3 7
0
0

6.

Свойства определителя 3-го порядка
Свойство 1. Величина определителя не изменяется
при замене строк столбцами.
1 1 2
5 3 1 17
4 1 3
1 5 4
1 3 1
2 1 3
Свойство 2. При перестановке двух строк (столбцов) между собой, величина
определителя меняет знак.
1 1 1
3
2
2 11
5
4
1
3
2
2
1 1 1
5
4
1

7.

Свойство 3. Определитель с двумя одинаковыми
5
(пропорциональными) строками (столбцами)
5
равен нулю.
5 2
5 1
5 5 3
Свойство 4. Если все элементы некоторой строки
(столбца) содержат одинаковый множитель,
то этот множитель можно вынести за знак определителя.
2 4 6
1 2 3
1 1 2 6 2 1 1 2 2*3
3 1 1
3 1 1

8.

Свойство 6. Определитель, содержащий две
пропорциональные строки, равен нулю.
Свойство 7. Величина определителя не изменится, если
к элементам некоторой строки (столбца) добавить
соответствующие элементы другой строки(столбца),
предварительно умножив их на один и тот же
множитель.