Похожие презентации:
Уравнение прямой
1.
2.
Цель:Сформировать представление студентов о
линиях представленных рациональными
уравнениями первого порядка
Задачи:
Изучить различные способы задания
прямой на плоскости
Изучить общее уравнение прямой
Рассмотреть взаимное расположение
прямых
3.
Способы задания прямойОбщее уравнение прямой
Взаимное расположение прямых на
плоскости
Угол между прямыми
Расстояние от точки до прямой
4.
NM y bk tg
BN
x
y kx b
y
Если k 0, то BM Ox и
В
уравнение прямой y b
α
Если
M
α
b
0
Oy , уравнение x c
N
x
90 , то tg не существует
прямая BM
y-b
C
x
5.
Пусть М 1 AB, поэтомуy1 kx1 b.
y
y1
y y1 k(x x1 )
B
A
Выделив b и подставив в
уравнение y kx b, получим
M1
0
x1
x
6.
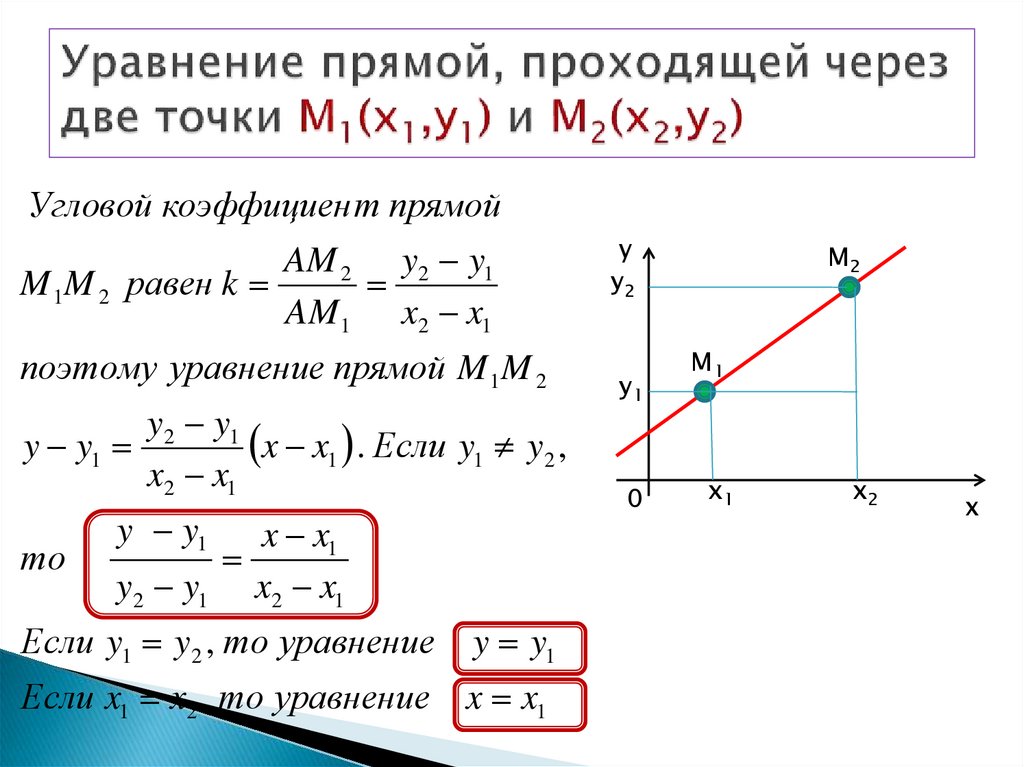
Угловой коэффициен т прямойAM 2 y2 y1
M 1M 2 равен k
AM 1 x2 x1
поэтому уравнение прямой M 1M 2
y2 y1
x x1 . Если y1 y2 ,
y y1
x2 x1
то
y y1
x x1
y2 y1 x2 x1
Если y1 y2 , то уравнение
y y1
Если x1 x2 , то уравнение x x1
y
у2
у1
0
М2
М1
x1
x2
x
7.
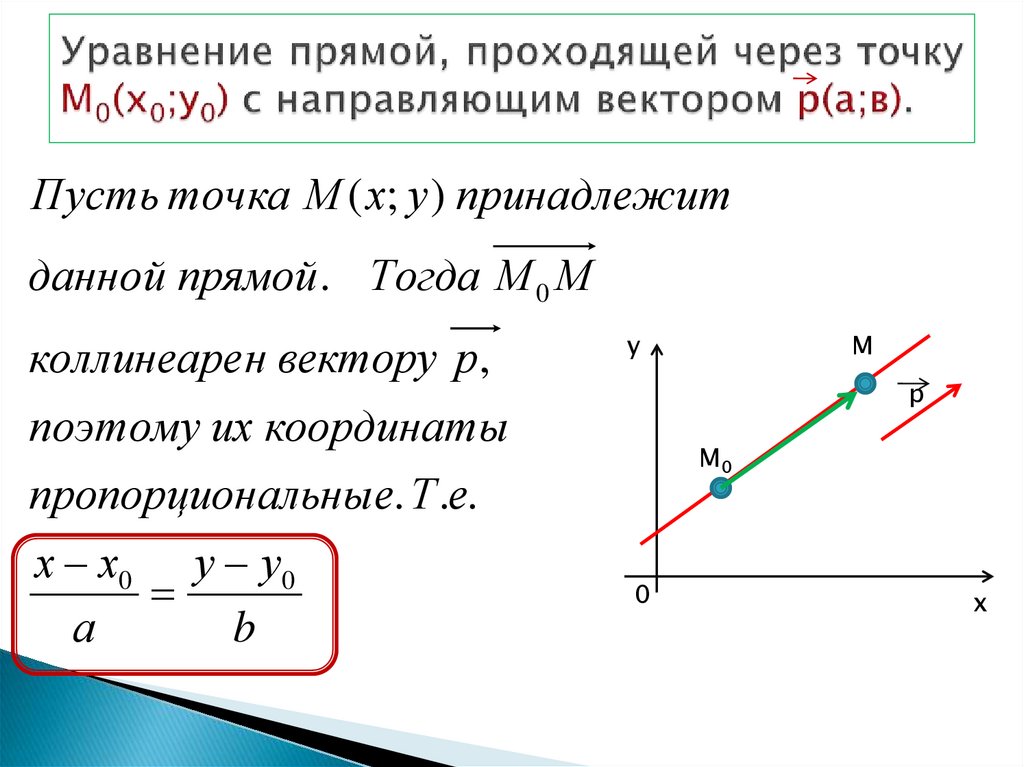
Пусть точка М ( х; у ) принадлежитданной прямой . Тогда М 0 М
коллинеаре н вектору р,
y
р
поэтому их координаты
М0
пропорциональные. Т .е.
х х0 у у0
а
b
М
0
x
8.
Теорема В прямоугольной системекоординат любая прямая задается
уравнением первой степени
Ax By C 0
.
И, обратно, уравнение Ax By C 0
при
произвольных коэффициентах А,В,С (А и В
одновременно не равны 0) определяет
некоторую прямую в прямоугольной
системе координат.
9.
Если С=0, то прямая с уравнением Ах+Ву=0проходит через начало координат.
Если В=0 (А≠0), то прямая с уравнением
Ах+С=0 проходит параллельно оси Оу
через точку (-С/А;0). Если В=С=0, то это
уравнение оси Оу х=0.
Если А=0 (В≠0), то прямая с уравнением
Ву+С=0 проходит параллельно оси Ох
через точку (0;-С/В). Если А=С=0, то это
уравнение оси Ох у=0.
10.
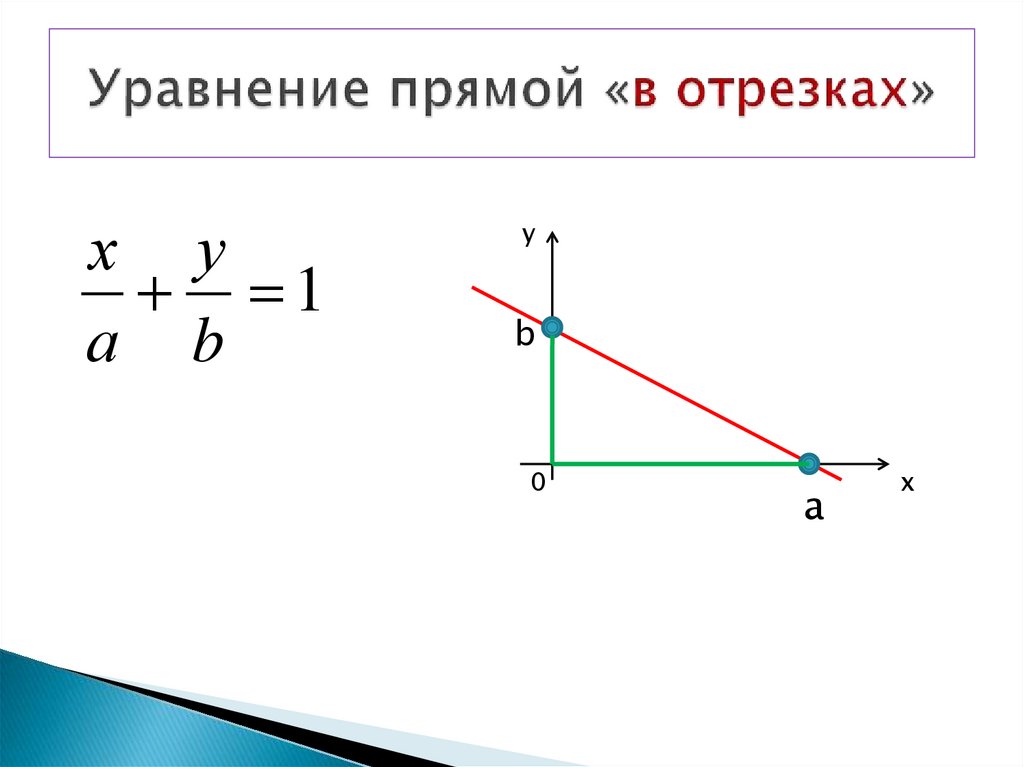
х у1
а b
y
b
0
a
x
11.
Любое линейное уравнение являетсяуравнением прямой.
Любая прямая задается уравнением первого
порядка.
По линейному уравнению можно
определить взаимное расположение
прямых.









 Математика
Математика








