Похожие презентации:
Определитель и его свойства
1. Определитель и его свойства
2.
Определитель квадратной матрицыесть некоторое
число, которое вычисляется из
элементов матрицы по определенному
правилу
3.
Вычисление определителей1. Определитель 1-го порядка равен самому элементу
1 a11 a11
1 2 2,
Например:
1 7 7
2. Определитель 2-го порядка находится по правилу
2
a
b
c
d
a d b c
Определитель 2-го порядка равен разности произведений
элементов главной и побочной диагонали.
2
2 3
4
Например:
2
5
2 5 ( 3) 4 10 ( 12) 10 12 22
6 2
3
7
( 6) 7 ( 2) ( 3) 42 6 48
4.
3 24 5
3 5 2 4 15 8 7
5. Определитель 3 порядка можно вычислить 3 способами:
• Разложением по элементам 1 строки• Метод треугольника или диагональный
метод
• Методом Саррюса
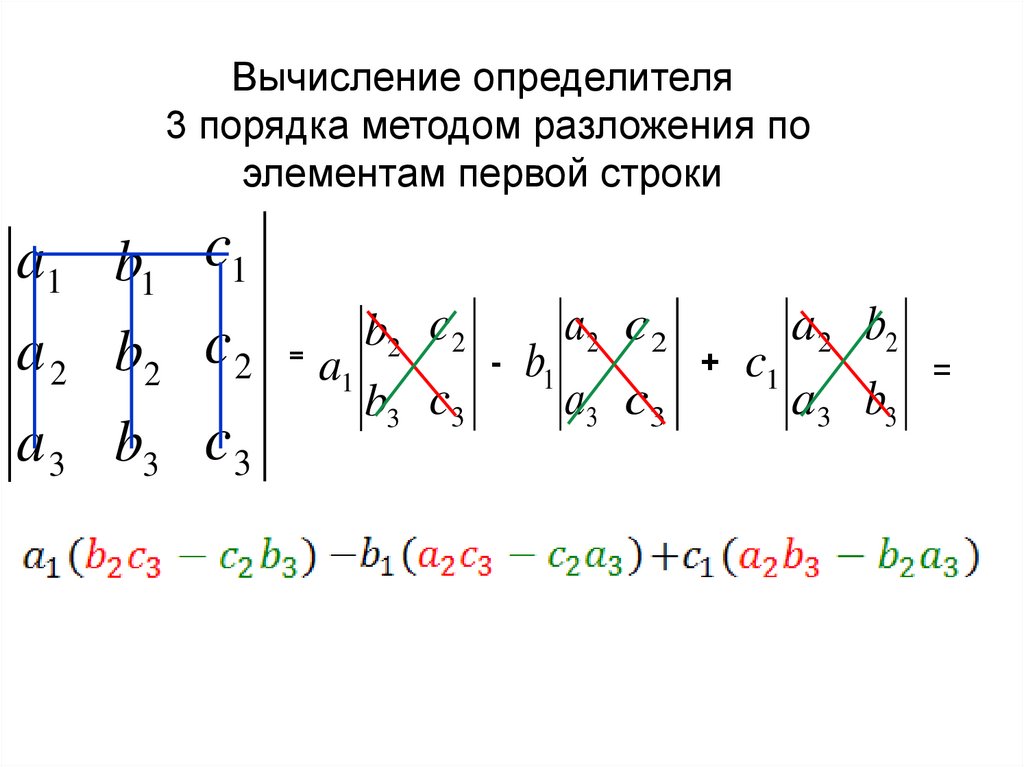
6.
Вычисление определителя3 порядка методом разложения по
элементам первой строки
a1 b1 c1
a 2 b2 c 2
a 3 b3 c3
=
a1
b2 c2
b3 c3
-
b1
a2 c2
a 3 c3
+
c1
a 2 b2
a3 b3
=
7.
1 2 34 5 6 1
7 8 9
5 6
8 9
2
4 6
7 9
3
4 5
7 8
1 5 9 8 6 2 4 9 7 6 3 4 8 7 5
3 12 9 0
8.
a1b1
c1
a2
b2
c2
a3
b3
c3
-
=
9.
1 2 34 5 6 1 5 9 2 6 7 4 8 3
7 8 9
7 5 3 8 6 1 4 2 9
45 84 96 105 48 72 0
10.
a1b1
c1
a1
a2
b2
c2
a 2 b2
a3
b3
c3
a3
b1
b3
=
11.
1 2 31 24 5 6 4 5 1 5 9 2 6 7 3 4 8
7 8 97 8
7 5 3 8 6 1 9 4 2
45 84 96 105 48 72 0
12. Основные свойства определителей.
• 1. Определитель не изменится, если егостроки заменить столбцами, и наоборот.
• 2. При перестановке двух параллельных
рядов определитель меняет знак.
• 3. Определитель, имеющий два
одинаковых ряда равен нулю.
• 4. Если все элементы одного ряда
умножить на некоторое число k, то весь
умножится на это число.
13. Основные свойства определителей.
• 5. Если все элементы некоторого рядапропорциональны соответствующим
элементам параллельного ряда, то такой
равен 0.
• 6. Если элементы какого-либо ряда
представляют собой
• суммы двух слагаемых, то может быть
разложен на сумму двух соответствующих
определителей.
14. Основные свойства определителей.
• 7. Определитель не изменится, если кэлементам одного ряда прибавить
соответствующие элементы параллельного
ряда, умноженные на любое число.



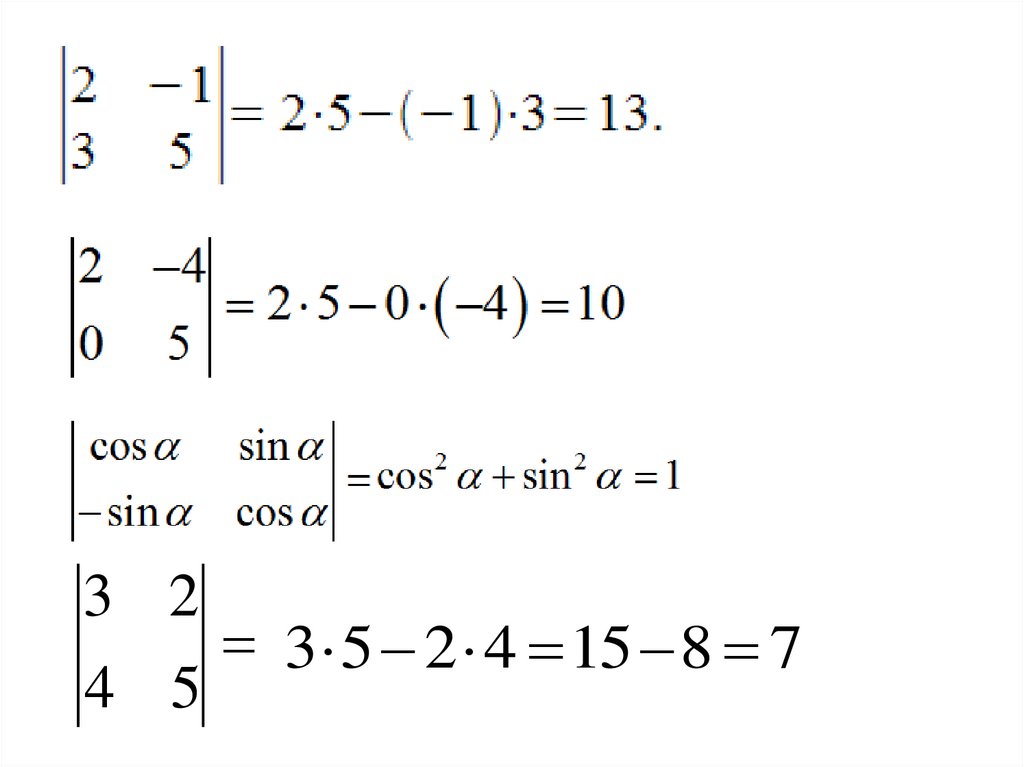

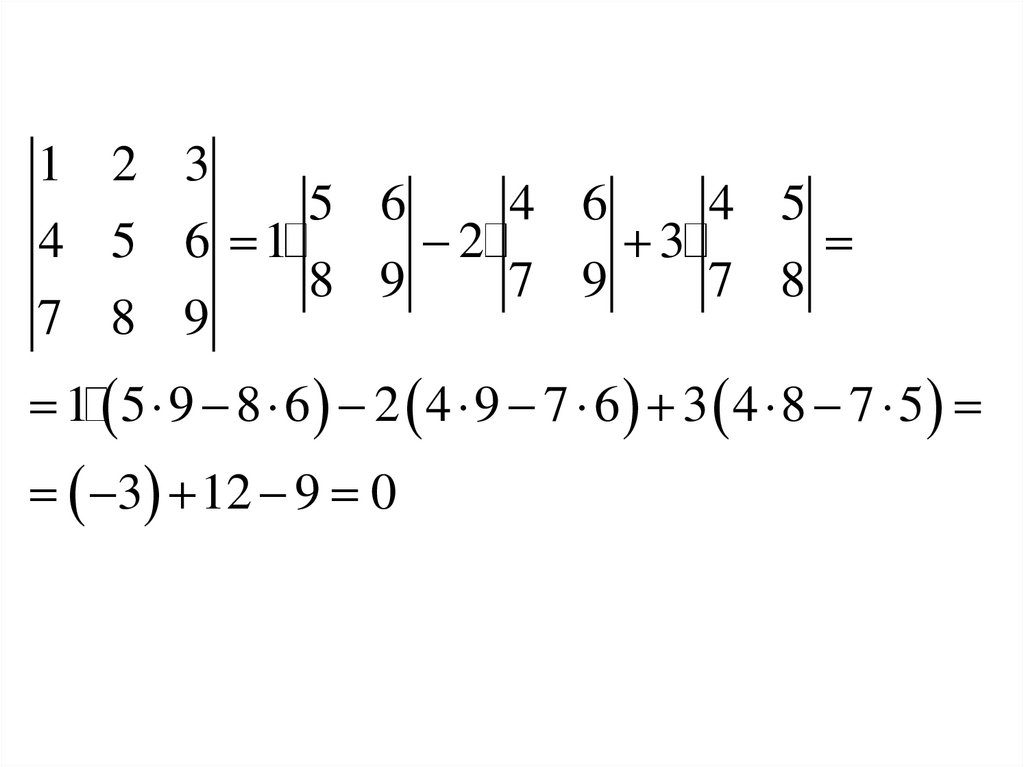



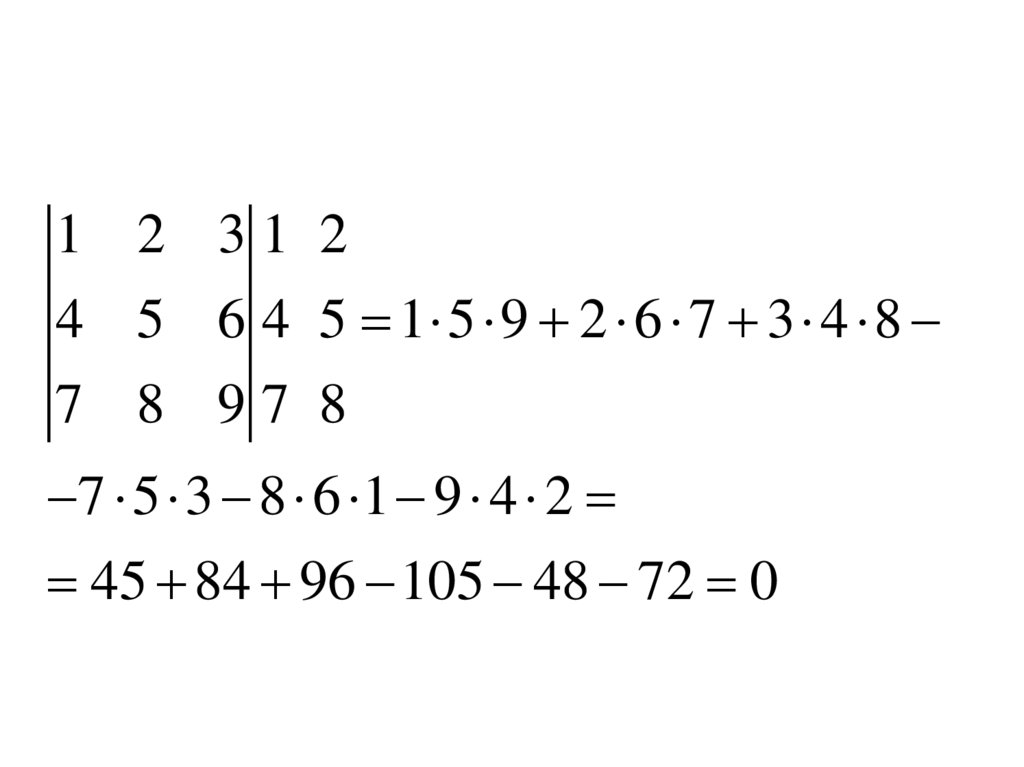



 Математика
Математика








