Числовые промежутки

1.

Тема урока:
Числовые
промежутки

2.

Сегодня мы узнаем:
- Что такое числовые промежутки;
- Виды числовых промежутков;
- Как выглядит геометрическая модель
числового промежутка;
- Как записать аналитическую модель
числового промежутка…

3.

Определение
Множество всех чисел,
удовлетворяющих
данному условию,
называется числовым
промежутком

4.

Таблица числовых промежутков
Неравенство, задающее
числовой промежуток
(аналитическая модель)
Обозначение и
название числового
промежутка
Изображение числового
промежутка на
координатной прямой
(геометрическая модель)

5.

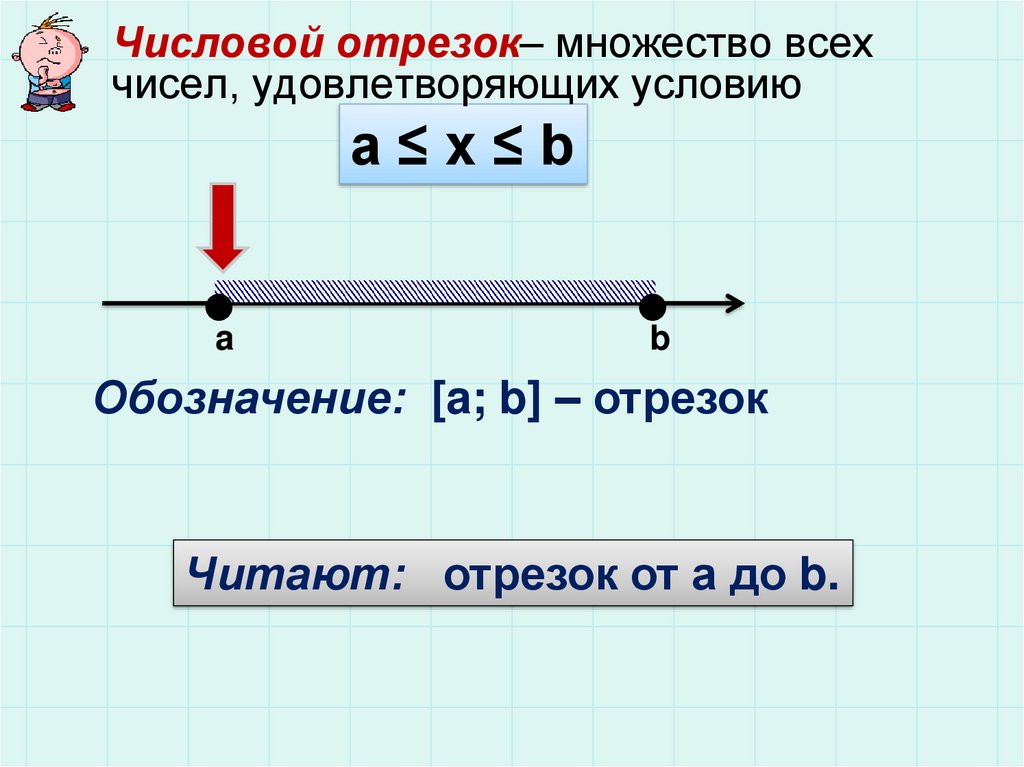
Числовой отрезок– множество всех
чисел, удовлетворяющих условию
а≤x≤b
a
b
Обозначение: [a; b] – отрезок
Читают: отрезок от а до b.

6.

Интервал – множество всех чисел,
удовлетворяющих условию
а<x<b
a
b
Обозначение: (a; b) – интервал
Читают: интервал от а до b.

7.

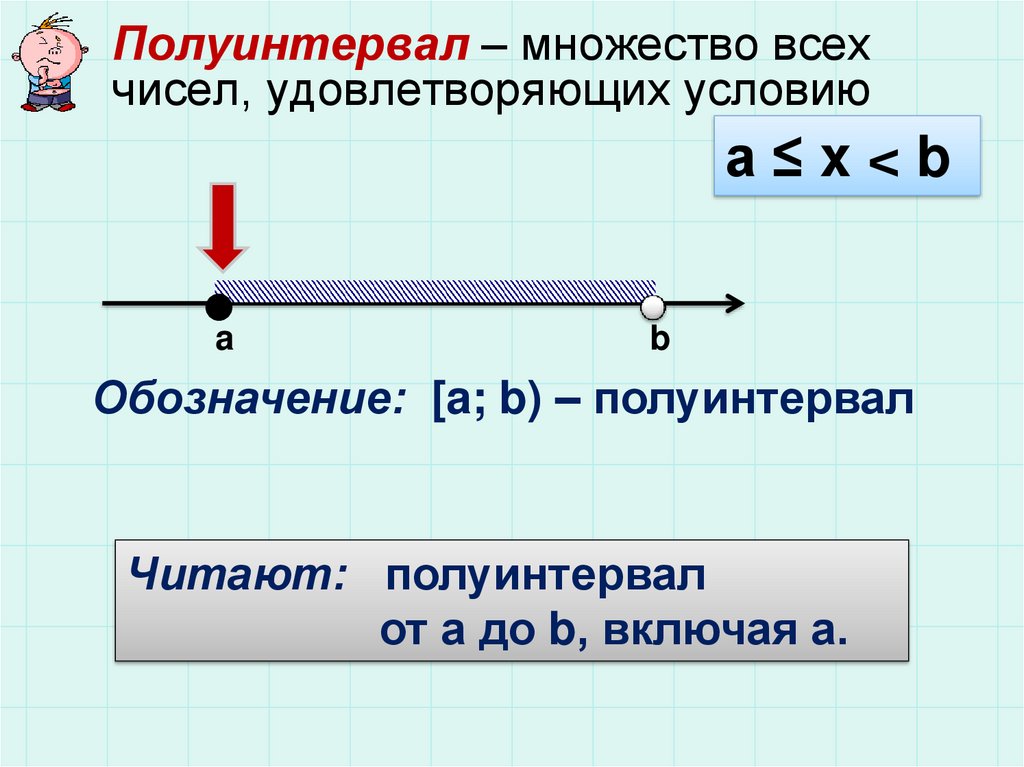
Полуинтервал – множество всех
чисел, удовлетворяющих условию
а≤x<b
a
b
Обозначение: [a; b) – полуинтервал
Читают: полуинтервал
от а до b, включая а.

8.

Полуинтервал – множество всех
чисел, удовлетворяющих условию
а<x≤b
a
b
Обозначение: (a; b] – полуинтервал
Читают: полуинтервал
от а до b, включая b.

9.

Числовой луч – множество всех
чисел, удовлетворяющих условию
x≥а
a
Обозначение: [a; +∞) – числовой луч
Читают: числовой луч от а до
плюс бесконечности.

10.

Открытый числовой луч – множество всех
чисел, удовлетворяющих условию
x>а
a
Обозначение: (a; +∞) – открытый
числовой луч
Читают: открытый числовой
луч от а до плюс бесконечности.

11.

Числовой луч – множество всех
чисел, удовлетворяющих условию
x≤а
a
Обозначение: (-∞;а] – числовой луч
Читают: числовой луч от минус
бесконечности до а.

12.

Числовой луч – множество всех
чисел, удовлетворяющих условию
x<а
a
Обозначение: (-∞;а) – открытый
числовой луч
Читают: открытый числовой
луч от минус бесконечности до а.

13.

Множество действительных чисел
(х -любое число)
(-∞;+∞) - интервал
Числовой промежуток от -∞ до +∞

14.

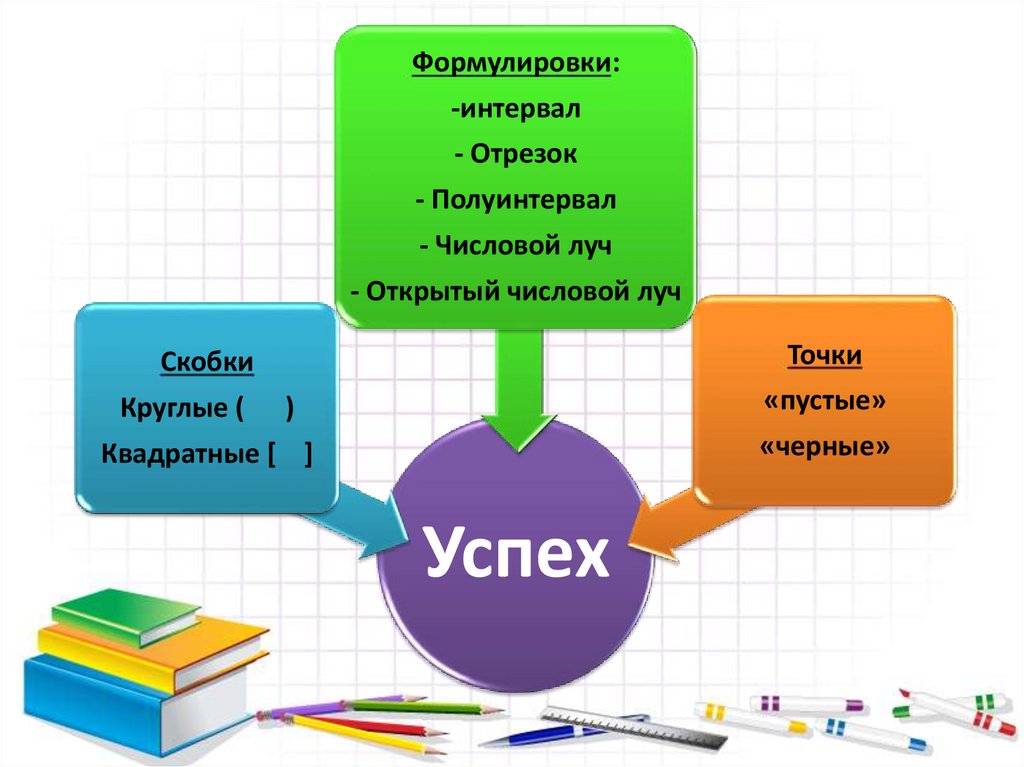
Формулировки:
-интервал
- Отрезок
- Полуинтервал
- Числовой луч
- Открытый числовой луч
Точки
Скобки
Круглые (
«пустые»
)
«черные»
Квадратные [ ]
Успех

15.

Закрепление:

16.

Назовите промежутки, изображенные
на рисунке
-3
12
-8
-8,4
1,8
67

17.

6
- 42
25
-2,3
32
0

18.

Изобразите промежутки на координатной
прямой
[ -3;7);
[8;21];
(2;+∞)
(-∞; 12];
(-1; 3)
(-∞; +∞)
(4;+∞)

19.

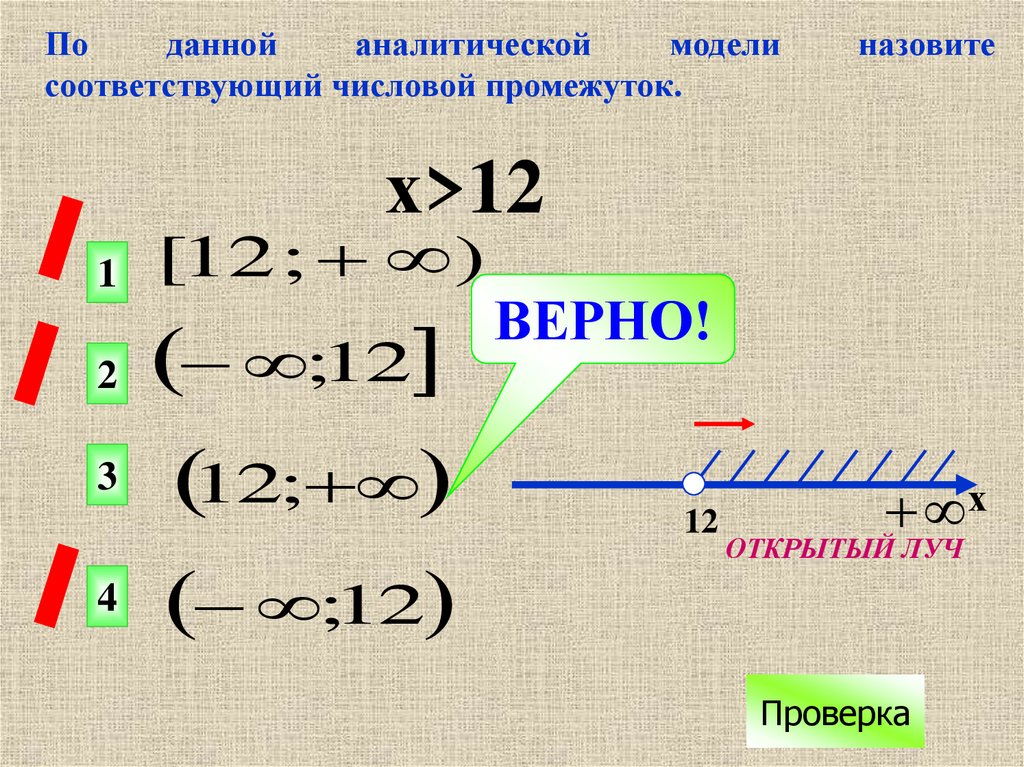
По
данной
аналитической
модели
соответствующий числовой промежуток.
назовите
х>12
1
[12 ; )
2
;12
3
4
12;
;12
ВЕРНО!
12
х
ОТКРЫТЫЙ ЛУЧ
Проверка

20.

По данной аналитической модели назовите соответствующий
числовой промежуток.
-1<х<8
1
2
3
4
1;8
1;8
1;8
8; 1
ВЕРНО!
-1 ИНТЕРВАЛ
8
Проверка
х

21.

По данной аналитической модели назовите соответствующий
числовой промежуток.
х≤-7
1
[ 7 ; )
2
; 7
3
4
; 7
7;
ВЕРНО!
ЛУЧ
-7
Проверка
х

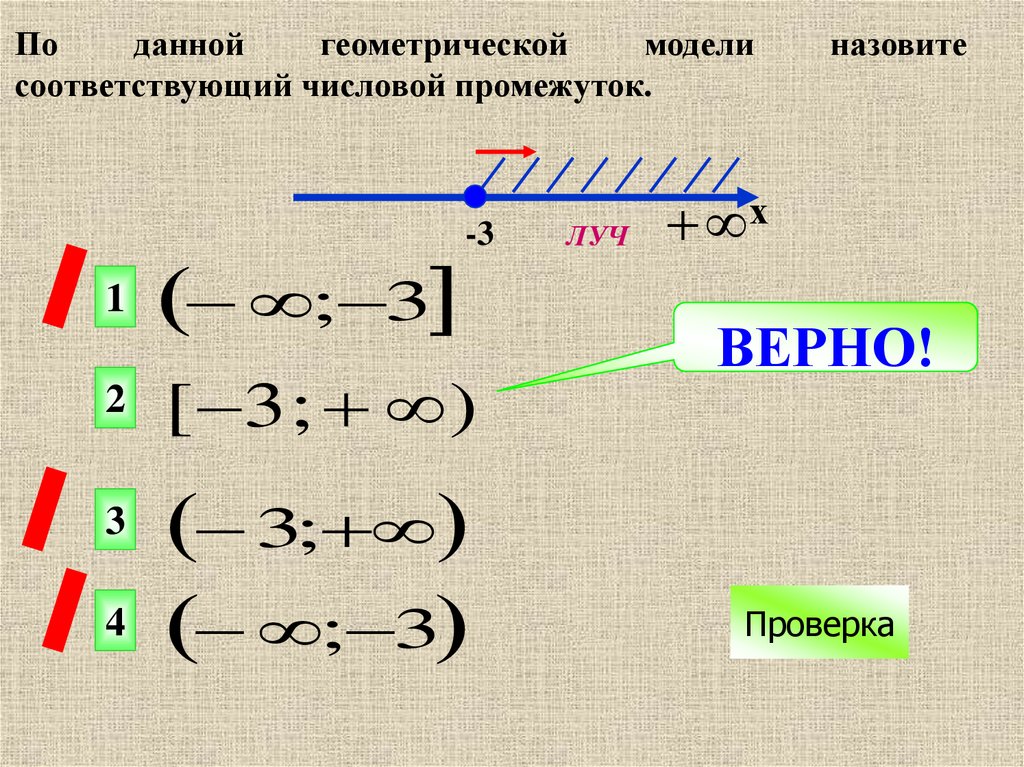
22.

По
данной
геометрической
модели
соответствующий числовой промежуток.
-3
1
; 3
2
[ 3 ; )
3
4
3;
; 3
ЛУЧ
назовите
х
ВЕРНО!
Проверка

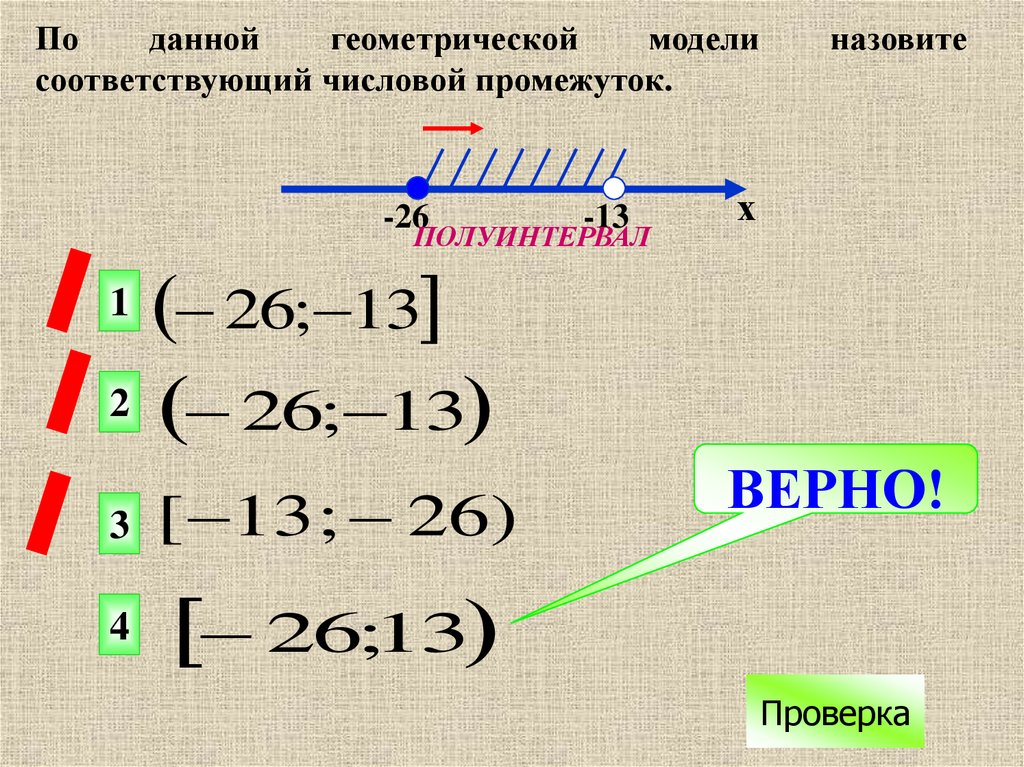
23.

По
данной
геометрической
модели
соответствующий числовой промежуток.
-26
-13
ПОЛУИНТЕРВАЛ
назовите
х
26; 13
2 26; 13
1
3
[ 13 ; 26)
4
26;13
ВЕРНО!
Проверка

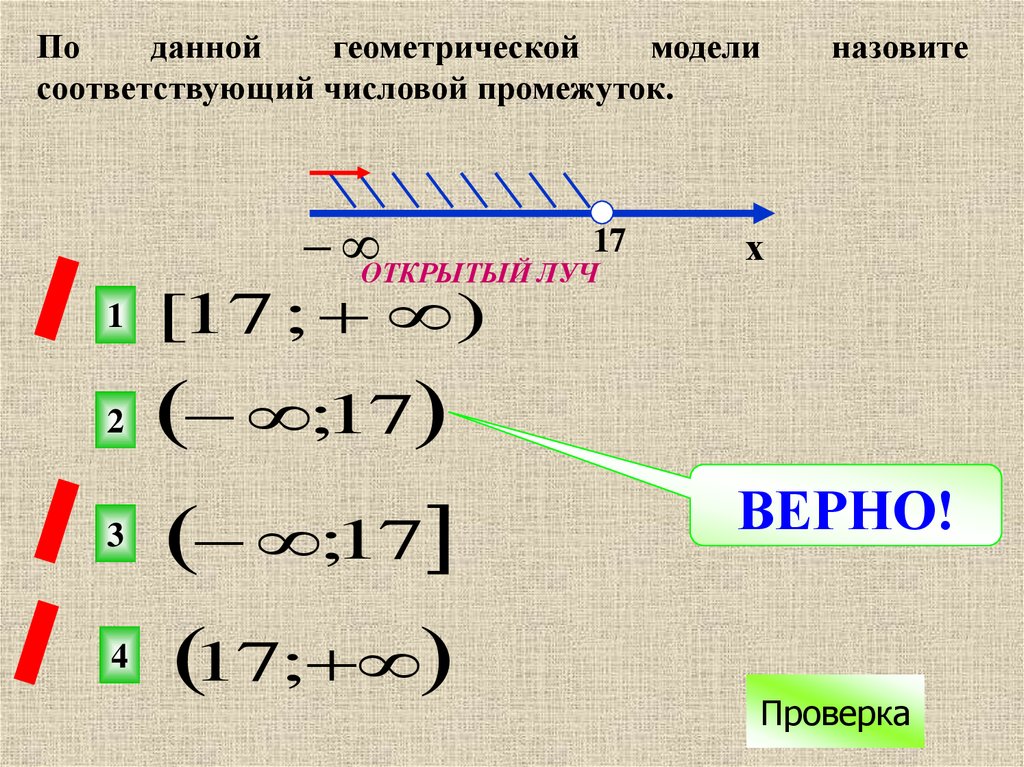
24.

По
данной
геометрической
модели
соответствующий числовой промежуток.
ОТКРЫТЫЙ ЛУЧ17
1
[17 ; )
2
;17
3
;17
4
17;
назовите
х
ВЕРНО!
Проверка

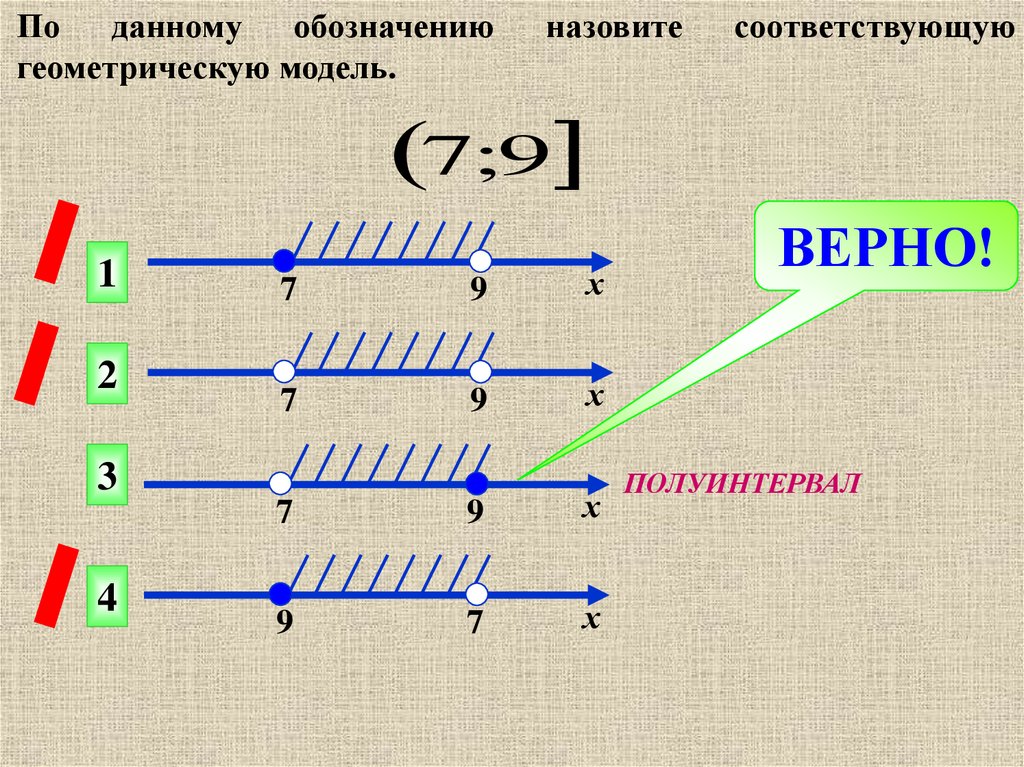
25.

По данному обозначению
геометрическую модель.
назовите
соответствующую
7;9
1
2
7
9
х
7
9
х
3
4
7
9
х
9
7
х
ВЕРНО!
ПОЛУИНТЕРВАЛ

26.

По данному обозначению
геометрическую модель.
назовите
соответствующую
8;19
1
2
3
4
ВЕРНО!
19
8
х
8
19
х
8
19
х
8
19
х
ОТРЕЗОК

27.

По данному обозначению
геометрическую модель.
назовите
соответствующую
; 8
1
ВЕРНО!
х
-8
2
-8
х
-8
х
3
4
-8
х
ОТКРЫТЫЙ ЛУЧ

28.

Домашнее задание
п.33(таблица)
№№ 814,815, 816