Похожие презентации:
График функции. Различные способы построения графиков функций
1. График функции. Различные способы построения графиков функций.
2.
Изучение действий функций ипостроение их графиков
является важным разделом
математики.
Свободное владение техникой
построения графиков часто
помогает решить многие
задачи и порой является
единственным средством их
решения.
3. Цель: повторить известные и изучить новые способы построения графиков и их применение.
План:1)Построение графиков путём их
преобразования;
2)Особые случаи построения графиков;
3)«Полезные» графики;
4)Применение графиков к решению
заданий с параметрами
*
4.
Функцией называется отображение числового множестваX на числовое множество Y, при котором каждому
значению х из области определения D{x) (x принадлежит
D(x) С X) ставится в соответствие единственное у € Е С Y
(Е - область значения функции у =f (x)).
График функции у = f(x) - это множество точек плоскости с
координатами (x;у), у которых абсциссы х - есть
допустимые значения аргумента, а ординаты у соответствующие им значения функции.
5. 1) Построение графиков функций, прием их преобразования.
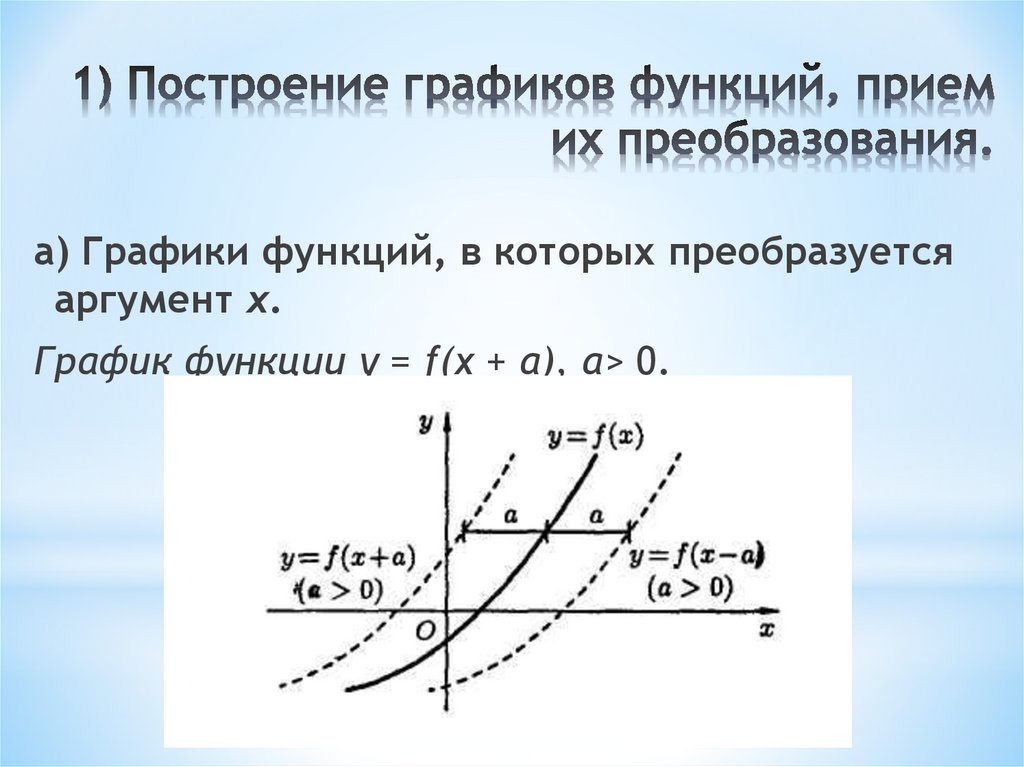
а) Графики функций, в которых преобразуетсяаргумент х.
График функции у = f(x + а), а> 0.
6.
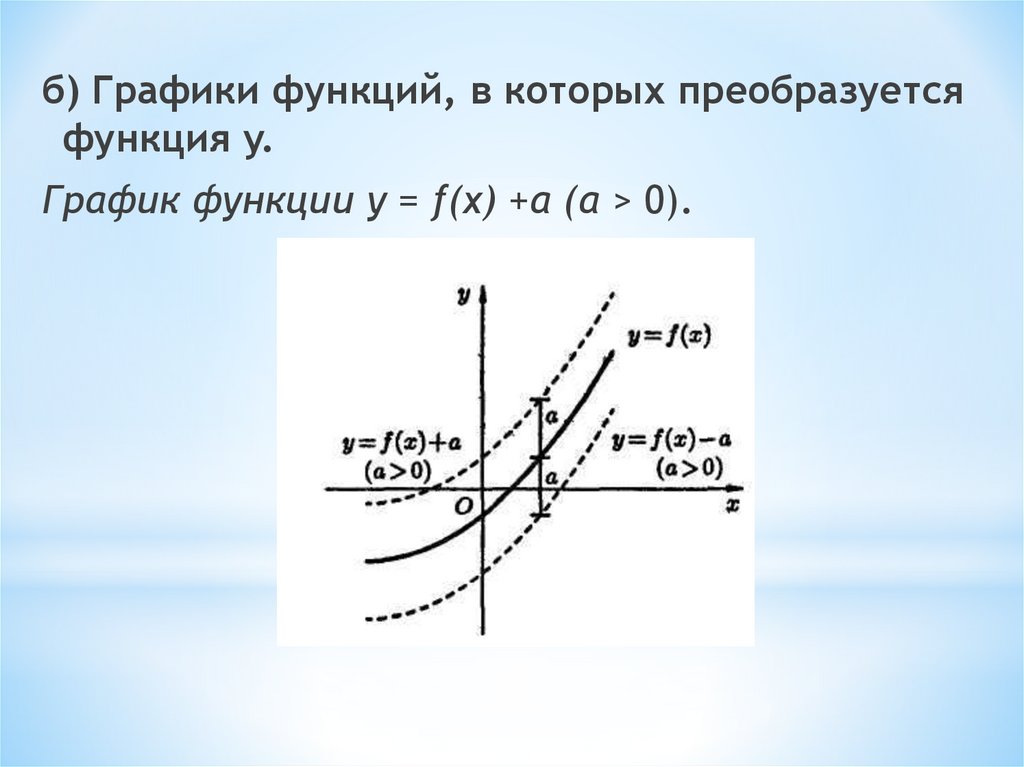
б) Графики функций, в которых преобразуетсяфункция y.
График функции у = f(x) +а (а > 0).
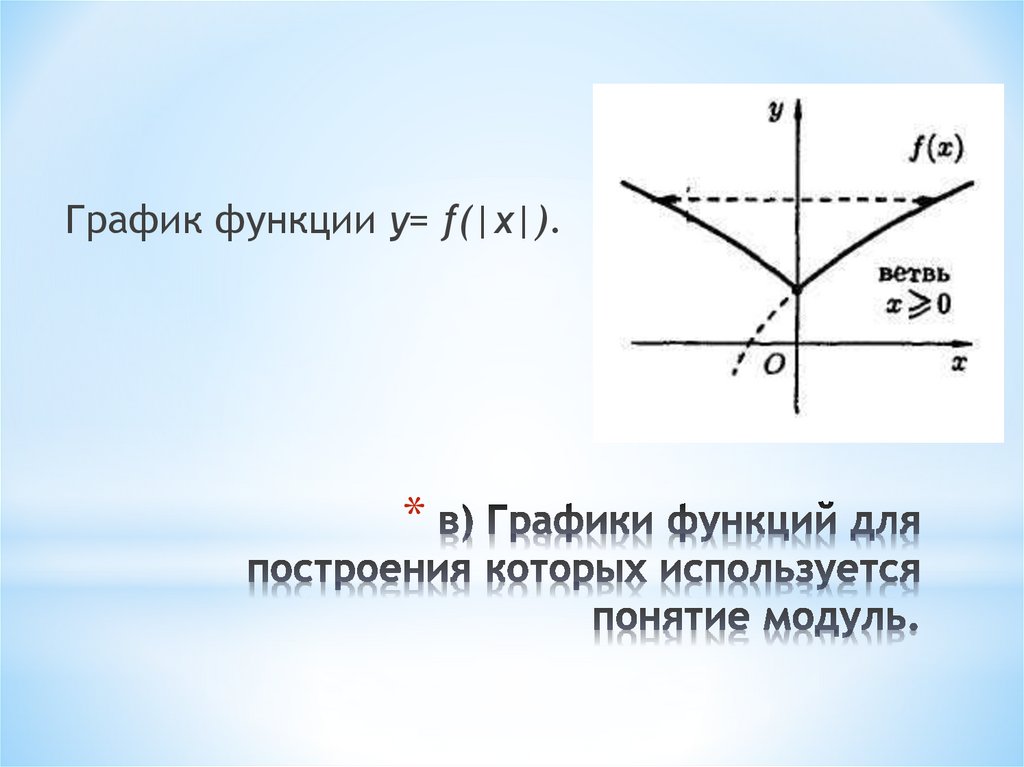
7. в) Графики функций для построения которых используется понятие модуль.
График функции у= f(|x|).*
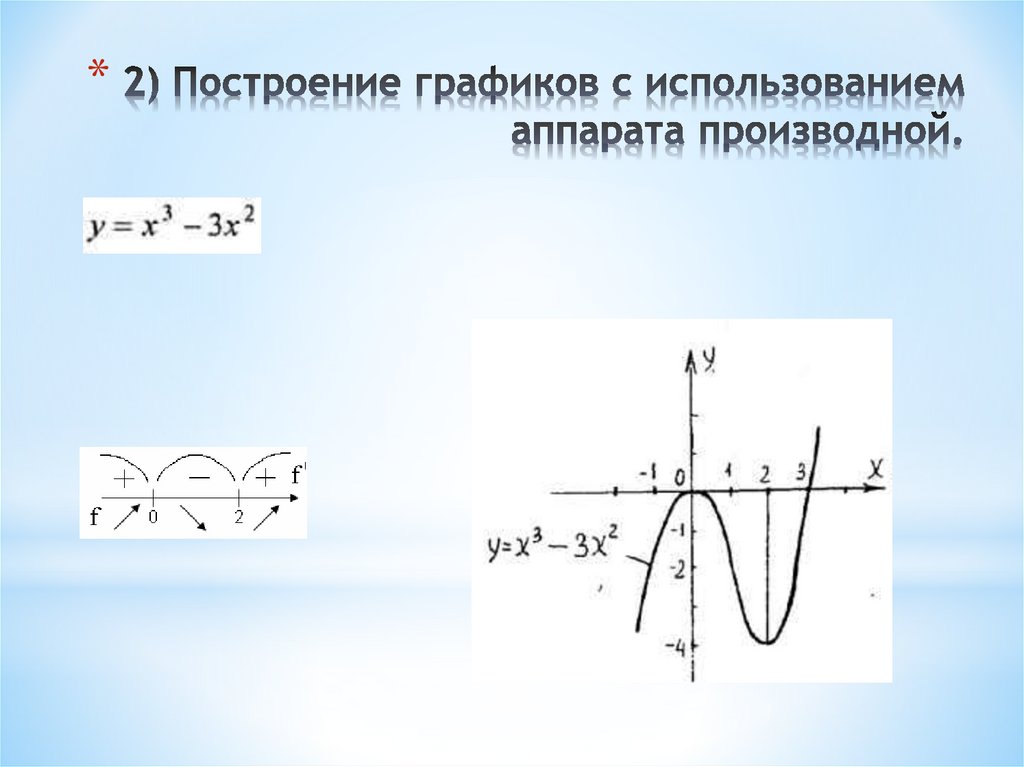
8. 2) Построение графиков с использованием аппарата производной.
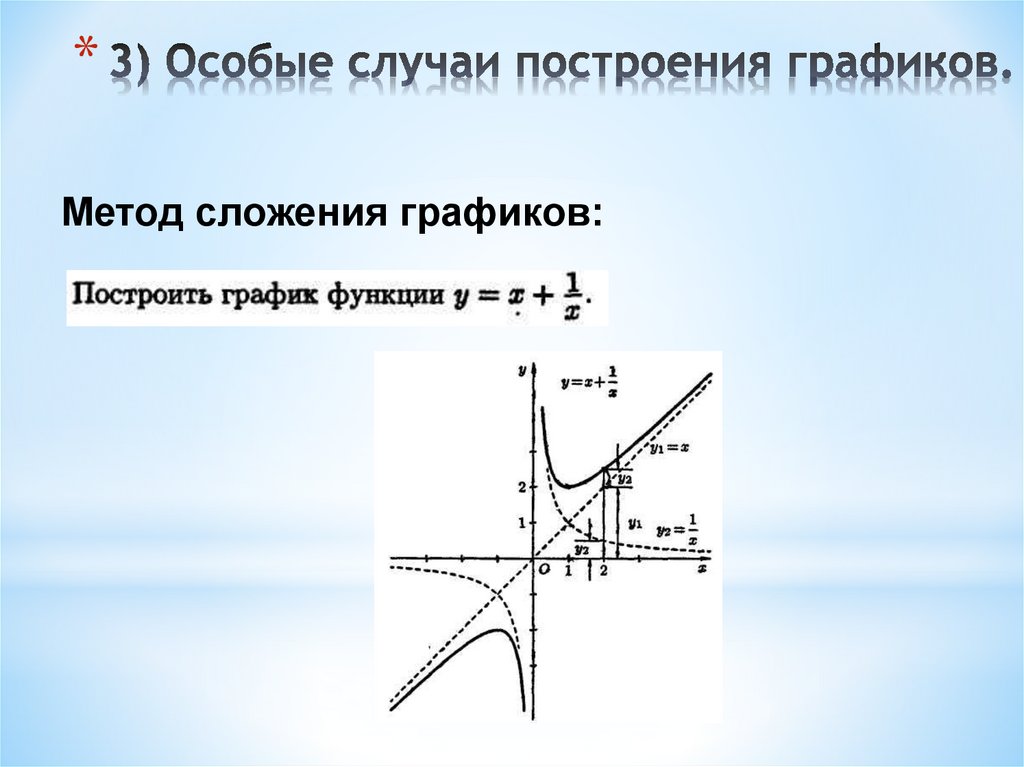
*9. 3) Особые случаи построения графиков.
*Метод сложения графиков:
10. Метод деления (умножения) графиков:
*11.
«Полезные» функции.«Корыто»
12.
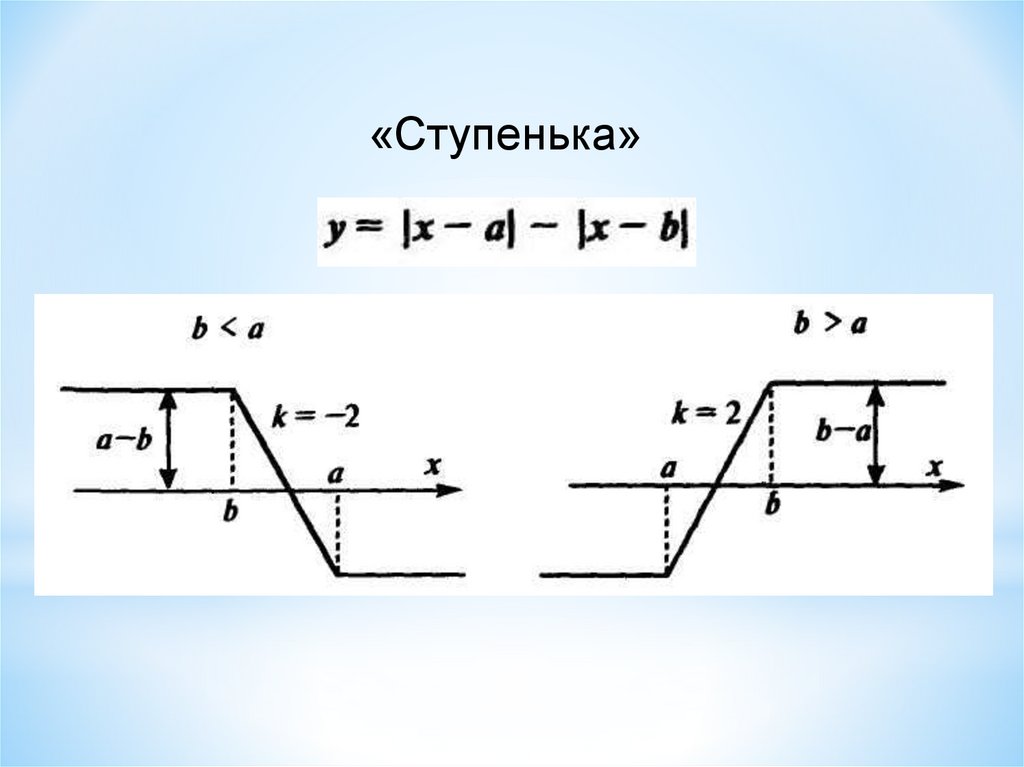
«Ступенька»13.
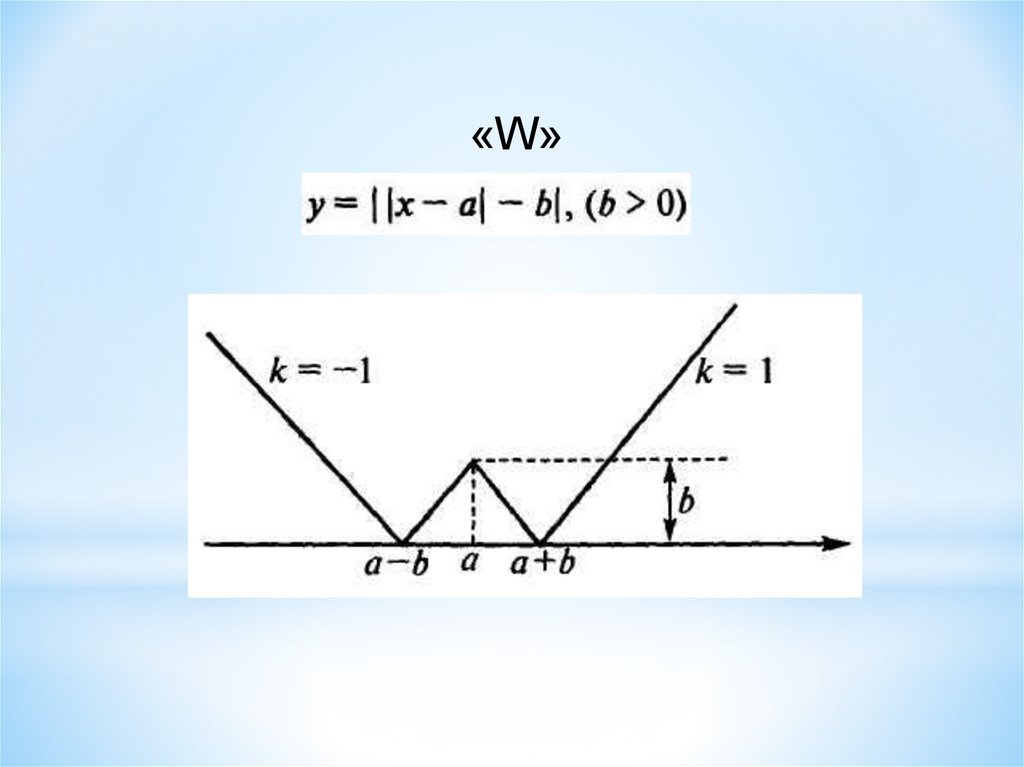
«W»14.
«Волна»15.
«Близнецы»16.
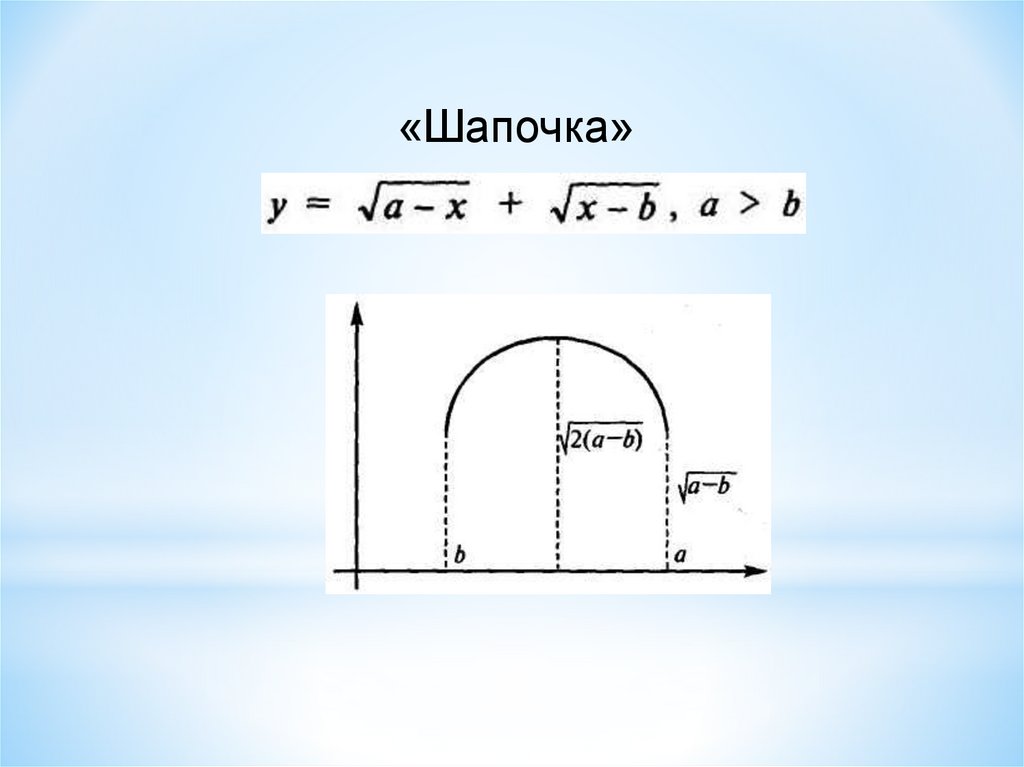
«Шапочка»17.
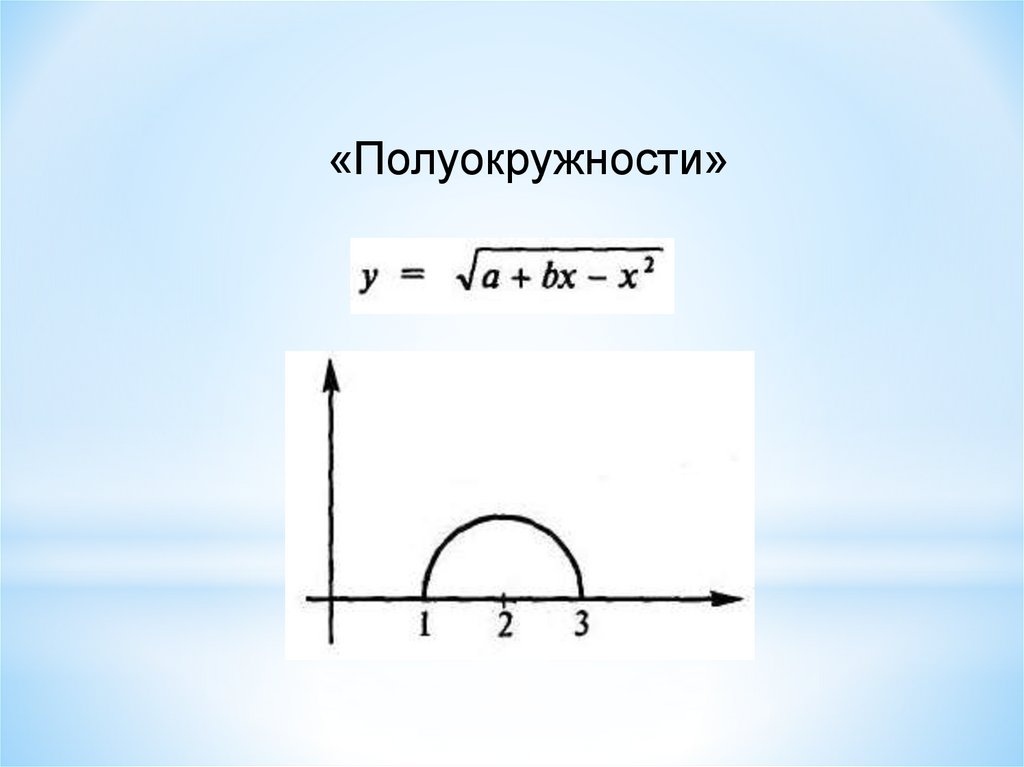
«Полуокружности»18.
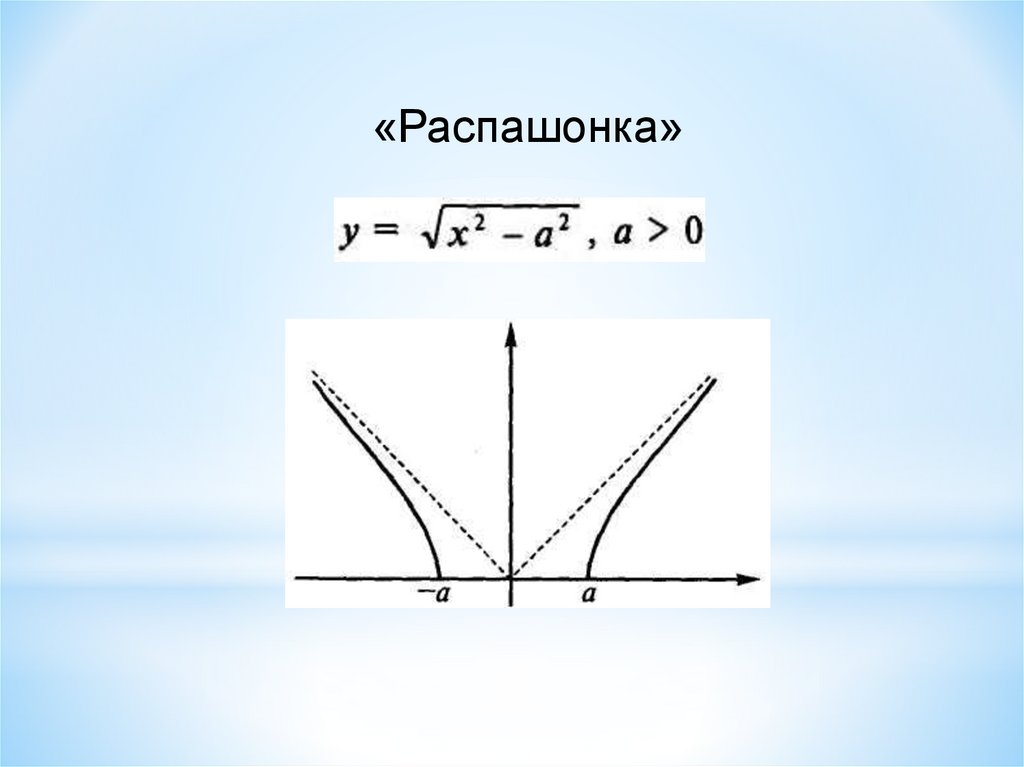
«Распашонка»19.
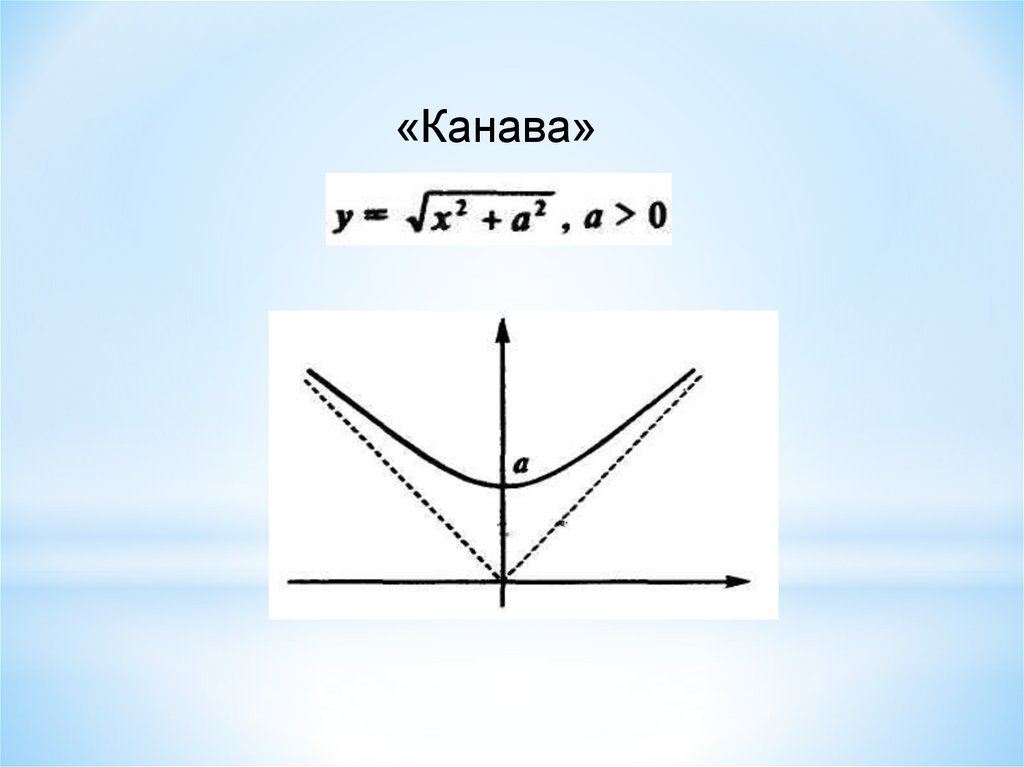
«Канава»20.
«Горка»21.
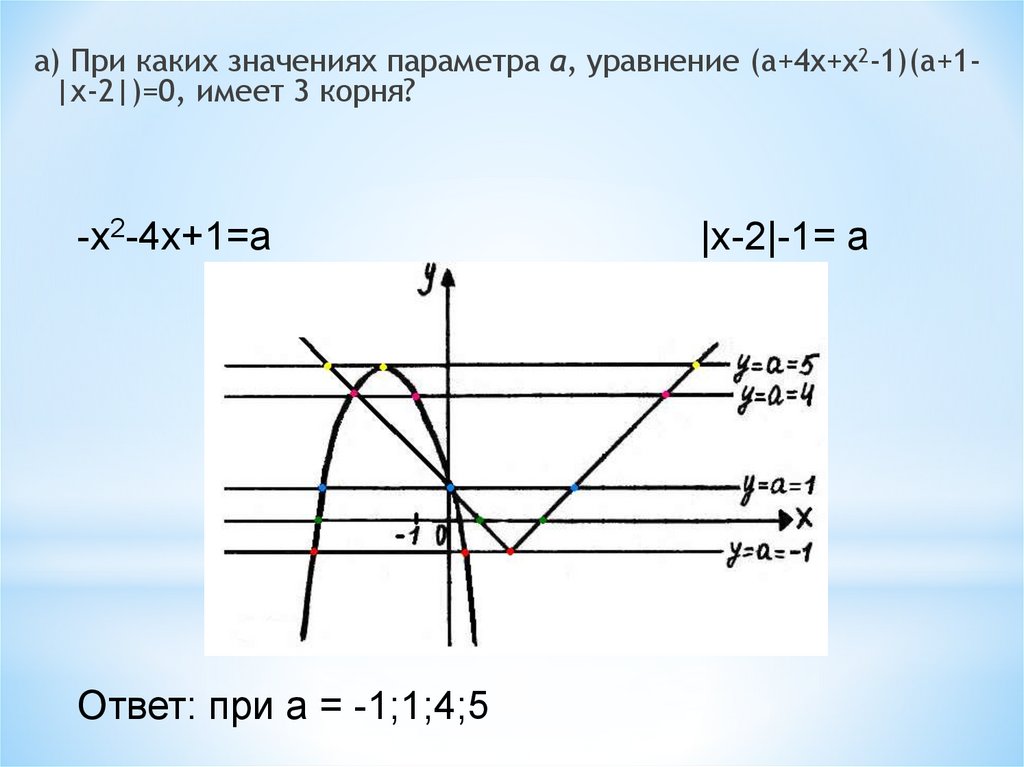
а) При каких значениях параметра a, уравнение (a+4x+x2-1)(a+1|x-2|)=0, имеет 3 корня?-x2-4x+1=a
Ответ: при a = -1;1;4;5
|x-2|-1= a
22.
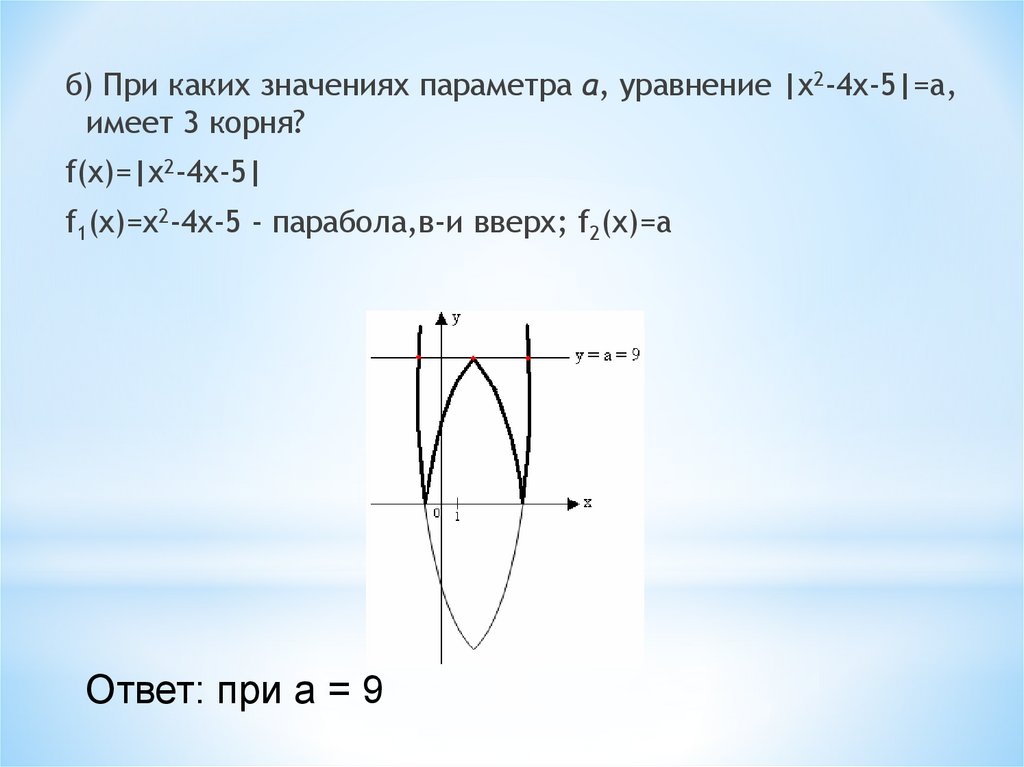
б) При каких значениях параметра a, уравнение |x2-4x-5|=a,имеет 3 корня?
f(x)=|x2-4x-5|
f1(x)=x2-4x-5 - парабола,в-и вверх; f2(x)=a
Ответ: при a = 9









 Математика
Математика








