Вся геометрия 9 класса в кратком изложении (к учебнику Л.С. Атанасяна и др.)

1.

Памятка
Вся геометрия
9 класса в кратком изложении
(к учебнику Л.С. Атанасяна и др.)

2.

Вся геометрия
o·Ã¶ÉÁ·
9 класса в кратком изложении
(к учебнику Л.С. Атанасяна и др.)
СОДЕРЖАНИЕ
Скалярное произведение векторов . . . . . . . . 45
Скалярное произведение векторов,
заданных в координатах . . . . . . . . . . . . . . . . . . . . 45
Разложение вектора по двум
G G
неколлинеарным векторам a и b. . . . . . . . . 1
Декартовы координаты на плоскости . . . . . . 1
Действия над векторами . . . . . . . . . . . . . . . . . . . 2
Уравнение прямой в общем виде
ax + by = c, где a,b,c – числа . . . . . . . . . . . . . 45
Расстояние между двумя точками . . . . . . . . . . 2
Многоугольники. Длина окружности.
Площадь круга . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
Уравнение окружности . . . . . . . . . . . . . . . . . . . . . 2
Формулы для правильного многоугольника 56
Координаты середины отрезка . . . . . . . . . . . . . 2
Sin A cos A tg A где 0° + A + 180° . . . . . . . . . . . 3
Движение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
G. . . . . . . . 2
Нахождение координат вектора AB
Многогранники . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
Тела вращения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
Теорема синусов и косинусов . . . . . . . . . . . . . . . 3
G
Разложение вектора по двум неколлинеарным векторам G
a иb
A
F
B
G = 2a +b
OA
G G
С
G
G
G = 0 a – 2 b
OC
3
G
G
G
OF = 1,5 a – 0 b
G
G
b
O
p ;:987 654382
G
G
G
p = x a + y b , 105 x и y – ./-;,
G
p 2,+;,1,53-* 50/)-365))(' -&8-898'
G= –G
OE
a+2 b
3
G
E
D
G = 1,5 a – b
OB
G G
G
a
Декартовы координаты на плоскости
y
A
G
a
b
G
j
G
i
O
N
i / j 48820/),3)(5 654382(
IGi I IGj
G
a{3;4}
G
G
G
G
a = 3 i 4 j
G
G
G
i 2 j
a = √ 3 2 + 4 2 = 5
IG
G = √ (-5) 2 + 2 2 = √ 29
I b
ON = 3
IG
IG
d = √ 4 2 + (- 2 ) 2 = √ 20
G
IOM = 4
B = √ 68
IAG
G
C
I D = √ 37
G
x
d
C
G G
Длина вектора
G
O
N { 0 ; -3 }
M
G
G
с
Разложение
вектора
b { -5 ; 2 }
G
B
Координаты
вектора
D
d { 4 ; -2 }
G
O
M{4;0}
G
AB { -8 ; -2 }
G
C
D{6;1}
b = -5
G
G
O
N = -3 j
G
G
G
d = 4 i 2 j
G G
G G
G
A
B = -8 i 2 j
G G
G
C
D = 6 i j
OM = 4 i
I
G
a{x;y} ; G
a = √ x2 + y2

3.

Действия над векторами
G
G
a { x1 ; y1 } = x1G
i + y1 j
G
G
G
b { x2 ; y2 } = x2 i + y2 j
G G
G
G
a + b = ( x1+x2 ) i ( y1+y2 ) j
G G
G
G
a - b = ( x1-x2 ) i ( y1-y2 ) j
G
k a { kx1 ; ky1 } 105 k — ./-;8
G
Нахождение координат вектора AB
"%-3! О ),.,;8 48820/),3
B { x2 ; y2 }, A { x1 ; y1 }
G
G
G
98+),./' OB = G
b , OA = a
G= ( G
G
810, AB
b — a ) {x2 — x1 ; y2 — y1}
Расстояние между двумя точками
A { x1 ; y1 }
B { x2 ; y2 }
G = √ (x2 — x1 )2 +(y2 — y1 )2
AB = IAB
Уравнение окружности
OM = R = √ (x — a ) 2 + (y — b ) 2
M (x ; y)
R
O (a ; b)
(x — a ) 2 + (y — b ) 2 = R 2
x 2 + y 2 = R 2
%2,6)5)/5 842%$)8-3/ - #5)
328' 6 38.45 (a ; b) 2,0/%-, R
%2,6)5)/5 842%$)8-3/ - #5)328' 6
),.,;5 48820/),3 (0 ; 0) 2,0/%-, R
Координаты середины отрезка
y
A (x1 ; y1)
С (x ; y)
B (x2 ; y2)
O
A1
С1
B1
&8 35825'5 ,;5-,
x
x x1 + x2
y y1 + y2
2

4.

Sin A cos A tg A где 0° + A + 180°
y
(0 ; 1)
r=1
1. A 8-32(7 %18; 3810, sin A = y = y ; cos A = x = x ; tg A
1
1
M (x ; y)
"8;%./;/ 82'%;( sin A y
cos A x
tg A sin A
cos A
y
A
O x
(-1 ; 0)
(1 ; 0) x
2. &2505;/' +),.5)/* sin A, cos A, tg A <3/'/ 82'%;,'/
0;* ;:9818 %1;, A &2/),0;5$,>518 8325+4%
sin 0o 0
cos 0o 1
tg 0o 0
sin 90o 1
cos 90o 0
tg 90o не имеет
смысла
sin A
cos
A
3. 82'%;( &2/6505)/* "8-3,2,735-!
084,+,3! <3/ 82'%;( /-&8;!+%* .5235$/
cos A
sin A
sin (180o A sin A
cos (180o A cos A
sin (90o A
sin 180o 0
cos (90o A
cos 180o 1
tg 180o 0
4. "8;%842%$)8-3! *6;*53-* 0%187 842%$)8-3/ x 2 + y 2 = 1
;:9818 %1;, A &2/),0;5$,>518 8325+4%
>
sin 2 A + cos 2 A = 1 6(&8;)*53-* 0;*
Эта формула называется основным
тригонометрическим тождеством
Теорема синусов и косинусов
Теорема синусов:
A
a = b = c = 2R
sinA sinB sinC
c
b
B
a
D;* 084,+,35;!-36, /-&8;!+86,3! 82'%;(
s6 = 21 ab sinC = 21 ac sinB = . . . , , 3,4$5 +,0,.% E
C
Теорема косинусов:
a 2 = b 2 + c 2 – 2 bc cosA
Доказательство
y
С (b cosA ; b sinA)
a
b
CB2 = ( b cosA – c)2 + (b sinA) 2 = b2cos2A – 2bc cosA + c2 + b2sin2A =
= b2( cos2A+ sin2A) + c2 – 2bc cosA ,
c
A (0 ; 0)
F,&/G5' 46,02,3 2,--38*)/* '5$0% 38.4,'/ /
48820/),3( 48382(H /+65-3)(
B (c ; 0)
x
=1
3
ч.т.д.

5.

Скалярное произведение векторов
Скалярное произведение векторов
широко применяется в физике
G G
Определение: G
% 8 G
b = | a | 8 | b | 8 '03 A
G
a
G G
a.G
1. G
b , то % 8 b = 0
G
a 8 G
a
2.
A
G
F
=
Скалярный квадрат вектора G
a
G
b
F – сила
G
2
|G
a | 8 |G
a | = |G
a|
J
M
G – перемещение
MN
A – работа
N A = |G
F | 8 |MN | 8 '03 J
G
Скалярное произведение векторов, заданных в координатах
В
G
a { x1 ; y1 } ; G
b { x2 ; y2 }
G
b
A
О
A
G
a
Доказательство
G { x2 – x1 ; y2 – y1 } ; |AB
G|2 = ( x2 – x1)2 + ( y2 – y1)2
3. AB
1. По теореме косинусов
AB 2 = ОB 2 + ОА2 – 2ОВ OA'03 A
2.
G|2 =
|AB
Доказать: G
a G
b = x1x2 + y1y2
2
2
G
2
2
|G
b |2= x2 + y2 ; | a |2= x1 + y1
G2
GG
|G
b |2 + | a | – 2 b a
Следствие 1
b ? x1 x2 + y1y2 = 0
2
2
2
2
4. G
% 8 G
b = 1 (x2 + y2 + x1 + y1 – (x2 – x1)2 – ( y2 – y1)2) =
= x1x2 + y1y2
ч.т.д.
Следствие 2
G
a .G
'03 A
x1 x2 + y1y2
x12 + y12 x22 + y22
Свойства
G GG GG
a2 *0
1. G
3. ( G
a +G
b)с = a с + b с
GG
G G
GG
2. G
a G
b = b a 4. (k a ) b = k ( a b )
Уравнение прямой в общем виде ax + by = c, где a,b,c – числа
1 При b " 0 ; y = – a x + c , приняв – a = k , c = l , получим y = kx + l
b
)
y1
1;
(x
A
A
B (x2 ; y2)
y2 – y1
x2 – x1
y=
kx
+
l
A
O
x
b
b
Выясним геометрический смысл коэффициента k.
y2 – y1
k = tg A – называется угловым коэффициентом
1. tg A ______
x2 – x1
k ( 0 (A – острый угол)
2. y2 = kx2 + l
k ) 0 (A – тупой угол)
y1 = kx1 + l
{
y2 – y1 = k (x2 – x1)
y2 – y1
k ______
x2 – x1
l – ? ; x = 0 , тогда y = l
(0 ; l ) – точка пересечения прямой y = kx + l
с осью 06
Рассмотрим частные случаи:
1. b " 0 ; a " 0 ; c = 0, тогда y = kx, график проходит через начало координат.
2. b " 0 ; a = 0 ; c = 0, тогда y = 0 – уравнение оси 05
3. b " 0 ; a = 0 ; c " 0, тогда y = l – уравнение прямой, параллельной оси 05
b = 0 ; a " 0 ; c = 0 ; x = 0 – уравнение оси 06
4
5
kx
y=
х=0
2 b = 0 ; a " 0 ; c " 0 ; x = c – уравнение прямой, параллельной оси 06
a
y
y=l
х = ac
b
y
O
y=0
x

6.

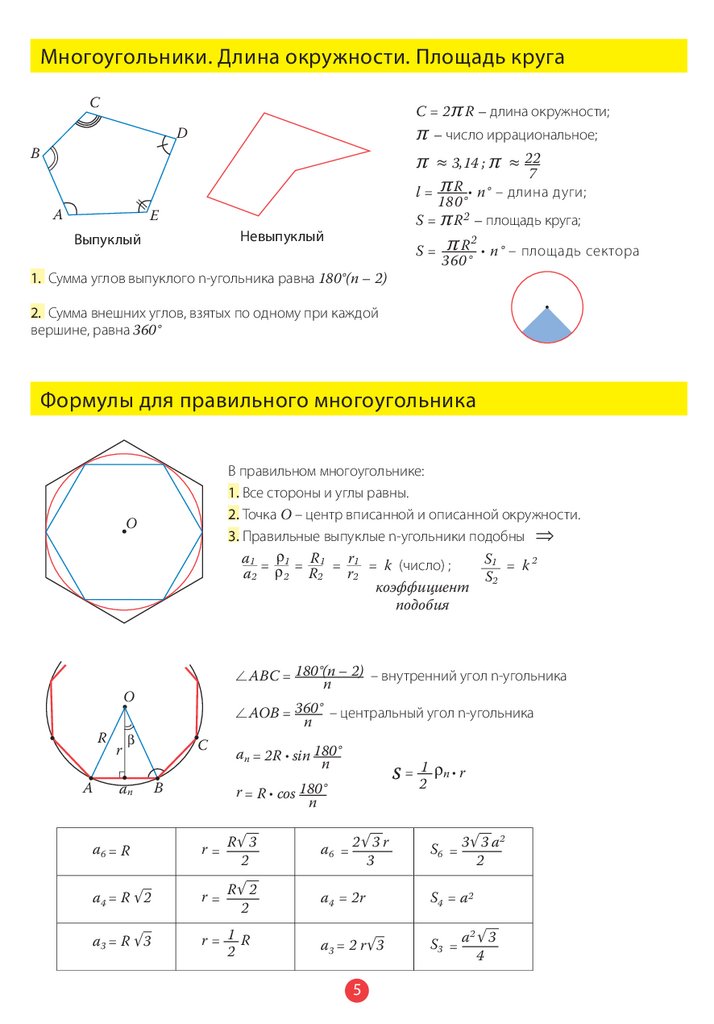
Многоугольники. Длина окружности. Площадь круга
C
С = 2 π R – длина окружности;
π – число иррациональное;
π ≈ 3,14 ; π ≈ 22
7
l = π R n° – длина дуги;
D
B
A
180°
S = π R 2 – площадь круга;
E
Невыпуклый
Выпуклый
S=
1. Сумма углов выпуклого n-угольника равна 180°(n – 2)
π R 2 n° – площадь сектора
360°
2. Сумма внешних углов, взятых по одному при каждой
вершине, равна 360°
Формулы для правильного многоугольника
В правильном многоугольнике:
1. Все стороны и углы равны.
2. Точка О – центр вписанной и описанной окружности.
3. Правильные выпуклые n-угольники подобны >
R1 ___
r1 = k (число) ; ___
S1 = k 2
1 = ___
a___
= R1 = ___
a2 R2 R2
r2
S2
коэффициент
подобия
O
2 ABC = 180°(n – 2) – внутренний угол n-угольника
n
O
R
A
r
2 AOB = 360° – центральный угол n-угольника
n
B
an
C
B
an = 2R 3+/ 180°
n
3 = 21 Rn r
r = R '03 180°
n
2
a6 = R
r = R√ 3
2
a6 = 2√ 3 r
3
S6 = 3√ 3 a
2
a4 = R √ 2
r = R√ 2
2
a4 = 2r
S4 = a2
a3 = R √ 3
r= 1 R
2
a3 = 2 r√ 3
2
S3 = a √ 3
4
5

7.

Движение
Определение
Движение – отображение плоскости на себя, при котором сохраняются расстояния между точками.
Свойства движений
1. Прямая отображается на прямую, луч – на луч, отрезок – на отрезок.
2. Отрезок отображается на равный отрезок, угол – на равный угол, треугольник – на равный ему треугольник.
Примеры движения
1. Осевая симметрия
2. Центральная симметрия
3. Параллельный перенос
4. Поворот
a
O
M N
ОСЕВАЯ СИММЕТРИЯ (Обозначим Sa)
N1 M1
M1
M
N1
M1 N1 = Sa (MN)
Sa (M NN1 M1) = M1 N1NM
Получили ту же фигуру.
В таком случае говорят, что
фигура имеет осевую симметрию.
N
M1
M
N
N1
M M1
N N1
N1
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ (Обозначим S0)
По определению
N1 = S0 (N), так как :
1) O э NN1 ; 2) NO = ON1
M
O
C
B
O
A
Фигуры, обладающие
центральной симметрией
Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм. Прямая
также обладает центральной симметрией, только в отличии от окружности
и параллелограмма, которые имеют
только один центр симметрии, у прямой их бесконечно много.
M1 N1 = Sо (MN)
Sо (ABCD) = CDAB
Получили ту же фигуру.
Данная фигура обладает
центральной симметрией.
M1
N
Фигуры, обладающие осевой
симметрией
По определению
M1 = Sa (M), так как :
1) MM1 . a ; 2) MO = OM1
D
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
M1
G
a
M
N
ПОВОРОТ
N1 Параллельный
перенос задан
вектором G
a
G
a (M) = M1 ;
G
a (N) = N1 ;
G
a (MN) = M1 N1
X
Поворот задан центром
и углом поворота
X G X I , если OX I = OX
2 X IOX = A
XI
6
7
A
т. O – центр
O A – угол поворота

8.

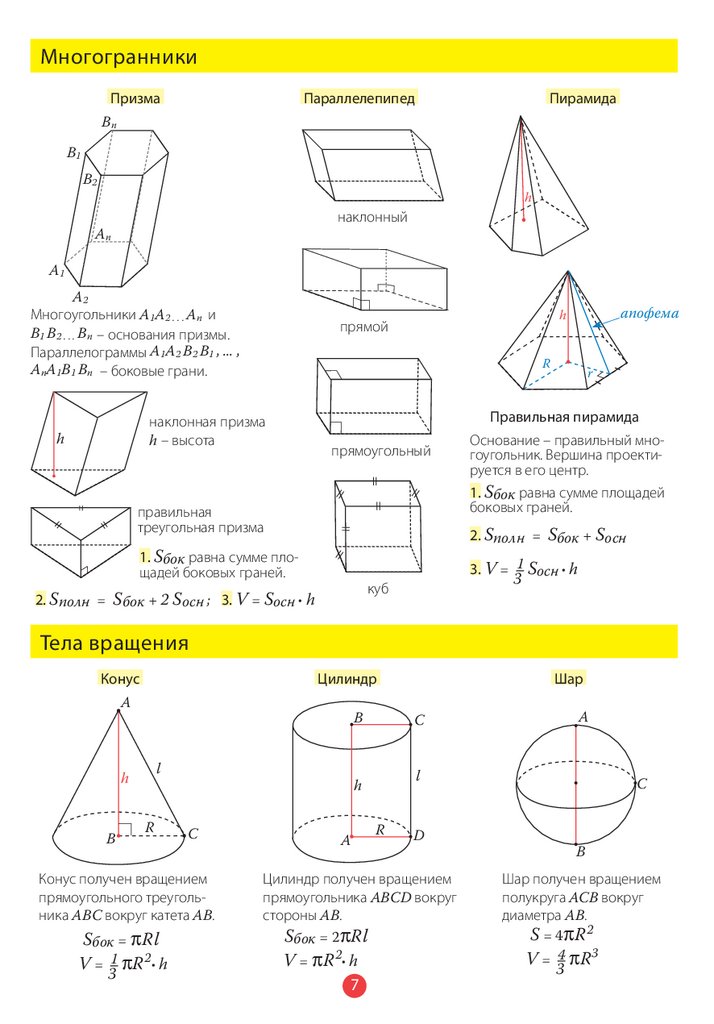
Многогранники
Призма
Параллелепипед
Пирамида
Bn
B1
B2
h
наклонный
An
A1
A2
Многоугольники A1A2 . . . An и
B1 B2 . . . Bn – основания призмы.
Параллелограммы A1A2 B2 B1 , ... ,
AnA1B1 Bn – боковые грани.
R
прямоугольный
правильная
треугольная призма
Основание – правильный многоугольник. Вершина проектируется в его центр.
1. Sбок равна сумме площадей
боковых граней.
2. Sполн =
1. Sбок равна сумме площадей боковых граней.
2. Sполн =
r
Правильная пирамида
наклонная призма
h – высота
h
апофема
h
прямой
3. V = 1 Sосн h
3
куб
Sбок + 2 Sосн ; 3. V = Sосн h
Sбок + Sосн
Тела вращения
Конус
Цилиндр
Шар
A
B
l
h
B
C
Конус получен вращением
прямоугольного треугольника ABC вокруг катета AB.
Sбок = PRl
V = 1 PR 2 h
3
l
h
R
A
R
7
C
D
Цилиндр получен вращением
прямоугольника ABCD вокруг
стороны AB.
Sбок = 2PRl
V = PR 2 h
A
C
B
Шар получен вращением
полукруга ACB вокруг
диаметра AB.
S = 4PR 2
V = 4 PR 3
3

9.

О методе
За основу данного справочного пособия взят авторский метод Гориной Д.А. Он изложен в форме
книжки-раскладушки. Весь учебный материал по
геометрии 9-го класса представлен, как на ладони, и его можно охватить единым взглядом.
Метод Гориной Д.А. позволяет легко освоить
знания по геометрии и прочно укрепить их в памяти. Русунки, графики и цветовое оформление
материала облегчают обучение.
Эффективность данного метода проверена
годами на практике. Пособие предназначено для
учащихся, учителей, родителей.
Горина Д.А. – учитель с многолетним педагогическим стажем. Она преподавала математику во всех параллелях (с 5 по 10 классы), в том числе и в
классах с углубленным изучением математики. Кроме того, она обладает большим опытом работы с трудными учениками. Учитель высшей
категории, отличник народного просвещения, Горина Д.А. имеет награду
Института «Открытое общество» – Грант Сороса.
Об авторе
Пособие, которое вы держите в руках, первоначально я разработала специально для своих учеников, которые с трудом осваивали геометрию по обычным
учебникам. Я решила представить для них учебный материал как можно
доступнее: в сжатой и наглядной форме.
В результате благодаря этому методу моим ученикам было гораздо легче
вспомнить пройденный материал и усвоить новый. Геометрия перестала
быть для них сложным предметом.
Теперь я хочу поделиться со всеми накопленным опытом и искренне верю, что
это пособие поможет любому ученику в освоении геометрии.
Другие
книги
автора
«Вся геометрия 7 класса в кратком изложении»
«Вся геометрия 8 класса в кратком изложении»
cÄƾö d `
ISBN 978-5-9900239-9-4
Горина Д.А., Вся геометрия 9 класса в кратком
изложении – М.: Евробукс, 2009. – 8 с.
© Горина Д.А., 2009
© «Евробукс», 2009