Непрерывные функции

1. Математический анализ

Лекция -3(ю)
Непрерывные функции
1
05.12.2018

2.

Предел функции
Повтор лекции 2
определена
Пример :
f ( x)
3
1
x sin x
в точке x = 0 не определена , но
lim f ( x) 0
x 0
2

3. Бесконечно малые, бесконечно большие функции Неопределенности

Повтор лекции 2
.
Бесконечно малые, бесконечно большие функции
Неопределенности
3

4. .

Два замечательных предела
Рассмотренные свойства функций, имеющих предел в точке a
расширенной числовой прямой, дают возможность
проанализировать их поведение в окрестности этой точки a .
Однако в ряде случаев этих свойств и установленных правил
предельного перехода недостаточно. Одним из классических
примеров подобного случая является поведение функции
(sin x) / x в окрестности точки a = 0 .
Пусть х - центральный угол окружности единичного радиуса ,
причем 0 < x < /2 (см. следующий слайд).

5.

/2.
Первый замечательный предел :
пусть х - центральный угол единичного круга, 0 < x <

6.

Повтор лекции 2
.
1
При этом xn xn 1 , т.е. последовательность {xn } 1
n
возрастает и она ограничена :
xn 2
1
1
1
2 ... n 1 2
1
2 2
2
1 (1 1 )
2
2n 1
1 12
следовательно 2 xn 3 , n
3
n
1
2 n. 1
6

7.

Повтор лекции 2
7

8.

Повтор лекции 2
8

9.

Сравнение функций при
*

10.

.

11.

Определение
Пусть f(x) и g(x) определены в Ú(a) .
f ( x)
1 , то функции f(x) и g(x) называются эквивалентными
g ( x)
Если x a
(асимптотически равными) при х → a . Обозначение: f ~ g , х → a .
lim
Пример : sin x ~ x , х → 0 .
Теорема (критерий эквивалентности функций)

12.

Повтор лекции 2
12

13.

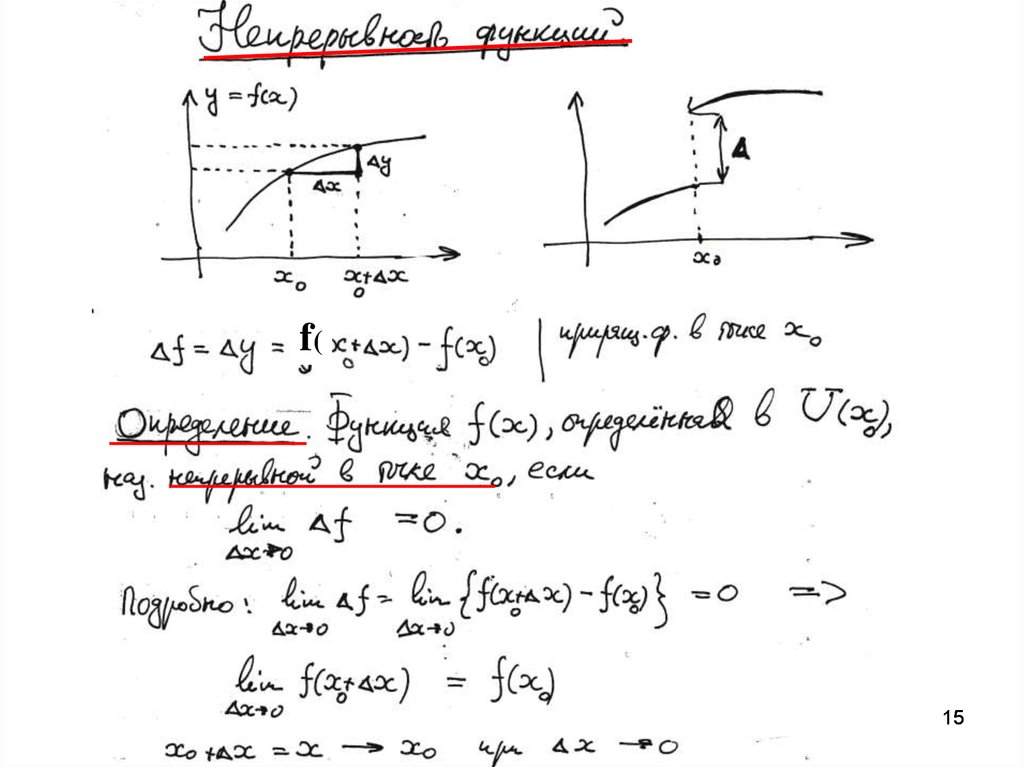
14. Непрерывные функции

.
14

15.

f(
15

16.

.
→
16

17.

.
17

18.

18

19.

.
10
19

20.

.
10
20

21.

.
21

22.

точке
22

23.

точке
23

24. Свойства функций, непрерывных в точке

Если функция f(x) непрерывна в точке α , то она имеет
конечный предел в ней, ограничена в окрестности т. α и при
условии f(x) ≠ 0 знакопостоянна. Из правил предельного перехода
при арифметических операциях следуют свойства непрерывности:
24

25. Продолжение

.
25

26.

1
5
2
3
4

27. Практические приемы

27

28.

28

29.

.
29

30. .

.
30

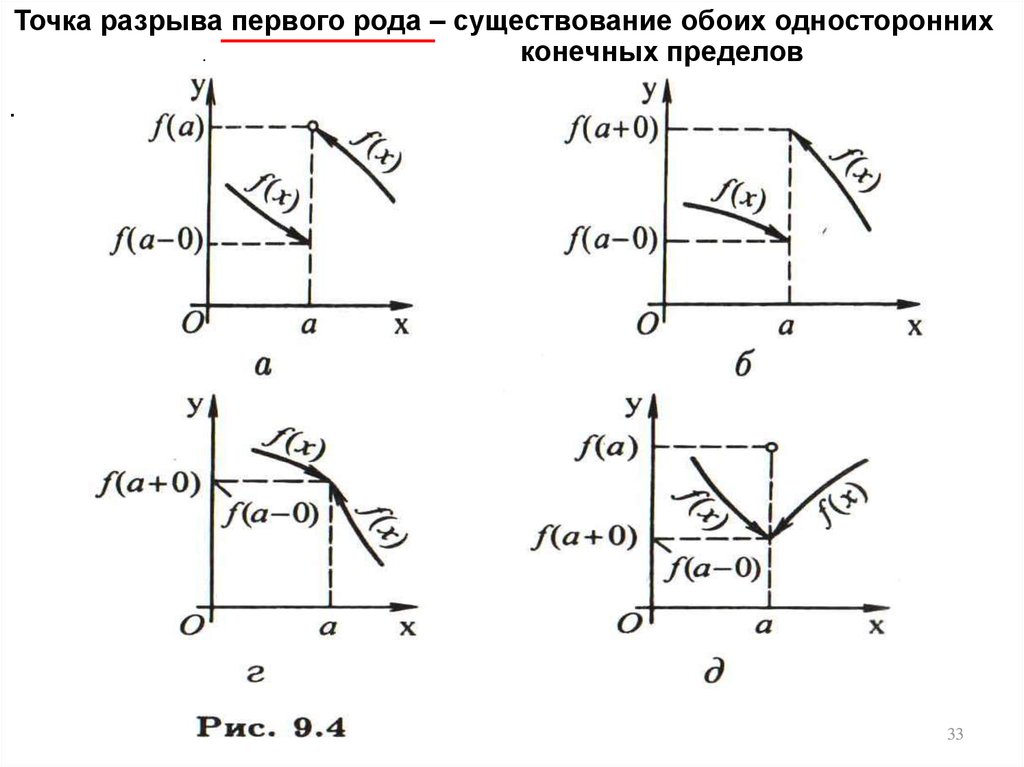
31. Точка разрыва первого рода – существование обоих односторонних конечных пределов

Рис. 9.4
31

32. Продолжение.

Если
32

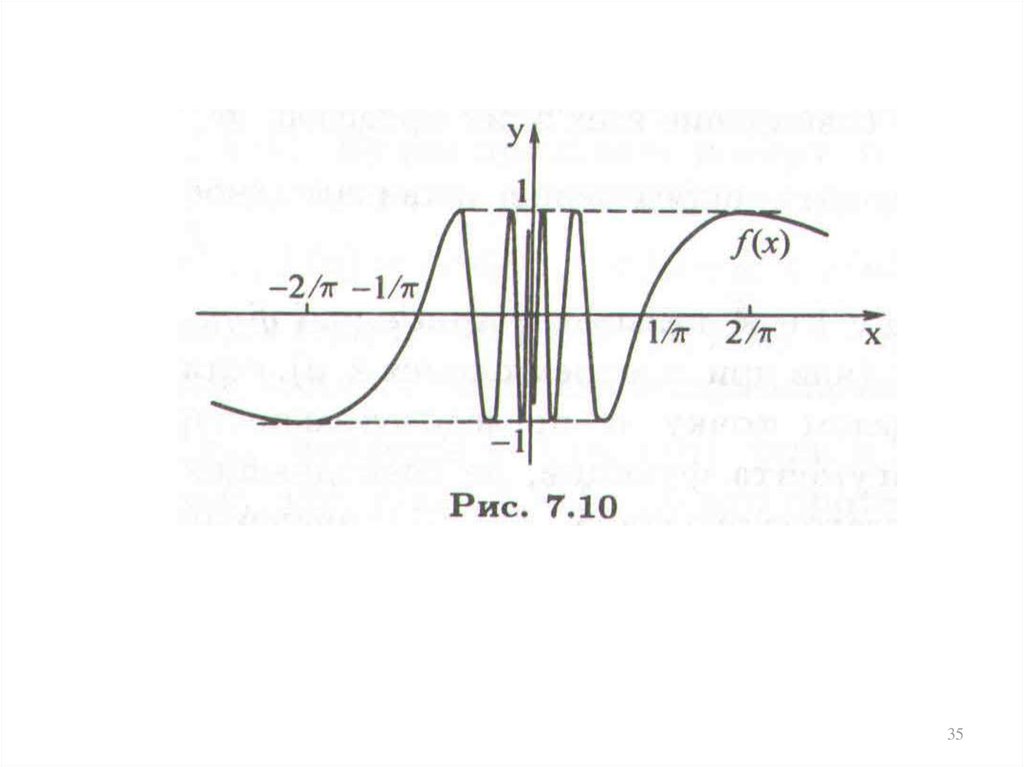
33. Точка разрыва первого рода – существование обоих односторонних . конечных пределов

.
33

34.

34

35.

35

36. Свойства непрерывных функций

Рис. 9.6
36

37. Теорема о промежуточном значении непрерывной функции

37

38. .

38

39. .

39

40.

40

41.

41

42.

42

43.

43

44. .

44

45.

45