Похожие презентации:
Нормированные пространства и Л.Н.О. Функциональный анализ
1.
Функциональный анализ2.
Нормированноепространство, Х – это
упорядоченная пара <X, . >,
где . - норма в л.п. Х
Норма, . - это функция . : X [0, + )
x,y X, R (C)
1 x = 0 x =
2 x = x
3 x + y x + y
3.
1.X=B[a, b] ( X=C[a, b])x X : x sup | x(t ) |
t [ a , b ]
2. X=L1[a, b]
b
x X : x 1 | x(t ) | dt
a
X L p [a, b], p 1
3. X=L2[a, b]
x X : x 2
b
a
| x(t ) | dt
4. X=l1
x X : x | xk |
k 1
2
x
| x(t ) | p dt
a
b
p
1
p
4.
5. X=l2.x X : x
2
|
x
|
k
k 1
6. X=Rn; Cn.
n
2
|
x
|
k
x X : x 2
k 1
x 1 | xk |
k 1
|| x ||sup sup | xk |
7. Х- л.п. ограниченных
последовательностей
k 1, n
x X : x sup | xk |
k 1,
5.
1) X C[0,1]x0 (t ) 2t 2 t 6
x0 ? Решение : x0 sup | 2t 2 t 6 | 6
t [ 0 ,1]
2) X C 3 [0,1]
x0 (t ) 2t 2 t 6
x0 ?
Решение : х0 sup | x0 (t ) | sup | x0 ' (t ) | sup | x0 ' ' (t ) | sup | x0 (t ) |
( 3)
[ 0 ,1]
[ 0 ,1]
[ 0 ,1]
[ 0 ,1]
6 5 4 0 15
3) X L2 [0, ], x0 (t ) t cos t
x0
3
6
0
1 2
1 2
3 1
| t cos t | dt
t dt t cos 2t dt
t sin 2tdt
0
0
2
2
6 2 0
4
2
6.
(2i )4) X l1 ; x0 n 1
3
n 1
n 1
n 1
1
2
2
x0 | xk | n 1 1
3
n 1
n 1 3
n
2 1
3
n 1 3
n
n 1
5) X l мн. огранич. послед тей; x0 {( i ) }
x0 sup | xn | sup 1n 1
n 1,
n 1,
7.
Метрика в н.п.Х – неотрицательнаяфункция d(x,y) = x - y : X X [0, + )
x,y,z X
1 d(x,y) = 0 x = y
2 d(x,y) = d(y,x)
3 d(x,y) d(x,z) + d(z,y)
Последовательность
х
n n 1
X , х0 Х
Определение. Последовательность {xn}
называется сходящейся к х0: xn x0 , если
d(xn , x) 0 , n ∞ xn x0 0, n
8.
Cходится ли xn n 1 к x0(t) 0 в н.п. X ?n
1. X=C[0,1], xn n 1 t n 1 t n 0 sup[0|,1t]n | 1 0, n
не сходится
2. X=C[0; 0,7], xn n 1 t n n 1
сходится
3. X=l1; x :
сходится
n n 1
nt
x
(
t
)
e
4. X=L2[0,+∞); n
сходится
e
nt
0
2
0
|e
nt
0 | dt
2
1
1
0, n
2n
2n
0
e 2 nt dt
9.
ОПРЕДЕЛЕНИЕПоследовательность {xn }
называется фундаментальной, если при
n,m d(xn , xm ) 0
Полным пространством называется м.п., в
котором фундаментальная
последовательность сходится
(к некоторому x0 X)
Полное нормированное пространство
называется банаховым
10.
11.
1f ( x) | f ( x) | dx, x C[ 1;1]
1
Покажем, что такое н.п. не является полным :
рассмотрим последовательность :
12.
13.
1) Согласованность линейной иметрической структуры в н.п.
1.1.Алгебраические операции в н.п.
непрерывны:
если (xn x, yn y, n )
а) xn + yn x + y
б) nxn x.
1.2. Норма непрерывна: xn x xn x .
1.3. Шар Bx0,R = x0 + R*B ,1.
Bx0 , R x X : x x0 R открытый шар
B x0 , R x X : x x0 R замкнутый шар
___
14.
если (p,q > 1 & 1/p + 1/q = 1 p + q = pqp = (p-1)q) тогда:
1) xy 1 x p y q.
2) (p 1) x + y p x p + y p.
15.
<X, . Х> банахово (1)(X - замкнутое п/п в б.п. <Y, . X>) (2)
( абсолютно сходящийся ряд в Х сходится)
(3)
Доказательство:
16.
17.
18.
19.
Теорема.<B(T), . sup> - банахово пространство.
Доказатель ство :
X B T множество функций , ограниченных на компакте Т
x B(T ) sup | x(t ) | ; || x ||sup sup | x(t ) |
t T
t T
Рассмотрим фундаментальную последовательность {xn (t )} n 1 X :
|| xn xm || 0, n, m ;
Фикс. t0 T : числовая последовательность {xn (t0 )} n 1 фундам. послед.
т.к. R банахово пр во, то {xn (t0 )}сходится : xn (t0 ) a0 , | a0 | .
Тогда , t0 T xn (t0 ) a0 , | a0 | . Следовательно,
последовательность{xn (t )} cххдится поточечно к х(t ) : xn (t ) x(t ), t T ;
где x(t ) a0 , t t0 T ; | x(t ) | sup | a0 | x(t ) B (T );
t 0 T
Докажем сходимость по норме :
t T : | xn (t ) x(t ) | sup | xn (t ) x(t ) | | xn (t0 ) a0 | 0, n
t T
переходя к sup по t T , получим :
|| xn x || 0, n .
Таким образом, фундам. посл ть сходится В(Т ) банахово пр во.
20.
1) l - б.п.;2) если T – компактное множество
<С(T), . sup> - б.п.;
3) C[a, b] – сепарабельное (в нем существует
счетное, всюду плотное множество),
бесконечномерное б.п.
21.
Лемма Рисса о почти перпендикуляре.(Пусть X н.п., X Y-замкнутое п/п в Х, >0),
тогда ( p X p = 1 & dist(p,Y) 1- ).
Определение. Множество D X является
ограниченным, если содержится в шаре
конечного радиуса:
R 0 : D Bx0 , R
x D : x x0 R
22.
1) X C[0,1];D x X : x(t ) C1 C2t 2 , | C1 | 2; | C2 | 1 Sp (1, t 2 )
Проверим ограниченность :
x D : x x C1 C2t 2 | C1 | | C2 | t 2
( t 2 sup | t 2 | 1) | C1 | | C2 | 2 1 3
[ 0 ,1]
x B ,3 D B ,3 D ограничено в Х
2) X L1[0,1]; D x X :| x(t ) | 2
1
1
0
0
x D : x 1 x 1 | x(t ) | dt 2 dt 2
x B , 2 D B , 2 D ограничено в Х
23.
24.
25.
Пусть X,Y-н.п.А: Х→Y – линейный операторОпределение. Оператор А называется
ограниченным, если он всякое
ограниченное множество переводит в
ограниченное: D B , r A( D) B , R
X
Y
Определение.
Оператор А называется непрерывным,
если
( xn : xn x0 , n ) ( A( xn ) A( x0 ), n )
26.
1) X Y C[0,1];( Ax)(t ) a (t ) x(t ), t [0,1]
a (t ) C[0,1]
2) X Y L1[0,1]
1
( Ax)(t ) k (t , s) x( s) ds, k (t , s) L1[0,1]2
0
3) X Y C ( ; )
( Ax)(t ) x(t h), h R
4) X Y l2 ;
Ax (0, 0, x1 , x2 , ...., xn , ...)
27.
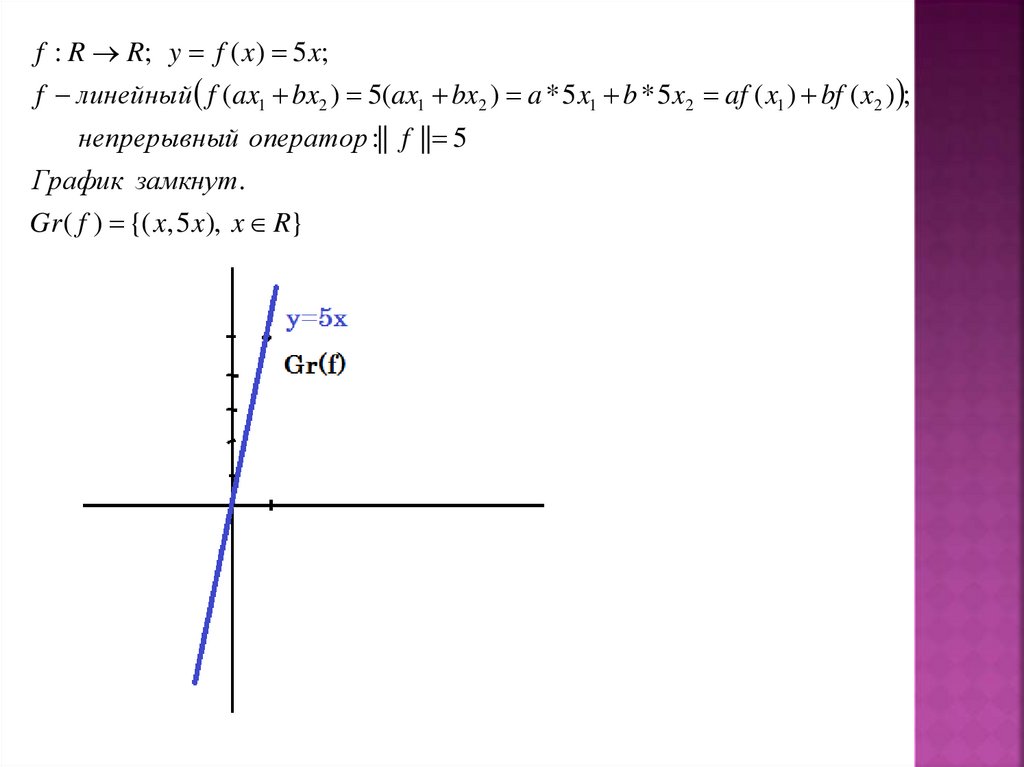
Пусть A:<X, . Х> <Y, . Y> - л.о., тогда(1)
(2)
(A непрерывен) (A непрерывен в т. )
(3)
(4)
(А ограничен) ( M 0 : Ax M x , x X )
Доказательство:
1 ? 1 ? - Очевидно!
2 1 ? xn x =(непрерывность
алгебраических операций в Х) xn - x X
=(2 ) A(xn - x) A X =





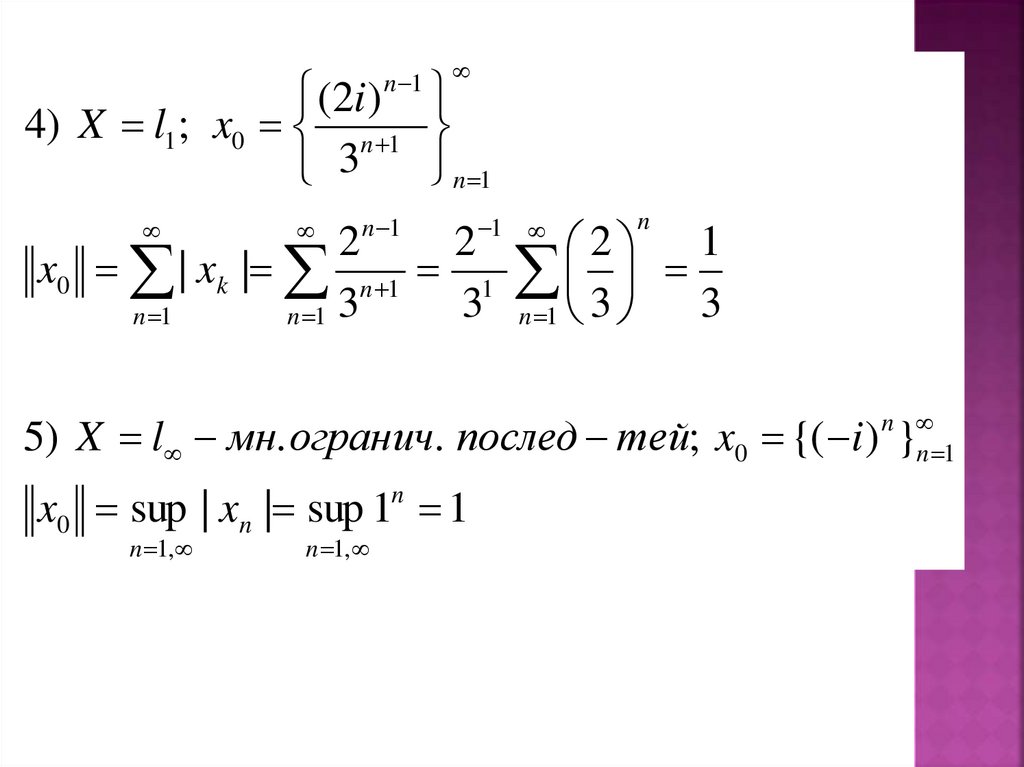



































 Математика
Математика








