Похожие презентации:
Разложение вектора по направлениям. Скалярное произведение векторов
1.
2.
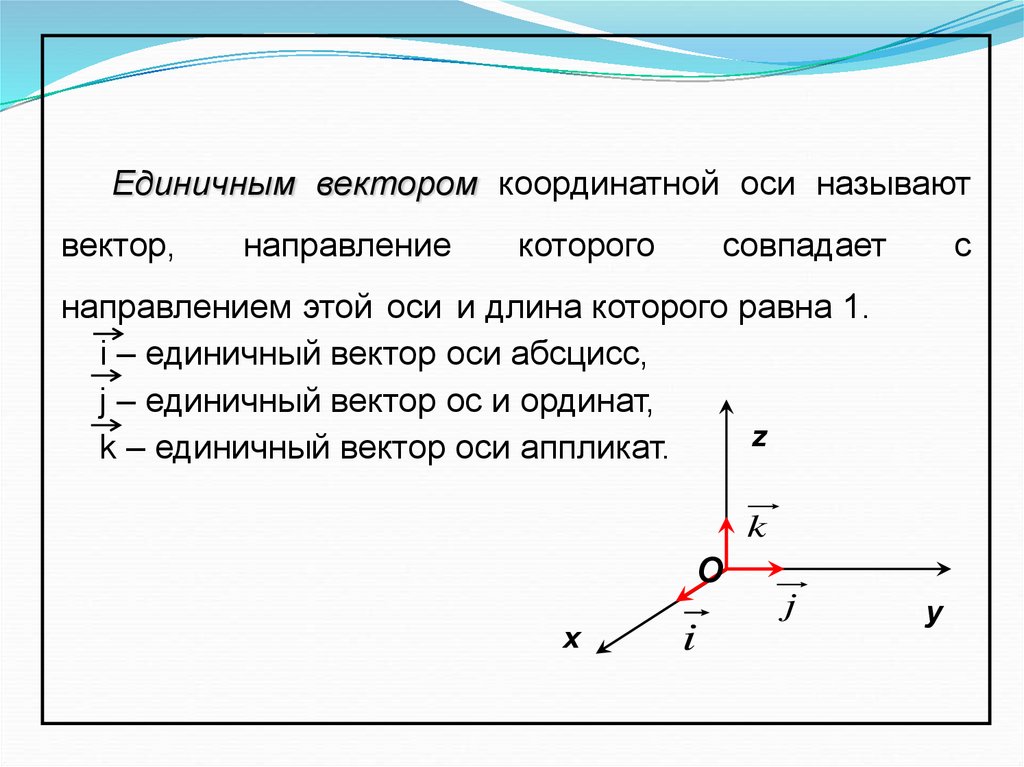
Единичным вектором координатной оси называютвектор,
направление
которого
совпадает
с
направлением этой оси и длина которого равна 1.
i – единичный вектор оси абсцисс,
j – единичный вектор ос и ординат,
z
k – единичный вектор оси аппликат.
k
O
j
x
i
y
3.
Любой вектор можно разложитьвекторам, т.е. представить в виде:
по
координатным
Нулевой вектор также можно представить в таком виде:
Координаты равных векторов соответственно равны:
Сумма (разность) векторов:
Произведение вектора на число:
4.
Вектор, конец которого совпадает с данной точкой, аначало – с началом координат, называется радиус-вектором
данной
точки.
Координаты
любой
точки
равны
соответствующим координатам её радиус-вектора.
5.
Координаты середины отрезкаДлина вектора по его координатам:
6.
Даны векторы:Найти вектор, равный:
Найдите значения m и n, при которых векторы
коллинеарны.
7.
АУгол между векторами
а
О
Если
Если
Если
α
В
b
и
,то
и
, то.
, то
8.
d c= 180
0
a
f
d
c
d f
= 0
0
b
a b
a c
b c
= 30
0
= 120
= 90
0
0
9.
Скалярным произведением двух векторов называетсяпроизведение их длин на косинус угла между ними.
a
b
=
a
b cos( a b)
Скалярное произведение векторов – число (скаляр).
Если векторы перпендикулярны, то скалярное произведение
этих векторов равно нулю.
0
a b = 90
b
a
10.
a b < 90b
0
a
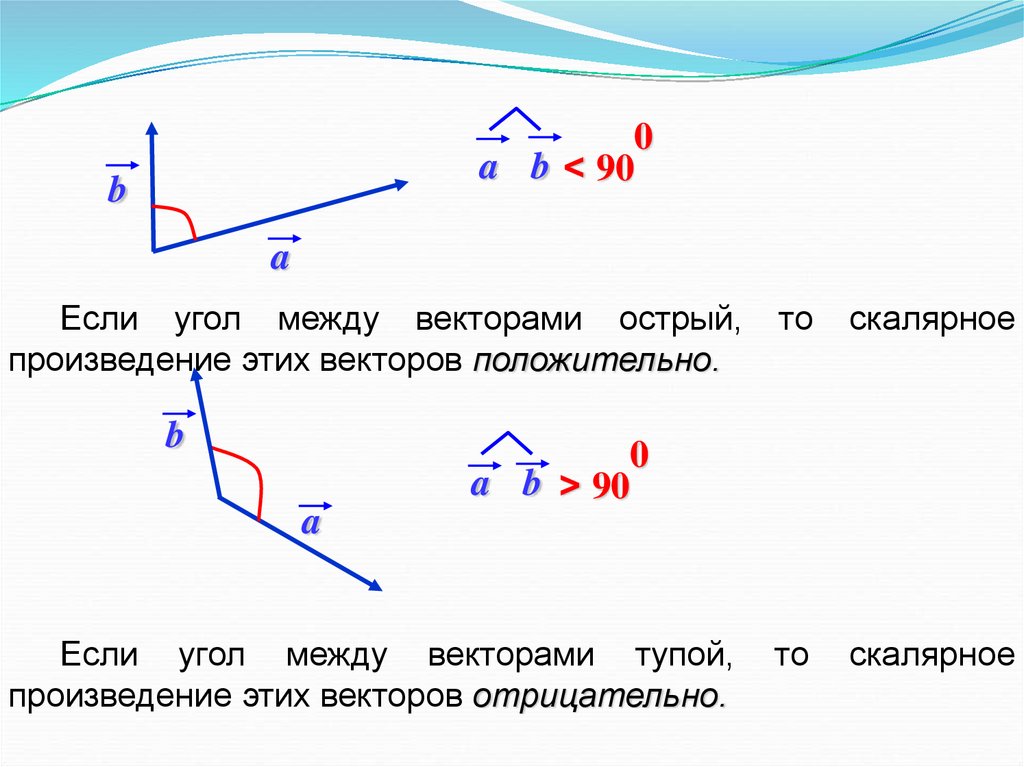
Если угол между векторами острый,
произведение этих векторов положительно.
b
a b > 90
то
скалярное
то
скалярное
0
a
Если угол между векторами тупой,
произведение этих векторов отрицательно.
11.
a b=
a
b сos (a b )
Пусть векторы заданы своими координатами a ( x1; y1; z1 )
и b ( x2; y2; z2 ). Тогда скалярное произведение этих векторов
равно
2
a · b = x1x2 + y1y2 + z1z2
2
a = |a|
cos
x1 x2 y1 y2 z1 z 2
x12 y12 z12 x22 y22 z 22
cos
a b
| a | | b |









 Математика
Математика








